Урок по теме «Упрощение выражений», 5 класс

Урок по теме «Упрощение выражений», 5 класс

Цели урока: познакомить учащихся с распределительным свойством умножения относительно сложения и относительно вычитания; учить применять это свойство при устных вычислениях.

Ход урока

I. Организационный момент

II. Устный счет. Определение темы урока

На доске:

— Найдите значения выражений.

— Какие свойства вам пришлось использовать при вычислениях?

— Расскажите, как вы вычисляли сумму 56 ∙ 4. (56 ∙ 4 = (50 + 6) ∙ 4 = 50 ∙ 4 + 6 ∙ 4 = 224.)

— Сформулируйте это правило.

Сегодня на уроке мы повторим правила, которые вы изучали в начальной школе, дадим им новое название и будем учиться применять их при упрощении выражений.

III. Повторение правил умножения суммы на число и умножения разности на число

На доске:

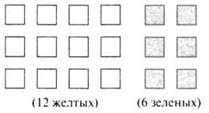
— Что вы видите на доске?

— Как найти сумму всех квадратов?

(4 + 2) ∙ 3 = 6 ∙ 3 = 18. (Сначала узнаем, сколько квадратов в одном ряду, затем, умножив на 3, узнаем, сколько всего квадратов.)

— Как можно вычислить количество другим способом?

4 ∙ 3 + 2 ∙ 3 = 12 + 6 = 18. (Сначала узнаем, сколько желтых квадратов, потом — сколько зеленых. Сложив полученные произведения, найдем, сколько всего квадратов.)

— Что мы находили первым выражением? Что находили вторым выражением? Какой знак можно поставить между ними?

(4 + 2) ∙ 3 = 4 ∙ 3 + 2 ∙ 3

— Как называется это правило?

— Сформулируйте правило умножения суммы на число.

— Как узнать, на сколько желтых квадратов больше, чем зеленых?

(4 — 2) ∙ 3 = 4 ∙ 3 — 2 ∙ 3 = 6. (Узнаем, на сколько желтых больше, чем зеленых, в одном ряду. Умножив на 3, узнаем, на сколько желтых больше, чем зеленых.)

— Как можно вычислить по-другому?

4 ∙ 3 — 2 ∙ 3 = 6. (Узнаем, сколько всего желтых квадратов и сколько всего зеленых. Вычтем из первого произведения второе и узнаем, на сколько желтых квадратов больше, чем зеленых.)

— Дайте название этому правилу.

— Сформулируйте правило умножения разности на число.

IV. Работа по учебнику

1. Работа по статье учебника.

— Прочитайте статью учебника и приготовьтесь отвечать на вопросы.

— Сформулируйте распределительное свойство умножения относительно сложения.

— Сформулируйте свойство умножения относительно вычитания.

— Объясните, для чего мы изучаем распределительное свойство умножения.

— Запишите распределительное свойство умножения относительно сложения и относительно вычитания при помощи букв.

(Учащиеся записывают эти свойства на доске, учитель выставляет карточки.)

(а + b) ∙ с = ас + bс

(а — b) ∙ с = ас — bс

— Проговорите распределительное свойство, глядя на карточки.

2.— Прочитайте задание. Рассмотрите образец.

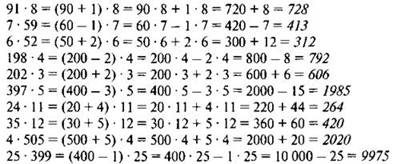
— Какое свойство мы использовали для вычислений?

— Сформулируйте.

ФИЗМИНУТКА

3. Прочитайте задание.

Распределительное свойство умножения нужно уметь видеть и узнавать и по второй части записи.

69 ∙ 27 + 31 ∙ 27 =

— Какой множитель повторяется?

— Какой знак стоит между произведениями?

— Как “собрать” запись?

(Далее задание выполняется в паре.)

Проверка

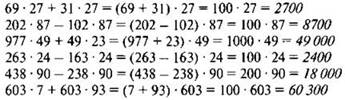
VI. Повторение изученного материал (работа в паре с последующей проверкой).

VII. Рефлексия

— Какое новое знание получили на уроке?

— Сформулируйте распределительное свойство умножения относительно сложения, относительно вычитания.

Итоги урока. Выставление оценок за урок.

Домашнее задание.