Конспект урока математики в 9 классе по теме: «Практическое применение теоремы синусов и косинусов»

Тема урока: «Практическое применение теоремы синусов и косинусов»

Тип урока: «Урок практикум»

Цели урока:

Образовательные (формирование познавательных УУД): – обобщить и закрепить имеющиеся знания по теме, продемонстрировать прикладной характер геометрии;

Развивающие (формирование регулятивных УУД): – способствовать развитию познавательных и исследовательских умений учащихся, использовать для достижения поставленной задачи уже полученных знаний, организация поисковой деятельности;

Воспитательные (формирование коммуникативных и личностных УУД): – воспитание ответственности за свою работу и труд одноклассников, повышать культуру общения, умение сотрудничать, выступать и отстаивать свои суждения.

План урока

Начало урока

I.                   Актуализация знаний;

II.                Работа в группах.

III.             Подведение итогов. Рефлексия.

IV.            Домашнее задание.

Ход урока

I.                  Вступительное слово учителя

На предыдущих уроках мы познакомились с важными теоремами геометрии – теоремой синусов и теоремой косинусов, научились применять их при решении треугольников. Очень часто, изучая геометрию, вы задаете себе вопрос: «А зачем это нужно?». Вот сегодня мы вместе и попытаемся ответить на вопрос: «А зачем нужны теоремы синусов и косинусов?».

Обучающи ся  ставят  задачи и цели урока. Актуализация знаний

1.     Фронтальный опрос: вопросы опроса

-       что значит решить треугольник?

-       по каким элементам можно решить треугольник?

-       какие теоремы позволяют решить эту задачу?

-       сформулируйте теорему синусов, теорему косинусов, теорему о сумме углов треугольника;

-       чему    равно    отношение    стороны    треугольника    к    синусу противолежащего угла?

-       как еще называют теорему косинусов? Почему?

-       как определить вид треугольника с помощью теоремы косинусов?

2.     Проверка решений задач по готовым чертежам ( 2 ученика решали их на доске во время фронтального опроса).

3.      Найти сторону

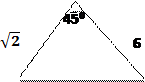
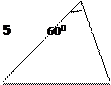3

4

х                                                                         х

8

х =  =                            х =                                          №1

х =  =                     х =                                           №2

х =                                                 =            х =                                            №3

4.     Историческая справка.

Выступление одного ученика с сообщением о развитии тригонометрии.

II.      Работа в группах.

1   группа. Применение теоремы синусов и косинусов в планиметрии для получения новых фактов, формул.

Задача №1. Доказать, что в любом треугольнике

a, b, c – стороны треугольника S – площадь треугольника

S = abc , где

4R

R – радиус окружности, описанной около треугольника.

Задача №2. Докажите, что биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.

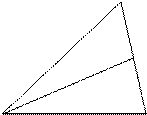B                          L - биссектриса

с              a_c                        Доказать, что

ac = ab

c      b

a_b

A                b            C

Задача №3. Докажите, что в параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон.

Задача №4. Стороны треугольника a, b, c. Докажите, что если a²+b²>c², то угол противолежащий стороне с острый, если a²+b²<c², то этот угол – тупой.

2   группа. Применение теоремы синусов и косинусов для решения задач по физике.

Задача №1. Силу, равную 23 Н, требуется разложить на две составляющие, углы которых с направлением заданной силы равны 47⁰ и 54⁰. Найти величину каждой из этих сил.

Задача №2. Сила Р = 240 Н разложена на две составляющие Р₁ = 185 Н и Р₂ = 165 Н. Под каким углом действуют силы Р₁ и Р₂?

Задача №3. Железный стержень длиной, а требуется изогнуть под прямым углом так, чтобы расстояние между концами было равно b. Где должна находиться точка сгиба? При каких условиях задача имеет решение?

3      группа. Применение теоремы синусов и косинусов в задачах с практическим содержанием.

Задача №1. Две планки длиной 35 см и 42 см скреплены одним концом. Какой взять угол между ними, чтобы расстояние между другими концами планок равнялись 24 см.

Задача №2. Спортивный самолет летит по замкнутому треугольному маршруту. Два угла этого треугольника 60⁰ и 100⁰. Меньшую сторону он пролетел за 1 ч. За сколько времени он пролетит весь маршрут, сохраняя постоянную скорость.

Задача №3. На крышке парового цилиндра диаметром 350 мм требуется просверлить 8 отверстий для болтов. Найдите расстояние между центрами отверстий, если эти центры должны отстоять от краев крышки на 50 мм.

Задача №4. С вертолета, находящегося над шоссейной дорогой, была замечена двигавшаяся по ней колонна машин. Начало колонны видно под углом понижения 75⁰, а конец – под углом 70⁰. Найдите длину колонны, если вертолет находится на высоте 1650 м.

III.           Подведение итогов. Рефлексия.

IV.            Домашнее задание

Задания  на учи.ру  практикум-уникум.