
Урок - смотр знаний по теме
«Соотношения между сторонами и углами треугольника»
9 класс
Тип урока: урок обобщения изученного материала, применения теоретических знаний при решении задач.
Цели урока:
· Образовательные: систематизировать, обобщить, проверить и оценить знания учащихся по изученной теме; формировать умения и навыки применения теоретических знаний при решении задач.
· Развивающие: учить проводить доказательные рассуждения, используя математическую речь; учить умению сосредотачиваться на учебной деятельности и предупреждать ошибки по невнимательности (развивать самоконтроль), формировать коммуникативные навыки и волевые качества личности.
· Воспитательные: развитие любознательности учащихся, познавательного интереса к математике; развивать творчество учеников.
Методы, используемые на уроке: частично-поисковые.
Оборудование: ноутбук, проектор, экран, презентация, карточки с заданиями для команд.
Ход урока
1. Организационный момент
Класс разбивается на 3 команды. Каждая команда выбирает капитана, придумывает название команды, девиз. За каждый вид деятельности учащиеся получают не оценки, а баллы. В конце смотра по сумме набранных баллов выставляется оценка в журнал. Если ученик заработал 15 баллов и больше – ему выставляется оценка «5», от12 до 15 баллов – оценка «4», от 9 до 12 баллов – оценка «3», меньше 9 баллов – оценка «2».
Итак, общественный смотр знаний – праздник для учащихся и учителя.
2. Словарный диктант (20 слов)
Если ученик не сделал ошибок – ему выставляется 5 баллов, 1 ошибка – 4 балла, 2 ошибки – 3 балла, 3 ошибки – 2 балла, 4 ошибки – 1 балл, 5 и более ошибок – 0 баллов.
|
Планиметрия, геометрия, аксиома, треугольник, принадлежащая, пересекаются, прямая, плоскость, теорема, лемма, существует, единственная, следовательно, косинус, доказательство, параллельные, расстояние, тригонометрия, перпендикулярная, математика |
3. «Истина – ложь»
( на предложенные высказывания учащиеся Или работа с карточками на интерактивной панели показывают ту карточку с буквой которую считают верной «И» - истина, «Л» - ложь)
1) Треугольник это геометрическая фигура имеющая 3 стороны и 3 угла И
2) Каждая сторона треугольника равна сумме двух других сторон Л
3) В треугольнике против меньшего угла лежит большая сторона Л
4) Площадь треугольника равна произведению его стороны на высоту проведенную к этой стороне И
5) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без произведения этих сторон на косинус угла между ними Л
6)  Верно ли выражение
для данного треугольника
Верно ли выражение
для данного треугольника
![]() Л
Л
7) Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе И
8) ![]() И
И
9) ![]() И
И
10) Решить треугольник значит найти угол и сторону этого треугольника. Л
3. Программированный контроль
0 ошибок – 5 баллов, 1 ошибка – 4 балла, 2 ошибки – 3 балла, 3 ошибки – 2 балла, 4 ошибки – 1 балл, 5 ошибок – 0 баллов.
Отметьте в карточке правильный ответ знаком «Х».
Задание для первой команды
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание для второй команды
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание третьей команды
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы:
Задание для первой команды
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
Х |
|
|
|
|
Задание для второй команды
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
Задание третьей команды
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
4. Физкультминутка
5. Задача с практическим содержанием
|
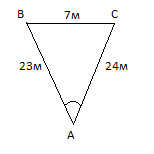
Футбольный мяч находится в точке А футбольного поля на расстояниях 23 м и 24 м от оснований В и стоек ворот. Футболист направляет мяч в ворота. Найдите угол α попадания мяча в ворота, если ширина ворот равна 7 м. |
Решение:
Решим треугольник АВС(задача 1) и найдем угол А, равный α
По теореме косинусов определим cos А
![]()
![]()
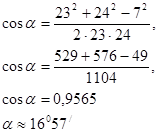
Ответ: 16057/
6-а. Тест (Google-формы) ссылка https://forms.gle/EfPWXFWEakFd8KxWA
Максимальное количество баллов - 10
|
1. Стороны треугольника 5 см и 3 см, а угол между ними 30⁰. Найдите площадь треугольника. а) 15 см2; б) 7,5 см2; в) 3,75 см2; г) 30 см2. 2.
Стороны параллелограмма равны а)
3. В треугольнике АВС АВ = 5 см, АС = 12 см, угол С равен 30⁰. Найдите угол В. а)
90⁰; б) 4. По теореме синусов: а) Стороны треугольника обратно пропорциональны синусам противоположных углов. б) Стороны треугольника пропорциональны синусам противоположных углов. в) Стороны треугольника пропорциональны синусам прилежащих углов. 5. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то эта сторона лежит против: а) тупого угла; б) прямого угла; в) острого угла. 6. По теореме о площади треугольника: а) Площадь треугольника равна произведению двух его сторон на синус угла между ними. б) Площадь треугольника равна половине произведения двух его сторон на угол между ними. в) Площадь треугольника равна половине произведения двух его сторон на синус угла между ними |
6-б. Готовимся к ГИА.
Задача 1.
В треугольнике ABC АD-
биссектриса, ![]() С=103°,
С=103°,
![]() CAD=4°.
CAD=4°.
Найдите ![]() В.
В.
 Решение.
Решение.
Так как AD
– биссектриса ![]() А,
то
А,
то ![]() А=8°,
тогда
А=8°,
тогда ![]() В=180°-(103°+8°)=69°.
В=180°-(103°+8°)=69°.
Задача 2.
Один из острых углов прямоугольного треугольника в два раза больше другого.
Найти меньший острый угол.
Решение.
Сумма острых углов прямоугольного треугольника равна 90°, 90° : 3=30°.
Ответ: 30°.
Задача 3. Один из углов прямоугольного треугольника равен 60°, сумма гипотенузы и меньшего катета равна 42 см. Найти гипотенузу.
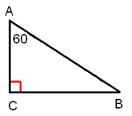 Решение.
Решение.
![]() В=30°
, АВ+АС=42; АВ+
В=30°
, АВ+АС=42; АВ+![]() АВ=42; 1
АВ=42; 1![]() АВ=42; АВ=42
АВ=42; АВ=42![]()
![]() =28 см.
=28 см.
Ответ: 28 см.
(дополнительно при наличии времени)
САМОСТОЯТЕЛЬНАЯ РАБОТА.
I вариант
1.
Площадь
параллелограмма равна 30![]() см2, а один
из углов равен 600. Найдите его периметр, если длина одной из
сторон равен 6 см.
см2, а один
из углов равен 600. Найдите его периметр, если длина одной из
сторон равен 6 см.
2.
В
треугольнике MNK MN
= NK, MK
= ![]() , ∟M
= 300, MA – биссектриса. Найдите
МА.
, ∟M
= 300, MA – биссектриса. Найдите
МА.
3. Стороны треугольника равны 8, 10 и 12 см. Найдите угол, лежащий против меньшей стороны.
II вариант
1.
Площадь
параллелограмма равна 40![]() см2, а один
из углов равен 450. Найдите его периметр, если длина одной из
сторон равен 10 см.
см2, а один
из углов равен 450. Найдите его периметр, если длина одной из
сторон равен 10 см.
2.
В
треугольнике CDE CM
– биссектриса, ∟DCE
= 600, ME
= ![]() . Найдите CМ,
если ∟CED = 450.
. Найдите CМ,
если ∟CED = 450.
3. Стороны треугольника равны 6, 9 и 10 см. Найдите угол, лежащий против большей стороны.
Ответы к задачам самостоятельной работы:
|
Вариант |
1 |
2 |
3 |
|
I |
10 см |
1 см |
41030| |
|
II |
8 см |
6 см |
80057| |
6. Рефлексия
Было ли вам
интересно на уроке?
Какие вопросы сегодня на уроке вызвали у вас трудности?
Удалось ли их преодолеть?
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.