
Розділ 2
ВНУТРІШНЬОАПАРАТНА ГІДРОМЕХАНІКА
2.1. Основи технічної гідравліки.
2.1.1. Загальні відомості про гідравліку.
У хімічній технології процеси переносу найбільш часто протікають у рідинній, газовій чи паровій фазах при їхньому русі і перемішуванні. При цьому швидкість процесів переносу в значній мірі залежить від гідродинамічних умов у технологічних апаратах. У багатьох випадках гідродинамічні умови можна спрямовано регулювати з метою створення в апаратах оптимальних режимів здійснення процесів.
Технічна гідравліка – це наука, що вивчає закони рівноваги і руху різних рідин і газів в елементах машин і апаратів.
Гідравліку підрозділяють на гідростатику, у якій розглядаються закони рівноваги рідин у стані спокою, і гідродинаміку (закони руху рідин). При цьому в понятті рідини прийнято поєднувати власне рідини, а також гази і пари, оскільки при швидкостях потоків, значно менших, ніж швидкість звуку, закони руху рідин без істотних виправлень справедливі для газів і парів. Таким чином, у гідравліці під рідинами прийнято розуміти всі речовини, що володіють текучістю.
При виведенні основних законів у гідравліці вводять поняття ідеальної рідини, під якою (на відміну від реальної рідини) мають на увазі рідину, абсолютно не стискувану, що не змінює своєї густини під дією температури і тиску і не володіє в'язкістю.
Реальні рідини підрозділяють на краплинні і пружні (гази і пари). Краплинні рідини можна вважати практично нестисливими, вони мають відносно малий коефіцієнт об'ємного розширення. Пружні рідини навпаки суттєво змінюються при зміні температури і тиску (гази та пари).
2.1.2. Сили, що діють у реальній рідині.
Рідина в стані спокою чи руху знаходиться під впливом різних сил, які можна розділити на об'ємні і поверхневі.
Об'ємні сили діють на кожен елемент даного об'єму рідини і пропорційні масі, що знаходиться в даному об'ємі. До них відносяться сили ваги (G=m×g), сили інерції (Fi=m×a) і відцентрові сили (Fв.ц=mw2/R).
Характеристикою інтенсивності сили ваги
![]() , що діє на даний об’єм
, що діє на даний об’єм ![]() , є питома вага рідини:
, є питома вага рідини:
![]() (2.1)
(2.1)
Границя відношення маси рідини до об'єму при його стягуванні в точку називають густиною рідини:
![]() (2.2)
(2.2)
Питома вага і густина краплинних рідин мало залежать від тиску і температури, їх звичайно визначають експериментально. Густина газів при порівняно низьких тисках може бути розрахована за рівнянням стану ідеальних газів:
![]() (2.3)
(2.3)
де R = 8310 Дж/(кмоль∙К) - універсальна газова стала, P, T і M - відповідно тиск, температура і молекулярна маса газу.
При підвищених тисках густина газів може бути розрахована з урахуванням коефіцієнта стискальності Z, що визначається як функція (представляється звичайно графічною залежністю) від приведених температури Tпр і тиску Рпр:
![]() (2.4)
(2.4)
Поверхневі сили діють на поверхні, що обмежує даний об'єм рідини і відокремлює його від навколишнього середовища. До них відносяться сили тиску, сили внутрішнього тертя (сили в'язкості) і сили поверхневого натягу. Ці сили пропорційні розміру поверхні, на якій вони діють.
Характеристикою інтенсивності поверхневих сил є напруження t, яке створюється ними на поверхні S, що обмежує даний об'єм V:
![]() (2.5)
(2.5)
Параметром, що характеризує дію сил тиску рідини на дно та стінки об’єму, в якому вона знаходиться, а також на поверхню любого зануреного в неї тіла, є гідростатичний тиск. Якщо виділити всередині рідини, що знаходиться в стані спокою, елементарну площадку DS, то по нормалі до неї буде діяти сила тиску стовпа рідини DР . Співвідношення DР/DS представляє собою середній гідростатичний тиск, а границю цього відношення при DS®0 називають гідростатичним тиском в даній точці або просто гідростатичним тиском р:
p=limDS®0(DP/DS), [Н/м2=Па]. (2.6)
Тиск в любій точці рідини діє однаково по всіх напрямках і може бути виражений в одиницях стовпа рідини:
р=gH=rgH, (2.7)
де Н – висота стовпа рідини над даною точкою.
У зв’язку з цим можна встановити наступні співвідношення між різними діючими одиницями тиску: 1 атмосфера технічна (1 ат) = 735,6 мм рт. ст. = 10 м вод. ст. = 98 100 Н/м2(Па) » 0,1 МПа.
Прилади для вимірювання тиску (манометри та вакуумметри) показують не абсолютний тиск рабс всередині замкнутого об’єму, а різницю між абсолютним і атмосферним тиском ратм. Цю різницю називають надлишковим тиском рнад, якщо тиск в об’ємі вище атмосферного, або розрідженням ррозр, якщо воно нижче атмосферного (в системі вакуум). Таким чином, співвідношення між показаннями манометра рм або вакуумметра рв і абсолютним тиском в системі мають вигляд:
рабс= ратм+ рнад= ратм+ рм , (2.8)
рабс= ратм- ррозр= ратм- рв . (2.9)
При рівновазі рідини у стані спокою на неї діють сили ваги і сили тиску, у той час як закономірності руху реальних рідин визначаються дією не тільки цих сил, але й у дуже великій мірі силами внутрішнього тертя (силами в'язкості).
 В’язкість – це властивість рідини чинити опір зусиллям, що
викликають її деформацію. За рахунок в’язкості при русі рідини між сусідніми
шарами рідини виникають сили тертя. Дотичні напруження (2.5), що виникають під
дією сил тертя, називають напруженнями сил внутрішнього тертя або напруженнями
зсуву. Їхнє утворення викликане нерівномірністю епюри швидкості в потоці
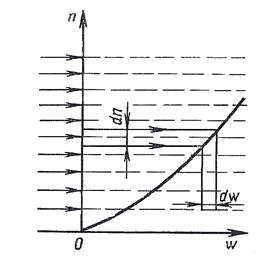
рідини (рис. 2.1).
В’язкість – це властивість рідини чинити опір зусиллям, що
викликають її деформацію. За рахунок в’язкості при русі рідини між сусідніми
шарами рідини виникають сили тертя. Дотичні напруження (2.5), що виникають під
дією сил тертя, називають напруженнями сил внутрішнього тертя або напруженнями
зсуву. Їхнє утворення викликане нерівномірністю епюри швидкості в потоці
рідини (рис. 2.1).
Рис.2.1. Профіль швидкості в поперечному перерізі прямолінійного потоку рідини.
Нерівномірність розподілу швидкості пояснюється взаємодією між сусідніми шарами рідини внаслідок взаємного обміну молекул, що хаотично рухаються, і взаємного притягнення молекул близько розташованих шарів рідини, а також взаємодією часток рідини з поверхнею каналу або рухомого тіла. Частки рідини, що прилягають до поверхні твердого тіла, «прилипають» до неї, і їхня швидкість відносно цього тіла дорівнює нулю. Таким чином, рухоме тверде тіло сприяє прискоренню найближчих шарів рідини, передаючи їм імпульс, а ті, в свою чергу, передають імпульс більш дальнім шарам, прискорюючи і їх. В рідині виникає градієнт швидкості dw/dn. Експериментально встановлено, що для багатьох рідин величина дотичних напружень сил тертя в даній точці елемента поверхні, розташованої між двома рухомими шарами рідини, пропорційна градієнту швидкості:
tт = - m × ( dw/dn), (2.10)
де знак «мінус» вказує на те, що нормаль до поверхні направлена в бік зменшення швидкості, інакше кажучи, напруження внутрішнього тертя, що виникає між шарами рідини при її русі, гальмує шар, що рухається з більшою швидкістю, або розганяє більш повільний шар.
Коефіцієнт пропорційності m (Па×с) в рівнянні (2.10), називають коефіцієнтом динамічної в’язкості або просто динамічною в’язкістю, яка є однією з основних фізичних характеристик рідин. Вона характеризує опір рідини зсуву окремих її шарів. В’язкість крапельних рідин, як правило, зменшується з підвищенням температури внаслідок збільшення відстані між молекулами та послаблення сил притягнення між ними. Навпаки, в’язкість пружних рідин зростає з підвищенням температури і тиску внаслідок інтенсифікації теплового руху і обміну імпульсами між шарами потоку. Величина m визначається дослідним шляхом і наводиться в довідковій літературі.
В інженерних розрахунках часто використовують поняття кінематичної в’язкості, яка виражає співвідношення динамічної в’язкості та густини рідини n =m /r, м2/с.
Сила тертя Fт між двома поруч розташованими шарами рідини з поверхнею розділу між ними S дорівнює
Fт = - m × ( dw/dn)× S (2.11)
 Рівняння (2.10, 2.11) виражають закон внутрішнього тертя
Ньютона. Він є справедливим для переважної кількості рідин з невеликою
молекулярною масою, в'язкість яких є функцією температури і тиску, але не
залежить від швидкості зсуву dw/dn. Такі
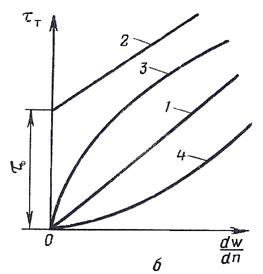
рідини називають нормальними або ньютонівськими. Залежність tт від dw/dn (крива течії) для них є лінійною (рис.
2.2, лінія 1).
Рівняння (2.10, 2.11) виражають закон внутрішнього тертя
Ньютона. Він є справедливим для переважної кількості рідин з невеликою
молекулярною масою, в'язкість яких є функцією температури і тиску, але не
залежить від швидкості зсуву dw/dn. Такі
рідини називають нормальними або ньютонівськими. Залежність tт від dw/dn (крива течії) для них є лінійною (рис.
2.2, лінія 1).
Рис.2.2. Залежність напруження внутрішнього тертя від швидкості зсуву: 1 – ньютонівські рідини, 2 – бінгамівські рідини, 3 – псевдопластичні рідини, 4 – ділатантні рідини.
Рідини, у яких в’язкість залежить від швидкості зсуву і крива течії є нелінійною, називають неньютонівськими рідинами (рис.2.2). За фізичними властивостями розрізняють три групи неньютонівських рідин.
1) Реологічно стаціонарні рідини, в яких швидкість зсуву в даній точці залежить тільки від напруження в цій точці, градієнт dw/dn не залежить від часу. В залежності від характеру функціональної залежності tт = f(dw/dn) їх поділяють на три типа:
а) бінгамівські рідини (дуже густі суспензії, пасти, шлами), які при малих напруженнях зсуву tт тільки незначним чином деформуються, а починають текти подібно ньютонівським рідинам тільки при перевищенні tт деякої величини t0 – границі текучості. Їх рух описується рівнянням Бінгама-Шведова:
tт -t0 = mп (dw/dn), (2.12)
де mп – кутовий коефіцієнт, який називають пластичною в’язкістю.
б) псевдопластичні рідини (розчини полімерів, целюлози, суспензії з асиметричною структурою часток) починають текти, як і ньютонівські рідини, при самих малих значеннях tт , а залежність напруження зсуву від швидкості деформації описується ступеневою функцією
tт = mк (dw/dn)n, (2.13)
де mк – уявна в’язкість, яка збільшується із зростанням реальної в’язкості і є мірою консистенції рідини, mк зменшується із зростанням швидкості зсуву. Величину n< 1 можна розглядати, як міру відхилення характеру руху даної рідини від ньютонівської.
в) ділатантні рідини (суспензії крохмалю, силікату калію, різноманітні клеї та інші суспензії з великою концентрацією твердої фази) подібно псевдо -пластичним не мають границі текучості (рівняння 2.13), але їх уявна в’язкість зростає із збільшенням швидкості зсуву (n> 1).
2) Реологічно нестаціонарні рідини, в яких швидкість зсуву залежить від тривалості дії напруження. В залежності від характеру впливу тривалості дії напруження на структуру рідини розрізняють:
а) тиксотропні рідини (фарби, кисломолочні харчові продукти), для яких характерне збільшення текучості із зростанням тривалості дії напруження зсуву, що викликане руйнацією структури рідини. Втім, після зняття напруження структура рідини поступово відновлюється і вона перестає текти.
б) реопектантні рідини (суспензії бентонітових глин, гіпсу, деякі колоїдні розчини) характеризуються тим, що їхня текучість із збільшенням тривалості дії напруження зсуву навпаки зменшується.
3) в’язкопружні (максвеллівські) рідини (смоли, високов’язкі емульсії і суспензії, пасти тістоподібної консистенції), які течуть під дією напруження t, але після зняття напруження частково відновлюють свою форму подібно до пружних твердих тіл.
Умовна в’язкість усіх неньютонівських рідин значно вище в’язкості води. Закони деформації і руху неньютонівських рідин є предметом окремої науки – реології. Реологічні властивості неньютонівських рідин визначаються на основі емпіричних рівнянь, які розглядаються в спеціальній літературі.
При контакті крапельної рідини з газом (парою) або іншою крапельною рідиною, яка практично не змішується з першою, на границі їхнього розділу виникають сили поверхневого натягу. Молекулярний тиск, що виникає при цьому на поверхні розділу за рахунок взаємного притягнення молекул, направлений всередину рідини по нормалі до її поверхні (в глибині об’єму рідини сили взаємного притягнення молекул взаємно врівноважуються) і намагається звести поверхню розділу до мінімуму. Тому краплі рідини в газі або бульбашки газу в рідині намагаються прийняти форму кулі. Таку властивість рідини називають міжфазним або поверхневим натягом. Для збільшення поверхні від мінімальної, тобто для утворення нової поверхні необхідна витрата деякої енергії. Роботу, яка необхідна для утворення одиниці нової поверхні, називають коефіцієнтом поверхневого натягу s = dA/dS [(Дж/м2)=(Н/м)]. Згідно з цим випливає, що s можна розглядати також як силу, яка діє на одиницю довжини l поверхні розділу рідини з навколишнім середовищем. Відповідно, повна сила поверхневого натягу дорівнює:
Fнат=s × l, Н. (2.14)
Величина s залежить від природи контактуючих фаз і зменшується із зростанням температури. Поверхневий натяг значною мірою впливає на розмір крапель або бульбашок при утворенні багатофазних систем.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.