Поделиться
ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ3.docx
Возведение в квадрат суммы и разности
двух выражений
Цели: закрепить умение возводить в квадрат двучлен по формуле; рассмотреть ряд задач, при решении которых применяется это умение.
Ход урока
I. Устная работа.
Выполните возведение в квадрат.
а) (–3х2у3)2; г)
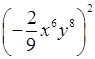; ж) (–п + 3)2;
б)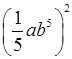 
; д) (х
– 8)2; з) (–а – 10)2.
в) (–0,7p2q4)2; е) (2у + 5)2.
II. Формирование умений и навыков.
1. № 814 (устно).
2. № 818 (а, в).
3. № 819.
Решение:
|
а) (х – 6)2 – х (х + 8) = 2; х2 – 12х + 36 – х2 – 8х = 2; –20х = –34;
х = х = 1,7. |
б) 9х (х + 6) – (3х + 1)2 = 1; 9х2 + 54х – 9х2 – 6х – 1 = 1; 48х = 2;
х = |
|
Ответ: 1,7. |
Ответ: |
|
в) у (у – 1) – (у – 5)2 = 2; у2 – у – у2 + 10у – 25 = 2; 9у = 27; у = 3. |
г) 16у (2 – у) + (4у – 5)2 = 0; 32у – 16у2 + 16у2 – 40у + 25 = 0; –8у = –25;
у = |
|
Ответ: 3. |
Ответ: 3 |
4. № 821.
При решении этого номера учащимся предстоит выполнять более сложные преобразования. Зачастую они делают очень распространенную ошибку: сначала умножают число на выражение в скобках, а потом результат возводят в квадрат.
Необходимо напомнить учащимся, что действие возведения в степень является приоритетным среди всех остальных, поэтому его выполняют в первую очередь.
Решение:
а) 7 (4а – 1)2 = 7 (16а2 – 8а + 1) = 112а2 – 56а + 7;
в)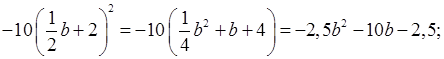 
д) 9с2
– 4 + 6 (с – 2)2 = 9с2 – 4 + 6 (с2
– 4с + 4) = 9с2 – 4 + 6с2 – 24с
+
+ 24 = 15с2 – 24с + 20.
5. № 823 (а, в).
Решение:
а) 
в) 
+ 2 =
= a3 – 3a + 2.
III. Итоги урока.
– Как возвести в квадрат сумму (разность) двух выражений?
– Каким из следующих выражений тождественно равно выражение (х – 2)2: (х + 2)2, (2 – х)2, (–2 – х)2, (–2 + х)2?
– Как выполнить следующие преобразования:
а) –2 (х – 4)2; б) (у + 3) (у – 2)2?
Домашнее задание: № 818 (б, г); № 820; № 822; № 823 (б, г).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
