ВОЗВЕДЕНИЕ В СТЕПЕНЬ ПРОИЗВЕДЕНИЯ И СТЕПЕНИ

Возведение в степень произведения и степени

Цели: вывести  правило  возведения  в  степень  произведения  двух и  более  сомножителей;  формировать  умение  вычислять  степень  произведения, а также рационально преобразовывать выражения, содержащие степень произведения либо предполагающие использование данного свойства.

Ход урока

I. Организационный момент

Устная работа.

Вычислите.

а) 2³ · 5³;                            в) 12²;                                   д) 5³ · ;                             ж) (bx)⁵;

б) 10³;                                г) 3² · 4²;               е) (2а)³;                       з) (ab)ⁿ.

II. Объяснение нового материала.

Доказательство:

(ab)ⁿ = (ab) · (ab) · ... · (ab) по определению степени п раз;

(ab) · (ab) · ... · (ab) = (aa...a)(bb...b) по свойствам умножения п раз п раз; (ab)ⁿ = aⁿbⁿ.

Вывод:

1) каждый множитель возводить в эту степень;

2) результаты перемножить.

Пример:

(abсd)⁴ = ...

Решение:

(abcd)⁴ = a⁴b⁴c⁴d⁴.

Рассмотреть пример 1 со с. 97 учебника.

III. Формирование умений и навыков.

1. № 428.

2. Выполните возведение в степень, представив предварительно основание степени в виде произведения множителей –1 и х:

а) (–х)²;                       б) (–х)⁸;                в) (–х)¹⁰⁰;                            г) (–х)^2п;

д) (–х)³;                       е) (–х)⁹;                ж) (–х)⁷¹;                            з) (–х)^{2п + 1}.

Решение:

а) (–х)² = ((–1) · х)² = (–1)² · х² = 1 · х² = х²;

е) (–х)⁹ = ((–1) · х)⁹ = (–1)⁹ · х⁹ = –1 · х⁹ = –х⁹;

г) (–х)^2п = ((–1) · х)^2п = (–1)^2п · х^2п = 1 · х^2п = х^2п;

з) (–х)^{2п + 1} = ((–1) · х)^{2п + 1} = (–1)^{2п + 1} · х^{2п + 1} = –1 · х^{2п + 1} = –х^{2п + 1}.

3. № 431.

Решение:

а и –а – противоположные числа.

а²;

(–а)² = ((–1) · а)² = (–1)² · а² = 1 · а² = а²,

значит, а² = (–а²).

4. № 432.

Решение:

Аналогично рассуждаем для остальных случаев.

5. № 433.

Решение:

6. № 434.

Для решения используем данные задачи № 432.

Решение:

Поверхность  куба  состоит  из  6  квадратов  площадью  а²,  то  есть равна 6а².

Если ребро куба увеличить в 3 раза, то площадь боковой грани составит 9а², а общая площадь поверхности равна 6 · 9а² или 54а².

Новая площадь больше в 9 раз, значит, и краски потребуется в 9 раз больше, то есть 40 · 9 = 360 г. Следовательно, 350 г краски на хватит.

Ответ: не хватит.

7. Представьте произведение в виде степени.

а) x⁵y⁵;                                         б) 36a²b²;                                           в) 0,001x³c³;

г) –х³;                                           д) –8х³;                               е) –32a⁵b⁵;

ж) x⁵y⁵z⁵;                                    з) 0,027a³b³c³;                  и) x³a³z³.

8. Вычислите значение выражения, используя свойство степени произведения.

а) 5³ · 2³;                                                     в) (0,5)³ · 60³;

б)  · 20⁴;                                        г) (1,2)⁴ · .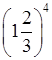

IV. Итоги урока.

– Сформулируйте определение степени с натуральным показателем.

– Сформулируйте правило возведения в степень произведения.

– Сколько  сомножителей  может  стоять  в  формуле  степени  произведения?

– Чему равно значение выражения (3 · 5 · 78)⁰?

Домашнее задание: № 429; № 430; № 435; № 436; № 437.