ВОЗВЕДЕНИЕ В СТЕПЕНЬ ПРОИЗВЕДЕНИЯ И СТЕПЕНИ1

Возведение  в степень произведения и степени

Цели: вывести правило возведения степени в степень; формировать умение  выполнять  преобразование  выражений,  содержащих  степень в степени.

Ход урока

I. Проверочная работа.

Вариант 1

1. Возведите в степень произведение.  а) (xyz)⁸;     б) ;           в) (–2а)³;                        г) .

2. Вычислите значение выражения.  а) 25² · 4²;        б)  · 9³;           в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение.   а) (abc)¹⁰;                 б) ;          в) (–4а)³;                        г) .

2. Вычислите значение выражения.  а) 20³ · 5³;        б)  · 25²;                 в) (–0,2)⁴ · 50⁴.

II. Объяснение нового материала.

1. Устная работа.

Представьте в виде степени.

а) (а⁵)³ = а⁵ · а⁵ · а⁵ = … ;                                      б) (у²)⁵ = … ;

в) (а^т)⁷ = … ;                                                                             г) (а^т)^п = … .

В результате появится запись:

2. Доказательство свойства можно оформить в виде таблицы.

Свойство. При возведении степени в степень основание оставляют тем же, а показатели перемножают.

Подчеркиваем, что формулу можно применять в следующем виде:

III. Формирование умений и навыков.

1. № 438 (устно).

Решение:

а) (х³)² = х^{3 · 2} = х⁶;

з) (b⁵)² = b^{5 · 2} = b¹⁰.

2. № 440, № 441.

№ 441.

Решение:

а) а^п · а³ = а^{п + 3};

г) (а²)^т = а^2т.

3. № 443, № 445, № 446.

№ 443.

Решение:

а) 2²⁰ = 2^{2 · 10} = (2²)¹⁰;                             б) 2²⁰ = 2^{4 · 5} = (2⁴)⁵;

в) 2²⁰ = 2^{5 · 4} = (2⁵)⁴;                 г) 2²⁰ = 2^{10 · 2} = (2¹⁰)².

№ 445.

Решение:

12 = 1 · 12;                  а¹² = (а¹)¹²;

12 = 2 · 6;                    а¹² = (а²)⁶;

12 = 3 · 4;                    а¹² = (а³)⁴;

12 = 4 · 3;                    а¹² = (а⁴)³;

12 = 6 · 2;                    а¹² = (а⁶)²;

12 = 12 · 1;                  а¹² = (а¹²)¹.

№ 446. Решение:

а² = т;

а⁶ = а^{2 · 3} = (а²)³ = т³.

4. Представьте выражение в виде квадрата числа.

а) а⁴;                                б) b⁶;                    в) d⁸;                   г) c¹⁰;

д) d²⁰;                              е) ;                               ж) 1;                           з) .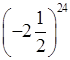

5. № 447, № 449 (а, б), № 450 (а, б).

№ 447.

Решение:

а) x³ · (x²)⁵ = x³ · x^{2 · 5} = x³ · x¹⁰ = x^{3 + 10} = x¹³;

б) (a³)² · a⁵ = a^{3 · 2} · a⁵ = a⁶ · a⁵ = a^{6 + 5} = a¹¹;

в) (a²)³ · (a⁴)² = a^{2 · 3} · a^{4 · 2} = a⁶ · a⁸ = a^{6 + 8} = a¹⁴;

г) (x²)⁵ · (x⁵)² = x^{2 · 5} · x^{5 · 2} = x¹⁰ · x¹⁰ = (x¹⁰)² = x^{10 · 2} = x²⁰;

д) (a³a³)² = (a⁶)² = a^{6 · 2} = a¹²;

е) (aa⁶)³ = a³ · (a⁶)³ = a³ · a^{6 · 3} = a³ · a¹⁸ = a^{3 + 18} = a²¹.

№ 449.

Решение:

а) x⁵ · (x²)³ = x⁵ · x⁶ = x¹¹;

б) (x³)⁴ · x⁸ = x¹² · x⁸ = x²⁰.

№ 450.

Решение:

а)  = 2⁴ = 16;

б)  = 5.

6. (Устно.) Найдите примеры, в которых допущена ошибка.

1) (ab)³ = a³b³;                                         5) (–3²)³ = 3⁶;

2) (–2bc)² = –4b²c;                   6) (c⁴)²c³ = c⁹;

3) (2 · 5)⁴ = 10000;                   7)  = a²⁴;

4) (–3³)² = 3⁶;                                             8)  = 2⁶a⁶b¹⁴.

IV. Итоги урока.

– Сформулируйте определение степени с натуральным показателем.

– Сформулируйте правило возведения степени в степень. приведите примеры.

– Каков алгоритм возведения степени в степень?

– Чему равно значение выражения: ; (x³)⁰?

Домашнее задание:  № 439;  № 442;  № 444;  № 448;  № 449  (в, г);
№ 450 (в, г).

Вариант 1

1. Возведите в степень произведение.  а) (xyz)⁸;               б) ;            в) (–2а)³;                          г) .

2. Вычислите значение выражения.  а) 25² · 4²;                 б)  · 9³;            в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение.   а) (abc)¹⁰;           б) ;            в) (–4а)³;                          г) .

2. Вычислите значение выражения.  а) 20³ · 5³;                 б)  · 25²;                  в) (–0,2)⁴ · 50⁴.

Вариант 1

1. Возведите в степень произведение.  а) (xyz)⁸;               б) ;            в) (–2а)³;                          г) .

2. Вычислите значение выражения.  а) 25² · 4²;                 б)  · 9³;            в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение.   а) (abc)¹⁰;           б) ;            в) (–4а)³;                          г) .

2. Вычислите значение выражения.  а) 20³ · 5³;                 б)  · 25²;                  в) (–0,2)⁴ · 50⁴.

Вариант 1

1. Возведите в степень произведение.  а) (xyz)⁸;               б) ;            в) (–2а)³;                          г) .

2. Вычислите значение выражения.  а) 25² · 4²;                 б)  · 9³;            в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение.   а) (abc)¹⁰;           б) ;            в) (–4а)³;                          г) .

2. Вычислите значение выражения.  а) 20³ · 5³;                 б)  · 25²;                  в) (–0,2)⁴ · 50⁴.

Вариант 1

1. Возведите в степень произведение.  а) (xyz)⁸;               б) ;            в) (–2а)³;                          г) .

2. Вычислите значение выражения.  а) 25² · 4²;                 б)  · 9³;            в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение.   а) (abc)¹⁰;           б) ;            в) (–4а)³;                          г) .

2. Вычислите значение выражения.  а) 20³ · 5³;                 б)  · 25²;                  в) (–0,2)⁴ · 50⁴.

Вариант 1

1. Возведите в степень произведение.  а) (xyz)⁸;               б) ;            в) (–2а)³;                          г) .

2. Вычислите значение выражения.  а) 25² · 4²;                 б)  · 9³;            в) (–0,5)³ · 40³.

Вариант 2

1. Возведите в степень произведение.   а) (abc)¹⁰;           б) ;            в) (–4а)³;                          г) .

2. Вычислите значение выражения.  а) 20³ · 5³;                 б)  · 25²;                  в) (–0,2)⁴ · 50⁴.