Время удержания энергии в токамаке

 Время удержания энергии в токамаке.

Мы видим‚ что с ростом В_q и с ростом а nt быстро растет‚ причем в основном не за счет n‚ а за счет t. Отсюда следует‚ что частицы уносят энергию из плазмы медленнее‚ когда размеры плазмы велики и В_q — большое. Попытаемся выяснить‚ каким образом энергия уходит из плазмы в токамаке.

Даже если МГД-неустойчивость застабилизировали и плазма не касается стенок как целое‚ частицы плазмы все же покидают ее и уносят энергию на стенки. Уход частиц из плазмы происходит за счет диффузии ионов и электронов поперек магнитного поля. Т.о.‚ время удержания энергии в плазме (если пренебречь остыванием за счет тормозного и циклотронного излучения) обусловлено временем диффузии или‚ что более вероятно‚ скоростью диффузии. Вопрос о скорости диффузии имеет значение первостепенной важности‚ т.к. если диффузия будет слишком быстрой‚ то критерий Лоусона не будет достигнут при различных n.

1. Классическая диффузия.

Без магнитного поля диффузия идет как в классической теории газов: в течение одного столкновения частица смещается на l. Если ее скорость V‚ то коэффициент диффузии:

;                                               (13.1)

Если есть магнитное поле‚ то‚ принимая‚ что вдоль магнитного поля нет градиента n и по азимуту тоже‚ и‚ следовательно‚ диффузия возможна по одной координате‚ перпендикулярной В (тройка из знаменателя исчезнет)‚ мы получим:

‚                          (13.2)

где l — характерный размер смещения за время между соударениями t. Но если в отсутствие магнитного поля l — есть характерная длина свободного пробега‚ то при наличии магнитного поля l играет роль ларморовского радиуса. r_с — характерная длина смещения частицы поперек поля после столкновения. Поэтому:

                 .                                                                              (13.3)

Т.к.                 ‚                                                           (13.4)

то                    .                                                                   (13.5)

Теперь уточним значения параметров‚ входящих в формулу (13.5). Во-первых‚ электроны и ионы могут иметь различную температуру‚ поэтому заменяем

                                                                                          (13.6)

Во-вторых‚ замагниченность определяется электронами‚ т.к. их ларморовский радиус меньше и они диффундируют медленнее (а ионы идут амбиполярно с ними). Поэтому

                                                                                             (13.7)

И‚ наконец‚ можно строго доказать (см. Арцимович УТС  М.‚ 1963 стр.98)‚ что столкновения однотипных частиц между собой не приводят в магнитном поле к смещению плазмы как целого поперек магнитного поля. Поэтому нужно учитывать только столкновения различных частиц‚ т.е. электрон-ионные столкновения. Тогда заменим

                                                                                                  (13.8)

и получим формулу

                                                                               (13.9)

(мы заменили ). Подставляя сюда значения констант и используя формулу (2.11)‚ т.е. ‚

получим

                 .                                       (13.10)

Чтобы сравнить замагниченную и незамагниченную

                         (13.11)

из (13.9) и (13.11)

тогда 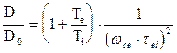             .                                      (13.12)

Из (13.12) видно‚ что магнитное поле колоссально снижает скорость диффузии‚ а именно D~1/B². Для термоядерной плазмы‚ например‚ ‚ В=50кГс и D /D₀~10^-16. Таким образом‚ согласно классической теории‚ магнитное поле должно немедленно решить проблему удержания и термоизоляции плазмы.

2.          Бомовская диффузия.

Экспериментальная проверка‚ однако‚ дала неутешительные результаты.

Формула (13.12) имела место лишь в спокойной плазме‚ где есть полная ионизация и T_e=T_i=T_g‚ нет никаких пучков частиц и т.д.‚ т.е. в равновесной плазме. Однако малейший уход от равновесных условий приводит к резкому возрастанию коэффициента диффузии поперек В. Выяснилось‚ что дело кинетических неустойчивостях (микронеустойчивостях)‚ которые‚ хотя и не приводят к макроскопическим деформациям плазменного шнура‚ но ведут к возникновению пульсирующих электромагнитных полей в плазме‚ которые резко (на порядки величин) увеличивают коэффициент поперечной диффузии.

Американский физик D.Bohm предложил (без вывода) эмпирическую формулу для коэффициента поперечной диффузии в плазме с колебаниями:

                 ‚                                                                (13.13)

или в CGSE

                 .                                                                        (13.14)

Легко видеть‚ что формула Бома не является произвольной и содержит в себе турбулентную природу диффузии. В самом деле‚ коэффииент диффузии можно записать‚ как и (13.3)

                 ‚                                                                             (13.15)

где l — характерный размер турбулентности‚ t — характерное время пролета частиц сквозь один вихрь. Пусть флюктуация (турбулентность‚ вихрь) имеет тепловой характер. Тогда на длине l произойдет отклонение от нейтральности‚ которое дает флюктуационный потенциал:

                                                                                               (13.16)

и поле‚ соответственно

                 ‚                                                                             (13.17)

откуда

                 .                                                                                (13.18)

В скрещенных полях Е_tr и В происходит дрейф частиц со скоростью

                 ‚                                                          (13.19)

значит:

                 .                          (13.20)

Мы получили с точностью до численного множителя формулу Бома (13.13).

Следует отметить‚ что Бомовская диффузия была домокловым мечом‚ угрожавшим принципиальной возможности осуществления УТС. Например‚ для термоядерных условий: T_e=T_i=10кэВ‚ В=50кГс‚ n=5×10¹⁴‚ как мы видели‚ классика дает снижение коэффициента диффузии поперек В по сравнению с D₀ в 10¹⁶ раз‚ а бомовская диффузия — существенно меньше. Приведем оценки:

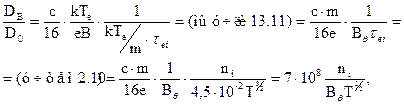
Т.е.

                                                                             (13.21)

для указанных параметров D_B/D₀~10^-9‚ тогда как‚ согласно классике (13.12)‚ D/D₀~10^-16. Итак‚ бомовская диффузия идет в миллионы раз быстрее‚ т.е. время жизни плазмы в миллионы раз короче.

3. Неоклассическая диффузия Пфирша — Шлютера.

На этот раз природа была милостлива и в экспериментах на токамаках в 67 — 68 гг. измеренные времена жизни оказались в 10¸100 раз больше бомовских‚ хотя на стеллараторах t была порядка бомовского. Однако‚ стало ясно‚ что бомовская диффузия не универсальна. Нужно было снова вернуться к физическим основам диффузии в плазме. Это сделали еще раньше Пфирш и Шлютер (1962 г.)‚ которые рассмотрели траектории частиц в токамаке и нашли‚ что строгий анализ приводит в качестве шага диффузии не к ларморовскому радиусу r‚ а к несколько большей величине:

                                                                                      (13.22)

Коэффициент=q — есть запас устойчивости Крускала — Шафранова. Поэтому шаг дифффузии: =qr                                                               (13.23)

Обычно в токамаках q=3 — 4 и‚ поскольку коэффициент диффузии ~2  (13.3)‚ то это приводит к росту D  в 10¸20 раз. Эта теория предусматривает классический характер диффузии‚ но с новым шагом‚ поэтому она получила название ”неоклассическая диффузия”. Подставив в (13.23) выражение для r‚ получим:

                          (13.24)

Итак‚ шаг диффузии определяется не полем B_q‚ а полем В_j !!!

Это важнейший результат неоклассической теории. Поле В_q — удерживает шнур в устойчивом состоянии‚ но не определяет диффузию. Диффузию ограничивает поле В_j — полоидальное поле.[L1] 

4.Развитие неоклассической теории А.А. Галеевым и Р.З. Сагдеевым.

Галеев и Сагдеев учли‚ что частицы в поле токамака разбиваются на два класса: пролетные и запертые. Пролетные циркулируют по тору вдоль винтовых силовых линий магнитного поля. Это также частицы‚ которые имеют малый угол a между вектором скорости и направлением силовой линии. При своем движении вдоль спиральной силовой линии (т.е. скользя по данной магнитной поверхности) частица попадает то в более сильное (внутри тора)‚ то в более слабое (внутри тора) магнитное поле. Если угол a мал‚ то частица пролетная‚ а если угол a велик‚ то частица может отразиться от более сильного поля (как в mirror) и пойти обратно. Затем‚ идя обратно‚ она вновь попадает во внутреннюю часть тора в более сильное поле и снова отражается. Т.о.‚ частица оказывается запертой и ее ларморовский кружок описывает замкнутую траекторию‚ имеющую в сечении шнура проекцию в форме банана. Этот режим движения запертой частицы называется банановым режимом. Ширина проекции d и является характерным шагом диффузии‚ т.е.

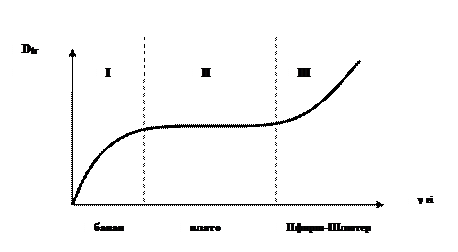
Такое разделение на запертые и пролетные частицы возможно только при не слишком большом n и достаточно большом Т‚ т.е. когда  не слишком велико‚ т.к. частые столкновения приведут к перемешиванию пролетных и запертых частиц. Галеев и Сагдеев показали‚ что зависимость D  от  разделяется на три области:

 область I (малые ) соответствует разделению на пролетные и запертые частицы‚ причем общее время жизни определяется именно запертыми частицами.

В этой области “банановой” диффузии :

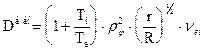                 .                                                      (13.26)

Вторая область II‚ где влияние столкновений начинает слабо действовать‚ называется областью плато. Здесь

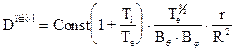                                                                (13.27)

И‚ наконец‚ область III‚ где столкновения перемешивают частицы частицы и они практически не захватываются на банановые траектории — это область диффузии Пфирша — Шлютера.

В токамаках обычно осуществляется реакция I‚ т.е. имеет место банановая диффузия. Отношение D^бан/D₀ в термоядерных условиях n=5×10¹⁴ см^-3‚ Т_e=T_i=10⁸°К‚  ;         В_q=50 кГс‚            r/R=1/3;           В_j=5 кГс равно

                 D^бан/D₀=10^-13                                                (13.28)

Т.о.‚ неоклассическая диффузия идет в токамаках в 10³ раз быстрее‚ чем классическая‚ но в 10⁴ раз медленнее‚ чем бомовская:

                        (13.29)

Скачано с www.znanio.ru