ВЫНЕСЕНИЕ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ

вынесение общего множителя за скобки

Цели: ввести понятие разложения многочлена на множитель; изучить способ вынесения общего множителя за скобки и формировать умение его применять.

Ход урока

I. Устная работа.

1. Выполните умножение.

а) 3x (2x² – 5);                          в) 5y⁴ ;

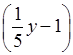б) a² (a + 2);                      г) –ab (a² – b).

2. Найдите наибольший общий делитель чисел.

а) 10, 15 и 25                           в) 8, 12 и 16;

б) 6, 9 и 21;                              г) 12, 18 и 30.

II. Объяснение нового материала.

Вынесение общего множителя за скобки является обратной задачей к умножению одночлена на многочлен. Поэтому данный материал будет понят учащимися только в том случае, если они хорошо усвоили предыдущую тему.

Объяснение проводится в несколько этапов.

1. Начать лучше с постановки проблемной задачи.

Задача. После умножения некоторого одночлена на некоторый многочлен был получен многочлен 4х² – 6х⁴. Какой одночлен на какой многочлен умножали?

2 (2х² – 3х⁴), х (4х – 6х³), 2х² (2 – 3х²) и т. п.

Можно рассмотреть ещё несколько подобных задач. Главное, что такие задачи всегда имеют решение и являются обратными к выполнению умножения одночлена на многочлен.

2.Представление многочлена в виде произведения двух или нескольких многочленов называется разложением многочлена на множители.

Данная операция является очень полезной при решении ряда задач, которые впоследствии будут рассмотрены.

3. Вернуться к разложенным на множители многочленам и обратить внимание  учащихся,  что  для  задач  наиболее  целесообразным  является нахождение  «наибольшего»  общего  множителя  каждого  члена  много-члена. Поэтому в рассмотренном примере лучше записать следующее равенство:

4х² – 6х⁴ = 2х² (2 – 3х²).

Данный способ разложения многочлена на множители называется вынесением общего множителя за скобки.

4. Разобрать  несколько  примеров  вынесения  за  скобки  общего множителя:

а) 8х²у – 6х;

б) 3а⁴ + 9а² – 6а;

в) пример 1 из учебника.

Сделать вывод: при вынесении общего множителя за скобки среди модулей коэффициентов берут их наибольший общий делитель, а переменные, выносимые за скобки, берут с наименьшим показателем.

III. Формирование умений и навыков.

1. № 654; № 655 (а, в, д, ж, и); № 656 (а, в, д).

В данных заданиях у многочленов общим множителем является либо только число, либо только буква. Необходимо, чтобы учащиеся сначала научились находить такие простые общие множители.

2. № 657 (а, в, д, и, л); № 659.

Здесь общие множители находить сложнее. Важно, чтобы учащиеся отыскивали правильно «наибольшие» общие множители.

№ 659.

Решение:

а) 14x + 21y = 7 (2x + 3y);

б) 15a + 10b = 5 (3a + 2b);

в) 8ab – 6ac = 2a (4b – 3c);

г) 9xa + 9xb = 9x (a + b);

д) 6ab – 3a = 3a (2b – 1);

е) 4x – 12x² = 4x (1 – 3x);

ж) m⁴ – m² = m² (m² – 1);

з) c³ + c⁴ = c³ (1 + c);

и) 7x – 14x³ = 7x (1 – 2x²);

к) 16y³ + 12y² = 4y² (4y + 3);

л) 18ab³ – 9b⁴ = 9b³ (2a – b);

м) 4x³y² – 6x²y³ = 2x²y² (2x – 3y).

IV. Итоги урока.

– Что называется разложением многочлена на множители?

– Какой способ разложения многочлена на множители мы узнали на этом уроке?

– В чём состоит способ вынесения общего множителя за скобки?

– Как отыскивать выносимый за скобки общий множитель?

Домашнее задание: № 655 (б, г, е, з); № 656 (б, г, е); № 657 (б, г, е, з, м); № 658.