ВЗАИМНООБРАТНЫЕ ЧИСЛА

ВЗАИМНООБРАТНЫЕ ЧИСЛА

Урок 1

Цели: ввести понятие взаимно обратных чисел; повторить правило умножения дробей, сокращения дробей; развивать логическое мышление учащихся.

Ход урока

I. Анализ контрольной работы.

1. Сообщить результаты контрольной работы.

2. Выполнить на доске задания, вызвавшие затруднения у учащихся.

3. Устно решить № 582 и 586 (а; б).

II. Изучение нового материала.

1. Выполнить умножение чисел:

2. Определение взаимно обратных чисел.

 при а ≠ 0 и в ≠ 0.

3. Найти число, обратное числу 3

Запишем число 3 в виде неправильной дроби:  Значит, обратным  будет число

III. Закрепление изученного материала.

1. Решить № 577 (а; г; д) на доске и в тетрадях.

2. Решить № 578 (а; е) на доске и в тетрадях; № 578 (б; в; г) решить с комментированием на месте.

Решение.

3. Решить уравнения № 564 (а; б).

Решение.

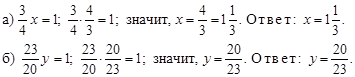
4. Повторение ранее изученного материала:

а) решить № 583;

б) самостоятельно решить № 590 (1);

в) решить на доске и в тетрадях № 589.

Решение.

Вспомнить правило нахождения среднего арифметического чисел.

Пусть первое число равно х, тогда второе число (х + 0,9), а третье число 2х. Составим и решим уравнение:

(х + х + 0,9 + 2х) : 3 = 3,1

4х + 0,9 = 3,1 · 3

4х + 0,9 = 9,3

4х = 9,3 – 0,9

4х = 8,4

х = 8,4 : 4 = 2,1.

Первое число равно 2,1; второе число 2,1 + 0,9 = 3; третье число 2,1 · 2 = 4,2.

Ответ: 2,1;  3;  4,2.

IV. Итог урока.

1. Ответить на вопросы:

а) Какие числа называют взаимно обратными?

б) Как записать число, обратное дроби

в) Как записать число, обратное натуральному числу?

г) Как записать число, обратное смешанному числу?

2. Привести свои примеры.

Домашнее задание: п. 16, решить № 591 (а); № 592 (а; в), № 595 (а).