Wetting, capillary phenomena Lab work (1)

Name _________________________________   Class _________   Date _______

Laboratory work "Measurement of liquid surface tension"

Objective:

Study of the phenomenon of surface tension; experimental determination of the coefficient of surface tension of water by the method of separation of the loop and drops

Materials:

Dynamometer type DPN with accessories; tripod for frontal work; distilled water; ruler measuring 30 cm with millimeter divisions.

Content and method of work

The free surface of the liquid in a state of equilibrium tends to a minimum, the liquid is as if tightened by an elastic surface film, which tends to reduce its area.

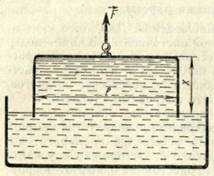
Figure 1

During the formation of a thin film of width L (Fig. 1) along the boundary of the surface of the liquid, the surface tension force F is equal to

                                                               (1)

Where σ is the surface tension; multiplier 2 stands for the reason that the film has two surfaces.

From here

(2)

The modulus of the surface tension force F is measured by a DPN-type sensitive dynamometer, and the film width, equal to the width of the wire loop, is measured by a measuring ruler. Dynamometer type DPN (Fig. 2) consists of a housing 3, inside which is placed the measuring spring 5, which has a straight end with an open hook 7. The hook is designed to connect the loop 8 with the measuring spring of the dynamometer. To read the readings on a scale, an arrow 6 is fixed on the measuring spring. The test liquid is poured into a glass cup 9.

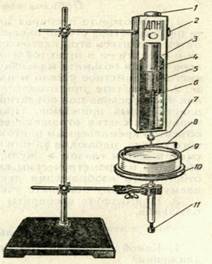
Figure 2

To measure the surface tension, the wire loop is completely immersed in the fluid and then slowly pulled out of the fluid. In this case, a film is formed on the loop. When the elastic force of the spring of the dynamometer becomes equal in magnitude to the force of surface tension F, the film is broken

Force determination of the surface tension coefficient: the liquid surface tension coefficient σ is numerically equal to the force acting per unit length of the phase line. The desire of the liquid to reduce the surface area is manifested in the fact that a small volume of liquid takes the form close to the ball. In this case, the force of gravity acting on the drop is small, and the shape of the liquid drop is determined by the surface energy. This also explains the spherical shape of droplets in a state of weightlessness. Figure 3 shows a drop of water when detached.

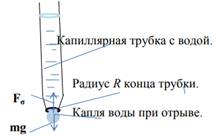
Figure 3

Before separation of a drop, a neck is formed, the radius of which is somewhat less than the radius of the tube. The surface tension force acts along the circumference of this neck. Fσ, upward, which at the moment of separation is equal to the force of gravity. If the neck radius r = R, that Fσ =2πRσ = m₁g, where m₁- mass of one drop of liquid. Knowing the mass of one drop of liquid, you can determine σ: σ = m₁g/2πR.

A narrow tube (pipette) with a tap filled with water is fixed on the tripod. The radius of the tip of the tube is R = 0.7 mm. There is also a container for collecting drops and electronic scales.

Procedure

Task 1. Measurement of the surface tension of water by the method of separation loop

1.       Examine the device dynamometer DPN.

2.       Prepare the instrument for measurement. To do this, put the loop 8 on the open hook 7 (see Fig. 2). While holding the set screw 1, unscrew the locking screw 2. Turning the cup 4 and pressing the screw head 1, set the pointer of the dynamometer to the zero scale division. Tighten the locking screw.

3.       Pour distilled water into the cup 9 and place it on the stand 10. Rotate the screw of the holder 11, raise the cup with liquid to such a level that the loop is completely submerged in water.

4.       Slowly lower the cup of water. To do this, unscrew the screw of the holder 11 until the film of fluid that breaks behind the loop breaks. Note on the scale of the dynamometer film breakage force.

5.       Calculate the surface tension using the formula (2).

6.       Repeat the measurement three times. Calculate the average surface tension value.

Task 2. Determination of the coefficient of surface tension of water by the method of separation of droplets.

1.       Weigh an empty drop collection container on electronic scales and record the resulting mass value m0 in Table 1. (First make sure that there is no water in the container.)

2.       When opening the tap (using another dish), ensure that separate water drops form during the process of fluid flow.

3.       Having substituted capacity for collecting drops, drop in it N drops of water. Drops of water should not merge with each other. The number of drops is shown in table 1. (May vary by teacher.)

4.       Weigh the weight of the water tank m on the electronic scale. Complete the column headings and write the data in the table.

5.       After weighing it is necessary to pour water from the tank, wipe the tank dry..

6.       Perform steps 2-5 for specified values ​​of N.

Table

Data Analysis (Processing Results)

1.      For each N (number of droplets), find the mass of N drops of water. To do this, the mass of the tank without water must be subtracted from the mass of the container with water: m_N = m – m_o. Data write to the table.

2.      For each N, calculate the mass of one drop: m₁ = m_N / N. Data write to the table.

3.      Calculate the length of the phase boundary, which is equal to the length of the neck of a droplet before its separation L = 2πR. We assume that the neck radius r is equal to the inner radius of the tip of the tube R = 0.7 mm.

4.      Using the formula for each case, calculate the coefficient of the surface tension of the fluid σ. Calculations carried out in the SI. Write the data in the table.

5.      Find the average σ_ave.

Questions

1) What is called liquid surface tension?

2) Why is there a factor of 2 in formula (2)?

3) Why was the measurement of the modulus of the surface tension of water not carried out with a straight wire, but with a loop having a U-shape?

4) What factors determine the coefficient of surface tension?

5) What are surfactants? Give examples of their use.

6) Explain why, in the absence of external forces, the shape of the liquid droplets is spherical?

7) What are capillary phenomena? Explain the phenomenon of rising fluid in the capillaries under the condition of wetting. What determines the height of the rise?

8)