Y=sinx ֆունկցիայի հատկություններն ու գրաֆիկը

y=sinx ֆունկցիայի հատկություններն ու գրաֆիկը

     Դիտարկենք y=sinx ֆունկցիան, որի արժեքը x կետում հավասար է x ռադիան անկյան սինուսին:

 1. y=sinx ֆունկցիայի որոշման տիրույթն ամբողջ թվային առանցքն է՝ D(sinx)=R:

 2. y=sinx ֆունկցիայի արժեքների բազմությունը [−1;1] հատվածն է:

 3. y=sinx ֆունկցիան պարբերական է T=2π պարբերությամբ: 

 4. y=sinx ֆունկցիան կենտ է:

 5. sinx=0, երբ x=πn,n∈Z: 

 6. y=sinx ֆունկցիայի մեծագույն արժեքը 1-ն է, որը ֆունկցիան ընդունում է  x=π/2+2πn,n∈Z կետերում: 

 7. y=sinx ֆունկցիայի փոքրագույն արժեքը −1-ն է, որը ֆունկցիան ընդունում է x=−π/2+2πn,n∈Z կետերում:

 8. y=sinx ֆունկցիան դրական է (2πn;π+2πn) արգումենտների համար, և բացասական է

(π+2πn;2π+2πn) արգումենտների համար, որտեղ n∈Z:

 9. y=sinx ֆունկցիան աճում է [−π/2+2πn;π/2+2πn] հատվածներում և նվազում է [π/2+2πn;3π/2+2πn] հատվածներում, որտեղ n∈Z:

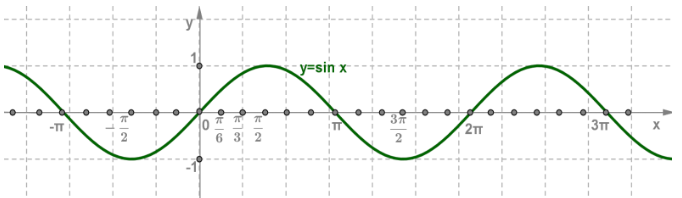
    Հաշվի առնելով թվարկված հատկությունները, կառուցում ենք y=sinx ֆունկցիայի գրաֆիկը: