y=tgx ֆունկցիայի հատկություններն ու գրաֆիկը

y=tgx ֆունկցիայի հատկություններն ու գրաֆիկը

    y=tgx ֆունկցիան որոշված է  x≠π/2+πn,n∈Z արգումենտների համար, կենտ է և պարբերական՝  π պարբերությամբ:

    Ուստի, ֆունկցիայի գրաֆիկը բավական է կառուցել [0;π/2) բազմության վրա:

Ընտրենք մի քանի կետեր, որոնցով անցնում է տանգենսի գրաֆիկը՝

 tg0=0    tgπ=tgπ/4=1     tgπ/3=:

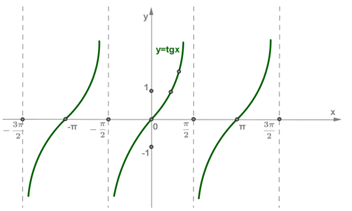
     Կառուցում ենք գրաֆիկի ուրվագիծը, ապա այն կոորդինատների սկզբնակետի նկատմամբ համաչափ արտապատկերում: Ստանում ենք y=tgx ֆունկցիայի գրաֆիկը (−π/2;π/2)միջակայքում: Գրաֆիկի այս մասը անվանում են տանգենսի գլխավոր ճյուղ:

    Օգտվելով y=tgx ֆունկցիայի պարբերականության հատկությունից՝ գրաֆիկը շարունակում ենք դեպի աջ և ձախ: Ստանում ենք հետևյալ գրաֆիկը՝

    y=tgx ֆունկցիայի հատկությունները

 1. y=tgx ֆունկցիան որոշված է x≠π2+πn,n∈Z թվերի համար:

 2. y=tgx ֆունկցիայի արժեքների բազմությունը ամբողջ թվային առանցքն է՝ E(tgx)=R:

 3. y=tgx-ը π-պարբերական ֆունկցիա է:

 4. y=tgx-ը կենը ֆունկցիա է:  

 5. tgx=0, եթե x=πn,n∈Z:

 6. y=tgx ֆունկցիայի արժեքները դրական են (πn;π/2+πn),n∈Z միջակայքերում և բացասական են (−π/2+πn;πn),n∈Z. միջակայքերում:

 7. y=tgx ֆունկցիան աճում է (−π/2+πn;π/2+πn),n∈Z. միջակայքերում:

 8. y=tgx ֆունկցիան էքստրեմումի կետեր չունի: