Задачи ЕГЭ,банковские задачи

Подготовка  к ЕГЭ:

Тема: «Решение финансовых задач»

Форма урока: занятие-практикум.

Цели: повторение теоретического материала по теме «Проценты. Вклады и кредиты», составление математической модели  практических задач, формирование практических навыков решения задач №17 единого государственного экзамена.

Задачи:

- способствовать запоминанию основной терминологии, умению построить математическую модель задачи;

- развитие вычислительных  навыков учащихся;

-формирование логического мышления;

- способствовать развитию интереса к математике; умений применять новый материал на практике и в жизни.

- развитие коммуникативных умений учащихся  через организацию групповой,  фронтальной работы на уроке. 

                                                           Ход урока:

I. Организационный момент (Урок сопровождается компьютерной презентацией.)

Сегодня мы рассмотрим более жизненную задачу из ЕГЭ по математике, которая имеет прямое отношение к нашей российской экономике.

 Сегодня мы рассмотрим задачи про вклады, проценты и кредиты, задачи с процентами в едином  государственном экзамене по математике под №17, за решение этой задачи согласно спецификациям ЕГЭ предлагается сразу три первичных балла, т. е. экзаменаторы считают эту задачу одной из самых сложных. Решение задачи №17 включает в себя обязательное построение математической модели, то есть это обычная текстовая задача, но с экономическим (финансовым) уклоном и чаще всего с большим количеством вычислений.

Чтобы правильно решать такие задачи, необходимо владеть формулой сложных процентов.

Но прежде чем браться за сложные задачи давайте повторим, что вы запомнили о процентах, вкладах и кредитах.

II. Актуализация знаний учащихся

Фронтальная работа с классом –повторение теоретического материала:

1.     Что необходимо знать и понимать при решении задач на проценты:

- Что такое процент? (1% - это одна сотая часть чего-либо)

За 100%  принимаем ту величину, с которой сравниваем;

- Какие проценты бывают в банковских операциях? (Простые и сложные, кредитные и депозитные)

- Чем отличаются эти виды процентов?

Устная работа (на слайдах 1-3):

1)Число  х  увеличили на 50%.  Во сколько раз возросло число  х? (в 1,5 раза)

2) Число  у  увеличили на 120%.  Какое число получилось? (2,2у)

3) Число  z  уменьшили на 13%.  Какое число получилось? (0,87z)

2.     Какую основную терминологию мы знаем при решении содержательных задач из различных областей, в частности экономических?

 S - сумма кредита  (руб.)

k   - процентная ставка   (%)

m= 1+ 0,01k. - коэффициент увеличения

Х- ежегодная выплата--  платеж (руб.)

п – срок кредита ( месяц, год)

3.     Работа с формулами.

В дальнейшем для работы нам нужны будут формулы, которые вы должны для себя прочно запомнить. Посмотрите на доску, соотнесите название формулы и ее содержание.  (задание по формату соответствует заданиям ЕГЭ базового уровня. Ученики называют ответы, учитель маркером вносит их в таблицу)    А3 Б1 В5 Г2 Д4Формулы для подсчета процентов:

если величину  S увеличить на k %, то получим S(1+0,01k)

если величину S уменьшить на k %, то получим S(1- 0,01k)

если величину S дважды увеличить на k %, то получим S(1+0,01k)²

если величину S дважды уменьшить на k %, то получим S(1- 0,01k)².

Слайд-4(нахождение %) Задача .

Антикварный магазин приобрел старинный предмет за 30 тыс. р. и повысив цену на 60 %. Но этот предмет был продан лишь через неделю, когда магазин снизил его новую цену на 20 %. Какую прибыль получил магазин при продаже антикварного предмета?

4.     Молодцы ребята! А сейчас мы переходим к задачам связанным с кредитами и вкладами. Скажите  пожалуйста, что вы знаете о видах платежей в кредитовании?

III.  Решение задач из открытого банка задач

Задача № 1.

Василий взял кредит в банке на сумму 804 000 рублей. Схема выплата кредита такова: в конце каждого года банк увеличивает на 10 процентов оставшуюся сумму долга, а затем Василий переводит в банк свой очередной платеж. Известно, что Василий погасил кредит за три года, причем каждый его следующий платеж был ровно вдвое меньше предыдущего. Какую сумму Василий заплатил в третий раз? Ответ дайте в рублях.

S= 804 000 руб.             k=1+0.1=1.1              n=3

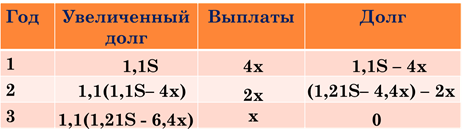
Так как нам необходимо , вычислить какую сумму  В. заплатил в третий раз,  то именно ее мы обозначим за  х.  Тогда в предыдущий год он сделал платеж в два раза больше 2х, а в первый раз - 4х руб. В первый год с учётом процентного увеличения долг составил 1,1S, а после выплаты 1,1 S- 4х. Во второй год после увеличения 1,1 (1,1 S- 4х), после выплаты                         1,1 (1,1 S - 4х) - 2х = (1,21S - 4,4х) -2х= 1,21S – 6,4х.

И третий год  1,1 (1,21S – 6,4х) – х= 0

Решите это уравнение относительно х.

1,331S -7,04х – х=0

1,331S -8,04х=0

1,331S= 8,04х

Х= 1,331S /8,04

Теперь можно подставить вместо S значение суммы взятой в кредит 804 000 руб:

Ответ:  последний платёж 133100 руб.

IV. Подведение итогов

«Банковские» задачи  на ЕГЭ — это достаточно сложные задачи. Но думаю и с ними вы сможете справится.  Для решения задачи №17  вам понадобятся самые основные формулы вычисления выплат, сумм, процентной ставки,  вычислительные навыки..

Основная формула всего одна — это вычисление размера долга в зависимости от срока кредита.

Домашнее задание  Выполнить тренировочную работу  ЕГЭ профиль «Проценты. Вклады и кредиты»

 на образовательной платформе Учи.ру