Задачи к экзамены по дисциплине "Дискретная математика"

1        Даны отрезки А = [-4; 5], B = [2; 6], C = [5; 10]. Найдите следующее множество и изобразите его кругами Эйлера:

2        Даны отрезки А = [-7; 3], B = [1; 5], C = [4; 10]. Найдите следующие множества и изобразите их кругами Эйлера: ;

3        Даны отрезки А = [-2; 4], B = [2; 6], C = [5; 10]. Найдите следующие множества и изобразите их кругами Эйлера: ;

4        Выполните действия и определите мощность полученного множества

5        Выполните действия и определите мощность полученного множества

6        В=

7        По заданной функции постройте таблицу истинности, приведите функцию к минимальной ДНФ:
 

8        Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X → (Y ≡ Z) и F2 = (X → Y) ≡ (X → Z)

9        Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X ∙ (Y ≡ Z) и F2 = (XY) ≡ (XZ);

10    Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X → (Y Ú Z) и F2 = (X → Y) Ú (X → Z);

11    Используя законы алгебры логики доказать справедливость Закона склеивания относительно дизъюнкции и конъюнкции:    и     .

12    Доказать с помощью таблиц истинности справедливость закона де Моргана относительно операций конъюнкции и дизъюнкции.

13    Проверьте, являются ли булевы функции F₁ и F₂  эквивалентными, если  и .

14    Проверьте, являются ли булевы функции F₁ и F₂  эквивалентными, если  и .

15    Вычислите значение функции F(x₁, x₂, x₃) при заданных значениях аргументов
 x₁ = 0, x₂ = 1, x₃ = 1 и при  x₁ = 0, x₂ = 0, x₃ = 1:
F(x₁, x₂, x₃) =

16    Докажите или опровергните:

17    Построить таблицу истинности для следующей формулы: A & (B Ú Þ )

18    Построить таблицы истинности алгебраически для следующей формулы: A Ú (B Ú Þ) 

19    По заданной функции постройте таблицу истинности, приведите функцию к минимальной ДНФ:
 F(x₁,x₂,x₃) =

20    Вычислите значение функции F(x₁, x₂, x₃) при заданных значениях аргументов x₁ = 1, x₂ = 0,
x₃ = 1 и при x₁ = 1, x₂ = 0, x₃ = 1:   F(x₁,x₂,x₃) =

21    Вычислите значение функции F(x₁, x₂, x₃) при заданных значениях аргументов x₁ = 0, x₂ = 0,
x₃ = 1 и при x₁ = 0, x₂ = 1, x₃ = 1: F(x₁,x₂,x₃) =

22    Упростите функцию, приведя ее к минимальной ДНФ: F(x₁,x₂,x₃) =

23    Упростите функцию, приведя ее к минимальной ДНФ:  F(x₁,x₂,x₃) =

24    Упростите функцию, приведя ее к минимальной ДНФ:  F(x₁,x₂,x₃) =

25    Постройте логическое выражение по заданной таблице истинности, приведите его к минимальной ДНФ алгебраически:

26    Постройте логическое выражение по заданной таблице истинности, приведите его к минимальной ДНФ алгебраически:

27    Минимизируйте булеву функцию с помощью карт Карно или диаграмм Вейча:

28    Минимизируйте булеву функцию с помощью карт Карно или диаграмм Вейча:

29    Постройте совершенные ДНФ и соответствующие минимальные формы для булевых функций, заданных таблично, с помощью карт Карно. Постройте соответствующий логический элемент.

30    Постройте совершенную ДНФ по таблице истинности и преобразуйте ее в полином Жегалкина:

31 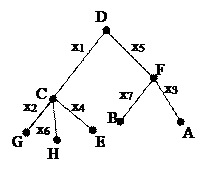   Определите по рисунку справа вид графа, степени его вершин. Имеет ли граф висячие вершины?

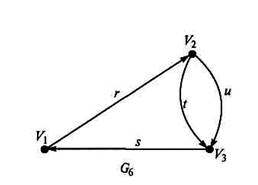
32    Определите по рисунку слева вид графа и постройте таблицы инцидентности и смежности