
Задачи на вычисление расстояния от точки до плоскости и на теорему о трех перпендикулярах.
Справочный материал на формулы площадей и на радиусы описанной и вписанной окружности.
R – радиус описанной окружности; r – радиус вписанной окружности.
1. Треугольники.
Разносторонний (стороны a, b, c).
S = ![]() p=
p= 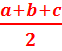
R= ![]() ; r =
; r = ![]() .
.
Прямоугольный (a и b – катеты, с – гипотенуза).
S = ![]() ;
; ![]() =
= ![]() ; r =
; r =  .
.
Равносторонний (а – сторона)
S = 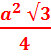 ; R =
; R = ![]() ; r =
; r = ![]() ; R = 2r.
; R = 2r.
2 .Квадрат ( а – сторона).
S = a2 ; R= 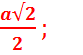 r =
r = ![]() .
.
3.Прямоугольник ( a и b – смежные стороны , d –диагональ).
S = a· b ; R = ![]() ; d =
; d =![]() .
.
4. Правильный шестиугольник ( а – сторона).
S= 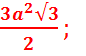 R = a; r =
R = a; r = ![]() .
.
Самостоятельная работа.
Вариант 1.
1. К плоскости окружности из ее центра восстановлен перпендикуляр, длина которого равна 8 см. Найдите расстояние от конца перпендикуляра до любой точки окружности, если радиус окружности равен 3см.
2.Из центра правильного треугольника восстановлен перпендикуляр к его плоскости. Сторона треугольника равна 4√3, а длина перпендикуляра равна 3. Найдите а) расстояние от конца перпендикуляра до вершин треугольника; б) расстояние от конца перпендикуляра до сторон треугольника (ответ округлить до десятых).
3.Из центра квадрата восстановлен перпендикуляр к его плоскости. Сторона квадрата равна 12, а длина перпендикуляра равна 4. Найдите а) расстояние от конца перпендикуляра до вершин квадрата; б) расстояние от конца перпендикуляра до сторон квадрата (ответ округлить до десятых).
4.Из центра треугольника с сторонами 10см, 10см и 16см
восстановлен перпендикуляр к его плоскости. Длина перпендикуляра равна 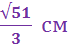 . Найдите а)
расстояние от конца перпендикуляра до вершин треугольника (ответ округлить до
десятых);
. Найдите а)
расстояние от конца перпендикуляра до вершин треугольника (ответ округлить до
десятых);
б) расстояние от конца перпендикуляра до сторон треугольника (ответ округлить до десятых).
5. Из центра прямоугольника восстановлен перпендикуляр к его плоскости. Стороны прямоугольника равны 12см и 16см, а длина перпендикуляра равна 15см. Найдите а) расстояние от конца перпендикуляра до вершин прямоугольника; б) расстояние от конца перпендикуляра до каждой стороны прямоугольника (ответ округлить до целого).
6. Из центра описанной окружности около прямоугольного треугольника восстановлен перпендикуляр к его плоскости. Катеты прямоугольного треугольника равны 2см и 2√3 см, а длина перпендикуляра равна 8√3 см. Найдите
а) расстояние от конца перпендикуляра до вершин треугольника;
б) радиус вписанной окружности в этот треугольник (ответ округлить до десятых).
7. Из центра правильного шестиугольника восстановлен перпендикуляр к его плоскости. Сторона шестиугольника равна 3, а длина перпендикуляра равна 4. Найдите а) расстояние от конца перпендикуляра до вершин шестиугольника; б) расстояние от конца перпендикуляра до сторон шестиугольника (ответ округлить до десятых).
Вариант 2.
1. К плоскости окружности из ее центра восстановлен перпендикуляр, длина которого равна 2,4 см. Найдите расстояние от конца перпендикуляра до любой точки окружности, если радиус окружности равен 1 см.
2.Из центра правильного треугольника восстановлен перпендикуляр к его плоскости. Сторона треугольника равна 3√3, а длина перпендикуляра равна 4. Найдите а) расстояние от конца перпендикуляра до вершин треугольника; б) расстояние от конца перпендикуляра до сторон треугольника (ответ округлить до десятых).
3.Из центра квадрата восстановлен перпендикуляр к его плоскости. Сторона квадрата равна 24, а длина перпендикуляра равна 5. Найдите
а) расстояние от конца перпендикуляра до вершин квадрата; (ответ округлить до десятых);
б) расстояние от конца перпендикуляра до сторон квадрата.
4.Из центра треугольника с сторонами 40см, 9см и 41см
восстановлен перпендикуляр к его плоскости. Длина перпендикуляра равна 3![]() . Найдите
а) расстояние от конца перпендикуляра до вершин треугольника (ответ округлить
до десятых);
. Найдите
а) расстояние от конца перпендикуляра до вершин треугольника (ответ округлить
до десятых);
б) расстояние от конца перпендикуляра до сторон треугольника.
5. Из центра прямоугольника восстановлен перпендикуляр к его плоскости. Стороны прямоугольника равны 12см и 16см, а длина перпендикуляра равна √69 см. Найдите а) расстояние от конца перпендикуляра до вершин прямоугольника; б) расстояние от конца перпендикуляра до каждой стороны прямоугольника (ответ округлить до целого).
6. Из центра описанной окружности около прямоугольного треугольника восстановлен перпендикуляр к его плоскости. Катеты прямоугольного треугольника равны 8см и 8√3 см, а длина перпендикуляра равна 6 см. Найдите
а) расстояние от конца перпендикуляра до вершин треугольника;
б) радиус вписанной окружности в этот треугольник (ответ округлить до десятых).
7. Из центра правильного шестиугольника восстановлен перпендикуляр к его плоскости. Сторона шестиугольника равна 3, а длина перпендикуляра равна 4. Найдите а) расстояние от конца перпендикуляра до вершин шестиугольника; б) расстояние от конца перпендикуляра до сторон шестиугольника (ответ округлить до десятых).
Ответы на задачи.
Вариант 1.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ответ |
10 |
а) 5; б) 3,6 |
а) 8; б) 7,1 |
а) 8,7; б) 3,6 |
а) 18; б)16; 17 |
а) 14; б) 0,7 |
а) 5; б) 4,8 |
Вариант 2.
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Ответ |
2,6 |
а) 5; б) 4,2 |
а) 17,7; б) 13 |
а) 20,7; б) 5 |
а) 13; б)12; 10 |
а) 10; б) 2,9 |
а) 17; б) 16,5 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.