01-05. Задачи с практическим содержанием 

ПРИМЕРЫ

«Листы бумаги»

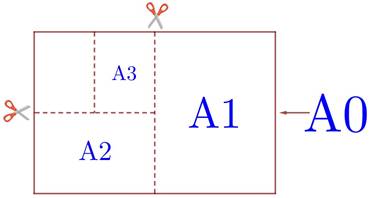Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2. И так далее. Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.

В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А2, А3 и А5.

1.  Установите соответствие между форматами и номерами листов бумаги из таблицы. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр.

Чем больше цифра формата, тем меньше длина листа.  Расставим длины листов в порядке убывания: 

 Ответ: 3241

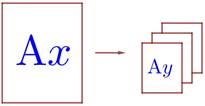
2.  Сколько листов формата А5 получится из одного листа формата А1?

                                                А3

А2 ФОРМУЛА

                                                              А3

А1 …                                                                                                       (y x₋ )

                                                                                          А3 =2

А2

                                                А3

Ответ: 16.

3.  Найдите ширину листа бумаги формата А4. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

4.  Найдите длину листа бумаги формата А1. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

Интересно! На самом деле длина листа формата А1 равна 841 мм, чтобы эта неточность не отразилась на правильности ответа, в задаче требуется округлить полученную длину до ближайшего целого числа, кратного 10.

5.  Найдите отношение длины большей стороны листа формата А6 к меньшей. Ответ округлите до десятых.

Ответ: 1,4.

6.  Найдите отношение длины диагонали листа формата А5 к его меньшей стороне. Ответ округлите до десятых.  

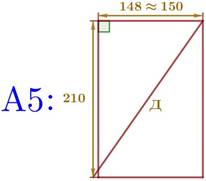Для упрощения вычислений  

длину/ширину листа можно округлить. По теореме Пифагора найдем длину диагонали:

                                                                                                      Д= 210 +150 66600 666 100 67610^{2                                                                                           2}=    =                                  =260

Меньшая сторона – это ширина листа, для формата А5: 150 мм.

                                               Д 260    26

Отношение:       =              1,731,7.

                                              М 150    15

Ответ: 1,7.

Интересно! Так как ответ во всех заданиях такого типа необходимо будет округлить до десятых, для упрощения вычислений округлите длины сторон до числа кратного 10 (1200; 850; 600; 300; 150) или 5 (105; 75). На правильности ответа это не отразится. Также для упрощения вычислений можно учесть тот факт, что все листы подобны и все отношения (большая сторона к меньшей, меньшая к большей, диагональ к меньшей/большей стороне) будут одинаковыми для всех форматов (1,4/0,7/1,7/1,2).

7. Найдите площадь листа формата А3. Ответ дайте в квадратных сантиметрах.

SлфA0 =1 м2=10 000 см2                                       SлфA0                                 2

1 лф А0  2 лф А1  4 лф А2 =       =                     = 8 лф А3           S_лфA3 = 8 = 8   = 1 250 (см )

Ответ: 1250.

8.          Бумагу формата А2 упаковали в пачки по 120 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 180 г. Ответ дайте в граммах.

                                                                                                                                                                                 4     180

S_лфA0 =1 м²  m_лфA0 =180 г       4 листа 180 г−  120 ^{= x} 1 лф А0  2 лф А1 = = 4 лф А2 120 листов − x г _{x = =5400 ( г)}

Ответ: 5400

9.          Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, то есть 0,3528 мм. Текст напечатан шрифтом высотой 20 пунктов на листе формата А2. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 таким же образом? Размер шрифта округляется до целого.

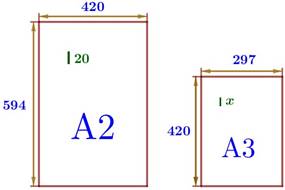Так как листы подобны, то отношение высот шрифтов будет таким же, как отношение длины (ширины) листов двух рассматриваемых форматов.  

Можно составить пропорцию как относительно длины, так и ширины:  

                                                                                                                       20   594         20 420

1)     =  x =  14,1414 x 420 594

                                                                                                             20   420         20 297

2)     =  x =  14,1414 x 297 420

Ответ: 14.

Интересно! Для увеличения шрифта можно использовать коэффициент 1,4, для уменьшения – 0,7. Проверяем: 200,7=14 и 141,4=19,620.