Задания для самостоятельной работы ученика

Урок по теме «Векторный и координатный  методы решения задач»

Автор: Попченко Светлана Николаевна, учитель математики МБОУ СОШ №3 г.Клинцы Брянской обл.

 Описание: конспект  урока «Векторный и координатный  методы решения задач», составлен в соответствии с ФГОС второго поколения, будет полезен учителям математики общеобразовательных школ при прохождении данной темы. 

Тип урока: обобщения и систематизации.

Формы проведения урока: индивидуальная, в группах.

Цели урока:

Учебные:                                                                                                               

Ø -учить использовать отдельные компоненты векторного и координатного методов;                                                                  получение алгоритма применения методов в целом

Развивающие:

Ø формирование умений выполнять обобщение и конкретизацию                                                                                                       - активизировать познавательную деятельность учащихся через                                                                                - развивать логическое мышление;                                                                                     - развивать умения анализировать и делать выводы.

Ø Воспитательные:                                                                                                               - воспитывать у учащихся интерес к предмету, доброжелательность;                - воспитывать стремление к совершенствованию знаний.

- Регулятивные УУД: умение  оценивать правильность выполнения действия на уровне адекватной  оценки; проговаривать последовательность действий на уроке; планировать своё действие в соответствии с поставленной задачей;  вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.

- Коммуникативные УУД:  умение оформлять свои мысли в устной форме; слушать и понимать речь других.

- Познавательные УУД: добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

Оборудование:

учебник, таблицы, доска, набор геометрических тел, мультимедийный проектор, экран, компьютер, презентация.

          Над доской высказывание:

«Сущность геометрии в её методе, где строгость вывода соединяется с наглядными представлениями» А.Д. Александров

Ход урока:

1.Организационный  момент

Организация учащихся к работе на уроке.

2. Проверка домашнего задания

(Домашнее задание содержит разные задачи, но общее у них – применение векторов и координат к их решению).

      Для первой группы:

Определите вид четырёхугольника АВСD, если А(-1; 2; -3), В(-5; 2; 1), С(-9; 6; 1), D(-9; 10; -3).

      Для второй группы:

Даны точки А(3; 1; 5) и В(-2; 2; 4). Найдите на оси аппликат все такие точки С, что треугольник АВС – равнобедренный.

      Для третьей группы:

Найдите четвёртую вершину правильного тетраэдра РАВС, если А(0; 0; 4), В(0; 4; 0), С(4; 0; 0).

3. Подготовка учеников к активному и осмысленному усвоению учебного материала (Цель: проверка овладением понятийным аппаратом, основными действиями).

1.)Математический диктант

а) Координаты .

б) А(-3; 0; 0). Укажите, где расположена эта точка.

в)  Запишите координаты вектора .

г) . Укажите взаимное расположение и .

д) ={-1; 0; 1}. Разложите по базисам .

е) Сформулируйте определение скалярного произведения векторов и.

ж) М(х; у; z). Разложите вектор по базису .

з) Где находится точка К(5; 0; -3)?

и) Границы угла между векторами.

к) Координаты середины отрезка по координатам его концов.

2.)Заполнение пропусков в таблице с теоретическими сведениями

(каждая группа заполняет свою часть таблицы и готовит вопросы для других групп).

1) а)+        =   ,

 =    -      ,

+      =;

			↓↓.

б) и- коллинеарные, значит  =

2.) а) если и- неколлинеарные, то  , если    ;

     б) если и, - некомпланарные, то    .

3)    а)  · =

  ;

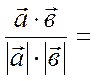б) если , то         ;

если  ·  >0, то     ;

если угол ( ,) – тупой, то   ; =   =   .

Подведение итогов.

Какие строчки заполнялись без затруднений?

Какой вопрос самый интересный?

Кто задал самый интересный вопрос?

4.Постановка познавательной задачи

(Цель: проверка сформированности действий перевода информации с координатного языка на векторный и обратно).

1.Нужно ли выбирать систему координат при решении задач векторным методом?

2.Что позволяет сделать при решении задачи удачный выбор системы координат?

3.Как выбирается система координат? Можно ли дать рекомендации по её выбору?

4.Нужно ли выбирать систему координат, если задача звучит так:

а) Найдите угол между векторами ={1; 2} и ={-3; 1}.

б) Четыре точки заданы своими координатами А(3; 1), В(1; 4), С(1; 0) и

D(4; 5).Найдите угол между прямыми АВ и СD.

2.

(Каждая группа отвечает на вопросы по переводу информации на векторный и координатный язык).

5. Усвоение новых знаний и способов действий

Дополнительные задания (на распечатках)

1. 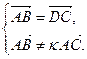Какую фигуру задаёт система?

2.Дано: ABCD – трапеция с основаниями АС и ВD, АС >ВD. Запишите это утверждение в векторной форме.

Каждой группе предлагается задача.

Не решая задачу, покажите, какая система координат наиболее целесообразна для поиска решения данной задачи. Для этого целесообразно использовать модели,  можно выполнить чертежи на альбомных листках и сделать выставку. Решите задачу двумя методами.

Для 1-й группы:

          Докажите, что диагонали ромба взаимно перпендикулярны, используя векторы.

Для 2-й группы:

В тетраэдре РАВС рёбра АР и ВС, а также АВ и СР взаимно перпендикулярны. Докажите перпендикулярность рёбер АС и ВР, используя векторы.

Для 3 –й группы:

Все рёбра правильной четырёхугольной пирамиды РАВСD имеют длину, равную 1. Найдите угол между векторами , где точки М и К – середины рёбер соответственно ВС и СР.

6.Первичная проверка понимания и коррекция усвоения учениками нового материала

(Представитель каждой группы объясняет выбор системы координат).

Как вы думаете, какова цель этого этапа?

        После выступления групп составляется алгоритм действия по применению векторного и координатного  методов решения задач ( затем раздать алгоритм  в распечатках учащимся).

      Основные компоненты векторного метода решения задач

1.     Перевод условия задачи на язык векторов:

       - выбор системы координат (если это необходимо);

       -выбор базисных векторов;

       -разложение всех введенных векторов по базисным.

2.Составление векторного равенства (или системы равенств).

3.Упрощение векторных равенств или замена их алгебраическими уравнениями (или системой уравнений) и их решение.

4.Объяснение геометрического смысла полученного результата.

Основные компоненты координатного  метода решения задач

      1.Выбрать систему координат.

      2.Найти координаты нужных точек, векторов или составить уравнения

         нужных фигур.

      3.Сформулировать задачу с помощью координат, решить её и сделать

         вывод без использования координат.

7. Закрепление знаний и способов действий, самопроверка знаний

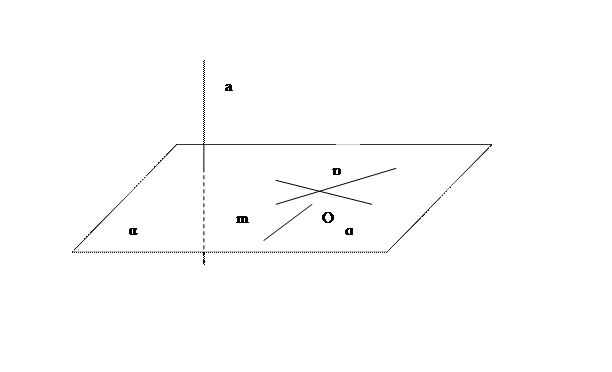
Доказать признак перпендикулярности прямой и плоскости векторным методом.(Запись на доске)

Дано:

ар, аq; р пересекает q в точке О; р и q лежат в плоскости α.

Доказать:

а α(то есть доказать, что аm, где m – произвольная прямая плоскости α).

Доказательство:

1.     Перевод условия и заключения теоремы на векторный язык.

 - направляющие векторы прямых.

Дано:

принадлежат α; принадлежит α.

Доказать:

.

Доказательство:

1) ↔=0.

2) ↔=0.

3) ↔→ аm→ а α, что и требовалось доказать.

8. Рефлексия

1) оценка за урок у каждого ученика на листе с диктантом;

2) собственная оценка за работу на уроке.

1.Кто себе поставил «5»?

2.Какой момент наиболее интересен был на уроке?

Где пришлось более всего концентрироваться, вдумываться?

9. Информация о домашнем задании

1.Найти и решить задачи (2-3), где прослеживается применение векторного и координатного аппарата в физике, технике, химии, лингвистике.