Зеркальные магнитные ловушки: принцип действия.

Зеркальные магнитные ловушки: принцип действия.

Одним из возможных подходов к решению проблемы УТС являются ловушки  с магнитными пробками или адиабатические либо открытые ловушки.

Хотя ловушки подобного типа были предложены еще на заре термоядерных исследований (в 1952 году Будкером в СССР и независимо Йорком и Постом в США)‚ после 35 лет экспериментов они не оказались отвергнутыми и продолжают сохранять шансы послужить основой для термоядерного реактора. Более простые в техническом отношении‚ они явились удобным стендом испытаний по УТС‚ первые успехи по кинетическим и МГД - неустойчивостям. В настоящее время‚ благодаря своим способностям удерживать плазму с давлением‚ сравнимым с давлением магнитного поля‚ появлению новых идей по улучшению удержания‚ адиабатические ловушки продолжают оставаться основным конкурентом тороидальных систем в термоядерной гонке‚ обещая более простой технически и выгодный экономически термоядерный реактор.

Принцип заключается в том‚ что плазма создается не в виде тора (как в токамаках и стеллараторах)‚ а в виде прямого цилиндра‚ помещенного в цилиндрически симметричное магнитное поле‚ усиливающееся на концах плазменного цилиндра. Магнитные силовые линии зеркальной ловушки имеют следующую конфигурацию (на рис. дано распределение напряженности магнитного поля).

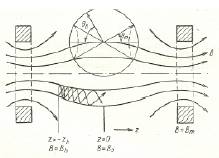
Рассмотрим поведение отдельных заряженных частиц в такой конфигурации магнитного поля. Раньше мы видели‚ что в магнитном поле частица движется по спирали радиуса

                                                                                    (5.1)

Шаг спирали определяется продольной скоростью V‚ которая не возмущается магнитным полем‚ если поле однородно.

Если же вдоль силовой линии‚ вокруг которой движется частица‚ силовые линии сгущаются (т.е. В нарастает)‚ то‚ как следует из анализа движения частицы в этих условиях‚ остается неизменной полная энергия частицы  и так называемый магнитный момент (т.е. поток через орбиту). Покажем‚ что магнитный момент сохраняется. Исходим из того‚ что‚ согласно электромагнитной индукции‚ магнитный поток через орбиту не изменяется. Тогда магнитный поток Ф=B×S=B×p

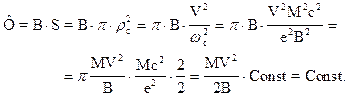
Следовательно‚ если Ф=Const‚ то .

Иными словами:

                 ‚                               (14.1)

                 ‚                                        (14.2)

где W - полная энергия частицы‚ а W  и W   - ее составляющие.

Формула (14.2) справедлива лишь в адиабатическом приближении‚ т.е. тогда‚ когда за время одного оборота частица не успевает сместиться вдоль силовой линии настолько‚ что В уже стало другим. Чтобы В заметно изменилось‚ частица должна сделать много оборотов - это и есть условие адиабатичности движения. Таким образом‚ магнитный момент является адиабатическим инвариантом движения частицы в слабо неоднородным магнитном поле.

Критерий адиабатичности определяется кривизной силовых линий и зависит от параметра:

                 ‚

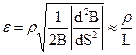где s - координата вдоль силовой линии.

Эксперименты и теория показывают‚ что e_крит»0‚04 и при e₀<0‚04 неадиабатические потери не опасны для термоядерного эксперимента.

Из (14.2) следует, что с ростом В растет W_┴=MV_┴²/2, но в силу (14.1) это ведет к уменьшению W_║=MV_║²/2. Иными словами, при вхождении в пробку частица притормаживается в продольном направлении, но ускоряется в поперечном направлении. Если В нарастает до достаточно больших значений, то W_┴  растет согласно (14.2) непрерывно, пока не исчерпает весь запас кинетической энергии частицы, т.е. пока W_║ не превратиться в нуль. Здесь частица остановится, торможение частицы осуществляется некоторой силой магнитного происхождения, обусловленной наличием градиента магнитного поля в осевом направлении (диамагнитная сила). В самом деле, из (14.1) следует, что полная энергия сохраняется, но если интересоваться продольным движением, т.е. считать W_║  кинетической энергией, то тогда формально W_┴  - есть потенциальная энергия и формула (14.1) есть просто закон сохранения механической энергии. Но сила есть

,                                                                  (14.3)

где U - потенциальная энергия. Поэтому в зеркальной ловушке сила есть

                 .                                                            (14.4)

Заменяя из (14.2) W =mВ, имеем

                        F=-m×dB/dz=-m×gradB                                               (14.5)

Сила F продолжает действовать на частицу и после остановки, причем против gradB, т.е. внутрь ловушки, поэтому после остановки она ускоряется внутрь ловушки. Иными словами, частица упруго отражается от зеркал и оказывается захваченной между ними. Однако, не все частицы окажутся захваченными, а только те, которые будут остановлены до максимума магнитного поля зеркала, т.к. в максимуме dB/dz=0 и F=0. Т.е. частицы, которые не остановятся при B=B_max, покинут ловушку. Посмотрим, что это за частицы. Пусть величина поля, формирующего ловушку, имеет такое пространственное распределение.

При z=0          W_┴=W_┴0;        W_║=W_║0.

При движении вдоль z совершается "работа" по торможению частицы. Мы берем слово работа в кавычки, т.к., собственно говоря, здесь идет речь не о совершении работы за счет внешних сил (поле В не совершает работы), а о перекачке продольной энергии в поперечную. Но внешне процесс идет так, как будто В работает, если считать W_┴ - потенциальной энергией (на самом деле, это тоже кинетическая энергия, но это так называемый метод аналогии).

                 dA=Fdz=-m×dB/dz×dz=-m×dB                                                (14.6)

Эта работа приводит к уменьшению продольной энергии

                 dW_║=dA=-m×dB  (т.к. m=W_║/B, т.е. W_║=mB; dW_║=mdB)   (14.7)

Значит, при движении к пробке продольная энергия

W_║=-mקdB+C=-m×(B-B_min)+C                                             (14.8)

При В=Вmin (z=0); W_║=W_║0 и, значит, C=W_║0. Итак:

                 W_║=W_║0-m×(B-Bmin) (W_║ не может быть <0)                    (14.9)

Эта формула показывает, как тормозится вдоль z частица. Из (14.9) видно, что частица будет захвачена, если

                 W_║0<m×(Bmax-Bmin)                                                            (14.10)

и уйдет из ловушки, т.е. будет пролетной, если

                 W_║0>m×(Bmax-Bmin)                                                            (14.11)

Критерий для захваченных частиц можно записать удобнее. Сделаем это:

или

                 ‚                                                                        (14.12)

                 .                                                            (14.13)

Левая часть критерия характеризует угол наклона скорости частицы V к оси z в центре ловушки q:

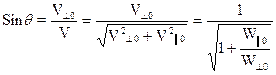                 .                         (14.14)

Отсюда

                 .                                                                 (14.15)

Подставим (14.15) в критерий (14.12)

     ‚       откуда 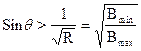.           (14.16)

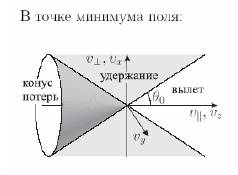
Итак, частица будет захвачена зеркальной ловушкой, если вектор ее скорости в центре ловушки лежит вне конуса с углом раствора q₀, этот конус называется конусом потерь или запретным конусом.

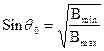                 .                                                                    (14.17)

Таким образом, если в зеркальную ловушку запущена частица, удовлетворяющая критерию (14.16), то она будет оставаться в ловушке неограниченно долго, если, конечно, условие адиабатичности (плавность изменения магнитного поля в пространстве). Оказывается, что условие адиабатичности выполнимо, если за время пролета между пробками частица делает не менее 10 циклических оборотов.

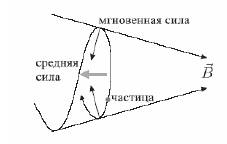
Вопрос о длительности сохранения адиабатического инварианта был исследован экспериментально в изящной работе Родионова (Арцимович, УТР, стр.47), которая состояла в следующем: измерялось время жизни b-частиц, образующихся при радиоактивном рампаде трития, удерживаемых в зеркальной ловушке. Измерения, выполненные в широком интервале изменения давления трития, показали, что частицы могут испытывать до 10⁷ отражений от магнитных зеркал. Отсюда следует важный вывод: при правильно построенной магнитной системе нарушения адиабатической инвариантности не могут привести к заметной утечке частиц из ловушки.