Методические рекомендации к уроку

Тема урока "Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной."

Цели обучения:

6.2.2.14

решать системы линейных неравенств с одной переменной;

Критерии оценивания

Учащиеся

 знают:

□     как решать системы линейных неравенств с одной переменной

□     как приводить неравенства с помощью алгебраических преобразований к неравенству вида kx > b, kx ≥ b, kx < b, kx ≤ b;

□     как записывать, используя математическую символику, ответы к решениям систем неравенств;

умеют

□     решать системы линейных неравенств с одной переменной

□     решать линейные неравенства видов kx > b, kx ≥ b, kx < b, kx ≤ b

□     изображать решения систем неравенств на координатной прямой;

□     использовать обозначения для записи числовых промежутков в ответах;

□     записывать решения систем неравенств в виде числового промежутка и записывать заданный числовой промежуток в виде неравенства;

Теоретический материал

Неравенства, образующие систему, объединяются фигурной скобкой.

- пример.

Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали

Алгоритм решения системы неравенств

1) Решаем каждое неравенство системы отдельно.

2) Находим пересечение числовых промежутков, являющихся решением системы неравенств, с помощью координатной прямой.

3) Записываем полученное решение в виде числового промежутка или неравенства.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Актуализация опорных знаний. Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 1. Каждый выполняет самостоятельно.

Приложение 1

Ответы:

После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.

Работа с классом. Используя основные знания и навыки по решению линейных неравенств, а также умении определять пересечение числовых промежутков, сделать ввод в тему урока.

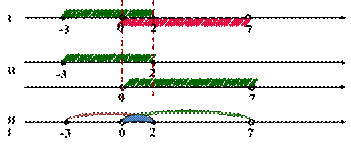
Задание: Найти пересечение множеств: [-3; 2]∩(0; 7)

.

Пересечение множеств: [-3; 2]∩(0; 7) может быть задано в виде:

Такую запись называют системой. Неравенства объединены фигурной скобкой, т.е это означает, что неравенства  и  - образуют систему, решением которой будет полуинтервал .

Решением системы является любое число из промежутка .

В тех случаях, когда нужно найти общее решение двух и более неравенств, говорят, что требуется решить систему неравенств.

Определение 1: Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.

Определение 2: Решить систему – значит найти все её решения или доказать, что решений нет.

Как решить полученную систему неравенств. Мы умеем решать отдельно неравенства, если решим их и найдем пересечение интервалов, тогда получим ответ.

1) Решить систему неравенств и указать целые решения.

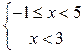
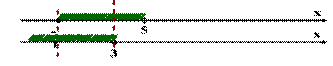
Ответ: [-1;3) - решение системы,

{-1;0;1;2}- целые решения.

2) Решить систему неравенств

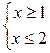
Ответ: [1;2]

Таким образом, учащиеся наметили несложный алгоритм решения системы неравенств с одной переменной:

1) Решаем каждое неравенство системы отдельно.

2) Находим пересечение числовых промежутков, являющихся решением неравенств системы, с помощью координатной прямой.

3) Записываем полученное решение в виде числового промежутка или неравенства.

Демонстрация презентации при наличии технических средств или схемы из Учебного пособия для учащихся Вассерман Ф.Я.

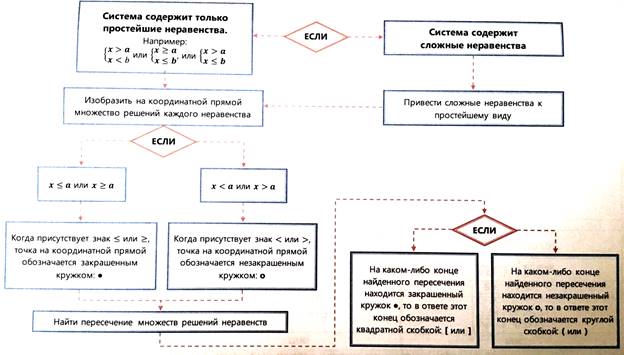
Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Рассмотрим примеры 1–3 Приложения 2 или из учебника. Это поможет увидеть различные варианты получаемых решений: интервалы, числовые лучи, пустое множество.

Первое и второе задания на отработку новых терминов и символики, а также на геометрическую интерпретацию решения систем неравенств. В третьем - будут задания на решение несложных систем неравенств.

Приложение 2

1) Является ли решением системы неравенств

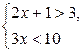 число 3? число 5?

2) Напишите решение системы неравенств в виде числового промежутка и изобразите его на координатной прямой:

Р е ш е н и е

а) 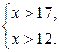           ;         (17; +∞); x > 17.

б) 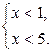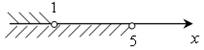;       (–∞; 1); х < 1.

в) 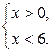;          (0; 6); 0 < x < 6.

г) 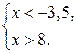       ;          ;                 нет решений.

д) 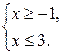          ;        [–1; 3];            –1 ≤ х ≤ 3.

е)             ;            (8; 20];            8 < x ≤ 20.

О т в е т: а) (17; +∞); б) (–∞; 1); в) (0; 6); г) нет решений; д) [–1; 3]; е) (8; 20].

3) Решите систему неравенств.

а)

Получили, что множество решений первого неравенства есть открытый числовой луч (4; +∞), а второго – (–∞; 5). Пересечение этих двух числовых промежутков и будет являться решением системы неравенств:

           (–∞; 5) (4; +∞) = (4; 5).

Решение можно записать как в виде числового промежутка, так и соответствующего ему неравенства: 4 < x < 5.

б)

            (–∞; –1); у < –1.

в)

            ; нет решений.

О т в е т: а) (4; 5); б) (–∞; –1); в) нет решений.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Вопросы   учащимся:

– Что называется решением системы неравенств?

– Что значит «решить систему неравенств»?

Вопросы для размышления:

•      Может ли система неравенств не иметь решений? Привести примеры.

•      Может ли система неравенств иметь одно решение? Привести примеры.

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Обязательное домашнее задание по цели обучения 6.2.2.14 по теме: «Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной» предполагает количество заданий, на выполнение которых учащиеся должны затрачивать не более 15-20 минут. Задания направлены на отработку навыков решения систем линейных неравенств. Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.        "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.    "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.       Вассерман Ф.Я. Математика 6 Учебное пособие для учащихся, изд БИС

Интернет ресурсы:

1.      http://www.yaklass.ru

2.      https://100ballov.kz

3.      https://mathematics.ru