10.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: 6.2.2.14 решать системы линейных неравенств с одной переменной Критерии оценивания:

- решают системы линейных неравенств с одной переменной

Организационный момент.      Для того чтобы перейти к изучению нового материала, необходимо вспомнить ранее изученный материал.

Этап обобщения и систематизации изученного.

а) Сопоставьте неравенство и его графическую иллюстрацию:

Ответ: 1- 1;          2-3;             3-1.

б) «Лови ошибку!»: «Математика учит преодолевать трудности и исправлять собственные ошибки». Найдите ошибку в решении неравенства, объясните почему допущена ошибка, запишите правильное решение.

Решить неравенства: (формирование познавательных УД)  

№1                                                №2
Решение:                                       

Учителю следует показать, как представлять решение системы неравенств, либо на числовой прямой, делая акцент на пересечение.

Как решали неравенства? (используя свойства.)

 Что же мы с вами уже знаем?

Перечислите свойства, используемые при решении?

 (- открывая скобки, знаки меняем на противоположные, если перед скобкой стоит знак минус;

-  перенося слагаемые из одной части в другу, меняем знаки;

- если обе части неравенства умножить или разделить на одно и то же число положительное то получится равносильное ему неравенство, если умножить или разделить на одно и тоже отрицательное число обе части уравнения, то знак неравенства нужно поменять на противоположный.)

3.Изучение новой темы.  Формулировка новой темы.

Показываю картинки с-мы (отопления, нервной системы, блок).

1.      Ребята, что показано на фотографиях? Что же их объединяет? Правильно, слово- система.

2. А какую тему мы изучали на прошлых уроках? (неравенства с одной переменной).

3. А что мы будем делать с системами?  (решать)

Итак, какая же тема нашего урока: Решение систем неравенств с одной переменной.   Открываем тетради, записываем число и тему урока.

Какова же цель нашего урока?

 Что мы хотим узнать? (Научиться решать простейшие системы, содержащие неравенства с одной переменной).

Проблемная задача.

ЗАДАЧА: Боковая сторона равнобедренного треугольника равна 18,6 см., а его периметр больше 42 см. Какую длину может иметь основание треугольника?

Что обозначим за х? (основание)

Каким условиям должен удовлетворять х?

1) 

Нужно найти значения х удовлетворяющие двум неравенствам, то есть решить систему неравенств.

Как нужно решать систему?

Решим каждое неравенство системы отдельно.

Проиллюстрируем решения каждого неравенства на одной числовой прямой

Какие же значения х будут решениями системы?

) (х принадлежащее интервалу).

Что назовем решением системы?    (Решением системы неравенств с одной переменной называется значение   переменной, при котором верно каждое из неравенств системы)

Что значит решить систему неравенств?      (Решить систему неравенств– значит найти все её решения или доказать, что решений нет)

Учащиеся должны определить, удовлетворяет ли решение двум неравенствам или только одному; и понять, что представляет собой изображение решения на числовой прямой.

Предложите учащимся составить алгоритм решения системы неравенств с одной переменной?  

1.Решить каждое неравенство системы.

2. Изобразить графически решения каждого неравенства на координатной прямой.

3. Найти пересечение решений неравенств на одной координатной прямой.

 4. Записать ответ в виде числового промежутка.

Дескриптор:

-выполняет действия с неравенствами;

-изображает на координатной прямой пересечение и объединение числовых промежутков;

-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

-находит решение системы неравенств.

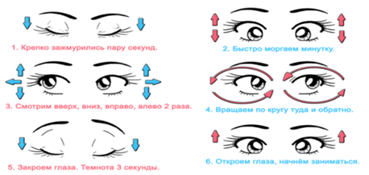
Проведите гимнастику для глаз.

Учащимся нужно дать задание для дальнейшего исследования неравенств через решение задач, представленных в устной форме. Они должны уметь принимать решения при выборе стратегий, методов и путей представления своих решений.

При реализации данной деятельности используется принцип дифференциации «Углубление», учащиеся проводят самостоятельное исследование и презентуют результаты. Данное задание может быть предложено для выполнения не всем учащимся, а например, учащимся с высоким уровнем математической подготовки.

Тренировочные упражнения. Учащимся предлагаются различные задачи для закрепления из учебного пособия. Дифференцированный подход осуществляет учитель (уровень B или C). Раздаточный материал должен содержат задачи с запасом на более способных учащихся с высокой скоростью решения.

Решение упражнений

1)                       3)

2)                    4)

Решение:

1) 

2) 

3) 

4) 

Дескриптор:

-выполняет действия с неравенствами;

-изображает на координатной прямой пересечение и объединение числовых промежутков;

-записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

-находит решение системы неравенств.

Домашняя работа:№1014 стр.232

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.