11. Методические рекомендации к проведению урока. Вариант 2.

Методические рекомендации к уроку

Тема урока: «Прямая пропорциональность и ее график».

Цели обучения:

Учащиеся:

6.5.2.12 записывать формулу прямой пропорциональности по описанию.

Критерии оценивания:

восстанавливает формулу прямой пропорциональности в соответствии с условием задачи.

Проверка домашней работы (сверяем ответы и комментируем решения, отвечаем на возникшие вопросы)

Тема урока, цели, критерии оценивания

 ( проговариваем, записываем тему урока в тетрадь).

Актуализация знаний:

Учитель раздаёт учащимся карточки и обращает внимание на слова Р Декарта:  «Для того, чтобы совершенствовать свой ум надо больше рассуждать, чем заучивать».

Учитель: - Хотелось бы, чтобы эти слова стали для нас руководством в  работе.

Задание №1 с математическими терминами, которые мы будем употреблять на уроке.

 Исправьте ошибки,  допущенные в написании этих терминов. (Слайды 5)

Поменяйтесь, листочками и проверьте, все ли ошибки исправлены? (Слайд 6)

Что вы заметили? В каком слове нет ошибок?

( график)

Вспомним материал прошлых уроков: работаем фронтально:

1. Какую зависимость называют  прямой пропорциональностью? (ответ: слайд 7).

2. Как называется число k? (ответ: слайд 7).

3.Какие из формул задают прямую пропорциональность? ( учащиеся перечисляют формулы прямой пропорциональности).

(Слайды 8 -9)

Задание №2 Выполняют задания  индивидуально на карточках.

Выразите зависимость ,  S-путь  t - время при скорости 50 км/ч.

Формула:­­­­­­­­­­­­­­___________________________

Заполните таблицу:

Постройте график  данной зависимости:

Задание№3.

Составьте формулы, для решения следующих задач.

1.  Дана  прямо пропорциональная  зависимость  , где Р- стоимость товара в рублях по цене 25 тенге. за килограмм, х- масса товара в килограммах.

Ответ: _______

2. Дана  прямо пропорциональная  зависимость  , где  S–площадь прямоугольника в м, со стороной a м и 6м.

Ответ:

3. Дана  прямо пропорциональная  зависимость  ,  где Р - периметр квадрата  в см, a – длина стороны  в см.

Ответ:

4. Дана  прямо пропорциональная  зависимость  , где C-длина окружности,  r-радиус этой окружности (3,14)

Ответ:

5. Какие  из предложенных зависимостей являются  прямо пропорциональными?

,   ,  ,   ,    у=х², ,,    

Прямая пропорциональность:_(выписать формулы, задающие прямую пропорциональность)

6.Придумай и запиши 4 формулы, задающие прямую пропорциональность:

1) ____ 2) ­­­____  3) ____ 4) ____

В парах производим взаимопроверку 9 заданий по формативному оцениванию на повторение. («+» за верно выполненное задание, «-» - задание выполнено неверно) Подводим итоги и сообщаем результаты (учитель фиксирует полученные результаты).

Работаем по группам: (4-5 человек) На столе лежат карточки разных цветов: красный, синий, зелёный. На этих карточках написаны пожелания: «Желаю тебе плодотворной работы», «Пусть твой сегодняшний урок пролетит на одном легком дыхании!», «Желаю, чтобы удача сопровождала тебя весь урок», «Пусть работа сегодня будет успешной» и т.д. Прочитав пожелания, учащиеся рассаживаются по цветам в три группы.

Каждая группа представляет свою работу на доске.  Отвечает на возникшие вопросы и оценивает другие группы по критериям (max 2 балла за каждый пункт, аргументировать, почему где – то баллы сняты, за что?)

·         задания решены без ошибок;

·         активное участие всех членов группы;

·         аккуратность оформления;

·         речь участников  группы математически грамотная.

1 группа

Уровень В

Задание 1

Даны точки 1), 2), 3)

а) Постройте график прямой пропорциональности, проходящей через точку А;

б) По графику  найдите значение k для каждой прямой;

в) для каждой прямой запишите формулу прямой пропорциональности.

1) Ответ: ;  2) Ответ: ;

   3) Ответ:

Уровень C

(Ответы на слайде 17)

Задание 2

На рисунке представлены графики отрезка АВ и луча СD

а) запишите уравнения прямых, на которых расположены отрезок и луч

б) укажите область определения и область значения зависимостей, представленных отрезком АВ и лучом CD

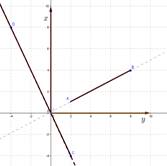
Ответ:

2 группа

Уровень В

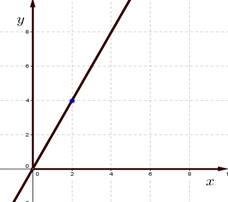
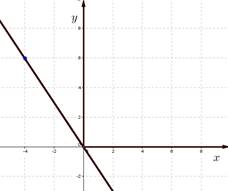
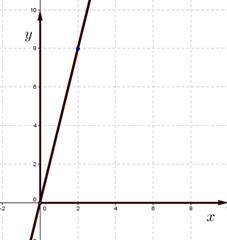
Задание 1. (Ответы на слайде 19)

а) По данным графикам запишите формулы зависимостей;

б) В каких координатных четвертях расположены графики данных зависимостей и почему?

Уровень С

Задание 2. (Слайд 20)

На рисунке  даны графики зависимостей. Фигура ограничена отрезками четырёх прямых. Запишите формулу каждой прямой.

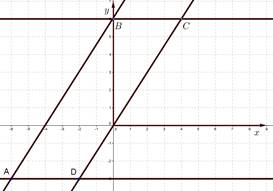
Почему коэффициенты у прямых (АВ) и (DC) – равны?

3.     Группа

Уровень В

Задание 1

Составьте формулу прямой пропорциональности, графиком которой является прямая АВ, проходящая через точку Е(-6;9)

Выберите правильный ответ.

А.   В.   С.      D.      

Решение:

Если  зависимость  представляет прямую пропорциональность, то .

 Ответ: B.

Учитель озвучивает оценки других групп, подводит итог работы и высказывает своё мнение о работе групп.

Рефлексия:

Возвращаемся к началу урока и на стикерах

(каждый критерий оценивания идёт под своим номером) оцениваем себя по критериям оценивания

Домашнее задание:

(если позволит время, то можно наиболее сложные задания, по мнению учащихся, разобрать устно)

Задание 1

Первый насос  заполняет бассейн за 4 часа, а второй насос – за 6 часов. Если будут работать вместе t часов, тогда  объём воды в бассейне будет . Запишите формулу зависимости  объёма  воды

() от времени t (ч) совместной работы двух насосов.

Задание 2

Запишите формулы зависимостей, графиками которых являются прямые  a,  b,  c.

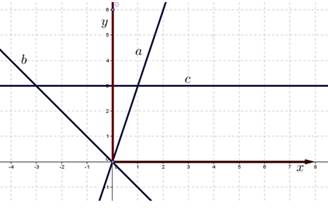Задание 3

Постройте прямую, параллельную графику   и проходящую через точку

1)    К(0;3);  2) О(0;0)

Решение:

Если прямая параллельна , то

k= -2. К(0;3)

Ответ: 1)  2)  

Дифференциация планируется по уровням заданий. Групповая работа планируется так, чтобы в одну группу попали учащиеся как сильные, так и слабые. Чтобы при работе совместной происходило  не только взаимное оценивание но и дополнительное обучение и взаимопомощь.

На уроке были задания разных уровней:

При повторении пройденного материала, в основном, уровень А. В групповой работе уровень В и С (задания на анализ и синтез). Так как это один из завершающих уроков по теме.

 Изучает рефлексию учащихся по критериям оценивания  для коррекции  планирования последующих уроков.

предполагают смену обстановки,  следовательно  физическую  и умственную разгрузку.

Список полезных ссылок и литературы

1.     Математика. 6 класс. – Т. А. Алдамуратова, Т. С. Байшоланов. – Алматы: «Атамұра», 2011.

2.     Математика. 6 класс. Часть 2. –

 Г. В. Дорофеев, Л. Г. Петерсон. – Москва: «Ювента», 2010.

3. https://vk-cc.com/G1NmjFy4

4. https://vk-cc.com/GkoeBi2t

Скачано с www.znanio.ru