Добавить материал

и получить 10 документов
и свидетельство автора

Рыбинок Екатерина Валерьевна

11. Системы линейных Методические рекомендации к уроку

docx
28.04.2020

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

11. Системы линейных Методические рекомендации к уроку.docx

Методические рекомендации к уроку

Тема урока "Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной."

Цели обучения:

6.2.2.14

решать системы линейных неравенств с одной переменной;

Критерии оценивания

Учащиеся

знают:

□ как решать системы линейных неравенств с одной переменной

□ как приводить неравенства с помощью алгебраических преобразований к неравенству вида kx > b, kx ≥ b, kx < b, kx ≤ b;

□ как записывать, используя математическую символику, ответы к решениям систем неравенств;

умеют

□ решать системы линейных неравенств с одной переменной

□ решать линейные неравенства видов kx > b, kx ≥ b, kx < b, kx ≤ b

□ изображать решения систем неравенств на координатной прямой;

□ использовать обозначения для записи числовых промежутков в ответах;

□ записывать решения систем неравенств в виде числового промежутка и записывать заданный числовой промежуток в виде неравенства;

Теоретический материал

Системы линейных неравенств с одной переменной с помощью тождественных преобразований сводятся к системе из простейших неравенств.

Если обе части неравенства разделить на отрицательное число, знак неравенства изменяется на противоположный, на положительное число - знак неравенства не изменяется

Ход урока

Организационный момент.

Проверить домашнее задание.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Актуализация опорных знаний. Индивидуальная работа. Для повторения и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 1. Каждый выполняет самостоятельно.

Приложение 1

Вариант 1.

Решить неравенства:

1. 9x<63;

2. –6x≤33;

3. >5;

4. 2(1+3x)>5+7x;

5. –6(2x–1) –(2+x)≥0.

Вариант 2.

Решить неравенства:

1. 8x<64;

2. –18x≤–27;

3. >3;

4. –3(x+2)>4–x;

5. –4(3–x) –2(3+x)≥0.

Ответы:

Вариант 1.

Решить неравенства:

1. (-;

2. [-5.5;;

3. (35;;

4. (-;-3)

5. (-.

Вариант 2.

Решить неравенства:

1. (-;

2. [1.5;

3. (18;;

4. (-;

5. [9;

После окончания выполнения, попросить обменяться учащихся тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать задания, которые были сделаны с ошибками.

Работа с классом. Урок углубления темы. Рассмотрим на примерах, как решить систему линейных неравенств.

Приложение 2.

Задание 1

$\left\{ \begin{array}{l} 3x - 4x \ge 4 - 5\\ 4x < 12 \end{array} \right.$ 2) $1)\left\{ \begin{array}{l} 7x - 12 \ge 3x - 20\\ 5 - 2x > 4x + 29 \end{array} \right.$

Пригласите к доске ученика, попросите его записать подробное решение задания. 1) $\left\{ \begin{array}{l} 3x - 4x \ge 4 - 5\\ 4x < 12 \end{array} \right.$

Обе части неравенства делим на число, стоящее перед иксом. В первом неравенстве делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Во втором — делим на положительное число, знак неравенства не изменяется:

$\left\{ \begin{array}{l} - x \ge - 1\_\_\_\left| {:( - 1) < 0} \right.\\ 4x < 12\_\_\_\left| {:3 > 0} \right. \end{array} \right.$

$\left\{ \begin{array}{l} x \le 1\\ x < 3 \end{array} \right.$

Оба неравенства со знаком «меньше» (не существенно, что один знак — строго «меньше», другой — нестрогий, «меньше либо равно»). Можем не отмечать оба решения, а воспользоваться правилом «меньше меньшего, больше большего«. Меньшим является 1, следовательно, система сводится к неравенству

$x \le 1$

Ответ: x∈(-∞;1].

Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске, внимательно слушают одноклассников. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого задания, акцентируйте их внимание на обоснование решений.

Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса.

Повторим, что системы линейных неравенств с одной переменной с помощью тождественных преобразований сводятся к системе из простейших неравенств.

Задание 2

$1)\left\{ \begin{array}{l} 7x - 12 \ge 3x - 20\\ 5 - 2x > 4x + 29 \end{array} \right.$

Чтобы решить систему, нужно решить каждое из составляющих её неравенств. Только решение принято записывать не по отдельности, а вместе, объединяя их фигурной скобкой.

В каждом из неравенств системы неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:

$\left\{ \begin{array}{l} 7x - 3x \ge - 20 + 12\\ - 2x - 4x > - 19 - 5 \end{array} \right.$

После упрощения обе части неравенства надо разделить на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не изменяется. Второе неравенство делим на отрицательное число, поэтому знак неравенства надо изменить на противоположный:

$\left\{ \begin{array}{l} 4x \ge - 8\_\_\_\left| {:4 > 0} \right.\\ - 6x > - 24\_\_\_\left| {:( - 6) < 0} \right. \end{array} \right.$

$\left\{ \begin{array}{l} x \ge - 2\\ x < 4 \end{array} \right.$

Решение неравенств отмечаем на числовых прямых:

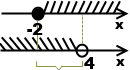
В ответ записываем пересечение решений, то есть ту часть, где штриховка есть на обеих прямых.

Ответ: x∈[-2;1).

Решение следующих систем неравенств в зависимости от уровня обучаемости класса. Часть можно дать для самостоятельного решения или как домашнее задание. Напомнить правило правильного раскрытия скобок. Можно раздать такие памятки.

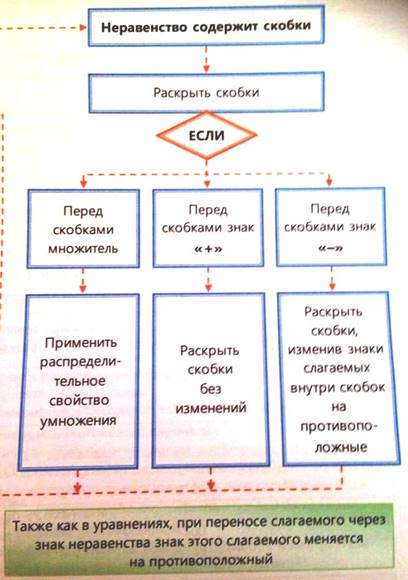
Уровень В Уровень С

Ответы:

1.2.	(–2;6]	1.3.	Нет решений
2.2.	[6;+∞)	2.3.	(–4; –2]
3.2.	(–4;6)	3.3.	(0;0,6)
4.2.	[4; +∞)	4.3.	(–4; –1]
5.2.	(–∞;3,5]	5.3.	[1,5;+ ∞)
6.2.	[1,5;4)	6.3.	Нет решения

При наличии компьютера, просмотреть презентацию для визуального закрепления материала. Дальнейшее закрепление провести в парах.

Работа в парах. Взаимное обучение.

Создать пары из представителей разных групп. Предложить ученикам процесс взаимного обучения: объяснить напарнику ход решения задания, затем вместе решить их. Определяем умение распределять обязанности в паре.

Предоставить достаточно времени для выполнения задания.

Приложение 3

В а р и а н т 1

Решить систему неравенств:

1. 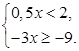2.

В а р и а н т 2

Решить систему неравенств:

1. 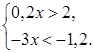2.

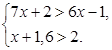
Подвести итог после решения этих заданий.

Индивидуальная работа. Решить из учебного пособия аналогичные примеры, провести формативное оценивание.

Беседа. Рефлексия.

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

радуга успеха.jpg

Домашнее задание. Обязательное домашнее задание по цели обучения 6.2.2.14 по теме: «Системы линейных неравенств с одной переменной. Решение системы линейных неравенств с одной переменной» предполагает количество заданий, на выполнение которых учащиеся должны затрачивать не более 15-20 минут. Задания направлены на отработку навыков решения систем линейных неравенств. Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1. "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2. "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4. Вассерман Ф.Я. Математика 6 Учебное пособие для учащихся, изд БИС

Интернет ресурсы:

1. http://www.yaklass.ru

2. https://100ballov.kz

3. https://mathematics.ru

Скачано с www.znanio.ru

Второе неравенство делим на отрицательное число, поэтому знак неравенства надо изменить на противоположный:

Домашнее задание. Обязательное домашнее задание по цели обучения 6

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также