13.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: 6.2.2.14 решать системы линейных неравенств с одной переменной Критерии оценивания:

- решают системы линейных неравенств с одной переменной

Организационный момент.     

Для того чтобы перейти к изучению нового материала, необходимо вспомнить ранее изученный материал.

Актуализация учебных знаний.

Для актуализации данного этапа урока предложите учащимся приемом «Корзина идей». Для этого объедините учащихся в 3-4 группы и раздайте каждой группе стикеры. На стикерах учащиеся пишут все, что они знают по изучаемой теме. Спроецируйте на интерактивной доске рисунок корзины (если нет такой возможности, то нарисуйте на доске). После заполнения стикеров, учащиеся клеят их на корзину, тем самым собирают все то, что они знают об изучаемой теме.

Тестовая работа на проверку усвоения цели обучения. На данном этапе у учащихся развивается такая ценность академическая честность.

С помощью этого теста можно проверить теоретические и практические знания по теме: «Системы линейных неравенств с одной переменной.»

После окончания работы проверить по готовым ответам на слайде и обсудить ошибки.

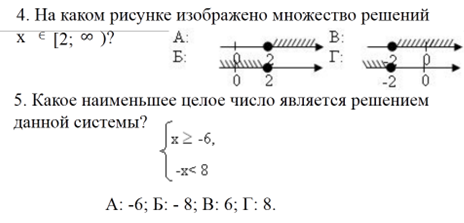
Ключ к тесту: 1. Г   2. Б      3.В     4. А   5. А

Проведите гимнастику для глаз.

Разделите учащихся по парам в зависимости от уровня способностей на базовый, средний и продвинутый.

Предложите учащимся самим выбрать задания в зависимости от уровня сложности.

На этом этапе у учащихся развивается уважение друг к другу и академическая честность.

Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а так же с учетом скорости мышления и возрастных особенностей учащихся.

Учащиеся проводят самооценивание своих решении, затем проводят проверку по готовым ответам. Учитель наблюдает за работой учащихся, в случае необходимости оказывая им поддержку.

Базовый уровень: Найти   все   решения     системы   неравенств и записать ответ с помощью числового промежутка:

Ответ:

1.полуинтервал [- 3,7; 5,1)

2.полуинтервал  (3; 7,9]

3.отрезок [-3,5; 2,7]

4. луч (3; + ∞)

5. луч (- ∞; - 3,1]

Средний уровень: Решите систему неравенств:

Решение. 1) решим каждое неравенство исходной системы, получим:

Изобразим решение неравенств на одной координатной прямой:

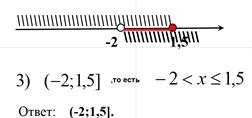
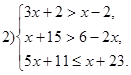
Решение. 1) Решим каждое из неравенств данной системы одновременно, получим:

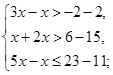
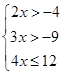
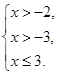
Изобразим решение неравенств на одной координатной прямой:

Продвинутый уровень:

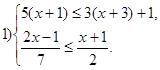
Решение. 1)  Решим каждое неравенство данной системы:

2)      Изобразим решение каждого из получившихся неравенств на одной числовой прямой:

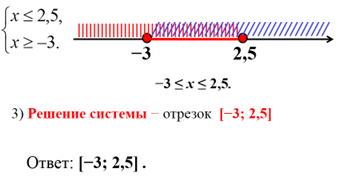
2) Задача. Одна сторона треугольника равна 5 метрам, а другая - 8 метрам. Какой может быть третья сторона, если периметр треугольника больше 17 метров?

Решение.  Пусть x метров (x>0) — длина третьей стороны треугольника, тогда, согласно условию задачи и учитывая неравенство треугольника, составим и решим систему неравенств:

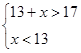
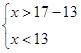
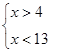
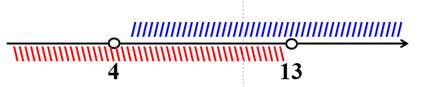
, значит, длина третьей стороны есть любое число из интервала

Ответ: длина третьей стороны больше 4 метров, но меньше 13 метров.

Дескриптор:

           -выполняет действия с неравенствами;

           -изображает на координатной прямой пересечение и объединение числовых промежутков;

           -записывает решения неравенств в виде числового промежутка и записывает числовой промежуток в виде неравенства;

           -находит решение системы неравенств.

Рефлексия.

Подведение итогов урока. Рефлексия.

Рефлексия. Учащиеся дополняют следующие предложение:

Сегодня на уроке я научился…

Сегодня на уроке мне понравилось…

Сегодня на уроке я повторил…

Сегодня на уроке я закрепил…

Сегодня на уроке я поставил себе оценку …

Домашняя работа.

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова. Алматы. Атамура. 2011 год.