1.4. Биссектрисса, высота, медиана треугольника

Биссектриса, высота, медиана треугольника.

Повторяем теорию.

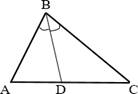
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

BD – биссектриса треугольника ABC,∠𝐴𝐵𝐷 = ∠𝐶𝐵𝐷.

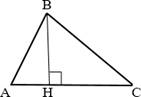Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

BH – высота треугольника ABC, 𝐵𝐻 ⊥ 𝐴𝐶.

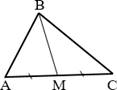Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

BM – медиана треугольника ABC, AM=MC.

Любой треугольник имеет три биссектрисы, три высоты и три медианы. Биссектрисы треугольника пересекаются в одной точке.

Медианы треугольника пересекаются в одной точке.

Высоты треугольника или их продолжения пересекаются в одной точке.

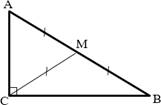Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Δ𝐴𝐵𝐶 – прямоугольный, CM – медиана, тогда 𝐶𝑀 =

¹ 𝐴𝐵.

2

Проверяем себя.

Т1. Закончите предложение.

Высота треугольника - это                    

а) отрезок, перпендикулярный стороне треугольника;

б) перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону

в)   отрезок,   соединяющий   вершину   треугольника   с              противолежащей стороной под прямым углом

Ответ: б).

Т2. Укажите верные утверждения:

а) каждая из биссектрис равнобедренного треугольника является его высотой;

б) биссектриса треугольника делит пополам сторону, к которой проведена; в) в любом треугольнике медианы пересекаются в одной точке.

Ответ: в).

Т3. Выберите неверные утверждения:

а) каждая из биссектрис равнобедренного треугольника является его медианой;

б) медиана треугольника делит пополам угол, из вершины которого проведена;

в)     отрезок,     соединяющий    вершину    треугольника     с               серединой противолежащей стороны треугольника, называется медианой.

Ответ: а), б).

Решаем задачи

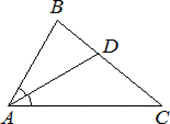
1.                        а)  В  треугольнике  ABC  известно,  что

∠BAC=62°, AD – биссектриса. Найдите угол BAD. Ответ дайте в градусах.

Ответ: 31

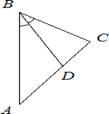б) В треугольнике ABC известно, что ∠BAD=36°, AD – биссектриса. Найдите угол BAС. Ответ дайте в градусах.

Ответ: 72

в) В треугольнике ABC известно, что ∠ABC=62°, ВD – биссектриса. Найдите угол ABD. Ответ дайте в градусах.

Ответ: 31

2. 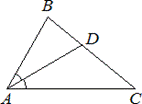                       а)    В     треугольнике    ABC    известно,    что

∠BAС=86°, AD – биссектриса. Найдите угол ADС, если

∠BСA=23°. Ответ дайте в градусах.

Ответ: 114

б) В треугольнике ABC известно, что ∠DAС=34°, AD – биссектриса. Найдите угол AСB, если ∠DBA=43°. Ответ дайте в градусах.

Ответ: 69

в) В треугольнике АВС угол С равен 50°, угол В равен 70°. Найдите угол

ВАD, если АD – биссектриса угла А. Ответ дайте в градусах.

Ответ: 30

3. 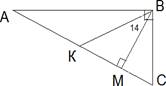                       а) В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14°. Найдите угол МВС. Ответ дайте в градусах.

Ответ: 31

б) В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.

Ответ: 31

в) В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен 20°. Найдите больший угол прямоугольного треугольника. Ответ дайте в градусах.

Ответ: 65

4. 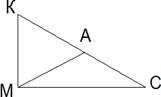                       а) В прямоугольном треугольнике МСК с прямым углом М найдите СА, если МА – медиана и КС

= 13.

Ответ: 6,5

б) В прямоугольном треугольнике МСК с прямым

углом М найдите длину медианы МА, если гипотенуза КС равна 34.

Ответ: 17

в) В прямоугольном треугольнике МСК с прямым углом М найдите длину гипотенузы КС, если медиана МА равна 6.

Ответ: 12

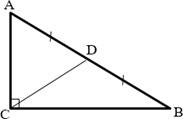
5.                        а) В треугольнике ABC CD – медиана,

∠𝐴𝐶𝐵 = 90⁰ , ∠𝐵 = 15⁰ . Найдите угол BCD. Ответ дайте в градусах.

Ответ: 15

б) В треугольнике ABC CD – медиана, ∠𝐴𝐶𝐵 = 90⁰ , ∠𝐴 = 20⁰ . Найдите угол BCD. Ответ дайте в градусах.

Ответ: 70

в) В треугольнике ABC CD – медиана, ∠𝐴𝐶𝐵 = 90⁰, ∠𝐵 = 35⁰. Найдите угол ACD. Ответ дайте в градусах.

Ответ: 55

6.                        а) В треугольнике ABC проведена биссектриса CE. Найдите величину угла BCE, если ∠BAC = 46° и ∠ABC = 78°. Ответ дайте в градусах.

Ответ: 28

б) В треугольнике ABC проведена биссектриса CE. Найдите величину угла

BAC, если ∠ACE = 16° и ∠ABC = 96°. Ответ дайте в градусах.

Ответ: 52

в) В треугольнике ABC проведена биссектриса CE. Найдите величину угла

ACE, если ∠BAC = 101° и ∠ABC = 33°. Ответ дайте в градусах.

Ответ: 23

7.                          а) В треугольнике ABC угол A равен 25⁰, угол B равен 89⁰. AD, BE и CF – биссектрисы, пересекающиеся в точке O. Найдите угол AOВ. Ответ дайте в градусах.

Ответ: 123

б) В треугольнике ABC угол A равен 48⁰, угол B равен 100⁰. AD, BE и CF – биссектрисы, пересекающиеся в точке O. Найдите угол AOВ. Ответ дайте в градусах.

Ответ: 106

в) В треугольнике ABC угол A равен 30⁰, угол B равен 70⁰. AD, BE и CF – биссектрисы, пересекающиеся в точке O. Найдите угол AOВ. Ответ дайте в градусах.

Ответ: 130

Задачи с развернутым ответом

1. 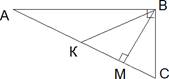                     Острые углы прямоугольного треугольника равны 74° и 16°. Найдите угол между высотой ВМ и медианой ВК, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Ответ: 58.

2.                      В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла равен 18⁰. Найдите больший угол данного треугольника. Ответ дайте в градусах.

Ответ: 63.

3.                      В треугольнике ABC CH – высота, AD – биссектриса, O – точка пересечения прямых CH и AD, угол BAD равен 74⁰. Найдите угол AOC. Ответ дайте в градусах.

Ответ: 16.