Поделиться
1.5_9__Қосымша-4 дәлелдеу.docx
Қосымша 4
Оқушылар қосу формулаларын дәлелдейді
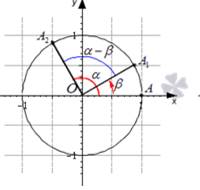
Дәлелдеуі:
1. А1 және A2 нүктелерінің координаталарын жазыңыз______________________________________________________________________
2. OA1 және OA2 радиус векторларының координаталарын жазыңыз _____________________________________________________________________________
3.
векторлардың скаляр көбейтіндісін жазыңыз _____________________________________________________________________________
4.Векторлардың скаляр көбейтіндісін координаталармен жазыңыз
=___________________________________________________________________
5.Үшінші және төртінші қадамдардын нәтежесін теңестіріңіз___________________________________________________________________
6. 
-формуласын қалай дәлелдейміз?
____________________________________________________________________________
7. sin(
)=
(3) дәлелдеу
үшін келтіру формуласын қолданайық
sin(
)=cos(
)= __________________________________________________________________________________
8.
қолдансақ онда
sin(
) =_________________________________________________________________________
9.Келесі формулаларды өздігімен дәлелдеңіp
a)tg(
)=
b) tg(
)=
c)ctg(
)=
d) ctg(
)=
Оқушылар қосу формулаларын дәлелдейді
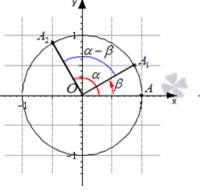
Дәлелдеуі:
1. А1 және A2 нүктелерінің
координаталарын жазыңыз(А1(cos
;sin
) A2(cos
;sin
))
2. OA1 және OA2 радиус векторларының
координаталарын жазыңыз (OA1(cos
;sin
) OA2 (cos
;sin
) )
3.
векторлардың скаляр көбейтіндісін жазыңыз
(
=
=1
=
)
4.Векторлардың скаляр көбейтіндісін координаталармен жазыңыз
((
) =
)
5.Үшінші және төртінші қадамдардын нәтежесін теңестіріңіз
=
(1)
6. 
-формуласын қалай дәлелдейміз?
онда cos(
)=
(2)
7. sin(
)=
(3) дәлелдеу
үшін келтіру формуласын қолданайық
sin(
)=cos(
)= cos(
) =
cos(
(
(3)
8.
қолдансақ онда
sin(
)=sin(
) = sin
cos
=
sin
cos
(4)
9.Келесі формулаларды өздігімен дәлелдеңіз
a)tg(
)=
b) tg(
)=
c)ctg(
)=
d) ctg(
)=
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
