17“Study of the flight distance-angle of departure relationship”

Safety procedures

1. Follow directions. Come to lab prepared to perform the experiment. Follow all written and verbal instructions. When in doubt, ask.
2. Absolutely no horseplay. Be alert and attentive at all times. Actlikeanadult.
3. Report all accidents, injuries or breakage to the instructor immediately. Also, reportanyequipmentthatyoususpectismalfunctioning.
4. Dress appropriately. Avoid wearing overly-bulky or loose-fitting clothing, or dangling jewelry that may become entangled in your experimental apparatus. Pin or tie back long hair and roll up loose sleeves.
5. Usegoggles:
1. whenheatinganything.
2. when using any type of projectile.
3. when instructed to do so.
6. Use equipment with care for the purpose for which it is intended.
7. Do not perform unauthorized experiments. Get the instructor's permission before you try something original.
8. Be careful when working with apparatus that may be hot. If you must pick it up, use tongs, a wet paper towel, or other appropriate holder.
9. If a thermometer breaks, inform the instructor immediately. Do not touch either the broken glass or the mercury with your bare skin.
10. Ask the instructor to check all electrical circuits before you turn on the power.
11. When working with electrical circuits, be sure that the current is turned off before making adjustments in the circuit.
12. Do not connect the terminals of a battery or power supply to each other with a wire. Such a wirewillbecomedangerouslyhot.
13. Return all equipment, clean and in good condition, to the designated location at the end of the lab period.
14. Leave your lab area cleaner than you found it.

Theoretical material

When firing a projectile over a horizontal surface at different angles to the horizontal, the range of the projectile is expressed by the formula

From this formula, it follows that when the launch angle of the projectile changes from 90 to 0°, the range of its flight first increases from zero to some maximum value, and then again decreases to zero. The range of the projectile is maximal when sin2a has the greatest value (=1). This dependence in this work should be verifiedexperimentally by means of the ballistic gun shown in Fig. 13.1.

The gun is a spiral spring (1) with a rod along the axis, mounted on a bracket (2) with a protractor (3). On the rod is placed a special ball (4), which has a hole that fits around the rod. Afterplacing the ball, the spring is compressed and hooked in place so that the ball is behind the trigger at the base of the spring. If you push the protruding part (5) of the trigger, the ball is released and under the force of the spring moves along the rod in a given direction.

The magnitude of the initial velocity(launch velocity) the ball (v₀) is assumed to be the same for all experiments

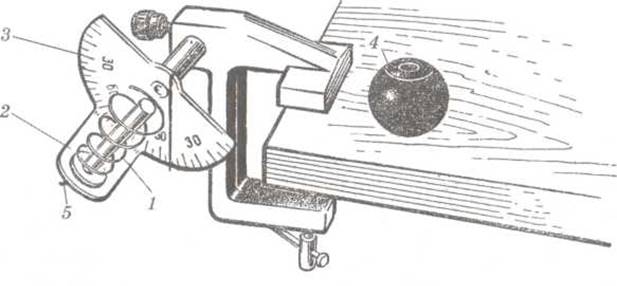
On the table where the ball lands a piece of carbon paper should be fixed in place with two pieces of scotch tape.On top of this should be taped in place a piece of copy paper. When the ball hits the paperit will leavea mark.

Additional differentiated tasks and problems

Problem 1

An object is launched at a velocity of 20 m/s in a direction making an angle of 25° upward with the horizontal.

a) What is the maximum height reached by the object?

b) What is the total flight time (between launch and touching the ground) of the object?

c) What is the horizontal range (maximum x above ground) of the object?

d) What is the magnitude of the velocity of the object just before it hits the ground?

Problem 2

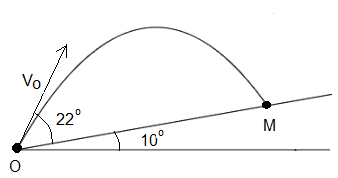
A projectile is launched from point O at an angle of 22° with an initial velocity of 15 m/s up an incline plane that makes an angle of 10° with the horizontal. The projectile hits the incline plane at point M.
a) Find the time it takes for the projectile to hit the incline plane.
b)Find the distance OM.

Problem 3

A projectile is to be launched at an angle of 30° so that it falls beyond the pond of length 20 meters as shown in the figure.
a) What is the range of values of the initial velocity so that the projectile falls between points M and N?

Problem 4

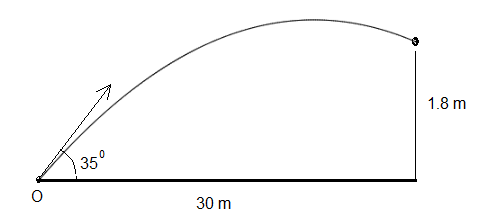
A ball is kicked at an angle of 35° with the ground.
a) What should be the initial velocity of the ball so that it hits a target that is 30 meters away at a height of 1.8 meters?
b) What is the time for the ball to reach the target?

Problem 5

A ball kicked from ground level at an initial velocity of 60 m/s and an angle θ with ground reaches a horizontal distance of 200 meters.

a) What is the size of angle θ?

b) What is time of flight of the ball?