1Electromagnetic induction. Magnetic flux and flux linkage

Discussion and demonstration: Induction effects
The first two demonstrations involve moving a wire in a magnetic field and then a permanent magnet into and out of a small coil. In both it is important to emphasise that:

Ø  ‘electricity’ is only produced while something is moving

Ø  the faster the movement, the more ‘electricity’ we get

Cutting magnetic field lines

Start by thinking about a simple bar magnet. It has a magnetic field in the space around it. We represent this field by magnetic field lines. Now think about what happens when a wire is moved into the magnetic field (Figure). As it moves, it cuts across the magnetic field. Remove the wire from the field, and again it must cut across the field lines, but in the opposite direction. We think of this cutting of a magnetic field by a conductor as the effect that gives rise to an induced current in the conductor. It doesn’t matter whether the conductor is moved through the field or the magnet is moved past the conductor, the result is the same – there will be an induced current.

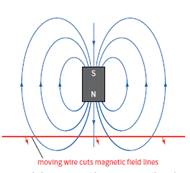
For a coil of N turns, the effect is N times greater than for a single turn of wire.

When the coil is outside the field, there are no magnetic field lines linking the coil.

When it is inside the field, field lines link the coil. Moving the coil into or out of the field changes this linkage, and this induces an e.m.f. across the ends of  the coil.

Magnetic flux and magnetic flux linkage

Magnetic flux density B is defined by the equation

B = F/IL

Now we can go on to define magnetic flux as a quantity.

We picture magnetic flux density B as the number of magnetic field lines passing through a region per unit area.

Similarly, we can picture magnetic flux as the total number of magnetic field lines passing through an area A. For a magnetic field normal to A, the magnetic flux Φ must therefore be equal to the product of magnetic flux density and the area A.

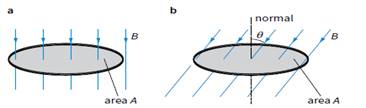
a The magnetic flux is equal to BA when the field

    is normal to the area.

b The magnetic flux becomes Bacosθ  when the field is at an angle θ to the normal of the area.

The magnetic flux Φ through area A is defined as:

Φ = BA

where B is the component of the magnetic flux density perpendicular to the area.

How can we calculate the magnetic fl ux when B is not perpendicular to A?

When the field is parallel to the plane of the area, the magnetic flux through A is zero. To find the magnetic flux in general, we need to find the component of the magnetic flux density perpendicular to the area.

Magnetic flux = (B cos θ) × A

or simply:

Magnetic flux = BA cos θ

(Note that, when θ = 90°, flux = 0 and when θ = 0°,

flux = BA.)

For a coil with N turns, the magnetic flux linkage is defined as the product of the magnetic flux and the number of turns; that is:

Magnetic flux linkage = NΦ

or

Magnetic flux linkage = BAN cos θ

The unit for magnetic flux or flux linkage is the Weber (Wb).

One weber (1 Wb) is the flux that passes through an area of 1 m² when the magnetic flux density is 1 T.

1 Wb = 1 T m².

An e.m.f. is induced in a circuit whenever there is a change in the magnetic flux linking the circuit. Since magnetic flux is equal to BA cos θ, there are three ways an e.m.f. can be induced:

■■ changing the magnetic flux density B

■■ changing the area A of the circuit

■■ changing the angle θ.