1.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: 6.2.2.16 знать определение линейного уравнения с двумя переменными и его свойства;

Критерии оценивания:

- знают определение линейного уравнения с двумя переменными;

- умеют применять свойства линейного уравнения с двумя переменными;

Организационный момент. Предложите учащимся проблемную ситуацию.

Задача: Из городов А и Б, расстояние между которыми 400 км, навстречу друг другу выехали два автомобиля, каждый со своей постоянной скоростью. Первый автомобиль вышел на час раньше второго. А через 2 часа после выезда второго автомобиля они встретились. Чему равны скорости автомобилей.

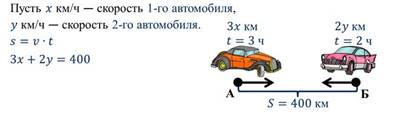
Полученное равенство содержит две переменные.
А поэтому такие неравенства называют уравнением с двумя переменными.

Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное числовое равенство.

          Объедините учащихся в группы по 3–4 человека. Предложите каждой группе комплект карточек, на которых записаны различные уравнения.

 Попросите учащихся отсортировать карточки по виду уравнения. Каждая группа учащихся демонстрирует свою сортировку, объясняя свой выбор.

Из предложенных уравнении выберите линейное уравнение с двумя переменными:

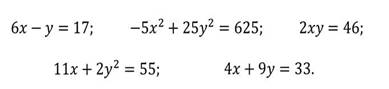
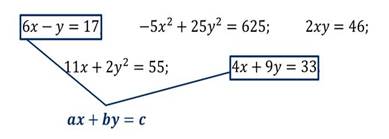
Напомните учащимся определение равносильных уравнений и свойства линейных уравнений с одной переменной.

Свойства линейного уравнения с двумя переменными:

Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;

. Если обе части уравнения умножить или разделить на одно и тоже отличное от нуля число, то получится уравнение, равносильное данному;

          Попросите учащихся проверить данные свойства для линейных уравнений с двумя переменными. Подтвердить свои выводы примерами.

Рассмотрим уравнение:  (1)

Воспользовавшись свойствами уравнений, выразим из этого уравнения одну переменную через другую, например. Для этого перенесем слагаемое  в правую часть уравнения, изменив его знак:

Разделим обе части на 2:

        (2)

Уравнение (2) равносильно уравнению (1). Пользуясь формулой   можно найти сколько угодно решений уравнения(1). Для этого достаточно взять произвольное  и вычислить соответствующее ему значение

Например:

если

если

Пары чисел (2;1), (0,4;5) – решения уравнения (1).

Уравнение (1) имеет бесконечно много решений.

Фронтальная работа. Работа в парах. Взаимное обучение.

           Создайте пары с разным уровнем обучаемости. Предложите учащимся задания для взаимного обучения: учащиеся будут объяснять решение задачи своему напарнику при возникновении вопроса по той или иной задаче, т.е. учащиеся выполняют задания индивидуально, но имеют возможность обсудить непонятные вопросы с напарником.

 Учащиеся в парах обмениваются решениями и проводят самооценивание и взаимооценивание.

1.Пары значений переменных указаны в таблице:

Какие из них являются решениями уравнения:

Ответ:

2. Мадина купила карандаши по 7 тг и ручки по 35 тг. За все она заплатила 210 тг. Сколько карандашей и сколько ручек могла купить Мадина?

Ответ: (25;1); (20;2); (15;3); (10;4); (5;5)

3. Найдите значение , если уравнение   имеет решения:

Ответ: 3,5;0;7

4.Расстояние между городами 54 км. Сначала велосипедист ехал со скоростью 12 км/ч, затем со скоростью 10 км/ч. Сколько часов ехал велосипедист со скоростью 12 км/ч? Сколько часов он ехал со скоростью 10 км/ч?

Ответ: 2ч; 3 ч

Дескриптор:

- проверяет, что пара чисел является решением линейного уравнения с двумя переменными

- выполняет действия с числами;

-выбирает пары чисел, являющиеся решением уравнения;

Проведите с учащимися физкультминутку.

       Предложите учащимся для отработки навыков решения линейного уравнения с двумя переменными прием Карусель.

Каждая группа получает карточку с заданиями, которые должна выполнить. Каждый ученик выбирает одно из уравнении и выполняет его решение. Решение задания учащийся может обсудить с учащимися, выполняющими решение этого уравнения из других групп. По завершении работы, каждый ученик объясняет решение своего уравнения внутри группы. Решение всех уравнении группы выполняют на постере.

Для организации взаимопроверки постеры всех групп распределите по группам, выполнявших решение других заданий.

Задания:

1.Является ли пара чисел  решением уравнения

Ответ:

2.Какие из пар чисел являются решениями уравнения

?

Ответ: (3;1); (0;10); (2;4)

3.Из линейного уравнения 12 выразите:

а)

b)

Ответ:    b)  

4.Из уравнения  выразите:

а) u

b)

Ответ:

5.Среди решений уравнения  найдите такую пару, которая составлена из одинаковых чисел.

Ответ: (6;6)

Дескриптор:

- проверяет, что пара чисел является решением линейного уравнения с двумя переменными

- выполняет действия с числами;

-выбирает пары чисел, являющиеся решением уравнения;

Рефлексия.

Подведение итогов урока. Рефлексия.

Учащиеся выполняют саморефлексию, отвечая на вопросы:

- что узнал, чему научился?

- что осталось непонятным?

-над чем необходимо работать?

Домашнее задание: № 1428 стр.344

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова. Алматы. Атамура. 2011 год.