25 дарс

“Tasdiqlayman”

O`zbekiston Respublikasi Milliy gvardiyasi 

Toshkent "Temurbeklar maktabi" harbiy akademik litseyi

o’quv ishlari bo’yicha direktor o’rinbosari__________ A.Xaydarov

“____” _________ 2021 yil

1.1.O’quv mashg’ulotining ta’lim texnologiyasi modeli

1.2. “O‘tkir burchakli uchburchaklar uchun tengsizliklar. Uchburchakda turli tengsizliklar. ”mavzusi bo'yicha o'quv mashg'ulotining texnologik xaritasi 

Kirish

Sаlоmlаshish: Sаlоmlаshish ikki mаqsаdgа yo‘nаltirilgаn. Birinchisi chindаn hаm sаlоmlаshishni nаzаrdа tutаdi: hаmmаgа хаyrli  (mаsаlаn : tоng, kun, оqshоm) tilаsh. Ikkinchisi –  siz аuditоriya оldidа turgаnligingizgа diqqаtni jаlb etish. Shuning uchun o‘qituvchining sаlоmlаshuvi mаksimаl dаrаjаdа ijоbiy, sаmimiy, do‘stоnа, hаmkоrlikkа chоrlоvchi bo‘lishi kеrаk.

Dаvоmаtni tеkshirish:Bu bоsqichdа o‘qituvchi dаvоmаtni nаzоrаt qilаdi, mахsus jurnаlgа o‘quvchilаrning dаrsgа kеlgаn yoki yo‘qligini qаyd etаdi, imkоn qаdаr dаrsgа qаtnаshmаgаnlik sаbabini аniqlаydi.Darsni nazorat bilan boshlaydi .

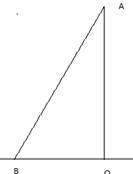
.To’g’ri burchakli uchburchakda gipotenuza katetlarning har biridan katta.

Teskari teorema: har qanday uchburchakda:

1)    Teng burchaklar qarshisida teng tomonlar yotadi.

2)    Katta burchak qarshisida katta tomon yotadi.

1-natija: uchburchakning bir tomoni qolgan ikki tomoni ayirmasidan kichik.

2-natija: Ikki nuqtani tutashtiruvchi to’gri chiziq kesmasi, bu nuqtalarni tutashtiruvchi har qanday siniq chiziqdan kichik.

3-natija: Agar to’g’ri burchakli uchburchakda o’tkir burchaklarni  biri 30 ga teng bo’lsa, u holda bu burchak qarshisida yotgan katet, gipotenuzaning yarmiga teng.

Ta’rif: Agar qo’shni burchaklar o’zaro teng bo’lsa, qo’shni burchaklarning umumiy tomoni ustma-ust tushmagan tomonlardan tuzilgan to’g’ri chiziqqa perpendikulyar(tik) deyiladi. Qo’shni burchaklar teng bo’lmasa, umumiy tomon umumiy bo’lmagan tomonlardan tuzilgan to’g’ri chiziqqa og’ma deyiladi. Burchakning uchi bo’lgan nuqta mos ravishda perpendikulyarning yoki og’maning asosi deyiladi.

to’g’ri chiziqdan tashqarida yotgan A nuqtadan perpendikulyar va og’ma tushirilgan bo’lsin.  AO – perpendikulyar, O – perpendikularning asosi, AB – og’ma.B og’maning asosi.

          Kesmaning to’g’ri chiziqqa proyeksiya deb, shu kesmaning oxirlaridan to’g’ri chiziqqa tushirilgan perpendikulyarning asoslari orasidagi kesmaga aytiladi. Ravshanki, proeksiyalanayotgan kesma to’g’ri chiziqqa perpendikulyar bo’lsa, uning shu to’g’ri chiziqqa proyeksiyasi nuqta bo’ladi.

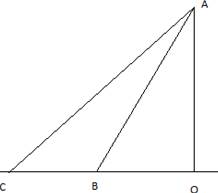
          Teorema. Berilgan nuqtadan berilgan to’g’ri chiziqqa o’tkazilgan perpendikulyar berilgan nuqtadan shu to’g’ri chiziqqa o’tkazilgan har qanday og’madan kichik. To’g’ri chiziqqa og’malar o’tkazilgan bo’lsa, proyeksiyasi katta bo’lgan og’ma kattadir.

Isboti. AO perpendikulyar, AB va AC og’malar bo’lsin. AB va AC og’malarning proyeksilari OB<OC tengsizlikni qanoatlantiradi. AO<AB,  AC>AB tengsizliklarni isbot qilishimiz kerak.          ΔAOB da ∠O – to’g’ri burchak, ∠B – o’tkir burchak, ya’ni ∠B <∠O. Bundan  uchburchakning katta burchagi  qarshisida katta tomon yotishiga ko’ra AO<AB.

          Endi AB<AC ni isbot qilaylik. ΔABC da ∠ABC o’tmas burchak, chunki u ∠ABO o’tkir burchakka qo’shni burchak.ΔABC  da∠ACB o’tkir burchak, chunki u to’g’ri burchakli ΔAOC ning to’g’ri burchagidan boshqa ichki burchagi. Bulardan ∠ABC>∠ACB.Bundan AC>AB kelib chiqadi.

          Agar og’malar O nuqtadan turli tomonlarda o’tkazilgan bo’lsa, ulardan birining proyeksiyasiga teng proyeksiyali og’mani O nuqtadan bir tomonda hosil qilishimiz va shu tomondagi og’ma bilan taqqoslashimiz mumkin.

          Quyidagi teoremalarni isbotlash o’quvchilarga tavsiya qilinadi.

          Teorama. To’g’ri chiziqqa bir nuqtadan tushirilgan ikki og’maning  qaysi biri katta bo’lsa, shu og’maning proeksiyasi kattadir.

          Teorema.  Proeksiyalari teng bo’lgan og’malar teng va, aksincha, og’malar teng bo’lsa, ularninig proeksilari ham tengdir.

to’g’ri chiziqdan tashqarida yotgan A nuqtadan perpendikulyar va og’ma tushirilgan bo’lsin.

AO- perpendikulyar, O- perpendikulyarning asosi,  AB-og’ma, B- og’ma asosi, AB og’maning proeksiyasi OB kesmadan iborat.

Kesmaning to’g’ri chiziqdagi proeksiyasi deb, shu kesmaning oxiridan to’g’ri  chiziqqa tushirilgan perpendikulyarning asoslari orasidagi kesmaga aytiladi.

Chizmada A₁ B₁kesma , AB kesmaning to’g’ri chiziqdagi proeksiyasidir. Agar proeksiyalanayotgan kesma to’g’ri chiziqqa perpendikulyar bo’lsa, uning shu to’g’ri  chiziqqa proyeksiyasi nuqta bo’ladi.

Teorema: biror nuqtadan to’g’ri chiziqqa o’tkazilgan perpendikulyar o’sha nuqtadan shu to’g’ri chiziqqa  o’tkazilgan har qanday og’madan qisqadir.

       To`g`ri burchakli uchburchak uchun o`rinli bo`ladigan tengsizliklar :                                                                                     

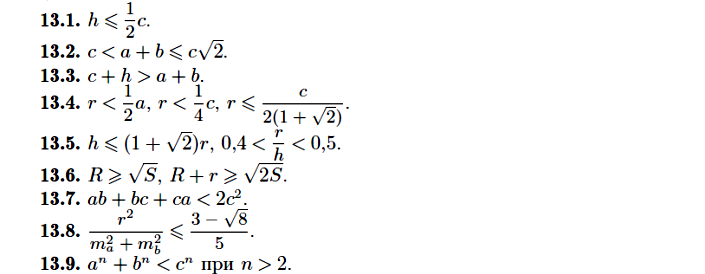
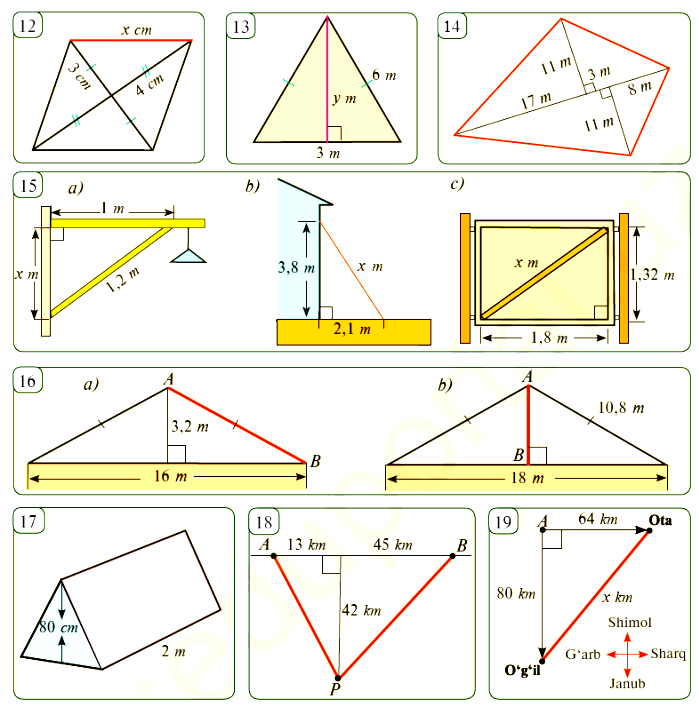
Nаzоrаt: mаzkur bоsqichning mаqsаdi – o‘quvchilаrdа hоsil bo‘lgаn bilimlаrni tеkshirish. O‘quvchilаrgа o‘tilgаn mаvzu bo‘yichа hоsil bo‘lgаn bilimlаrni tеkshirib ko‘rish tаklif etilаdi, bundа mахsus tаrqаtmа mаtеriаllаrdаn fоydaliniladi.