
Задание 1 группы:
1.
Случайным образом выбирают одно из решений неравенства ![]() ,
какова вероятность, того что это решение окажется решением неравенства
,
какова вероятность, того что это решение окажется решением неравенства ![]() .
.
Решение. Что такое модуль с геометрической точки зрения? Правильно
он показывает расстояние между точками стоящими под знаком модуля. ![]() – означает что расстояние между х
и 5 расстояние не больше 2. Изобразим решение неравенства:
– означает что расстояние между х
и 5 расстояние не больше 2. Изобразим решение неравенства:
![]()
Длина получившегося отрезка равна 4.
По аналогии![]() – означает что расстояние между х
и 2 расстояние не больше 13.
– означает что расстояние между х
и 2 расстояние не больше 13.
![]()
Длина получившегося
отрезка 24. Ответ: ![]()
Задание 2 группы:
2. Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждут друг друга в течение 5 минут?
Решение: Используем геометрическое определение вероятности события A = (Встреча с другом состоится).
Обозначим за х и у время прихода, ![]() (минут).
В прямоугольной системе координат этому условию удовлетворяют точки, лежащие
внутри квадрата ОАВС.
Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то
есть
(минут).
В прямоугольной системе координат этому условию удовлетворяют точки, лежащие
внутри квадрата ОАВС.
Друзья встретятся, если между моментами их прихода пройдет не более 5 минут, то
есть
![]()
Этим неравенствам удовлетворяют точки, лежащие в области G, окрашенного в голубой цвет.
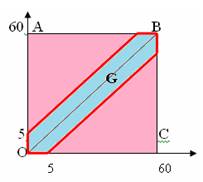
Тогда вероятность встречи равна отношению площадей области G и квадрата, то есть
![]()
Ответ: 0,16
Задание 3 группы:
3. Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что:
а) Арман встретится с Айнурой во время обеда;
б) данная встреча не состоится.
Решение: Используем геометрическое
определение вероятности события A = Встреча
Армана и Айнуры состоится, ![]() – их
встреча не состоится.
– их
встреча не состоится.
Обозначим за х и у время прихода, ![]() (минут).
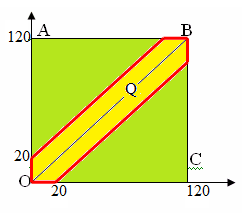
В прямоугольной системе координат этому условию удовлетворяют точки, лежащие
внутри квадрата ОАВС.
Студенты встретятся, если между моментами их прихода пройдет не более 20 минут,
то есть
(минут).
В прямоугольной системе координат этому условию удовлетворяют точки, лежащие
внутри квадрата ОАВС.
Студенты встретятся, если между моментами их прихода пройдет не более 20 минут,
то есть
![]()
Этим неравенствам удовлетворяют точки, лежащие в области Q, окрашенного в желтый цвет.
Тогда вероятность встречи равна отношению площадей области Q и квадрата, то есть
![]()
![]()
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.