3. Методические рекомендации к проведению урока. Вариант 1.

Методические рекомендации к проведению урока

Тема: Расположение фигур в пространстве. Изображение пространственных фигур, «невидимые» линии.

Цель обучения: 6.3.2.4 распознавать фигуру по её изображению и изображать плоские и пространственные фигуры.

Актуализация знаний учащихся.

«Конструктор»

Развертка какой фигуры изображена на рисунке? Перенеси ее на лист бумаги, увеличив размеры в 4 раза, затем вырежи и сверни в многогранник.

Ответ: пирамида.

Ознакомление учащихся темой урока и постановка целей обучения.

Объяснение построения на изометрической бумаге.

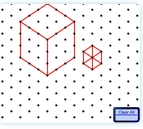
Построение на изометрической бумаге.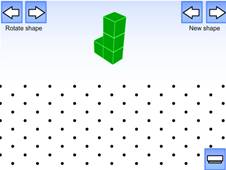

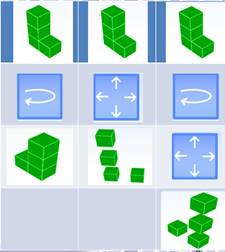
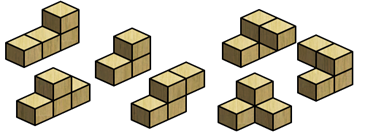
№1. Из скольких кубиков состоит фигура?

№2. Постройте эти фигуры с помощью кубиков (элементы конструктора) и нарисуйте на изометрической бумаге.

Установление каллобартивной среды обучения

Практическая работа

Задания

№511.

Вырежи из картона прямоугольник, прямоугольный треугольник, круг и закрепи их на стержне. Вращая стержень между ладонями, и наблюдай, как образуется цилиндар, конус, шар.

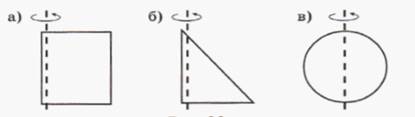
Работа с классом

Задание

№512.

Нарисуйте в масштабе 1:4 тело вращения и три его проекции, если оно получается в результате вращения:

a) прямоугольника со сторонами 10 см и 4 см вокруг большей стороны;

b)  прямоугольного треугольника с катетами 6 см и 8 см вокруг меньшего катета;

c) круга с радиусом 6 см вокруг диаметра.

№517.

Нарисуйте в масштабе 2:1 геометрические тела, которые  получаются при вращении вокруг прямой l данных фигур на следующем рисунке. Опишите их.

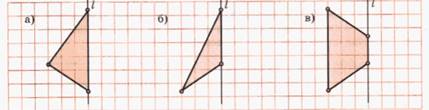
Дескриптор. Учащийся:

-         изображает тело вращения;

-         описывает тело вращения.

Оценивание осуществляется с помощью дескриптора.

Работа в парах

Задание

№490.

Леонард Эйлер открыл удивительную формулу зависимости между числом вершин (В), числом ребер (Р) и числом граней (Г) выпуклого многогранника. Восстанови этк формулу по записи:

№491.

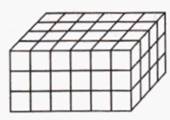a) На рисунке прямоугольный параллелепипед сложили из одинаковых кубиков. Сколько кубиков для этого понадобилось?

b) Запишите формулы объема и площади полной поверхности прямоугольного параллелепипеда с измерениями a, b, c.

c) Запишите формулы объема и площади полной поверхности куба с ребром a.

№492.

a) Хваит ли проволоки длиной 1 метр, чтобы сделать каркасную модель прямоугольного параллелепипеда с измерениями 7 см, 9 см и 14 см?

b) Прямоугольный лист бумаги имеет размеры 8 см и 12 см. Достаточно ли этого листа, чтобы оклеить всю поверхность прямоугольного параллелепипеда с измерениями 3 см, 4 см и 5 см?

Дескриптор. Учащийся:

-         знают измерения прямоугольного параллелепипеда;

-         вычисляют площадь его полной поверхности.

Взаимооценивание осуществляется с помощью дескриптора.

Индивидуальная работа

№524.

При строительстве дома по известным размерам стен можно вычислить, сколько кирпичей потребуется для укладки его стен. Для этого используется формула:

где N – количество кирпичей, l м – длина стены, h м – высота стены.

а) найдите N, если .

b) найдите , если .

c) найдите, если .

Ответ округлите  с точностью до десятых. В каждом случае придумайте соответствующую задачу.

Ответ: а) 1708; b) 16; c) 20,5.

Дескриптор. Учащийся:

-         знают измерения прямоугольного параллелепипеда;

-         вычисляют площадь его полной поверхности.

Самооценивание осуществляется с помощью дескриптора.

Итоги урока:

Что такое тело вращение?

Как изображается проекция тел вращения?

Рефлексия

Домашнее задание:

№500.

Склейте из бумаги модель тетраэдра, гранями которого вяляются равносторонние треугольники со стороной 10 см.

№501.

Склейте из бумаги прямоугольный параллелепипед с измерениями 9 см, 5 см и 3 см. Начертите три его проекции в масштабе 1:2.

 Дескриптор. Учащийся:

-         знает измерения прямоугольного параллелепипеда;

-         вычисляют площадь его полной поверхности;

изображает три его проекции.

Список полезных ссылок и литературы

1.     http://www.teacherled.com/2007/11/28/isometric-grid/

2.     http://www.teacherled.com/resources/isodotty/isodottyload.html

3.     http://www.teacherled.com/2008/03/18/isometric-shape-draw/

4.     http://www.teacherled.com/resources/isodraw/isoshapeload.html

5.     https://www.math-salamanders.com/geometry-nets.html

6.     Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Часть 3. – Изд. 2-е, перераб./ Г.В. Дорофеев, Л.Г. Петерсон. – М.: Издательство «Юнита», 2010. – 176 с.: ил.

7.     Скачано с www.znanio.ru