Добавить материал

и получить 10 документов
и свидетельство автора

Изображение пользователя Черная Марина Николаевна Черная Марина Николаевна

383- ЕГЭ-2016. Информатика. Тем. тест. задания_Крылов_2016 -272с.pdf

  • pdf
  • 29.04.2020
Публикация на сайте для учителей

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал
Иконка файла материала 383- ЕГЭ-2016. Информатика. Тем. тест. задания_Крылов_2016 -272с.pdf

СОЗДАНО РАЗРАБОТЧИКАМИ ФИПИ

ИНФОРМАТИКА

iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii

! ТЕМАТИЧЕСКИЕ

ТЕСТОВЫЕ ЗАДАНИЯ

*0tt

ЕГЭ

ИНФОРМАТИКА

Теория

Тематические задания

Задания формата ЕГЭ

Диагностический вариант экзаменационной работы Контрольные варианты

Ответы

Издательство

«ЭКЗАМЕН» МОСКВА, 2016

удк 372.8:002

ББК 74.263.2

k85

Крылов С. С.

           k85           ЕГЭ 2016. Информатика. Тематические тестовые задания / С. С. Крылов; Д. М. Ушаков. — М.

                   Издательство <<Экзамен», 2016.   270, [2] с. (Серия «ЕГЭ. ФИПИ. Тематические тестовые задания»)

ISBN 978-5-377-09817-1

Тематические тестовые задания по информатике, созданные специалистами Федерального института педагогических измерений, ориентированы на подготовку учащихся средней школы к успешной сдаче ЕГЭ.

Книга содержит множество тематических заданий для отработки каждого элемента содержания ЕГЭ по информатике, а также диагностический и контрольные варианты экзаменационной работы.

Уникальная методика подготовки, разработанная специалистами ФИПИ, поможет учащимся научиться правильно оформлять работу, выявлять критерии оценивания, акцентировать внимание на формулировках ряда заданий и избегать ошибок, связанных с невнимательностью и рассеянностью на экзамене.

Использовать предлагаемые тестовые задания можно как в классе, так и дома.

Книга рассчитана на один учебный год, однако при необходимости позволит в кратчайшие сроки выявить пробелы в знаниях ученика и отработать задания, в которых допускается больше всего ошибок, непосредственно за несколько дней до экзамена.

Издание предназначено для учителей информатики, родителей и репетиторов, а также учащихся средней школы.

Приказом N2 729 Министерства образования и науки Российской Федерации учебные пособия издательства <<Экзамен» допущены к использованию в общеобразовательных организациях.

удк 372.8:002 ББК 74.263.2

Формат 60х90/8. Гарнитура «Школьная».

Бумага газетная. Уч.•изд. л. 15,23. Усл. печ. л. 34. Тираж 7000 экз. Заказ 2643/15.

ISBN 978-5-377-09817-1                                                                           О Крылов С. С., Ушаков Д. М., 2016

О Издательство «ЭКЗАМЕН», 2016

 СОДЕРЖАНИЕ

Введение

Диагностический вариант экзаменационной работы

Ответы к диагностическому варианту экзаменационной работы . 19 1. Количество информации. Скорость передачи информации. 24

2. Системы счисления . 36

З. Кодирование информации. 58

4.       Основы логики . 72

5.       Алгоритмизация и программирование. 93

6.       Информационные модели. 163

7.       Определение выигрышной стратегии игры (Анализ и построение дереваигры) . . . 171

8.       Файловая система компьютера

9.       Электронные таблицы

10.  Базы данных

11.  Сетевые технологии

Ответы

Вариант 1

Вариант 2. 246

Ответы к контрольным вариантам экзаменационной работы. 259

Вариант 1. 259

Вариант 2. 266

ВВЕДЕНИЕ

При создании этого учебного пособия использован более чем пятилетний опыт проведения Единого государственного экзамена по информатике. В предлагаемой рабочей тетради приведены задания по всем темам экзамена, каждая глава соответствует определенной теме. Порядок расположения заданий внутри каждой главы соответствует логике изложения материала в учебниках, поэтому рабочую тетрадь можно . использовать не только для обобщающего повторения перед экзаменом, но и в качестве учебного пособия в течение всего учебного года.

Поскольку данное издание представляет собой не только сборник типовых заданий в формате ЕГЭ для контроля и самоконтроля, но и учебное пособие, многие задания сформулированы как обычные задачи, в том виде, который наиболее способствует пониманию учебного материала.

В рабочей тетради не рассматриваются вопросы обучения программированию на какомлибо языке, поскольку в разных школах изучаются различные языки программирования, а рассмотрение нескольких языков не предусматривается форматом данной книги. В теме «Программирование» в качестве теоретического материала приведены общие принципы технологии программирования, соблюдение которых необходимо при выполнении заданий ЕГЭ по информатике.

Большинство заданий рабочей тетради снабжено ответами. Часть заданий намеренно оставлена авторами без ответов, для того чтобы их можно было использовать при проведении проверочных работ.

Авторы уверены, что использование данной рабочей тетради и добросовестное выполнение тренировочных заданий обязательно улучшат ваши результаты на экзамене.

Желаем успеха!

ДИАГНОСТИЧЕСКИЙ ВАРИАНТ ЭКЗАМЕНАЦИОННОЙ РАБОТЫ

Инструкция по выполнению работы

Экзаменационная работа состоит из двух частей, включающих в себя 27 заданий. Часть 1 содержит 23 задания с кратким ответом. Часть 2 содержит 4 задания с развёрнутым ответом.

На выполнение экзаменационной работы по информатике и ИКТ отводится З часа 55 минут (235 минут).

Ответы к заданиям 1—23 записываются в виде числа, последовательности букв или цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов N2 1.

            Ответ: 23                                                  

Задания 24—27 требуют развёрнутого решения. В бланке ответов 2 укажите номер задания и запишите его полное решение.

Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, или капиллярной, или перьевой ручек.

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Желаем успеха!

В экзаменационных 'заданиях используются следующие соглашения.

1. Обозначения для логических связок (операций):

а) отрицание (инверсия, логическое НЕ) обозначается (например, „А);

Ь) конъюнкция (логическое умножение, логическое И) обозначается л (например, А л В) либо & (например, А & В);

с) дизъюнкция (логическое сложение, логическое ИЛИ) обозначается v (например, А v В) либо (например А 1 В);

d) следование (импликация) обозначается (например, А В);

е) тожДество обозначается (например, А = В). Выраэкение А В истинно тогда и только тогда, когда значения А и В совпадают (либо они оба истинны, либо они оба ложны);

f) символ 1 используется для обозначения истины (истинного высказывания); символ О для обозначения лжи (ложного высказывания).

2. Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А —5 В и А) v В равносильны, а А v В и А л В неравносильны (значения выражений разные, например, при А 1, В О).

 З. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, —, А л В С л D означает то же, что и А) л В) v (С л D).

Возможна запись А л В л С вместо (А л В) л С. То же относится и к дизъюнкции: возможна запись А v В v С вместо (А v В) v С.

4. Обозначения Мбайт и Кбайт используются в традиционном для информатики смысле — как обозначения единиц измерения, чьё соотношение с единицей «байт» выражается степенью двойки.

                                                                               Часть 1

Ответом к заданиям 1—23 является число, последовательность букв или цифр, которые следует записать в бланк ответов NQ 1 справа от номера соответствующего задания, начиная с первой клеточки, без пробелов и каких-либо дополнительных символов. Каждую букву или цифру пишите в отдельной кпеточке в соответствии с приведенными образцами.

 

 

 

 

 

 

 

 

1

 

 

1

 

1

1

1

1.            По каналу связи передаются сообщения, содержащие только 4 буквы А, В, С, D; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, В, С используются такие кодовые слова: А: 010, В: 1, С: 011. Укажите  кратчайшее кодовое слово для буквы D, при котором код будет . допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Ответ:

2.            Дан фрагмент таблицы истинности логического выражения от пяти аргументов — Х1, Х Х5. Результат логического выражения обозначен буквой Р.

Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение Х1 не совпадает со значением F.

Ответ:

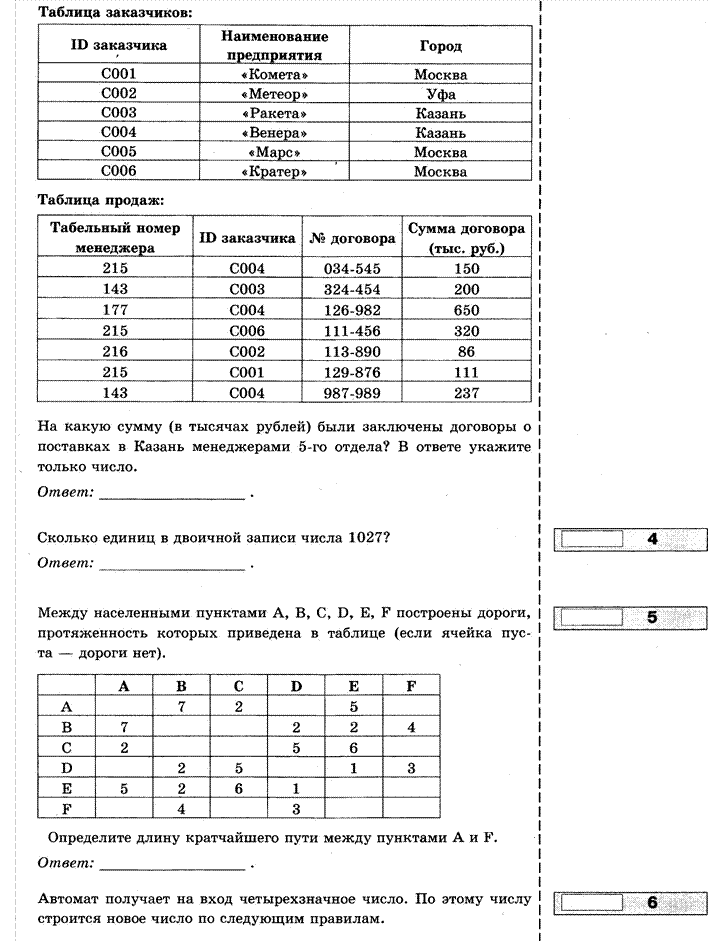
З. База данных о продажах некоторого торгового предприятия состоит из трех связанных таблиц. Ниже даны фрагменты этих таблиц:

Табельный

Фамилия

Должность

Лё отдела

101

Иванов

Менеджер по продажам

6

14

Михайлова

Менеджер по продажам

5

177

Степанов

Менеджер по продажам

з

215

Петренко

Менеджер по продажам

5

216

Зеленчук

Менеджер по продажам

6

з 34

Зверева

Менеджер по продажам

5

                                                  Таблица сотрудников предприятия:

Таблица продаж:

На какую сумму (в тысячах рублей) были заключены договоры о поставках в Казань менеджерами 5-го отдела? В ответе укажите только число.

Ответ:

Ответ:

протяженность которых приведена в таблице (если ячейка пуста — дороги нет).

Определите длину кратчайшего пути между пунктами А и F.

Ответ:

строится новое число по следующим правилам.

1.        Складываются первая и вторая, а также третья и четвертая цифры исходного числа.

2.        Полученные два числа записываются друг за другом в порядке убывания (без разделителей).

Пример. Исходное число: 5348. Суммы: 5 + З = 8; 4 + 8 = 12. Результат: 128.

Укажите наименьшее число, в результате обработки которого автомат выдаст число 1412.

 

 

 

 

 

 

 

 

 

20

 

16

-$А1+С$1

25

44

 

 

 

 

50

Бейсик

 

Паскаль

1024

WHILE А <> 0

2

1

WEND

 

1024; whi1e а <> 0 do begin с div 2;

end;                          

Си

 

Алго итмический язык

1024; while (a ! — 0)

2;

1;

 

1024 нц пока а <> 0 div (с, 2)

кц

 

Python

1024 whi1e а ! =

2

1

 

Ответ:

Дан фрагмент электронной таблицы

Формулу из ячейки В2 скопировали в ячейку СЗ так, что числовое значение ячейки СЗ стало отличаться от числового значения ячейки В2. Каково стало числовое значение ячейки СЗ?

Ответ:

Определите значение переменной с после выполнения следующего фрагмента программы (записанного ниже на разных языках программирования). Ответ запишите в виде целого числа.

Ответ:

Паскаль

 

Си

procedure f (n:integer) ; begin writeln (п) ; if п < 7 then begin f (n+2) ; f (п+З) end end

 

#inc1ude <stdio.h> void f (int п)

printf (”%d” , п) ; if (п<7)

f (n+2) ; f (n+3) ;

Бейсик

 

Алгоритмический язык

FUNCTION

PRINT N

 THEN

F (N+3)

END IF

END FUNCTION

 

алг цел F (цел п) нач вывод п если п < 7 то

F(n+3) все кон

 

hon

Def F (n) • print (п) if п

F(n+2) F(n+3)

 

9.            Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64-битным разрешением. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число, кратное 2.

Ответ:

10.        Все 5-буквенные слова, составленные из букв К, Л, М, записаны в алфавитном порядке.

Вот начало списка:

1.     ккккк 2. ккккл з.     ккккм

4.            ккклк

Запишите слово, которое стоит на 100-м месте от начала списка.

Ответ:

11. Ниже на пяти языках записан рекурсивный алгоритм F.

Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(2)?

Ответ:

вверх

вниз

влево

вправо

сверху свободно

снизу свободно

слева свободно

справа свободно

12                                         12. На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IPадреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г. Восстановите ЛР-адрес.

В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем 1Р-адресу.

                                                             .51                           4.172.15222                 

в

Ответ:

13.       В некоторой стране автомобильный номер состоит из 7 символов. Каждый символ может быть одной из 18 различных букв или десятичной цифрой.

Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и каждый символ кодируется одинаковым и минимально возможным количеством бит.


Определите объем памяти в байтах, отводимый этой программой для записи 50 номеров. В ответе укажите только число.

Ответ:

14.       Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ф, влево е, вправо э.

Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:

Цикл: ПОКА < условие > команда выполняется, пока условие истинно, иначе происходит переход на следующую строку.

Если робот начнет движение в сторону стены (находясь непосредственно рядом с ней), то он сломается и выполняемая им программа прервется.

Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу (и не разрушившись), РОБОТ остановится в той же клетке, с которой он начал движение?

Запрос

Количество найденных страниц (в тысячах)

Па овоз

18

Па оход

36

Паровоз Па оход

40

НАЧАЛО ПОКА снизу свободно вниз

ПОКА справа свободно вправо

ПОКА сверху свободно вверх

ПОКА слева свободно

влево КОНЕЦ

Ответ:

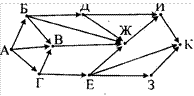
15.       На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Ответ:

16.       Сколько единиц содержится в двоичной записи значения выражения:

                                                                                    2015         2016

Ответ:

17.       В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «'», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу Паровоз & Пароход ?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не I изменялся за время выполнения запросов.

Ответ:

Сколько положительных целых чисел Х удовлетворяют логическому условию

(Х нечетное все цифры Х различны) л Х двузначное?

Ответ:

 

Бейсик

 

 

Паскаль

FOR i

NEXT i

FOR i

1 то 10

9 ТО 1 STEP

-1

for i

for i

A[i+1] :

to 10 do

downto 1 do

=

Си

 

Алгоритмический

for ( i

for

 

нц для i от 1 до 1 0

кц нц для i от 9 до 1 шаг -1 А [1+1] : = А  кц

 

Python

for i in range (1, 11) :

A[i]=i for -i in range (10, 0,

-1 ) :

Паскаль

Си

 

var х, L, М: integer; begin read1n (х) ; о; м   о;

whi1e х do begin м

L + х mod 10; х х div 10; end; write1n (L) ; write (М) ;

void main ( )

int х, L, М; scanf ( 6d &х) ;

о;

whi1e (х > 0)

м х

printf ( ”

ь,

19.        В программе описан одномерный целочисленный массив А с индексами от 1 до 10 и целочисленная переменная i. Ниже представлен фрагмент программы, записанный на разных языках программирования, в котором значения элементов сначала задаются, а затем меняются.

Какое значение примет элемент массива с индексом 4 после выполнения этого фрагмента программы?

Ответ:

20.        Получив на вход число х, алгоритм печатает два числа L и М. Укажите наименьшее из таких чисел х, при вводе которых алгоритм печатает сначала 15, а потом З.

Beicme

 

AaropnmnmecKHi $13b1K

DIM X, L,

INPUT x

L      o

WHILE    >

M      M

x

WEND

PRINT

PRINT

M AS

o

1

X MOD

10

INTEGER

10

 

ajll' Haq

I-len X, L,

BBOA X

       L    o

HI-I F10Ka X > 0

L L + mod (x, 10) x div (x, 10)

KLI

BblBOÄ

KOH

 

 

Python

x   int (input ( ) ) L   o

M o while x>0 do M    M+l

x  x // 10 print (L) ptint (M)

10

IlaCKaJ1b

CH

function f (n: integer) : integer; var i integer; begin s 1;   for to n do s   s f S end; var k, i : integer; begin

read In (k) ;

while f (i) >k do i:=i—l; write (i) ; end.

int f (int n)

int i, s; s  1;

for (i=l i<=n        s  s    2; return s;

void main ( )

int k, i; scanf (" Ood" , & k) 1  12 ; while (f (i) >k)

print f ("%d", i) ;

Omeem:

21.        Hnxce Ha 11flTH fl3b11-cax lipHBeAeHa rrporpararaa. Onpegxe.mnrre,

CKOJ1bKHX pa3JIMt1Hb1X 31--1aqe1--1HHX k nporpaMMa nega'raerr TOT xe pe3YJ1bTaT, T-ITO rpm k = 100 (BKJIK)qaa k = 100).

Бейсик

 

Алгоритмический язык

лм К, AS INTEGER INPUT К

12

WHILE F (I) > К

1

WEND

PRINT

FUNCTION F(N)

DIM 1, S AS INTEGER

1

       FOR                 1 ТО N

S

NEXT

END FUNCTION

 

алг нач цел К, i ввод К 1     12 нц пока F (i) > К i         1

вывод i кон алг цел F (цел п) нач     цел s ,

1 нц для i от 1 до п

кц знач кон

 

Python

def f (n) :

S   1 for i in range (1,

return s

К        int (input ( ) ) i       12 whi1e f (i) >k

1'—

print (i)

Ответ:

У исполнителя Калькулятор две команды:

1.  Прибавь 2,

2.  Умножь на З.

Первая из них увеличивает число на экране на З, вторая — удваивает его.

Программа для Калькулятора это последовательность ко манд. Сколько есть программ, которые число 2 преобразуют в число 42?

Ответ:

Сколько различных решений имеет уравнение

где А, В, С, D, Е — логические переменные?

В ответе не нужно перечислять все различные наборы значений А, В, С, D и Е, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.

Ответ:

Для записи ответов на задания 24—27 используйте бланк ответов NQ 2. Запишите сначала номер задания (24, 25 и т.д.), а затем полное решение. Ответы записывайте четко и разборчиво.

Часть 2

24. Требовалось написать программу, которая считывает с клавиатуры I натуральное число, которое не больше 10 9 , и выводит на экран сумму цифр, которые не кратны 5. Если таких цифр нет, программа должна вывести на экран О. Программист торопился и на-

писал программу неправильно.

 

Паскаль

Си

var х, sum, К integer; begin read1n.(x) ; sum о; whi1e х >= 10 do begin

К — х mod 10; if К mod 5 <> 0 then sum S ИТ + к; х х div 10 end; write1n (К) end.

#inc1ude <stdio.h> void main (void)

int х, sum, К; scanf        ,           ; sum = О; whi1e (х >= 10)

К          Х о if (К 0)

                sum       sum

х printf ( “     ,

Бейсик

 

 

Алго итмический язык

INPUT х sum

WHILE х                  10

         К            х MOD 5

IF К MOD 5

           sum          sum +

END х      х \ 10

WEND

PRINT к

о

К

THEN

алг нач

цел х, sum, К ввод х sum .

нц пока х >= 10 mod (х, 10) если mod (К, 5)

                sum            sum +

все х div (х, 10) кц вывод К кон

0 то

К

Python

 

 

 

х     int (input ( ) )

sum = 0 whi1e х >= 10 К       10 if К % 5 ! —

sum          sum х  х / / 10 print (К)

К

 

 

 

Бейсик

Паскаль

N=30

ЛМ А (М AS INTEGER лм Ш, Х, у AS INTEGER ЛМ S AS SINGLE

FOR                  1 ТО N

INPUT A(I) NEXT

END

const N=30; var а: array [1. .N] of integer; 1, х, у: integer;

S : rea1; begin for i:=1 to N do read1n (a [i] ) ;

end.

Си

Естественный язык

#inc1ude <stdio.h> #define N 30 void main (void) {int a[N] ; int i, х, У ; f10at S ; for (1=0; i<N; i++) scanf

Объявляем массив А из 30 эле— ментов .

Объявляем целочисленные пере— менные 1, Х, У.

Объявляем вещественную перемен— ную S .

В цикле от 1 до 30 вводим эле— менты массива А с 1—го по 30—й.

Python

20

None Ј None К None а [int (input ( ) ) for i 1 п range (N) ]

Последовательно выполните следующее.

1.                Укажите, что выведет на экран программа при вводе числа 1234.

2.                Приведите пример такого числа, при котором программа работает верно.

З. Исправьте все ошибки в программе. Для этого для каждой ошибки приведите строку, которая написана неверно, и строку, на которую ее нужно заменить, чтобы программа работала верно.

Дан целочисленный массив из 30 элементов. Элементы массива могут принимать целые значения от О до 1000 — баллы учащихся выпускного класса за итоговый тест по информатике. Опишите на русском языке или на одном из языков программирования алгоритм, который позволяет найти среднее арифметическое элементов массива, делящихся нацело на З. Известно, что в исходном массиве хотя бы один элемент делится нацело на З.

Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать часть из них.

В качестве ответа необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен на- ходиться на месте многоточия. Можно записать решение также на другом языке программирования (укажите название и используемую версию языка программирования, например Borland Pascal 7.0) или в виде блок-схемы. В этом случае вы должны использовать те же самые исходные данные и переменные, какие были предложены в условии (например, в образце, записанном на естественном языке).

26. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход - игрок может добавить в кучу 1 камень или 2 камня или увеличить количество камней в куче в З раза. Например, имея кучу из 6 камней, за один ход можно получить кучу из 7, 8 или 18 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 40. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 40 или больше камней.

В начальный момент в куче было S камней, 1 S 39.

Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

1.                а) При каких значениях числа S Петя может выиграть первым ходом? Укажите все такие значения.

б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

2.                Укажите два значения S, при которых у Пети есть выигрышная стратегия, причем Петя не может выиграть за один ход, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.

З. Укажите такое значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, но при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стра- тегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход, в узлах — количество камней в куче.

27. На вход программе подается набор символов, заканчивающийся  сиТволом О (в программе на языке Бейсик символы можно вводить по одному в строке; пока не будет введен ноль, или считывать данные из файла). Ноль в этом наборе единственный. Напишите эффективную, в том числе и по используемой памяти, программу (укажите используемую версию языка программирования, например Borland Pascal 7.0), которая будет составлять из всех имеющихся цифр (кроме завершающего последовательность  нуля) минимальное число, состоящее ровно из трех повторяющихся одинаковых групп цифр ненулевой длины. Составленное число следует вывести на экран или в файл.

В случае невозможности составить такое число, программа должна вывести «NO».

Например, пусть на вход подаются следующие символы: fd7s22hg 547h2j 47х5 540

В данном случае программа должна вывести:

245724572457

ОТВЕТЫ К ДИАГНОСТИЧЕСКОМУ ВАРИАНТУ ЭКЗАМЕНАЦИОННОЙ РАБОТЫ

задания

Ответ

Л) задания

Ответ

Л) задания

Ответ

1

 

11

56

21

64

2

зо

12

ГБВА

22

15

з

587

13

250

23

зо

4

з

14

2

 

5

9

15

18

6

3959

16

2017

7

36

17

14

8

32

18

85

9

4

19

8

10

лкмкк

20

159

24

Содержание верного ответа и указания по оцениванию

(допускаются иные формулировки ответа, не искажающие его смысла)

Решение использует запись программы на Паскале. Допускается использование программы на трех других языках.

1.  Программа выведет число: 2.

2.  Пример числа, для которого программа работает правильно: 1513.

Замечание для проверяющего. Вместо суммы цифр, не кратных 5-ти программа выводит на экран вторую по счету. Значит, верным будет любое число, у которого сумма цифр, не кратных 5-ти, равна второй по счету цифре. З. В программе есть две ошибки.

Первая ошибка: неверное условие окончания цикла. Строка с ошибкой: while х >= 10 do Верное исправление: while х > О do

Вторая ошибка: неверный вывод на экран.            Строка с ошибкой: writeln(k)

Верное исправление: writeln(sum) 

 

Указания по оцениванию

Баллы

Обратите внимание! В задаче требовалось выполнить четыре действия:

1)                 указать, что выведет программа при конкретной входной последовательности;

2)                 указать пример последовательности, при которой программа работает правильно; З) исправить первую ошибку; 4) исправить вторую ошибку.

Для проверки правильности выполнения п. 2) нужно формально выполнить исходную (ошибочную) программу с входными данными, которые указал экзаменуемый, и убедиться в том, что результат, выданный программой, будет таким же, как и для правильной программы.

 

Для действий З) и 4) ошибка считается исправленной, если выполнены оба следующих условия:

а) правильно указана строка с ошибкой;

б) указан такой новый вариант строки, что при исправлении другой ошибки получается правильная программа

 

Выполнены все четыре необходимых действия, и ни одна верная строка не указана в качестве ошибочной

З

Не выполнены условия, позволяющие поставить З балла. Имеет место одна из следующих ситуаций:

а) выполнены три из четырех необходимых действий. Ни одна верная строка не указана в качестве ошибочной;

б) выполнены все четыре необходимых действия. Указано в качестве ошибочной не более одной ве ной строки

2

Не выполнены условия, позволяющие поставить 2 или З балла. Выполнены два необходимых действия из четырех

1

Не выполнены условия, позволяющие поставить 1, 2 или З балла

 

Максимальный балл

 

25

Возможные варианты ответа:

Бейсик

 

Паскаль

FOR      1 ТО N о х=Х+1

У=У+А (1)

ENDIF

NEXT

PRINT S

THEN

х:=О;

for i :=1 to N do if (A[i] mod З 0) then begin

end;

s:=y/x;      write1n

Си

 

Естественный язык

for (i=O; i<N;

х=х+1;

 (f10at) у / х; printf , S )

i++)

0)

Записываем в переменные Х и У нулевые значения . В цикле от первого элемента до тридцатого проверяем делимость элементов массива на З. Если остаток от де— ления текущего элемента на З равен 0, то увеличиваем значение переменной Х на 1, а значение переменной У на значение этого элемента. Переходим к следующему элементу массива .

После завершения цикла вычисляем значение среднего арифметического, деля У на Х и записывая результат в S . Выводим значение переменной S .

 

 

Python

х=0 for     in range (1,N) :

х=х+1

s=y/x print (s)


26

Содержание верного ответа и указания к оцениванию

(допускаются иные формулировки ответа, не искажающие его смысла)

1а) S = 14...39. Петя должен увеличить количество камней в куче в З раза и выиграть. Для S < 14 невозможно одним ходом получить в куче 40 и более камней.

16) S = 13. Куда бы ни пошел Петя (13 + 1 — 14, 13 + 2 = 15 Или 13*3 = 39), Ваня должен увеличить количество камней в куче в З раза и выиграть.

2. S = 11 и S = 12. Своим первым ходом Петя должен получить в куче 13 камней (11 + 2 = 13 или „12 + 1 13). При любом ответном ходе Вани (13 + 1 14, 13 + 2 = 15 или 13*3 = 39), Петя должен увеличить количество камней в куче в З раза и выиграть.

З. S = 10. Если Петя утроит количество камней в куче (10*2 = 30), Ваня должен также утроить количество камней в куче и выиграть (30*3 = 90).

Если же Петя добавит в кучу 1 или 2 камня (10 + 1 11 или 10 + 2 = 12), Ваня получит в куче 13 камней (11 + 2 = 13 или 12 + 1 13). При любом ответном ходе Пети (13 + 1 = 14 , 13 + 2 = 15 или 13*3 = 39) Ваня должен увеличить количество камней в куче в З раза и выиграть. Рассмотрим дерево игры:

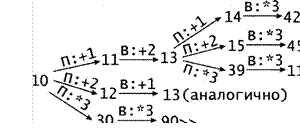
В этом дереве в каждой позиции, где должен ходить Петя, разобраны все возможные ходы, а для позиций, где должен ходить Ваня — только ход, соответствующий стратегии, которую выбрал Ваня.

27

Основные элементы правильного ответа:

Программа читает все входные данные только один раз, запоминая в целочисленном массиве из 9 элементов, сколько раз встречается соответствующая цифра во входных данных.

После этого проверяется, что все ненулевые элементы этого массива равны трем. Если это условие не выполняется или все элементы массива равны нулю, то выводится «NO».

В противном случае три раза подряд выводится упорядоченная по возрастанию группа цифр, состоящая из всех ненулевых цифр исходной строки.

Пример возможного решения (на С++):

#inc1ude <iostream> using namespace std; int main ( ) int пит [10] ; / / из соображений наглядности элемент пит [0] не задействован

char с; for (int i=1; i<=9; cin >> с; whi1e (с ! —

cin >> с;

пит [ i j        о; / / инициализация

пит [с— '/ / подсчет цифр

Ьоо1 yes =fa1se; for (int i=1; i<=9; i++)

/ / проверка, есть ли в строке хотя бы одна цифра if yes — true; break;

if (yes)

for (int i=1; i<=9; i++)

/ / проверка, кратно ли трем количество вхождений каждой встреченной цифры if О ) && (num[i] %3!= yes fa1se; break;

(yes) / / вывод результата

for (int ј=1; Ј<=3; Ј++) for (int i=1; i<=9; for (int К=1; К<= пит [i]cout << i ;

e1se cout << cout << ' \n ' ; return 0;

Пример возможногЬ решения (на классическом Паскале): program с4 (input, output) ; var пит: array [ 1 of integer; i, c : char; j , k: integer; yes : Ьоо1еап;

begin

 

 

for ' 1 ' to   read (с) ; whi1e с <> ' 0 ' do begin   

do num[i]             о; { инициализация

 

if (с>—'— 1 ' ) read (с) end;

and (с<=' 9 ' ) then пит [с]                 пит [с] +1;

{ подсчет цифр }

               yes       fa1se;

whi1e (not yes) and (i<=' 9' ) do begin

{проверка, есть ли в строке хотя бы одна цифра} if num[i) > 0 then yes true; i:— succ (i) end; if yes then begin i := whi1e yes and  do

{ проверка, кратно ли трем количество вхождений каждой встреченной цифры} begin if (num[i] and (пит [1] mod З <>O) then yes fa1se; i:— succ (i)

end; if yes then {BblBOA pe3YJ1bTana} begin for j : = 1 to 3 do for i: = ' 1 ' to ' 9' do for k:=l to num [i] div 3 do write (i)

else write ( 'NO' ) ; write In;

Ilpumep 603MO%HOeo peuuua (Ha Beücuxe, wounungmop FreeBASIC):

Dim num (9) As Integer

Dim i As Integer

Dim j As Integer

Dim k As Integer

Dim yes As Integer

Dim c As String

For To 9 Num (i) 0

Next i

Input c

Do While

' 110AcqeT I-ILOp if (c>" 0" ) And (c<—''9' Then Num (Asc (c) —Asc (  Num (Asc (c) — Asc ( Input c Loop

yes

For     To 9

' npoBepKa, ec tTb B c rrpore 6b1 OAHa I-LIOpa

If num (i) > 0 Then yes 1

Exit For

End If Next i

If yes   1 Then

For    To 9 npoBepKa, I-cpaTH0      rrpeM KOJImqeCTBO BXoxmeHMJ51 Kaxmolh BcnpeqeHHoV1

If (num (i) >0) And (num (i) Mod 3<> 0) Then yes

Exit For

End If

Next

End If

If yes       1 Then ' BblB011 pe3YJ1b rra rra

            For      To 3

                        For     To 9

For k=l To num (i) / 3 c=c+Chr$ (i+Asc ('

Next k

Next i

Next j

Print c

Else

Print "NO"

End If

1. КОЛИЧЕСТВО ИНФОРМАЦИИ.

СКОРОСТЬ ПЕРЕДАЧИ ИНФОРМАЦИИ

Основные понятия

Информация первичное понятие, не имеющее общепринятого, классического определения. Одно из возможных определений: сведения об окружающем нас мире.

Для измерения информации используются специальные единицы: бит, байт, килобайт, мегабайт, гигабайт и т.д.

Минимальной (и основной) единицей измерения информации является один бит. Бит — количество информации, которое уменьшает неопределенность в два раза.

Другое определение:

Бит количество информации, необходимое для передачи сообщения «Да» / «Нет» . Бит может принимать только два возможных значения. Обычно их обозначают «1» и «О».

Восемь бит составляют один байт.

Для обозначения больших единиц измерения информации используются префиксы кило-, мега-, гига- и другие, например килобайт, мегабайт, гигабайт. Однако в отличие от обще-

признанных значений префиксов («кило-» 103 , «мега-» — 106 , «гига-» — 109 ) при использовании их применительно к битам и байтам они обозначают близкие степени «двойки»: «киЛО- » = 2 10 , «мега-» = 220, «гига-» = 2 30 . То есть

1024 байт = 1 килобайт (Кбайт, кб)

1024 килобайт = 1 мегабайт (Мбайт, Мб)

1024 мегабайт 1 гигабайт (Гбайт, Гб)

В действительности, под терминами «килобайт», «мегабайт», «гигабайт» правильнее понимать именно 103 , 106 , 109 . Но в ЕГЭ вместо этих терминов используются обозначения Кбайт, Мбайт, Гбайт, которые (для правильного решения задач ЕГЭ) следует принимать именно как 2 10 , 2 20 , 230 байт.

Для вычисления количества информации применяют несколько различных способов, в зависимости от ситуации.

*         Для вычисления количества информации в сообщении об одном из равновероятных событий, общее количество которых равно N, используйте формулу:

где • — количество информации в сообщении.

*         Для вычисления количества информации в сообщении об одном из неравновероятных событий, вероятность которого равна р, используйте формулу: i = —Подо], где i — количество информации в сообщении, квадратные скобки обозначают ближайшее целое, меньшее или равное значению выражения в скобках.

*         Для вычисления количества информации в сообщении из К символов некоторого алфавита, в котором N различных знаков, используйте формулу:

где I — количество информации в сообщении, i — найти из формулы 2 = N.

Скорость перёдачи информации измеряется в битах в секунду и вычисляется по формуле:

где — скорость передачи информации, I — количество информации в сообщении, t — время передачи сообщения.

Практическая часть

1.1. Выберите правильные определения термина «бит» (обведите буквы, соответствующие правильным определениям):

                    а) бит       минимальная единица измерения информации

б) бит равен одной восьмой части байта

в) бит это количество информации, которое уменьшает неопределенность в два раза

г) бит может принимать только два значения — О или 1

                   д) бит      основная единица измерения информации

е) бит — количество информации, необходимое для передачи сообщения «Да» / «Нет»

1„2. В списке утверждений предыдущей задачи поставьте «галочки» перед утверждениями,             которые являются верными, но не являются определениями термина «бит».

Напоминание. Основная формула для расчета количества информации (бит):

где N — количество равновероятных событий, i — количество информации в сообщении об одном из этих событий.

1.3. Подбрасывают монетку. Она может упасть орлом или решкой. Какое количество информации в сообщении о том, что выпал орел (в битах)?

Загадали число от 1 до 8. Какое количество информации в сообщении о том, какое число загадано (в битах)?

Замечание. Если ответ получается не целый, выберите следующее целое число (пример: если получается 2,16 бит, ответ: З бита). Обычно (на всякий случай) в задании это специально оговаривается. Если это не указано, надо выбрать ближайшее целое сверху.

Другими словами, основную формулу для расчета количества информации (2 = N) правильнее было бы записать так: наименьшее целое i такое, что 2l 2 N.

1„5. Бросили шестигранный игральный кубик. Какое количество Информации в сообщении о том, какое число выпало на кубике (в битах)?

1-6. Загадано число от 1 до 100. Загадавший на все вопросы отвечает только «Да» или «Нет». Какое наименьшее число вопросов нужно задать, чтобы гарантированно угадать число?

1.7. Для обмена сообщениями используют последовательности символов одинаковой длины, состоящие только из символов «А» и «В». Какова должна быть минимальная длина этих последовательностей, чтобы каждая из них кодировала любое из 50 различных сообщений?


1.8. Световое табло состоит из лампочек, каждая из которых может находиться в двух состояниях («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 200 различных сигналов?

Напоминание. Если имеется сообщение, состоящее из символов некоего алфавита (и все символы алфавита равновероятны), то количество информации в сообщении (I) вычисляется по формуле:

где • — количество информации в одном символе алфавита, К — количество символов в сообщении.

1.9. Эллочка-людоедка (в лексиконе которой, как известно, было 30 слов) произносит фразу, состоящую из 50 слов. Какое количество информации в битах сообщает Эллочка?

1.10. В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого  спортсмена. Каков информационный объем в битах сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов?

1.11. Репетиционный экзамен в школе сдают 125 человек. Каждому из них выделяют специальный номер, идентифицирующий его в автоматической системе проверки ответов. При регистрации участника для записи его номера система использует минимально возможное количество бит, одинаковое для каждого участника. Каков объем информации в битах, записанный устройством после регистрации 60 участников?

1.12. Для передачи секретного сообщения используется код, состоящий из десятичных цифр.  При этом все цифры кодируются одним и тем же (минимально возможным) количеством бит. Определите информационный объем в битах сообщения длиной в 150 символов.

1.13. Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от О до 100 процентов, которое записывается при помощи минимально возможного количества бит. Станция сделала 80 измерений. Определите информационный объем в битах результатов наблюдений.

1.14. Для записи результатов детской игры «Зарница» используется таблица, в каждой клетке которой записано либо количество баллов, полученных командой в соответствующем виде состязаний (1, 2, З), либо прочерк (если команда в этом виде соревнований не участвовала). В «Зарнице» соревнуются 30 команд в 10 видах соревнований. Какое количество информации в битах содержит таблица?

Напоминание. Для вычисления скорости передачи информации нужно поделить количество передаваемой информации (в битах) на время передачи информации (в секундах). То есть скорость передачи информации измеряется в битах в секунду.

где I — количество информации в ггередаваемом сообщении (в битах), t — время передачи этого сообщения (в секундах), v — скорость передачи информации (бит в секунду).

1.15. Вася передает Пете сообщение, состоящее только из символов (заглавных и строчных) латинского алфавита, пробелов и знаков препинания (. , ! ? ) за 2 минуты. Сообщение состоит из 200 символов. Какова скорость передачи информации (бит в секунду)?

1.16. Вождь племени Мумба-Юмба, в лексиконе которого всего 64 различных слова, произносит пламенную речь перед своими соплеменниками, состоящую из 100 слов в течение 2 минут. Какова скорость передачи информации (бит в секунду)?

ответ:

1.17. Флажковый сигнальщик использует для передачи сообщения 36 различных жестов (комбинаций флажков). Сообщение, состоящее из 50 жестов, сигнальщик передает за полминуты. Какова скорость передачи сообщения (бит в секунду)?

Ответ:

Напоминание. Более крупными единицами измерения информации являются:

1 байт = 8 бит

1 килобайт = 1024 байт = 2 10 байт 1 мегабайт = 1024 килобайт = 220 байт

1  гигабайт = 1024 мегабайт = 230 байт

1.18.  Сколько килобайт информации содержит сообщение объемом 2 24 бит?

Ответ:

1.19.  Сколько килобит информации содержит сообщение объемом 214 байт?

Ответ:

1.20.  Во время передачи кабельного телевидения автоматизированная система собирает информацию от телезрителей относительно фильма, который они хотели бы посмотреть вечером. На выбор предлагается 4 фильма. Для кодирования каждого пожелания система использует минимально необходимое количество бит. Всего высказали свои пожелания 102 400 телезрителей. Какое количество килобайт должна проанализировать система?

Ответ:

1.21.  Скорость передачи данных через равна 128 ООО бит/с. Через данное соединение передают файл размером 625 Кбайт. Определите время передачи файла в секундах.

Отв т:

Рекомендация. Эту задачу можно решать просто по размерности. Имеются биты/сек и Кбайты. Нужно получить секунды. Значит, нужно Кбайты поделить на биты/сек. Запишите эти величины в виде дроби. Чтобы числитель и знаменатель были одинаковой размерности, используйте 2 10 чтобы «избавиться» от приставки «кило» (кило - 2 10) и 23 , чтобы перевести байты в биты (1 байт = 8 бит). Сократите числитель и знаменатель на нужные степени «двойки». Посчитайте

результат.

1„22. Саша хочет скачать из Интернета видеоролик, объем которого 240 Мбит. Единственный способ это сделать — на перемене. Но, к сожалению, в этот момент канал пере гружен и скорость скачивания файла ограничена 16 килобайтами/сек. Сколько минут потребуется Саше?

1„23. Через канал связи со скоростью 50 Кбит/с передают файл объемом З 072 ООО байт. Сколько минут будет передаваться файл?

1.24. Через канал связи со скоростью 64 Кбайт/с передают файл в течение 10 минут. из скольких мегабайт состоит файл?

1„25. Скорость передачи данных через  равна 256 ООО бит/с. Передача файла через это соединение заняла 2 минуты. Определите размер файла в килобайтах.

Напоминание. Кодирование информации не обязательно должно быть двоичным. Можно использовать не два различных состояния (ноль и один), а больше, в зависимости от выбранного способа передачи / хранения информации. Например: фонарики трех различных цветов, палочки четырех различных длин, символы из некоторого алфавита. Количество информации при этом будет рассчитываться, конечно, по тем же формулам, что описано выше. Но вы должны таюке уметь рассчитывать, как кодировать сообщение, используя данные способы кодирования. Для этого используется формула:

где К — количество различных сигналов (лампочек символов / объектов), которые используются при кодировании, s — длина последовательности этих сигналов,

N — количество различных сообщений, которое можно закодировать, используя последовательность из s сигналов различных видов.

Если необходимо закодировать количество сообщений, не являющееся целой степенью числа К (различных сигналов), нужно взять ближайшее целое сверху (то есть такое наименьшее целое s, чтобы выполнялось: кд > N).

1.26. Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?

Ответ:

Рекомендация. Здесь количество различных используемых сигналов— количество состояний лампочки — З, количество сообщений — 18.

1-27. Азбука Морзе позволяет кодировать символы для радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т.д.) можно закодировать, используя код Морзе длиной не менее пяти и не более шести сигналов (точек и тире)?

Ответ:

Рекомендация. Так как сообщения длиной 5 и длиной 6 сигналов можно кодировать независимо одни от других (они отличаются длиной), нужно по отдельности посчитать число различных 5-символьных и 6-символьных сообщений и сложить результаты.

1.28. Вася и Петя передают друг другу сообщения, используя синий, красный и зеленый фонарики. Это они делают, включая по одному фонарику на одинаково короткое время в некоторой последовательности. Количество вспышек в одном сообщении З или 4. Между сообщениями — паузы. Сколько различных сообщений могут передавать мальчики?

Ответ:

1.29. Для кодирования ЗОО различных сообщений используют 5 последовательных цветовых вспышек. Вспышки одинаковой длительности, для каждой вспышки используется одна лампочка определенного цвета. Лампочки скольких различных цветов должны использоваться при передаче (минимально возможное количество)?

Ответ:

1.30. В некоторой организации решили присвоить каждому сотруднику уникальный код, состоящий из символов латинского алфавита (используются все 26 заглавных букв) и цифр. При этом сначала записываются З латинских символа, а потом — 5 цифр. Код

зо

каждого сотрудника хранится в компьютерной программе при помощи минимально возможного количества байт. При этом используется посимвольное кодирование и каждый символ кодируется одинаковым и минимальћо возможным количеством бит. То же для цифр — каждая цифра кодируется одинаковым и минимально возможным количеством бит. Определите объем памяти (в байтах), необходимый программе для записи кодов 64 сотрудников.

Рекомендация. Посчитайте отдельно количество информации, которое требуется для одного символа (всего имеется 26 возможных) и для одной цифры (всего имеется 10 возможных). Это нужно сделать по формуле 2 = N. Умножьте первый результат на число символов в коде (З), а второе — на число цифр в коде (5). Результаты сложите. Получится количество бит, требуемое для кодирования одного кода. Так как каждый код хранится байтами, найдите наименьшее число байт, в котором поместится столько бит (наименьшее целое, которое не меньше чем результат деления на 8). Это число умножьте на количество сотрудников.

1.31. В некотором университете решили ввести единую нумерацию всех помещений. Каждому помещению поставили в соответствие номер, состоящий из трех частей. Первая часть буква здания факультета (заглавная буква, одна из 6). Вторая часть — номер этажа, на котором находится аудитория (цифра от 1 до 5). Третья часть — номер аудитории на этаже (число от 1 до 40). Номер каждой аудитории хранится в компьютерной программе при помощи минимально возможного количества байт. При этом каждая часть кодируется отдельно одинаковым и минимально возможным количеством бит. Определите объем памяти (в байтах), необходимый программе для записи кодов 400 аудиторий.

1.32. У Кати появился скоростной доступ в Интернет. Это позволяет ей получать из Интернета файлы со скоростью 2 22 бит в секунду. Ее соседка через дорогу Маша договорилась с Катей, что сможет получать от нее файлы по прямому оптическому каналу со скоростью 2 17 бит в секунду. Маше нужно скачать файл объемом 5 Мбайт. При этом особенности передачи таковы, что Катя должна сначала получить из Интернета первую часть файла объемом 1 Мбайт и только потом сможет начать передавать файл Маше. Через какое количество секунд от начала получения файла Катей Маша сможет получить весь заказанный файл? В ответе укажите только число.

Рекомендация. Из-за необходимости передать Кате сначала первую часть файла, время передачи разбивается на две части: время, необходимое для получения Катей первой части файла, и время, необходимое для получения Машей всего файла от Кати. В первом случае передается 1 Мбайт со скоростью 222 бит в секунду. Делим первое на второе и не забываем уравнять размерности. Например, переводим все в байты. Числитель умножаем на 220 (число байт в мегабайте), знаменатель делим на 23 (число бит в байте). Аналогично вычисляем вторую величину: делим 5 Мбайт на 217 бит в секунду. Не забываем уравнять размерности. Складываем числа, полученные в результате обоих делений.

1.33. У Кати появился скоростной доступ в Интернет. Это позволяет ей получать из Интернета файлы со скоростью 220 бит в секунду. Ее соседка через дорогу Маша договорилась с Катей, что сможет получать от нее файлы по прямому оптическому каналу со скоростью 2 18 бит в секунду. Маше нужно скачать файл объемом 8 Мбайт. При этом особенности передачи таковы, что Катя должна сначала получить из Интернета первую часть файла объемом 512 кбайт и только потом сможет начать передавать файл Маше. Через какое количество секунд от начала получения файла Катей Маша сможет получить весь заказанный файл? В ответе укажите только число.

1.34. Документ объемом 20 Мбайт можно передать с одного компьютера на другой двумя способами:

А. Сжать архиватором, передать архив по каналу связи, распаковать.

Б. Передать по каналу связи без использования архиватора. Какой способ быстрее и насколько, если:

средняя скорость передачи данных по каналу связи составляет 2 20 бит в секунду; объем сжатого архиватором документа равен 20 0/0 исходного; время, требуемое на сжатие документа, 5 секунд, на распаковку — 1 секунда? В ответе напишите букву А, если быстрее способ А, или Б, если быстрее способ Б. Сразу после буквы напишите число, обозначающее, на сколько секунд один способ быстрее другого.

 Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б2З.

Единиц измерения «секунд», «сек», «с» к ответу добавлять не нужно.

Рекомендация. Посчитаем время, требуемое для каждого способа. Сначала посчитаем время, требуемое для способа Б. По формуле это объему деленный на скорость. Уравняем размерности для числителя и знаменателя. Например, приведем все в битах. Получаем: 20 * 2 23 [220 = 160 секунд. Теперь посчитаем время, требуемое для способа А. Так как объем сжатого файла составляет 20 0/0 исходного, то и время передачи файла составит 200/0 от времени передачи несжатого файла. Получаем 5 секунд на сжатие, еще  на передачу, еще 1 секунда на распаковку. Всего 5 + + 1 = 5 + 32 + 1 = 38 сеюунд. Это быстрее, чем 160 секунд, на 122 сеюунды (= 160 — 38). Значит, ответ запишем как А 122.

1.35. Документ объемом 16 Мбайт можно передать с одного компьютера на другой двумя способами:

А. Сжать архиватором, передать архив по каналу связи, распаковать.

Б. Передать по каналу связи без использования архиватора. Какой способ быстрее и насколько, если:

средняя скорость передачи данных по каналу связи составляет 2 22 бит в секунду; объем сжатого архиватором документа равен 25 0/0 исходного; время, требуемое на сжатие документа, — 8 секунд, на распаковку — З секунды?

32

В ответе напишите букву А, если быстрее способ А, или Б, если быстрее способ Б. Сразу после буквы напишите число, обозначающее, на сколько секунд один способ быстрее другого.

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б2З.

Единиц измерения «секунд», «сек», «с; к ответу добавлять не нужно.

1.36. Документ объемом 30 Мбайт можно передать с одного компьютера на другой двумя способами:

А. Сжать архиватором, передать архив по каналу связи, распаковать.

Б. Передать по каналу связи без использования архиватора.

Какой способ быстрее и насколько, если:

средняя скорость передачи данных по каналу связи составляет 2 24 бит в секунду; объем сжатого архиватором документа равен 40 0/0 исходного; время, требуемое на сжатие документа, — 8 секунд, на распаковку — 4 секунды? В. ответе напишите букву А, если быстрее способ А, или Б, если быстрее способ Б. Сразу после буквы напишите число, обозначающее, на сколько секунд один способ быстрее другого,

Так, например, если способ Б быстрее способа А на 23 секунды, в ответе нужно написать Б2З.

Единиц измерения «секунд», «сек», «с» к ответу добавлять не нужно.

1.37. Вася составляет 5-буквенные слова, в которых есть только буквы С, Л, О, Н, причем буква С используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная.  Сколько существует таких слов, которые может написать Вася?

Рекомендация. Буква С встречается ровно 1 раз. Она может стоять на 5-ти возможных позициях. Расстановка буквы С никак не влияет на расстановку оставшихся букв на оставшихся 4-х позициях. На каждую из этих 4-х позиций можем поставить любую из 3-х букв. Это 34 = 81 комбинация. Это количество умножаем на число способов расставить букву С. То есть 81*5 = 405 вариантов.

1.38. Вася составляет 4-буквенные слова, в которых есть только буквы Ж, И, Р, А, Ф, причем буква Ж используется в каждом слове ровно 1 раз. Каждая из других допустимых, букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

1.39. Вася составляет 4-буквенные слова, в которых есть только буквы В, А, С, Я, причем буква Я используется в каждом слове ровно 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может написать Вася?

1.40. Вася составляет 4-буквенные слова, в которых есть только буквы Г, В, О, З, Д, Ь, причем буква Г используется в каждом слове ровно 1 раз. Каэкдая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Словом считается любая допустимая последовательность букв, не обязательно осмысленная. Сколько существует таких слов, которые может. написать Вася?

1.41. При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 15 символов и содержащий только символы из 12-символьного набора: А, В, С, D, Е, Р, G, Н, К, L, М, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При

этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт на одного пользователя. Определите объем памяти (в байтах), необходимый для хранения сведений о 50 пользователях. В ответе запишите только целое число количество байт.

Рекомендация. Найдем количество информации в одном символе. Так как всего возможно 12 символов, по формуле Хартли имеем 2 2 12 => i = 4 бита. Всего в пароле 15 символов. По формуле • 15*4 = 60 бит. Так как для каждого пользователя хранится дополнительно 12 байт, всего получаем 60 бит + 12 байт. Так как в базе для пользователя отведено целое количество байт, переводим биты в байты. 60/8 = 7,5. Это помещается в 8 байт. Итого 8 + 12 = 20 байт на одного пользователя. Всего 50 пользователей. Значит, 20*50 = 1000 байт.

1„42. При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 13 символов и содержащий только символы из 10-символьного набора: А, В, С, D, Е, Р, G, Н, К, L. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 8 байт на одного пользователя. Определите объем памяти (в байтах), необходимый для хранения  сведений о 40 пользователях. В ответе запишите только целое число -2— количество байт.

1.43. При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 15 символов и содержащий только символы из 6-символьного набора:  А, В, С, D, Е, Р. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 14 байт на одного пользователя. Определите объем памяти (в байтах), необходимый для хранения сведений о 25 пользователях. В ответе запишите только целое число — количество байт.

1-44. При регистрации в компьютерной системе каждому пользователю выдается пароль, состоящий из 9 символов и содержащий только символы из 13-символьного набора: А, В, С, D, Е, Р, G, Н, К, L, М. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 10 байт  на одного пользователя. Определите объем памяти (в байтах), необходимый для хранения сведений о 60 пользователях. В ответе запишите только целое число — количество байт.

2. СИСТЕМЫ СЧИСЛЕНИЯ

Основные понятия

Система счисления (ССч) набор знаков, используемых для записи чисел и правила записи чисел. Эти знаки называются цифрами.

Набор этих цифр называется алфавитом системы счисления.

Количество цифр в алфавите называется мощностью алфавита.

Различают позиционные и непозиционные системы счисления.

Если для каждого числа системы счисления выполняется правило: вес цифры (ее значение) зависит от положения цифры в числе, такая система счисления называется позиционной. Если хотя бы для одного числа это правило не выполняется, система счисления называется непозичионной.

Пример непозиционной системы счисления — римская. В ней для числа II вес каждой цифры одинаков (равен единице).

Количество цифр в позиционной системе счисления называется основанием системы счисления. Именно во столько раз вес каждого разряда больше веса соседнего.

Основание — основная характеристика позиционной системы счисления.

Система счисления, которой мы пользуемся в повседневной жизни и которую изучаем в школе, десятичная позиционная. Десятичная — потому что в ней используется десять цифр для записи чисел (от «О» до «9»), и именно в десять раз вес каждого разряда отличается от соседнего (вес сотен в десять раз больше веса десятков).

Самое маленькое основание позиционной системы счисления — 2.

Это самая простая система счисления для записи чисел, в ней всего два знака — «1». Поэтому именно двоичная система счисления используется для хранения чисел в компьютере.

Если нужно записывать числа в системе счисления, основание которой больше 10, привычных арабских цифр (от О до 9) не хватает и принято использовать буквы латинского алфавита: десять — А, одиннадцать — В и т.д.

Обычно используется 16-теричная система счисления.

При записи чисел в различных системах счисления принято записывать основание системы счисления справа внизу возле числа. Например, число 6 в восьмеричной системе счисления записывают: 68. Если основание системы счисления справа внизу возле числа не указано, считается, что это десятичная система счисления.

Для перевода числа из какой-либо системы счисления в десятичную необходимо:

1)    пронумеровать разряды числа справа налево, начиная с нуля;

2)    умножить каждую цифру числа на основание его системы счисления, возведенное в степень номера этого разряда;

З) сложить полученные числа.

Для перевода десятичного числа в другую систему счисления необходимо:

1)    делить нацело с остатком число на нужное основание системы счисления;

2)    получившееся частное (целое) тоже делить нацело с остатком на это основание; З) продолжать деления до тех пор, пока частное не получится равно нулю; 4) выписать остатки в порядке, обратном их получению.

Практическая часть

2.1.        Расставьте необходимые термины напротив их определений.

Термины: система счисления, алфавит системы счисления, мощность алфавита, основание системы счисления.

                             а) количество цифр, используемых при записи чисел

б) набор цифр, используемых при записи чисел, и правила записи чисел

                             в) правила записи цифр

                             г) набор цифр, используемых при записи чисел

д) количество цифр в алфавите позиционной системы счисления

2.2.        Чем отличается позиционная система счисления от непозиционной?

Ответ:

2.3.       


В позиционной системе счисления во сколько раз вес (значение) каждого разряда больше предыдущего?

 Ответ:

2.4.        В  системе счисления для записи чисел используется различных цифр. Самая маленькая цифра равна Самая большая цифра равна

2.5.        В  системе счисления число, которое на 1 больше, чем самая старшая цифра, записывается как

2.6.        В двоичной системе счисления для записи чисел используются только           и         

2.7.        В шестнадцатеричной системе счисления кроме обычных десяти арабских цифр (от О до 9) используются также букв латинского алфавита: от до Цифра «десять» записывается как , цифра « » записывается как F.

2.8, Обозначьте на рисунке следующие термины (обведите и подпишите или напишите термин и стрелками укажите их): разряд, номер разряда, основание системы счисления.

4 3 2 1 0

5 2 43 68

2.9.            В шестнадцатеричной системе счисления между числами 2В16 и 2Е16 находятся числа

16 и 16.

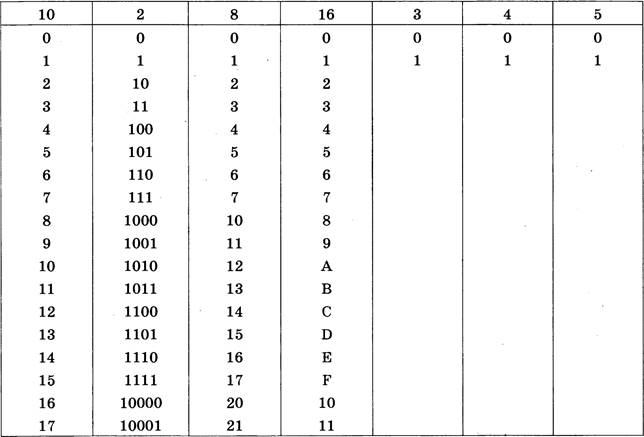
2.10.       Заполните пустые клетки таблицы последовательными числами в системах счисления с основанием З, 4, 5 (таблицу соответствия между десятичной, двоичной и шестнадцатеричной системами счисления мы рекомендуем вам выучить наизусть).

Система счисления

2.11.       После числа:           1001112          2123    378      213334            667

следует число:

         2• 12 Числу:                       101002           21003             5208           АОО16          31204              507

предшествует число:         

2.13.       Между числами:           BF16 и С11б 22213 и 100003       10916 и 10В16

                               стоит число:                                                                  16                                                           16

2.14.       В каждом столбце обведите большее число и подчеркните меньшее:

100102201035078АОО1б1000041FF16

111232778EOF16300004F0016

10100222123374810D1623012433316

110002122236308CFF16321004АВС16

2.15.       Расставьте цифры порядок выполнения действий при переводе из любой системы счисления в десятичную:

сложить все числа пронумеровать разряды числа справа налево, начиная с нуля цифру каждого разряда умножить на основание системы счисления, возведенное в степень номера разряда

2.16.       Расставьте цифры порядок выполнения действий при переводе из десятичной системы счисления в любую другую:

выписать остатки от деления слева направо в порядке, обратном их получению повторять действие до тех пор, пока частное от деления не будет равно нулю поделить число нацело с остатком на основание системы счисления, в которую переводим

Напоминание. При переводе из двоичной системы счисления в десятичную цифры, которые нужно умножать на число 2 в какой-то степени, равны 0 или 1. Все, что умножено на 0, все равно дает ноль. Поэтому эти слагаемые лучше просто опустить. Все, что умножено на 1, таким же и остается. Поэтому эти умножения тоже лучше опустить. Получается, достаточно просто сложить степени «двойки», в разрядах которых стоят «единицы».

2.17.       Переведите числа в десятичную систему счисления (заполните пропущенные в клетках цифры):

         23 14$        5 3 + 3 510

паз

                 2 А Д16 162 + 10                                                512 + Пб

2.18.       Переведите числа в десятичную систему счисления:

10101102

            210203

5268

ЗСЕ16

30214

2567

для успешного выполнения следующих заданий по системам счисления необходимо хорошо помнить материал младшей школы.

2.19.       Выполните деление в целых числах:

47

7

 

 

 

 

            То есть 47 делить на 7, получится         целых и         в остатке.

2.20.       23 делить на 5, получится         целых и         в остатке.

2.21.       7 делить на 9, получится           целых ив остатке.

222. Переведите число 53 в двоичную систему счисления:

2.23. Переведите число 202 в пятеричную систему счисления:

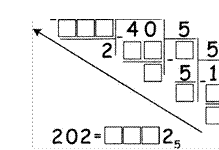
2.24. Переведите числа в указанные системы счисления:

5710

6510

33510

20210

19810

13910

 

з

8

16

4

7

2

Замечание. При переводе десятичного числа в двоичную систему счисления можно воспользоваться более быстрым способом (хотя и более ненадежным, с точки зрения вероятности ошибки). Разложить исходное число на сумму степеней двойки (от большей к меньшей), после чего поставить единицы в те позиции двоичного числа, степени которых присутствуют в этой сумме. Остальные позиции заполнить нулями:

83 = 64 + 19 = 64 + 16 +3 = 64 + 16 + 2 + 1 = 26 + 24 + 2 1 + 20 = 10100112

Получив сумму степеней «двойки» рекомендуем такой прием: начинаем про себя называть степени двойки, с самой старшей (в данном примере с шести), по убывающей, подряд, до нуля. для каждой названной степени записываем друг за другом цифры: «1» — если такая степень есть в сумме, или «0» — если такой степени нет.

В данном примере д.пя степеней 6, 4, 1 и О записали «1», а для 5, З и 2 — «О».

для эффективного использования этого метода необходимо наизусть знать степени числа «2». Вообще говоря, это знание очень поможет вам решать множество задач ЕГЭ по информатике. Мы рекомендуем заранее выучить степени двойки хотя бы до 10-й, а лучше — до 16-й.

Напоминание. Две системы счисления будем называть родственными, если основание одной системы счисления равно степени основания другой. Например, 2 и 8, 2 и 16, З и 9.

для произвольной пары систем счисления, чтобы перевести число из одной системы в другую, нужно осуществлять два перевода — сначала из исходной в десятичную, потом из десятичной в нужную. В родственных системах счисления можно осуществлять перевод напрямую. Чтобы не описывать процесс в общем виде (который вам, вероятно, никогда не понадобится), мы остановимся на системах счисления 2 8, 2 16.

Замечание. Вы будете гораздо быстрее осуществлять действия по переводу чисел в родственных системах счисления, если выучите наизусть таблицу соответствия цифр от О до 15 в двоичной, восьмеричной и шестнадцатеричной системах счисления (таблицу мы привели несколькими страницами ранее). Это существенно рэкономит вам время на экзамене.

При решении нижеследующих задач настоятельно рекомендуем этой таблицей не пользоваться — либо выучите ее наизусть, либо научитесь переводить числа «на лету». Если вы будете просто заглядывать в таблицу — не научитесь делать это сами и не сможете осуществлять перевод на экзамене.

2.25. Расставьте цифры    порядок выполнения действий при переводе из двоичной системы счисления в восьмеричную:


записать получившиеся цифры в том же порядке, в котором записаны группы разрядов сгруппировать разряды группами по З, справа налево двоичное число в каждой группе перевести в десятичную систему счисления

2.26. Переведите число 100011012 в восьмеричную систему счисления: 2 10

100011012 1012

2.28. Расставьте цифры — порядок выполнения действий при переводе из двоичной системы счисления в шестнадцатеричную:

записать получившиеся цифры в том же порядке, в котором записаны группы разрядов сгруппировать разряды группами по справа налево двоичное число в каждой группе перевести в десятичную систему счисления получившееся десятичное число перевести в 16-ю цифру

2.29. Переведите число 110101011012 в шестнадцатеричную систему счисления:

3210

              110101011012     11012  13

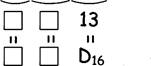
ния:

2.31. Расставьте цифры порядок выполнения действий при переводе из восьмеричной системы счисления в двоичную:

б выписать тройки двоичных разрядов друг за другом в том же порядке, в котором стоят цифры восьмеричного числа б каждую цифру восьмеричного числа перевести в двоичную систему счисления б если двоичное представление цифры состоит меньше чем из трех разрядов, дописать слева один или два нуля, чтобы всего получилось ровно три разряда

Пример.

5328 5 — 4 + 1 = 2 2 + 2 0 - 1012 З 2 1 = 2 1 + 2 0 — 112

1010110102

112 = 0112

2.32 Переведите число 7148 в двоичную систему счисления:

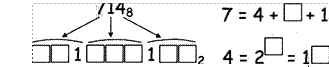              + 21 + 2 6612

1 12

2.33. Переведите числа 6038 и 3258 в двоичную систему счисления:

                        6038                   

2.34. Расставьте цифры — порядок выполнения действий при переводе из шестнадцатеричной системы счисления в двоичную:

б выписать четверки двоичных разрядов друг за другом в том же порядке, в котором стоят цифры шестнадцатеричного числа

если двоичное представление цифры состоит меньше чем из разрядов, дописать слева один или два нуля, чтобы всего получилось ровно        разряда каждую цифру шестнадцатеричного числа перевести в двоичную систему счисления

2.35. Переведите число D2716 в двоичную систему счисления: 02716

016 = 13 8 + 4 +1 = 2 3 + 2 2 + 2о = 11012

7=6+2 + 1 : 2 6 + 2 6 + 2

2.36. Переведите числа Е4З16 и АОС16 в двоичную систему счисления: Е4З16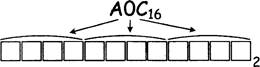      

2.37. Дано: а = D716, Ь = 3318. Какое из чисел с, записанных в двоичной системе, отвечает условию а < с < Ь?

            1) 11011001                    2) 11011100                    3) 11010111                    4) 11011000

Рекомендация. Так как все варианты ответов даны в двоичной системе счисления, имеет смысл перевести числа а и Ь в двоичную систему счисления, выбрать из них меньшее, прибавить к нему столбиком «1» и поискать результат среди вариантов ответа.

2.38. Дано: а = 2638, Ь       В516.

условию а < с < Ь?

            1) 10110010                     2)

2.39. Дано: а - Сб16, Ь - 3108.

1) 11000111

2)

2.40. дано: а = А416, Ь условию а < с < Ь?

2468.

1) 10100110

2)

2.41. Дано: а = 3418, Ь условию а < с < Ь?

Е316.

условию а < с < Ь?

            1) 11100000                    2)

Какое из чисел с,

10110101

Какое из чисел с,

11000101

Какое из чисел с,

10100111

Какое из чисел с,

11100001 записанных в двоичной системе, отвечает

3) 10110110                     4) 10110100

записанных в двоичной системе, отвечает

3) 11001001                       4) 11001000

записанных в двоичной системе, отвечает

3) 10100101                     4) 10100011

записанных в двоичной системе, отвечает

3) 11100010                     4) 11100100

2.42. Сколько единиц в двоичной записи числа 197?

2.43. Сколько единиц в двоичной записи числа 243?

2.44, Сколько значащих нулей в двоичной записи числа 124?

2.45. Сколько значащих нулей в двоичной записи числа 203?

Напоминание. для перевода дробных чисел в другую систему счисления нужно:

1.     Отдельно перевести целую часть по обычным правилам

2.     Дробную часть числа умножить на основание системы счисления

З. Из получившегося числа: целая часть (цифра) — записать ее как очередной разряд (дробный) результирующего числа и отбросить

4. Действия 2—3 повторять до тех пор, пока дробная часть не станет равна нулю или пока не будет достигнуто требуемое количество разрядов (точность)

Пример. Перевести число 7,625 в двоичную систему счисления.

Решение.

Переводим отдельно число 7: 7 = 4 + 2 + 1 = 2 2 + 2 1 + 20 1112.

Дробную часть числа (0,625) умножаем на 2. Получается 1,25.

Целую часть числа (1) дописываем после запятой в результирующее число.

Получается пока 111,12.

Отбрасываем целую часть. Остается 0,25. Умножаем ее на 2. Получается 0,5.

Целую часть числа (О) дописываем в результирующее число. Получается 111,102.

Отбрасываем целую часть (она в данном случае равна нулю, так что отбрасывать нечего).

Умножаем оставшееся на 2. Получается 1,0.

Целую часть числа (1) дописываем в результирующее число. Получается 111,1012.

Так как дробная часть числа получилась равна нулю, мы получили окончательный ответ: 7,62510 = 111,1012.

2.46. Сколько единиц в двоичной записи числа 67,5?

2.47. Сколько единиц в двоичной записи числа 23,375?

Ответ:

2.48. Сколько значащих нулей в двоичной записи числа 19,125?

Ответ:

2.49. Сколько значащих нулей в двоичной записи числа 37,875?

Ртдет:

2.50. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11.

Ответ:

Пример решения. Искомое число в четверичной системе счисления оканчивается на 4. Это значит, что оно имеет вид: Х 114, где Х — некоторое количество четверичных разрядов. По схеме перевода числа из четверичной системы счисления в десятичную получаем, что

                       = х • 4 2 + 1 • 4 1 + 1 = х . 16 + 4 + 1 - 16 . х + 5.

Это число должно быть не больше 25. Получаем неравенство: 16 • Х + 5 25. Это равносильно тому, что 16 • Х 20. При этом Х — целое неотрицательное число. Простым подбором получаем, что нас устраивают Х = О и Х = 1.

Значит, искомые числа: 16 • О + 5 и 16 • 1 + 5. То есть 5 и 21.

2.51. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 110.

Ответ:

2.52. Укажите через запятую в • порядке возрастания все десятичные числа, не превосходящие 25, запись которых в троичной системе счисления оканчивается на 21.

Ответ:

2.53. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 35, запись которых в системе счисления с основанием пять оканчивается на 13.

           Ответ:                                                  —l

2.54. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101.

Ответ:

2.55. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.

Ответ:

Пример решения. При переводе из десятичной в другую систему счисления нужно делить нацело с остатком исходное число на основание нужной системы счисления. При этом самый первый получающийся остаток это самый младший разряд результирующего числа. То есть именно на него результат будет оканчиваться. В данном случае остаток будет равен двум. Это означает, что исходное число 23 должно быть (по определению целочисленного деления с остатком) представлено в виде: 23 — пк + 2, где п и К — натуральные числа. Вычитая из обеих частей равенства 2, получаем 21 = пк. То есть достаточно найти все делители числа 21. При этом нужно не забыть, что остаток должен быть меньше делителя (основания системы счисления). Значит, нас устраивают все делители числа 21, которые больше двух. Это З, 7, 21.

2.56. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 27 оканчивается на З.

Ответ:

2.57. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 30 оканчивается на 8.

Ответ:

2.58. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4.

Ответ:

2.59.

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 29 оканчивается на З.

Ответ:

2.60. В системе счисления с некоторым основанием число 17 записывается в виде 101. Укажите это основание.

Ответ:

Пример решения. По правилу перевода числа в десятичную систему счисления из какойлибо другой (обозначим ее буквой Х):

По условию это число 17. Решаем уравнение Х + 1 17. Это равносильно Х2 = 16. Откуда Х = ±4. —4 отбрасываем, так как основание позиционной системы счисления должно быть больше 1. Ответ: 4.

2.61. В системе счисления с некоторым основанием число 19 записывается в виде 201. Укажите это основание.

Ответ:

2.62. В системе счисления с некоторым основанием число 30 записывается в виде 110. Укажите это основание.

Ответ:

2.63. В системе счисления с некоторым основанием число 21 записывается в виде 111. Укажите это основание.

Ответ:

2.64. В системе счисления с некоторым основанием число 57 записывается в виде 321. Укажите это основание.

I Ответ:

Напоминание. для правильного осуществления действий в системах счисления необходимы знания 1-го класса — как складывать и вычитать числа «столбиком». Вспомним это. Пусть необходимо сложить числа 2465 и 637. Обычные десятичные числа.

Если вы в лоб примените наработанные с детства методы в другой системе счисления— вы гарантированно ошибетесь. Например, с первого взгляда очевидно, что 5 + 7 = 12. Но вот 58 + 78 вовсе уже не равно 128. 58 + 78 = 148. Не поленитесь, аккуратно разберите следующий пример — как это нужно делать по действиям.

Сначала запишем оба исходных числа друг под другом, выровняв их по правомукраю (по младшему разряду):

2465

637

Начинаем с младшего разряда (самого правого). Сложим цифры. 5 + 7 = 12. Цифру «2» запишем в этом разряде, «1» (которая на самом деле 10) — это перенос в следующий разряд:

2465

л

В следующем разряде складываем 6 + З + 1 (из предыдущего разряда) = 10 Цифру «0» пишем в этом разряде, «1» — перенос в следующий разряд:

246 5

СКГЕДЫВаем 4 + б + 1 - — 11. «1» пишем, «1» — перенос в следующий разряд:

2 46 5

¯1T2

В самом левом (старшем) разряде стоит «2», плюс «1» перенесли из предыдущего разряда. Итого «З»:

2 4 6 5

Теперь попробуем сделать то же самое, но в восьмеричной системе счисления: 24658 + 6378

Запишем оба исходных числа друг под другом, выровняв их•по правому краю (по младшему разряду):

246 58

+ 6 З 78

Начинаем с младшего разряда (самого правого). Сложим цифры. 5 + 7 = 12. Но вот только это совсем теперь не значит, что «2» — пишем, а «1» — переносим. Потому что получившееся у нас 12 — это десятичное число. А нам нужно восьмеричное. Поэтому мы переводим 12 в восьмеричную систему счисления. В общем случае нужно бы, конечно, делить «уголком» и выписывать остатки от деления. Но при сложении двух чисел в любой системе счисления не может получиться перенос в следующий разряд больше, чем «1». Поэтому результат деления всегда будет давать «1» в качестве частного (если, конечно, случился перенос). А это значит, что вместо деления «уголком» достаточно просто вычесть из получившейся суммы основание системы счисления. В данном случае 12 —8 = 4. То есть «4» пишем, «1» — переносим:

24 6 58

                                                                                                                           8              

л

В следующем разряде стадываем 6 + З + 1 (из предыдущего разряда) = 10. Это 8. Значит, перенос есть. Вычитаем 8: 10 — 8 = 2.

Цифру «2» пишем в этом разряде, «1» — перенос в следующий разряд:

24 6 58

Складываем 4 + 6 + 1 = 11. Перенос есть. Вычитаем 8. «З» пишем, «1» — перенос в следующий разряд:

2 4 6 58

В самом левом (старшем) разряде стоит «2», плюс «1» перенесли из предыдущего разряда. Итого «З». Переноса нет:

2 4 6 58

2.65.   Чему равна сумма чисел 438 и 568 (в восьмеричной системе счисления)?

2.66.   Чему равна сумма чисел 1101101102 и 11101112 (в двоичной системе счисления)?

2.67.   Чему равна сумма чисел 1324 и 2334 (в четверичной системе счисления)?

Замечание. При действиях в шестнадцатеричной системе счисления нужно помнить таюке о том, что если в разряд нужно записать число, например 13, — это не значит, что «З» пишем, а «1» — переносим. Это значит, что в этом месте нужно написать шестнадцатеричную цифру «D».

Пример. Найти сумму чисел DF516 и В716 в шестнадцатеричной системе счисления.

Решение.

В младшем разряде: 5 + 7 — 12. Это не значит, что «2» — пишем, а «1» — переносим. Так как 12 16, то переноса нет. Нужно просто вспомнить, что 12 = С16:

D Р 516

В следующем разряде: F + В. Вспоминаем, что F16 — 15, а = 11 То есть 15 + 11 = 26. 26 2 16. Перенос есть.

Вычитаем 16 из 26: 26 — 16 = 10.

Вспоминаем, что 10 = Аш. «А» — пишем, «1» — переносим:

DF 516

                                                                                        7

16

В старшем разряде было «D» . Плюс «1» перенесли. Значит, будет следующая шестнадцатеричная цифра (буква «Е»). Получаем:

DF 516

2.68. Чему равна сумма чисел CD16 и АЕ16 (в шестнадцатеричной системе счисления)?

2.69. Чему равна сумма чисел 438 и 5616?

            1) 1218                              2) 1718                             3) 6916                               4) 10000012

Рекомендация. Так как числа в условии и в вариантах ответа даны в разных системах счисления (причем родственных), имеет смысл сложение осуществлять в той системе счисления, из которой проще будет потом переводить в две другие. То есть в двоичной системе счисления. Если сумма двух исходных чисел в двоичной системе счисления не совпадет с двоичным вариантом, ее нужно будет перевести (группированием разрядов) в восьмеричную систему счиапения и сравнить с другими вариантами. Если и здесь не будет совпадений — перевести сумму в шестнадцатеричную систему счисления и сравнить с имеющимся вариантом.

2.70. Чему равна сумма чисел 528 и 7416?

            1) 1268                             2) 5Е16                                                                        3)4) 2368

2.71. Чему равна сумма чисел 618 и 4516?

            1) 7516                             2) 11101102                    3) 1658                               4) 1778

2.72. Чему равна сумма чисел 708 и 2316?

            1) 1738                             2) 7В16                              3) 1338                             4)

2.73. Чему равна сумма чисел 238 и 6716?

                                               1) 7А163) 1708                                                               4) 3816

2.74.


Вычислите сумму чисел х и у, при х 1D16, у 728. Ответ приведите в двоичной системе счисления.

Рекомендация. Если нужно найти сумму чисел, представленных в разных системах счисления, то нужно привести их в одну систему счисления. Если нужно сложить число в шестнадцатеричной и в восьмеричной системах счисления, проще всего перевести оба числа в двоичную систему счисления.

2.75. Вычислите сумму чисел х и у при х = Аб16, у = 758. Ответ приведите в двоичной системе счисления.

2.76. Чему равна сумма чисел 4D16 и 568? Ответ приведите в двоичной системе счисления.

Напоминание. После сложения перейдем к вычитанию. Вспомним, как вычесть из 2007 число 29.

Запишем меньшее под большим, выровняв по правой цифре.

Начинаем с младшего (правого) разряда. Пытаемся вычесть из семи девять. Не получается (9 > 7). Значит, нужно занять в предыдущем разряде. Но там стоит ноль. Значит, нужно занять в еще более предыдущем разряде. Но там тоже ноль. Значит, занимаем в еще более предыдущем:

2007

                                                                      29    

Из старшего разряда заняли «1». Значит, там осталось еще «1», в следующий разряд «свалилось» 10. Но из него заняли «1» (осталось 9). В следующий разряд тоже «свалилось» 10, заняли «1», осталось 9. В младший разряд «свалилось» 10. Плюс там уже есть 7. Итого 10 + 7 = 17. Из этих 17 теперь вычитаем 9: 17 — 9 = 8. Это «8» пишем в младший разряд:

-2007

29

Переходим к следующему разряду. Там над «0» стоит точка. Это напоминание, что мы из этого разряда занимали. Значит, сверху осталось «9» (самая старшая цифра нашей системы счисления), вычитаем из нее «2»: 9 — 2 = 7. Пишем это «7» в данный разряд:

5007

29

В следующем разряде вычитать уже ничего не нужно. Сверху стоит «0» с точкой над ним. Значит, это «9». Списываем это «9» вниз, в результат:

 2007

29

В старшем разряде «2», над которой стоит точка. Значит, из этих «2» осталось «1». Снизу вычитать рке ничего не надо, списываем эту «1» вниз, в результат:

-2007

29

Рассмотрим то же действие, но теперь в шестнадцатеричной системе счисления:

200716 - 2916

Запишем меньшее под большим, выровняв по правой цифре.

Начинаем с младшего (правого) разряда. Пытаемся вычесть из семи девять. Не получается (9 > 7). Значит, нужно занять в предыдущем разряде. Но там стоит ноль. Значит, нужно занять в еще 60лее предыдущем разряде. Но там тоже ноль. Значит, занимаем в еще более предыдущем. Пока все как в десятичной системе счисления:

_>00716

2 916

Из старшего разряда заняли «1». Значит, там осталось еще «1», в следующий разряд «свалилось»... нет, не 10, как раньше. Ведь у нас не десятичная система счисления и вес каждого более старшего разряда не в 10 раз больше младшего, а в 16! То есть в следующий разряд «свалилось» 16. Но из него заняли «1» (осталось 15). В следующий разряд тоже «свалилось» 16, заняли «1», осталось 15. В младший разряд «свалилось» 16. Плюс там уже есть 7. Итого 16 + 7 = 23. Из этих 23 теперь вычитаем 9: 23 — 9 = 14. Но это «14» мы не пишем в младший разряд. Потому что у нас шестнадцатеричная система счисления и 14 — это должна быть одна цифра. То есть «Е»:

200716

29

Переходим к следующему разряду. Там над «О» стоит точка. Это напоминание, что мы из этого разряда занимали. Значит, сверху осталось 15, вычитаем из нее «2»: 15 — 2 = 13. Это «D». Пишем это «D» в данный разряд:

200 716

2 9

16

В следующем разряде вычитать уже ничего не нужно. Сверху стоит «О» с точкой над ним. Значит, это «F» (самая старшая цифра в шестнадцатеричной системе счисления). Списываем это «F»

вниз, в результат:

20 0 716

2 9

16

В старшем разряде «2», над которой стоит точка. Значит, из этих «2» осталось «1 Снизу вычитать уже ничего не надо, списываем эту «1 » вниз, в результат:

-20 0 716 2 9

2.77. Чему равно Аб16—758?

1) 318

2.78. Чему равно 6816—558?               

2) 1518

3) 3116

4) 15116

1) 738

2) 538

3) 7316

4) 5316

2.79. Число 48 в системе счисления с некоторым основанием записывается как 60. Укажите это основание.

Рекомендация. Обозначим искомое основание как N. Переведем число 60N в десятичную систему счисления. Получим: 6*N1 +0*N0 = 6N. Известно, что это равно 48. Решаем уравнение 6N = 48

и находим N.

2.80. Число 36 в системе счисления с некоторым основанием записывается как 40. Укажите это основание.

2.81. Число 72 в системе счисления с некоторым основанием записывается как 40. Укажите это основание.

2.82. Комплексное задание в системах счисления.

1)                Получить исходное число: 230 + N (выберите N от 1 до 25).

2)                Перевести число (столбиком) в двоичную, троичную, пятеричную ССч. З) К полученному двоичному числу прибавить 10112 (столбиком).

4)     Результат перевести в восьмеричную и шестнадцатеричную ССч (объединением разрядов).

5)     К полученному восьмеричному числу прибавить (столбиком) 378.

6)     Результат перевести в десятичную ССч.

7)     Из полученного шестнадцатеричного числа отнять (столбиком) 1F16 8) Результат перевести в десятичную ССч.

9) К полученному троичному числу прибавить (столбиком) 2123. 10) Из полученного пятеричного числа отнять (столбиком) 345

Схема выполнения задания:

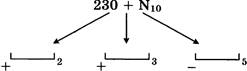
                           10112                2123                 345

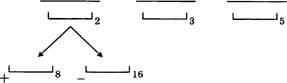
                      378             1F16

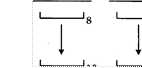
                                  10                      10

2.83. [1][2]Сколько единиц содержится в двоичной записи значения выражения: 4 2013 + [3]2010

Пример решения. Двоичная запись выражения 2 п , где п целое положительное число, в двоичной системе счисления будет иметь вид 100...00 . Запишем в двоичном виде первое и второе слагаемые 42013 4026 - lOO...002, [4]2011 100...002. Мысленно скла-

4026 2010 дывая эти числа поразрядно справа налево «в столбик» получаем lOO...00100...00 2. Да-

2015    2010 лее из получившегося числа вычитаем единицу, учитывая что 100...00 2-1     01 1...1 12,

п

(ведущий ноль оставлен для наглядности). Получаем 100...0001 1...1 12. В итоге имеем

                                                                                                                                                                                                                                          2015                2010

2010 единиц справа и одну слева. Ответ: 2011.

2.84. Сколько единиц содержится в двоичной записи значения выражения: 4 2013 + [5]2010 - 15?

Пример решения. Перепишем выражение в виде 4 2013 + 22010 16 + 1 = 2 4026 + 22010                                                                                                                                24 + 1.

В предыдущем примере показано, что 2 4026 + 22010          100...00100...002. Вычитая в столбик

                                                                                                                                                                                                                        20 Ё 5              2010

4100002, получаем 100...0001 1...1 10...02. Четыре самых правых нуля остались на месте,

2.89. Сколько единиц содержится в двоичной записи восьмеричного числа 17318

Рекомендации по решению. Переводим число в двоичную систему счисления. Для этого каждую цифру заменяем на соответствующий ей двоичный З-разрядный код (перевод из 8-ричной системы в 2-ичную, 8 2 3 ). Для этого либо нужно помнить таблицу соответствия, либо быстро составить ее на черновике.

Подсчитываем в получившейся последовательности число единиц.

В данном примере 1      001, 7      111, з      011, 1      001. Число единиц — 7.

Если исходное число дано в 16-теричной системе счисления, нужно заменять каждую 16-теричную цифру на 4-разрядный двоичный код (16 = 2 4 ).

Быстрый способ построения таблицы соответствии:

Понимаем, что в таблице будет 8 строк и 1 + З столбца (один столбец для нумерации строк). Начинаем заполнять таблицу по столбцам.

Сначала составим столбец, нумерующий все строки. Нумеруем от нуля. Так как всего 8 строк, последняя строка будет иметь номер 7. Теперь в следующем столбце выписываем половину нулей, затем вторую половину единиц (всего 8 строк, половина = 4):

В следующем столбце нули и единицы будут чередоваться вдвое чаще. То есть, 2 нуля, 2 единицы, 2 нуля, 2 единицы: о: оо 1: оо 2: 01 з: 01 4: 10

5: 10

6: 11

7: 11

В следующем столбце чередование будет еще вдвое чаще. То есть, 0/1/0/1/... о: 000 1: 001 2: 010 з: 011 4: 100

5: 101

6: 110

7: 111

Если нужно составить таблицу для 16-теричной системы, делаем так же, но не забываем, что номера столбцов будут от О до 9, потом А, В, С, D, Е, Р. Строк будет 16. Поэтому в первом столбце будет 8 нулей и 8 единиц. Во втором по 4 нуля/4 единицы дважды. В третьем — по 2 нуля/2 единицы четырежды. В последнем столбце нули и единицы будут через один.

2.90. Сколько единиц содержится в двоичной записи восьмеричного числа 24568

2.91. Сколько единиц содержится в двоичной записи шестнадцатеричного числа ЗЕА216

2.92. Сколько единиц содержится в двоичной записи шестнадцатеричного числа D7BF16

2.93. Сколько единиц содержится в двоичной записи значения выражения: 4 16 + 2 36

Пример решения. Переведем каждое слагаемое в степень двойки.

Получаем 2 32 + 2 36   2 4 . Запишем слагаемые в порядке убывания степеней:

2 36 + 2 32

Исследуем, что за двоичное число получается при вычислении 2 Х—2 У . Рассмотрим на примере 2 8-2 5 . 2 8 = 1000000002, 2 5 - 1000002.

_1000000002

1000002

111000002 то есть, 2 8 -2 5         это З единицы и 5 нулей. Нетрудно сделать вывод, что 2 х  это (х — у) единиц и (у) нулей. Значит, в нашем примере 2 36     2 — это 32 единицы и еще 4 нуля. А при добавлении к этому еще 2 36 в начале двоичной записи добавится еще одна единица. Значит, ответ — 33 единицы.

2.94. Значение арифметического выражения: 9 200 + 3 100 2 — записали в системе счисления с основанием З. Сколько цифр «2» содержится в этой записи?

Пример решения. Переведем каждое слагаемое в степень тройки. То же сделаем с числом 2 (= З — 1 = 3 1 — 3 0 ).

Получаем 3 400 + 3 100 - (3 1 - 3 0 ) = 3 400 + 3 100                                                         3 1 + 30 .

Исследуем, что за троичное число получается при вычислении З Х—З У . Рассмотрим на примере 3 8 -3 5 . 3 8 - 1000000003, 3 5 1000003.

-1000000003

1000003

222000003

То есть, З — это З двойки и 5 нулей. Нетрудно сделать вывод, что зх — З У — это (х — у) двоек и (у) нулей. Значит, в нашем примере 3 100 — это 99 двоек и еще О. А при добавлении к этому 3 400 в начале троичной .записи добавится еще одна единица. Добавление 3 0 повлияет только на нулевую позицию результата. Там стоит О. Значит, в ответе на нулевой позиции будет стоять 1 и это не повлияет .на остальные разряды. Значит, ответ — 99 двоек.

2.95.

70

2.96. Значение арифметического выраэкения: 9 30 + З 25 — записали в системе счисления с основанием З. Сколько цифр «2» содержится в этой записи?

2.97. Значение арифметического выражения: 25 30 + 4 • 5 70 21 — записали в системе счисления с основанием 5. Сколько цифр «4» содержится в этой записи?

З. КОДИРОВАНИЕ ИНФОРМАЦИИ

Основные понятия

Для удобства представления информации в компьютере все возможные виды информации переводятся в числовую форму, и эти числа хранятся в компьютере в двоичном виде.

Для кодирования текстовой информации используются специальные таблицы, в которых каждому символу (в т.ч. каждой букве) поставлен в соответствие некоторый номер. Так как эти номера хранятся в двоичном виде, принято говорить, что каждому символу соответствует свой двоичный код. Длина этих двоичных кодов одинакова для всех символов таблицы.

Основной (традиционной) таблицей кодирования символов является таблица ASCII (американский стандартный код обмена информацией, читается «АСКИ»). В ней для хранения каждого символа выделено 8 бит (1 байт). Таким образом, общее количество различных символов, которое кодируется таблицей ASCII, равно 28 - 256.

Для кодирования русских букв, в зависимости от операционной системы, используется одна из разновидностей таблицы ASCII (так называемая кодовая странна): КОИ-8, Windows-1251, IS0, DOS, МАС.

Из-за ограниченности количества различных символов в таблице ASCII на смену ей придумана кодовая таблица Unicode (Юникод). В ней для хранения каждого символа используется 16 бит (2 байта). Таким образом, общее количество различных символов, которое кодируется таблицей Unicode, равно 216 - 65 536.

Для кодирования информации о цвете используется таблица цветов. Количество цветов N, которое может быть закодировано при помощи i бит, вычисляется по формуле:

Для кодирования полноцветных изображений используют цветовые модели (способ представления информации о цвете через несколько характеристик цвета). Одна из основных цветовых моделей — RGB. Она хранит информацию о цвете в виде яркости трех базовых цветов — красного (red), зеленого (green) и синего (blue), каждая из которых может принимать значения от О до 255. Эти три цвета «складываются» при восприятии их человеком, и он воспринимает их как некоторый оттенок цвета. Эта цветовая модель (RGB) называется аддитивной, потому что яркости базовых цветов в ней складываются (add). Чем больше суммарная яркость, тем светлее общий оттенок цвета и наоборот.

То есть, если все три яркости равны нулю, получается черный цвет, если 255, то белый. Если все три яркости одинаковы и лежат между О и 255, получается оттенок серого цвета. Если в коде цвета присутствует только одна яркость из трех, получается оттенок этого цвета.

Для кодирования растровых изображений цвет каждого пикселя изображения записывается своим кодом (одинаковой длины для всех пикселей изображения). Таким образом, общий объем памяти, необходимый для хранения неупакованного растрового изображения можно вычислить, умножив количество пикселей на длину кода цвета одного пикселя. Число пикселей в растровом изображении ширина, умноженная на высоту. Так как длина кода цвета обычно записана в битах, а объем памяти принято считать в байтах, получившуюся величину нужно поделить на 8. Получаем формулу:

где Н и W — высота и ширина изображения в пикселях,

С — число бит, используемое для хранения кода цвета одного пикселя, — объем памяти для хранения этого изображения в байтах.

Кодирование звука. Нужно понимать, что с точки зрения компьютера звук — это колеблющаяся с определенной частотой мембрана (при воспроизведении звука колебания мембраны создают колебания воздуха (звуковую волну), которую слышит ухо). Для кодирования звука записывают отклонение мембраны от нулевого положения определенное количество раз в секунду. Это количество раз в секунду называют частотой дискретизации. Значение отклонения мембраны кодируют в двоичной системе счисления. Это может быть осуществлено с разной точностью. Значение максимального отклонения разбивают на какое-то количество делений (квантуют). Это количество делений называется количеством уровней квантования. Так как отклонение записывают в двоичной системе счисления, количество уровней квантования выбирают равным степени двойки. Соответственно, количество уровней квантования связано с количеством бит, требуемым для кодирования, все тем же соотношением:

Здесь N — количество уровней квантования, i — количество бит, которым кодируется каждое отклонение мембраны. Общая формула вычисления объема звукового файла:

vx t x i / 8, где Ch — количество каналов (обычно 1 (моно), 2 (стерео) или 4 (квадро)), v — частота дискретизации в Герцах, t — время звучания/звукозаписи в секундах, число бит разрешения (делим на 8, чтобы получить в ответе байты),

V — объем памяти для хранения этого звукового фрагмента в байтах.

Практическая часть

3.1. Выберите правильный ответ. В каком виде хранится вся информация в компьютере? (Обведите букву, соответствующую правильному утверждению.)

а) Для каждого вида информации придуман свой тип файла.

б) В двоичном (для всех видов информации придуманы свои двоичные коды).

в) Числа хранятся как числа, буквы — как буквы, изображения — как точки.

3.2. Укажите одно или несколько правильных утверждений. Буквы, соответствующие правильным утверждениям, обведите, остальные — зачеркните.

Относительно кодирования текстовой (символьной) информации можно сказать следующее:

а) для каждого символа выделен свой код. Эти коды хранятся в виде двоичных чисел одинаковой длины;

б) часто для кодирования символов используется таблица, состоящая из 256 различных символов. Она называется ASCII. Для хранения каждого символа выделено 8 бит (1 байт);

в) при кодировании русских букв в коде ASCII используется один из пяти различных способов: КОИ-8, Windows-1251, ISO, DOS, МАС. Обычно способ кодирования выбирается в зависимости от используемой операционной системы;

г) часто для кодирования символов используется таблица, состоящая из 65 536 различных символов. Она называется Unicode. Для хранения каждого символа выделено 16 бит (2 байта);

д) таблица Unicode была придумана для универсальности хранения символов различ ных национальных алфавитов. Она должна была заменить таблицу ASCII. Однако удвоение необходимого объема памяти и консервативность пользователей не позволяет ей пока полностью заменить таблицу ASCII.

3.3. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 480 бит. Какова длина сообщения в символах?

Рекомендация. Обозначьте за х количество символов в сообщении. Составьте уравнение: количество бит, которое было первоначально, минус количество бит после перекодировки равно 480. Найдите х.

3.4. Считая, что каждый символ кодируется двумя байтами, оцените информационный объем (в битах) следующего предложения в кодировке Unicode: один пуд около 16,4 килограмма.

3.5. В кодировке Unicode на каждый символ отводится два байта. Определите информационный объем (в битах) слова из двадцати четырех символов в этой кодировке.

3.6. Сообщение из 50 символов было записано в 8-битной кодировке Windows-1251. После вставки в текстовый редактор сообщение было перекодировано в 16-битный код Unicode. На какое количество информации увеличилось количество памяти, занимаемое сообщением?

            1) 100 бит                       2) 50 бит                          З) 400 байт                      4) 50 байт

Напоминание. Для записи текстовой информации не обязательно использовать стандартные 8-битные и 16-битные кодовые таблицы. Если количество различных символов в сообщении мало, можно использовать особые, короткие, коды для записи каждого символа (но в этом случае источник сообщения и приемник сообщения должны неким образом договориться об одинаковом способе кодирования).

Последовательности нулей и единиц, которыми кодируются символы сообщения, называются кодовыми словами.

Если вероятность появления каждого символа сообщения одинакова, то символы кодируют кодовыми словами одинаковой длины.

3.7. букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится:

                                                    2) 411                                 3) BACD                          4) 1023

Рекомендация. Составьте таблицу кодовых слов (выпишите кодовое слово для каждой буквы). Закодируйте данную последовательность символов, выписав коды букв в том же порядке, что и буквы исходного сообщения, согласно этой таблице. Вспомнив процедуру перевода из двоичной системы счисления в шестнадцатеричную, сгруппируйте получившиеся двоичные цифры по 4 и вместо каждой группы напишите соответствующую шестнадцатеричную цифру.

3.8. Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ВАБВГАБГ и записать результат шестнадцатеричным  кодом, то получится:

             1) совс                            2) 20123013                    3) A8D5                           4) 86C7

3.9. Сообщение состоит из символов М, А, Ы, Л, Р, У, точек и пробелов. Каким минимальным количеством байт можно закодировать сообщение, если оно состоит из 1000 таких символов?

Напоминание. Если вероятность появления каждого символа сообщения не одинакова, то символы кодируют кодовыми словами разной длины. В этом случае нужно использовать такой способ кодирования, чтобы принятое сообщение можно было однозначным образом декодировать. Самый распространенный способ — использование префиксного кода (когда никакое кодовое слово не является началом никакого другого кодового слова).

3.10. Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

 

в

 

 

 

000

01

100

10

011

Определить, какой набор букв закодирован двоичной строкой 0110100011000

            1) ЕВСЕА                         2) BDDEA                        3) BDCRA                        4) ЕВАЕА

Рекомендация. Выпишите передаваемое сообщение и начните разделять его на кодовые слова, подбирая их по таблице. Обратите внимание: код в данном случае постфиксный. Поэтому сообщение нужно однозначно декодировать справа налево.

3.11. Для 5 букв русского алфавита заданы их двоичные коды (для некоторых букв из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

в

 

 

 

 

000

11

01

001

10

Из четырех полученных сообщений в этой кодировке только одно прошло без ошибки и может быть корректно декодировано. Найдите его:

1)     110100000100110011  3) 110100001001100111

2)     111010000010010011  4) 110110000100110010

3.12. Через канал связи передается сообщение, состоящее только из символов А, Б, В, Г и Д. Каждый символ при этом кодируется своим собственным кодом: А—11, Б— 100, В—ОО, Г—О1. Каким самым коротким кодовым словом нужно закодировать символ Д, чтобы код удовлетворял свойству однозначного декодирования?

            1) 1000                             2) 10                                 3) 101

Рекомендация. Чтобы код удовлетворял свойству однозначного декодирования, он должен быть префиксным. То есть никакое кодовое слово не должно быть началом никакого другого кодового слова. Исследуем имеющиеся кодовые слова и построим дерево декодирования. В каждом узле дерева декодирования принимается решение, в какую сторону «повернуть» — направо или налево. Будем рисовать начиная от некоего начального (корневого) узла, ветки. для «1» будем рисовать ветку направо, для «0»— налево:

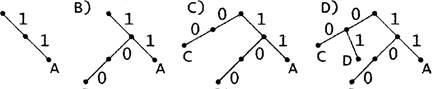
                                             В                         в                         в

Начинаем добавлять в дерево первую букву (А). Ее код — две единицы, рисуем две ветки вправо. Потом добавляем вторую букву (В). Ее код — 100, одна ветка вправо (уже есть), от этого узла две ветки влево. Добавляем третью букву (С). Ее код — два нуля, две ветки влево. Добавляем четвертую букву (0). Ее код — 01, одна ветка влево (уже есть), одна ветка вправо. для всех известных кодов букв построили дерево декодирования. Теперь ищем в получившемся дереве, у какого узла нет второй ветки. Это узел «10». У него отсутствует ветка вправо. То есть, ветка «1». Получается, что у недостающей буквы самое короткое кодовое слово должно быть 101.

3.13. Через канал связи передается сообщение, состоящее только из символов А, Б, В, Г и Д. Каждый символ при этом кодируется своим собственным кодом: А—111, Б—О, В— 101, Г— 110. Каким самым коротким кодовым словом нужно закодировать символ Д, чтобы код удовлетворял свойству однозначного декодирования?

            1) 1001                                                                       3) 10                                 4) 100

3.14. Через канал связи передается сообщение, состоящее только из символов А, Б, В, Г и Д. Каждый символ при этом кодируется своим собственным кодом: А—11, Б—1О, В—О11, Г—О1О. Каким самым коротким кодовым словом нужно закодировать символ Д, чтобы код удовлетворял свойству однозначного декодирования?

                                                                                                3) 001                               4) 111

3.15. Через канал связи передается сообщение, состоящее только из символов А, Б, В, Г и Д. Каждый символ при этом кодируется своим собственным кодом: А—11О, Б—111, В— 100, Г—1О1. Каким самым коротким кодовым словом нужно закодировать символ Д, чтобы код удовлетворял свойству однозначного декодирования?

                                                                                                 3) 000                               4) 0000

Напоминание.                                       цвета используются цветовые модели.

Цветовая модель — способ сопоставления каждому используемому в модели цвету своего кодового слова.

Считается, что человеческий глаз способен различать 16 миллионов опенков цвета.

Так как составить таблицу всех 16 миллионов цветов и назвать каждый представляется затруднительным и малоэффективным способом, придумали правила, по которым значение цвета хранится как числовое значение его определенных характеристик.

Самый распространенный такой способ — представлять цвет как интенсивность свечения трех базовых цветов, из которых можно составить любой из 16 миллионов цветов. (Вообще говоря, правильнее сказать «почти любой». Но это слишком сложно, чтобы изучать в курсе школьной информатики). Такая цветовая модель называется RGB. В ней для указания цвета используются яркости (интенсивности свечения) красного (Red), зеленого (@reen) и синего (Дие) цветов. Каждая яркость может принимать значение от нуля (отсутствие свечения) до 255 (максимальное свечение). То есть всего по 256 возможных состояний.

вы, вероятно, понимаете, что количество цветов (равновероятных событий) и количество бит для хранения кода цвета (количество информации) связано соотношением

                                                                  2число бит = число цветов                                                        (3.1)

То есть для хранения интенсивности каждого базового цвета требуется 8 бит (2число бит = 256) или 1 байт. Значит, для хранения кода всего цвета требуется З • 8 = 24 бита или З байта. Заметим, что 224 как раз примерно равно 16 миллионам.

В цветовой модели RGB работают все современные мониторы и телевизоры. В этой же цветовой модели представляется цвет в различных программах. В частности, для указания цвета фона (в файле формата HTML) тоже используется цветовая модель RGB. для этого используется атрибут bgc010r тега  который записывается в виде #RRGGBB. Здесь RR — шестнадцатеричный код красной цветовой компоненты, GG — шестнадцатеричный код зеленой цветовой компоненты, ВВ — шестнадцатеричный код синей цветовой компоненты. Напоминаем, чем больше значение компоненты, тем больше интенсивность свечения соответствующего базового цвета. 00 — отсутствие свечения, FF — максимальное свечение (FF16 = 25510). Рассмотрим коды основных цветов, получающиеся из этих соображений:

#FFOOOO красный (красная составляющая максимальная, остальные равны нулю)

#OOOOOO черный (ни одна компонента не светится)

#FFFFFF белый (все составляющие максимальны и одинаковы, наиболее яркий цвет)

#404040 темно-серый (все составляющие одинаковы, значит, ни один из базовых цветов не выделяется из остальных (серый); число 4016 меньше, чем среднее значение яркости (8016), значит, это темный цвет

3.16. Установите соответствие между кодами цвета и их названиями (соедините линиями).

 

Код цвета

Название цвета

а)

#OOOOFF

1) средней яркости серый

6)

#OOFFOO

2) почти черный

в)

#808080

З) темно-синий

г)

#сососо

4) светло-серый

 д)

#010101

5) синий

е)

#000080

6) зеленый

Напоминание. Принципы смешения базовых цветов отличаются от тех принципов смешения красок, которые привиты каждому ребенку на уроках рисования. Если смешать красный и синий, то все же получится фиолетовый. А вот если смешать желтый и синий, то получится вовсе не зеленый, а белый цвет. (Различие связано с тем, что на рисовании смешиваются краски, а не самосветящиеся источники. для красок физический принцип получения цвета и другая цветовая модель — СМУК.) Чтобы попытаться понять эти принципы, рекомендуем запомнить схему смешения цветов:

Красный

ЖелтыйМалиновый

(фиолетовый)

ЗеленыйСиний

Небесно-голубой

Если смешиваются две базовые компоненты с равными яркостями, получится цвет, расположенный на схеме между ними, светлость/темность которого зависит от этих яркостей (чем ярче, тем светлее, чем меньше яркость, тем темнее).

Если нужно получить, например, светло-красный — очевидно, что нужно увеличить общую яркость по сравнению с красным цветом. Увеличивать яркость красной компоненты (#FFOOOO) уже некуда (она максимальна). Если увеличить одну из оставшихся компонент — в цвете будет присутствовать этот опенок. Значит, нужно увеличить яркости обеих оставшихся компонент — #FF8080.

3.17. Установите соответствие между кодами цвета и их названиями (соедините линиями)

                  Код цвета                                                                  Название цвета

а) #FFFFOO  1) темно-малиновый 6) #FFFF80           2) малиновый

             в) #40FF40                                                                З) желтый

             г) #FFOOFF                                                                4) светло-желтый

             д) #800080                                                                5) светло-зеленый

Если две компоненты смешиваются в разных пропорциях, получится опенок между базовым цветом и тем, КОТОРЫЙ указан между ними. Самый понятный пример — оранжевый цвет. Все понимают, что это нечто среднее между желтым и красным.

Желтый — #FFFFOO, красный — #FFOOOO. Можно просто найти среднее арифметическое по каждой компоненте в отдельности: R = (FF + FF) 2 = FF, G = (FF + 00) 2 80, В = (0 + 0) 2 = О. То есть оранжевый — #FF8000.

3.18. Для кодирования цвета фона страницы Интернет используется атрибут bgcolor =”#ХХХХХХ”, где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной Какой цвет будет у страницы, заданной тэгом <body bgcolor

             1) Белый                          2) Зеленый                      З) Красный                     4) Синий

3.19. Для кодирования цвета фона страницы Интернет используется атрибут bgcolor ="#ХХХХХХ”, где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной  Какой цвет будет у страницы, заданной тэгом <body bgcolor =”#404000">?

            1) Серый                         2) Фиолетовый              З) Темно-красный         4) Коричневый

3.20. цвета фона страницы Интернет используется атрибут bgcolor =”#ХХХХХХ”, где в кавычках задаются шестнадцатеричные значения интенсивности цветовых компонент в 24-битной Какой цвет будет у страницы, заданной тэгом <body bgcolor

            1) Серый                         2) Фиолетовый              З) Темно-красный         4) Коричневый

Напоминание. Растровое изображение состоит из прямоугольного набора точек (пикселей), для каждой из которых хранится код цвета этой точки.

Формула соотношения количества бит, выделенных для хранения кода цвета и количества цветов, которые могут быть таким образом закодированы, мы уже приводили:

число бит = число цветов

3.21. Какой минимальный объем памяти (в битах) необходим для хранения одной точки изображения, в котором 16 различных цветов?

3.22. Какой минимальный объем памяти (в битах) необходим для хранения одной точки изображения, в котором 2 различных цвета?

3.23. Какой минимальный объем памяти (в битах) необходим для хранения одной точки изображения, в котором 256 различных цветов?

3.24. Какой минимальный объем памяти (в битах) необходим для хранения одной точки изображения, в котором 32 различных цвета?

3.25. Какой минимальный объем памяти (в битах) необходим для хранения одной точки изображения, в котором 128 различных цветов?

3.26. Какое наибольшее количество различных цветов можно закодировать, используя 4 бита?

3.27. Какое наибольшее количество различных цветов можно закодировать, используя З бита?

3.28. Какое наибольшее количество различных цветов можно закодировать, используя 1 бит?

3.29. Какое наибольшее количество различных цветов можно закодировать, используя 8 бит?

3.30. Какое наибольшее количество различных цветов можно закодировать, используя 16 бит?

Напоминание. В растровом изображении (неупакованном) каждый пиксель кодируется одинаковым количеством бит. Изображение при этом состоит из прямоугольной таблицы пикселей (таблицы). Значит, чтобы посчитать количество бит, необходимых для хранения растрового изображения, нужно количество пикселей умножить на количество бит в одном пикселе.

Количество пикселей в изображении можно получить, перемножив количество пикселей по ширине и по высоте. При этом размер необходимой памяти принято измерять не в битах, а в байтах. Чтобы осуществить перевод в байты, нужно результат поделить на 8.

Итоговая формула для расчета количества памяти которое необходимо выделить для хранения неупакованного растрового изображения размером Н х W пикселей, в котором для хранения одного пикселя требуется С бит:

                                            v=Hx wx C/8                                            (3.2)

3.31. Для хранения растрового изображения разщером 32 х 32 пикселя потребовалось 512 байт памяти. Каково максимально возможное число цветов в палитре изображения?

            1) 256                                                                         3) 16

Рекомендация. для формулы (3.2) в данной задаче имеются Н = 32, W= 32,                512. Найдем С:

512 = 32 х 32 х с / 8

По формуле (3.1) получаем, что число цветов равно 2        16.

3.32. Какой объем информации (в килобайтах) занимает неупакованное полноцветное (2 24 цветов) растровое изображение размером 1024 х 512 пикселей?

Ответ:

3.33. Какой объем информации (в килобайтах) занимает неупакованное растровое изображение размером 256 х 512 пикселей в цветовом режиме HighColor (2 16 цветов)?

Ответ:

3.34. Какой объем информации (в килобайтах) занимает неупакованное растровое изображение размером 160 х 2048 пикселей в цветовом режиме GrayScale (256 оттенков серого)?

Ответ:

3.35. Рассчитайте объем (в килобайтах) 4-цветного неупакованного растрового изображения размером 256 х 128 пикселей.

Ответ:

3.36. Рассчитайте объем (в килобайтах) 8-цветного неупакованного растрового изображения размером 256 х 512 пикселей.

 

Ответа

3.37. Какова ширина (в пикселях) прямоугольного 64-цветного неупакованного растрового изображения, занимающего на диске 1,5 мегабайта, если его высота вдвое меньше ширины?

Ответ:

3.38. Какова ширина (в пикселях) прямоугольного 16-цветного неупакованного растрового изображения, занимающего на диске 1 мегабайт, если его высота вдвое больше ширины?

Ответ:

3.39. Скольких различных цветов могут быть пиксели неупакованного растрового изображения, имеющего размер 1024 х 256 пикселей и занимающего на диске 160 килобайт?

3.40. Скольких различных цветов могут быть пиксели неупакованного растрового изображения, имеющего размер 128 х 512 пикселей и занимающего на диске 24 килобайта?

3.41. Скольких различных цветов могут быть пиксели неупакованного растрового изображения, имеющего размер 128 х 4096 пикселей и занимающего на диске 448 килобайт?

3.42. Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и 4-битным разрешением. Запись длится полминуты, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

                    1) 8 Кбайт                            2) 240 Кбайт                            З) 0,5 Мбайт                 4) 4 Мбайт

3.43. Производится четырехканальная (квадро) звукозапись с частотой дискретизации 32 кГц и 16-битным разрешением. Запись длится две минуты, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

                    1) 0,5 Мбайт                        2) 7,5 Мбайт                            3) ЗО Мбайт                  4) 240 Мбайт

3.44. Производится одноканальная (моно) звукозапись с частотой дискретизации 8 кГц и 256 уровнями квантования. Запись длится одну минуту, ее результаты записываются в файл, сжатие данных не производится. Какая из приведенных ниже величин наиболее близка к размеру полученного файла?

                    1) 8 Кбайт                            2) 0,5 Мбайт                            З) 128 Мбайт                 4) 1 Гбайт

3.45. Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке.

Вот начало списка:

1.    А.А.А.А.А

2.    А.А.А.АО

                           З . А.А.А.АУ

4. А.ААOА

Запишите слово, которое стоит на 240-м месте от начала списка.

Рекомендация. Задача может быть решена двумя способами: можно увидеть, что общее количество 5-буквенных слов, составленных из трех букв, составляет 35 = 243 и выписывать слова от конца списка. Но это сработает только в том случае, если требуемое по порядку слово близко к концу последовательности (как в этом примере). Существует более универсальный способ. Его идея состоит в том, что такая последовательность слов, записанных в алфавитном порядке при помощи ограниченного количества символов, аналогична системе счисления. Так как в данном случае используется З буквы, это аналогична троичной системе счисления. Поставим в соответствие буквам цифры. Самой первой в алфавитном порядке букве сопоставим О, следующей — 1 , следующей — 2. Получим такую последовательность:

1.  ААААА — 00000

2.  ААААО — 00001

З. ААРАУ — 00002

4.   АФАОА — 00010

При этом заметим, что на позиции 1 стоит число 00000, то есть О, а на позиции 2 — число 00001, то есть 1. Значит, на позиции 240 стоит число 239, записанное в троичной системе счисления. Переведем число 239 в троичную систему (например, будем делить уголком и собирать остатки). Получится 222123. Остается только записать вместо каждой цифры соответствующую букву.

3.46. Все 4-буквенные слова, составленные из букв К, Л, М, Н, записаны в алфавитном порядке. Вот начало списка:

1. кккк 2. кккл

з. кккм 4. кккн

5.  


кклк

Запишите слово, которое стоит на 215-м месте от начала списка.

3.47. Все 4-буквенные слова, составленные из букв П, Р, С, Т, записаны в алфавитном порядке. Вот начало списка:

1. пппп 2. ПППР

з. пппс 4. пппт

5. ППРП

           Запишите слово, которое стоит на 205-м месте от начала списка.

3.48. По каналу связи передаются сообщения, каждое из которых содержит 16 букв А, 8 букв Б, 4 буквы В и 4 буквы Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования:

а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);

б) общая длина закодированного сообщения должна быть как можно меньше.

Какой код из приведенных ниже следует выбрать для кодирования букв А, Б, В и Г?

1)                А:о, Б:10, В:110, Г:111

2)                А:о, Б:10, В:01, Г:11 3) А:1, Б:01, в:011, Г:001

4) А:оо, Б:01, в:10, Г:11

Решение. Способ 1 (в лоб). Для каждого варианта проверить выполнение условия 1 и посчитать длину из условия 2. Условие 1 проверяем так: берем все кодовые слова не максимальной длины и смотрим, не стоят ли они в начале кодов большей длины. В данном примере этому условию не удовлетворяет вариант 2 (кодовое слово «О»/А является началом кодового слова «01 » / В), а также вариант З (кодовое слово «01» /Б является началом кодового слова «011» / В). Для оставшихся вариантов вычисляем суммарную длину сообщения. Вариант 1:

16 • 1 + 8 • 2 + 4 • З + 4 • З = 16 + 16 + 12 + 12 = 56 (16 букв А длины 1 + 8 букв Б длины 2 + 4 буквы В длины З + 4 буквы Г длины З). Вариант 2: 16 • 2 + 8 • 2 + 4 • 2 + 4 • 2 32 + 16 + 8 + 8 = 64. Выбираем вариант 1 как более короткий.

Способ 2. Вычислим количество информации в каждом символе. Всего букв в сообщении 16 + 8 + 4 + 4 = 32. Вычисляем вероятности каждой буквы. А: 16/32 = 1/2, Б: 8/32 = 1/4, В: 4/32 = 1/8, Г: 4/32 = 1/8. Применяем формулу вероятностного подхода к измерению информации i = —loep (буквы-события не равновероятны, поэтому использовать формулу 2 = нельзя). Получаем: А: 1, Б: 2, В: З, Г: З.

Для того, чтобы длина сообщения была наименьшей, длины кодовых слов должны быть равны количеству информации в соответствующем символе. (Вообще говоря, это верно только при таком случае, как здесь — когда вероятности появления букв являются степенями двойки).

Такие длины кодовых слов есть только в варианте 1 и варианте З. Проверяем оба варианта на выполнение условия 1. Вариант З не подходит (кодовое слово «01» /Б является началом кодового слова «011» / В). Получаем, что верный ответ вариант 1.

3.49. По каналу связи передаются сообщения, каждое из которых содержит 64 буквы А, 32 буквы Б, 16 букв В и 16 букв Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования:

а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);

б) общая длина закодированного сообщения должна быть как можно меньше. Какой код из приведенных ниже следует выбрать для кодирования букв А, Б, В и Г?

1) А:11, Б:10, В:01, Г:ОО 2) А:о, Б:10, В:100, Г:110

3)     А:1, Б:01, В:001, Г:ООО

4)     А:1, Б:01, В:10, Г:ОО

3.50. По каналу связи передаются сообщения, каждое из которых содержит 8 букв А, 8 букв Б, 16 букв В и 32 буквы Г (других букв в сообщениях нет). Каждую букву кодируют двоичной последовательностью. При выборе кода учитывались два требования:

а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);

б) общая длина закодированного сообщения должна быть как можно меньше. Какова минимально возможная длина закодированного сообщения?

3.51. По каналу связи передаются сообщения, каждое из которых содержит 100 букв А, 50 букв Б, 25 букв В и 25 букв Г (других букв в сообщениях нет). Каждую букву- кодируют двоичной последовательностью. При выборе кода учитывались два требования:

а) ни одно кодовое слово не является началом другого (это нужно, чтобы код допускал однозначное декодирование);

б) общая длина закодированного сообщения должна быть как можно меньше. Какова минимально возможная длина закодированного сообщения?

3.52. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 30 секунд.

Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 4 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение. Формула для вычисления объема звукового файла: V = Ch • v • i / 8 • t (Число каналов, умноженное на частоту дискретизации, на время записи, на разрешение). Так как разрешение стало в 2 раза выше, а частота дискретизации в 1,5 раза меньше, то объем передаваемых данных стал в 2 раза больше и при этом в 1,5 раза меньше. То есть, изменился в 2/1,5 = 4/3 раза.

Так как пропускная способность канала связи стала в 4 раза выше, то скорость передачи информации стала в 4 раза больше. А значит, время передачи информации будет в 4 раза меньше.

Получаем: исходное время передачи информации (30 секунд) изменится в 4/3/4 раза. Получаем: 30 • 4 / З / 4 = 10 секунд.

3.53. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 40 секунд. Затем тот же музьжальный фрагмент был оцифрован повторно с разрешением в 1,5 раза выше и частотой дискретизации в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 2 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.

3.54. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 50 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в З раза выше и частотой дискретизации в 1,5 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 2 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.

3.55. Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 30 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 1,5 раза ниже и частотой дискретизации в 2 раза больше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б; пропускная способность канала связи с городом Б в 2 раза ниже, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б? В ответе запишите только целое число, единицу измерения писать не нужно.

                                         4. основы ЛОГИКИ        

Основные понятия

В алгебре логики изучаются логические операции, производимые над высказываниями. Высказывания могут быть истинными или ложными. Применяя к простым высказыва, ниям логические операции, можно строить составные высказывания. Основными логическими операциями являются:

1.               Отрицание (инверсия, логическое НЕ)

Смысл операции: результат меняется на противоположный (вместо истины — ложь, вместо лжи — истина). 1:

Обозначение

Таблица истинности:

 

 

 

1

1

 

2.               Логическое сложение (дизъюнкция, логическое ИЛИ)

Смысл операции: результат — истина, если хотя бы один операнд — истина (операндом называется то значение или та переменная, над которым (которой) осуществляется операция).

Обозначение: v

Другое обозначение: + Таблица истинности:

 

в

A v B

 

 

 

 

1

1

1

 

1

1

1

1

з.         Логическое умножение (конъюнкция, логическое И)

Смысл операции: результат — истина, если оба операнда — истина.

Обозначение: л

Другие обозначения: &, Таблица истинности:

 

в

Ал В

 

О

 

О

1

 

1

 

 

1

1

1

Эти три операции считаются базовыми. Остальные рассмотренные нами операции являются дополнительными. Их всегда можно выразить через базовые операции.

1

В различных учебниках информатики обозначения и терминология иногда отличаются. Здесь и далее мы будем применять обозначения и терминологию, используемую в КИМ ЕГЭ.

4.                Следование (импликация)

Смысл операции: из лжи может следовать что угодно, а из истины — только истина.

Обозначение:

 Таблица истинности:

 

 

в

 

 

 

1

 

1

1

1

 

 

1

1

1

5.                Равносильность (эквиваленция)

Смысл операции: результат — истина, если операнды одинаковые.

Обозначение: —

Другое обозначение: е»  Таблица истинности:

 

в

 

 

 

1

 

1

 

1

 

 

1

1

1

6.                Сложение по модулю 2 (исключающее ИЛИ, в просторечье XOR)

Смысл операции: результат — истина, если операнды разные.

Обозначение: О

Таблица истинности:

 

 

в

 

 

 

 

 

1

1

1

 

1

1

1

 

Если в логическом выражении используется несколько логических операций, их порядок определяется приоритетами логических операций:

О) выражение в скобках,

1)  логическое НЕ (инверсия),

2)  логическое И (конъюнкция),

З) логическое ИЛИ (дизъюнкция), исключающее ИЛИ (эти две операции имеют одинаковый приоритет и выполняются слева направо),

4)   следование (импликация),

5)   равносильность (эквиваленция).

Как вы, вероятно, поняли, для изменения порядка выполнения логических операций используются скобки.

Выражение Дополнительных логических операций через базовые операции

Импликация:

Эквиваленция:

—В)

Исключающее ИЛИ:

Основные законы алгебры логики

Название закона

Формулировка

Переместительный закон

AvB=BvA

АлВ=ВлА

Сочетательный закон

Распределительный закон

Закон непротиворечия. Этот закон выражает тот факт, что высказывание не может быть одновременно истинным и ложным

Закон исключенного третьего. Этот закон означает, что либо высказывание, либо его отрицание должно быть истинным

Закон двойного отрицания

Законы де Моргана

Законы переменной с самой собой

Законы нуля и единицы

Av 1 = 1

Законы поглощения

Практическая часть

4.1.        Расставьте над символами логических операций их номера в порядке выполнения операций при вычислении выражения.

                                                                                 в) Ал (В - С) vD

4.2.        Заполните таблицу истинности логических выражений.

 

в

Ал В

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а)

 

в

с

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в

с

-в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

6) в)

 

в

 

 

-в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г)

4.3. Укажите значения переменных А и В, если:

а) Ал В = 1

6) Av B = O

4.4.        Найдите все пары значений А и В, при которых указанное выражение принимает ложное значение.

Пример. Найдите все тройки значения L,N, при которых указанное выражение принимает ложное значение.

Решение:

Из таблицы истинности импликации сразу получаем, что L  Подставляем полученное значение L в выражение в скобках:

1.

Из таблицы истинности дизъюнкции следует, что выражение М v N истинно тогда и только тогда, когда (М = 1, N = О) или (М = О, N = 1) или (М = 1, N 1). Поскольку L О, ответом будут три тройки: (1, - О, М = 1, N = 0), (L = О, М = О, N = 1), (1, = О, М = 1, N = 1).

4.5.        Найдите все тройки значения L, М и N, при которых указанное выражение принимает истинное значение:

Пример. Найдите все целые числа Х, для которых истинно высказывание: (Х > 5) л (Х2 49)

Решение:

Данное составное высказывание истинно, если одновременно истинны оба элементарных сказывания:

х > 5 и х2 <49.

Решив эту элементарную систему неравенств (например, графически), получаем ответ. Ответ: 6; 7.

4.6.        Найдите все целые числа Х, для которых истинно высказывание:

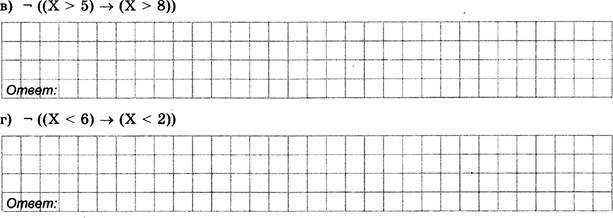
Задания в формате ЕГЭ

Пример 1 . Какое логическое выражение равносильно выражению  3) А ч В л С

Решение.

Логические выражения называются равносильными, если при любых значениях, входящих в них переменных, значения этих выражений равны.

Преобразуем выражение — (А v В) в соответствии с законом де Моргана: — (А v В) = (— А л — В), поэтому правилен ответ под номером 1.

Пример 2. Какое логическое выражение равносильно выражению (А v —С) л л С)? 1) Av-C Л В -С

Решение:

Преобразуем выражение л С) в соответствии с законом де Моргана: л С) = (—(—В) v Ю). Избавимся от двойного отрицания: = (В v —С). Получаем общее выражение: (А v —С) л (В v -С). Но такого выражения нет среди вариантов ответа. Заметим, что в обеих скобках используются одинаковые операции (дизъюнкция) и имеется одинаковая переменная (-С). Вынесем эту переменную за скобки (по распределительному закону): (А л В) v —С. Эго выражение стоит третьим среди вариантов ответа.

4.7 •

а)        Какое логическое выражение равносильно выражению — (— А v В) v С?

2) -Av B v -C

б)       Какое логическое выражение равносильно выражению (— А v В) v С?

                   2) -AvBvC         3) Av -BvC            

в)          Какое логическое выражение равносильно выражению (А v В v С)?

1) AvBvC

г)        Какое логическое выражение равносильно выражению (— А v В) v — С?

              1) - (А л             -С                             2) - Ал - B v -c 3) - Ал вл -С) 4) (А л В) л с

4.8•

а)      Какое логическое выражение равносильно выражению — (А л — С) л В?

                         2) -АлВм -С

б)        Какое логическое выражение равносильно выражению А л — (— В л С)?

1)   - Ал В л - С          2) - Ал - С м В           3) - Ал (В -С) 4) (- Ал В) л с

      в)        какое логическое выражение равносильно выражению — (А л

2)   (В л -C) v Ал - C)

      г)        какое логическое выражение равносильно выражению С л —

      а)      какое логическое выражение равносильно выражению — (А л — С) л В?

1)    -AvC/\B     3) (Ал - C) л -В

2)    -AABv -C    4) -A A B v C AB   

      б)         Какое логическое выражение равносильно выражению А v — С) л

         2) -Av -CABv-C                      4) -AABv -C  

      в)           какое логическое выражение равносильно выражению — (А л В) л - (А л ср

                                                                    3)

         2) -АчВл -С                             4) -AvBA -Av-C

      г)          какое логическое выражение равносильно выражению (А л С) v (А л — С) v

2) Ал(С

а) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения F:

х

 

 

 

 

 

 

 

1

1

 

1

1

 

 

1

Какое выражение соответствует F?

        1) -Xv -Yv -Z         3) X v Y v Z   4) Х л Y A Z

б)        Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения F:

х

 

 

 

 

 

 

1

1

1

 

1

1

 

 

1

Какое выражение соответствует F?

           1) -XA -YA -Z  2) XA -Y/\ -Z     3) XvYv -Z         4) -XvYvZ

в) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Р:

х

 

 

 

 

 

 

 

 

1

 

1

1

 

 

 

Какое выражение соответствует Р?

              1) -XAYA -Z      2) XA -YA -Z       3) XvYv-Z          4) -XvYvZ

г) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Р:

х

 

 

 

 

1

 

 

1

1

1

 

1

 

 

1

Какое выражение соответствует Р?

                    1) -XAYA-Z3) XvYv -Z                4) -XvYvZ

4.11.

а) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Р:

х

У

z

 

о

0

1

1

О

1

О

О

1

о

1

1

Какое выражение соответствует Р?

              1) -Xv -YAZ      2) -XvYvZ         3) -XA -Yv -Z   4) XA -YvZ

б) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: Х, У, Z. Дан фрагмент таблицы истинности выражения Р:

х

У

z

 

о

1

о

1

1

1

о

1

о

О

1

 

Какое выражение соответствует Р?

              1) -XvYA-Z       2) -XvYvZ         3) XA-ZvY      4) -XA-Zv-Y

в) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: А, В, С. Дан фрагмент таблицы истинности выражения Р:

А

в

с

 

О

1

1

1

1

О

1

1

О

1

О

О

Какое выражение соответствует Р?

              1) - Ал В л С                                         3) -АлВм-С                      4) -AvBv -C

г) Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: А, В, С. Дан фрагмент таблицы истинности выражения Р:

А

в

 

 

О

1

1

1

1

1

О

О

О

1

О

1

Какое выраэкение соответствует Р?

               1) - Ал В л - С                  2) -AvBv                        3) АМ В л С                     4) - Ал В М С

а)           Дан фрагмент таблицы истинности выражения Р:

 

 

 

 

х4

 

 

 

 

О

О

1

О

1

О

1

1-

О

1

О

1

1

О

О

О

1

О

1

1

О

1

1

1

Каким из приведенных ниже выражений может быть Р?

1)     — х1         х2 vx3 ч — х4 v х5 v хб v х7

2)     — х1 л — х2 л хЗ л — х4 л х5 л — хб л х7

3)     х1 ч- х2 vx3 Ч - .х4 м- х5 vx6 vx7

4)     х1 л — х2 л хЗ л — х4 л — х5 л хб л х7

б)       Дан фрагмент таблицы истинности выражения Р:

 

 

 

х4

 

 

 

 

О

1

О

О

1

О

1

 

О

1

1

О

1

о

О

О

1

О

1

О

о

1

1

1

Каким из приведенных ниже выражений может быть Р?

1) — х1 v — х2 v хЗ v — х4 v х5 v — хб v х7 2) — х1 л — х2.л хЗ л — х4 л х5 л — хб л х 7

З) х1 v х2 v хЗ v х4 v х5 v хб v х7

4) х1 л — х2 л хЗ л — х4 л — х5 л хб л х7

в)          Дан фрагмент таблицы истинности выражения F:

 

 

 

х4

 

 

 

 

О

О

1

О

1

О

1

1

О

1

О

1

1

О

О

1

1

О

1

1

О

1

1

 

Каким из приведенных ниже выражений может быть Р?

1) — х1 v х2 v — хЗ v — х4 v х5 v— хб v х7 2) х1 л х2 л хЗ л — х4 лх5 л — хб л — х7

              З)    .x1-v — х2 vx3 v — х4 v— х5 v хб v х7

4) — х1 л — х2 л хЗ л — х4 л — х5 л хб л х7

г)          Дан фрагмент таблицы истинности выражения F:

 

 

 

х4

 

 

 

 

О

О

1

О

1

О

1

 

О

1

О

1

1

О

о

О

1

о

1

1

О

1

1

 

Каким из приведенных ниже выражений может быть F?

1)    х 1 v— х2 v хЗ v х4 v — х5 v хб v х7         

2)    х1 л — х2 л хЗ л х4 л — х5 л хб л х7


                       З) Х1 V— Х2 V хЗ                Х4              Х5 VX6 V Х 7

4) х1 л — х2 л хЗ л — х4 л — х5 лхб л х7

Пример. Найдите наименьшее целое число Х, при котором истинно высказывание

Решение.

Импликация истинна в трех случаях:

1) О 1 (ложь истина)         2) О О (ложь ложь)           З) 1 —» 1 (истина истина) Рассмотрим 1-й случай:

Предположим, что (Х > 7) v (Х < 7) = ложь и Х > 8 = истина.

(Х > 7) v (Х < 7) = ложь только при Х = 7. 7 < 8, поэтому в данном случае решения нет.

Рассмотрим 2-й случай:

Предположим, что (Х > 7) v (Х < 7) = ложь и Х > 8 = ложь. В этом случае Х = 7 является единственным решением.

Рассмотрим 3-й случай:

Предположим, что (Х > 7) v (Х < 7) = истина, тогда Х — любое целое число, кроме 7.

Из условия Х > 8 получаем, что наименьшим решением будет 9. Но во втором случае мы получили решение 7. 7 < 9, поэтому окончательный ответ: 7.

Второй вариант решения

Для начала приведем выражение в более удобную форму, вспомнив, что (Х > 7 ИЛИ Х < 7) в математике записывается как Х 7. (Х 7) (Х > 8).

Преобразуем данное выражение по законам алгебры логики.

Воспользуемся законом «А В - А В». (Х 7) (Х > 8) (Х = 7) (Х > 8). Таким образом, решением является число 7 и все числа больше 8. Наименьшим из этих чисел является число 7.

4.1 з•

а)          Найдите наименьшее целое число Х, при котором истинно высказывание:

б)          А, В, С — целые числа, для которых истинно высказывание:

в)          Каково наибольшее целое число Х, при котором истинно высказывание:

г)          Укажите наименьшее целое число Х, для которого истинно высказывание:

4.14.

а)          Для какого слова истинно высказывание:

— (Первая буква слова согласная (Вторая буква слова гласная v Последняя буква слова гласная))?

              1) ГОРА                          2) БРИКЕТ                     3) ТРУБКА                     4) ПАРАД

б)          Для какого слова ложно высказывание:

Первая буква слова согласная (Вторая буква слова гласная л Последняя буква слова гласная)?

              1) ЖАРА                         2) ОРДА                         3) ОГОРОД                     4) ПАРАД

в)          Для какого слова истинно высказывание:

— (Первая и последняя буквы слова согласные       Первая и последняя буквы слова совпадают)?

                1) комок                        2) ПРИВЕТ                     3) ТРУБКА                      4) окно

г)          Для какого слова ложно высказывание:

Первая буква слова гласная (Вторая буква слова гласная v Последняя буква слова гласная)?

               1) ЖАРА                          2) ОРДА                           3) ОГОРОД                      4) ПАРАД

4.15. Найдите значения логических переменных А, В, С, D, при которых указанное логическое выражение ложно. Ответ запишите в виде строки из четырех символов: значений переменных А, В, С и D (в указанном порядке). Так, например, строка 0101 соответствует 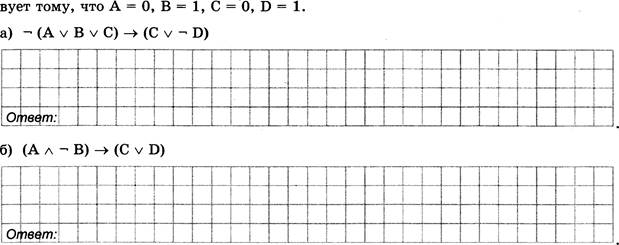тому, что А = О, В —

Пример. Сколько различных решений имеет уравнение

(К v L v М) (L л - мл N) = О, где К, L, М, N — логические переменные?

Решение.

Из таблицы истинности дизъюнкции следует, что

Из таблицы истинности дизъюнкции следует, что (К v L v М) = О тогда и только тогда, когда К = О, = О, М = О.

Подставив найденные значения переменных в уравнение (L л —М л N) = О, получаем

(О л 1 л N) = О. Конъюнкция О с любым значением равна О, поэтому решением данного уравнения будет любое значение N.

Учитывая ранее найденные значения К, L, М, получаем 2 решения: (К = О, L = О, М = О,

Ответ: 2.

4.16. Сколько различных решений имеет указанное уравнение, где К, L, М, N — логические переменные?

В ответе не нужно перечислять все различные наборы значений К, L, М и N, при которых выполнено данное равенство. В качестве ответа вам нужно указать только количество таких наборов.

а)

6) в)

г)

Пример. Сколько различных решений имеет система уравнений:

(х1 л               --х1 л -и) (хехз) =

(Х2 л                                 -Х2 л -хз) (XFX4) —

(хз л .Х4 v —хз л -%4) (хз%Х5) ¯

(х4 л х5 v —.х4 л -%5) v (хеХ6) — (Х5 л .Х6 V —Х5 л —Х6) V (Х5ЕХ7) где х1, .х2, хз, ..., — логические переменные?

Знаком обозначена логическая операция «эквивалентность» (результат истина, если операнды одинаковы). В ответе не нужно перечислять все различные наборы значений х1, х2, хз, ..., х8, при которых выполнена данная система уравнений. В качестве ответа нужно указать количество таких наборов.

Решение:

Сначала попробуем привести уравнения к более удобному виду. В частности, можно заметить, что в первой скобке каждого уравнения находится логическое выражение, равносильное эквиваленции.

Если для Вас подобное преобразование сразу не очевидно, но вы видите, что между двумя переменными производятся сложные логические преобразования, постройте таблицу истинности для этих двух переменных и посмотрите, какая получится таблица истинности. Весьма вероятно, что она совпадет с таблицей истинности эквиваленции (как в данном случае) или ее отрицания (исключающего ИЛИ).

Заменив выражения в первых скобках на эквиваленции, получим:

(хрх2) v (Х1ЕХз)

( Х2ЕХз) (X FX4)

(XFX4) (хз=Х5)1

(хеХ5) v (хеХ6)1

(Х*Х6) v (Х5*7) - 1

Дальнейшее решение построим на принципе рассуждений. Будем предполагать, что переменная равна определенному значению, и смотреть, что из этого следует. Пусть х1 = 1.

Пусть х2 = О. Тогда первое условие первого уравнения не выполняется (х1*х2) и тогда должно выполняться второе условие первого уравнения (ХЁХз). То есть хз = 1. Тогда получается, что .х2 хз (не выполняется первое условие второго уравнения), значит, должно выполняться второе условие второго уравнения (х2±х4). Значит, .х4 = О. Аналогично рассуждая, получаем, что значения последующих переменных должны чередоваться: х5 —  1. Эта ветка рассуждений (х1 = 1, х2 О) привела нас к единственному решению. Запомним его (1).

Пусть х2 = 1. Тогда первое условие первого уравнения выполняется (XFX2). Это значит, что второе условие первого уравнения (ХЁХз) не обязательно должно выполняться. То есть хз может быть любым.

Пусть .хз = О. Тогда первое условие второго уравнения (Х2ЕХз) не выполняется. Значит, должно выполняться второе условие второго уравнения (хеХ4). То есть .х4 = 1. Ситуация аналогична уже рассмотренной нами для х2 = О значения последующих переменных должны чередоваться: х5 — О, х6 — 1, = О, Это единственное решение. Запомним его (1).

Пусть .хз = 1. Тогда первое условие второго уравнения выполняется (Х2ЕХз). Это значит, что второе условие второго уравнения (х2±х4) не обязательно должно выполняться. То есть, .х4 может быть любым.

Мы пришли к повторяющейся ситуации. Для каждой последующей переменной если она будет равна нулю, это будет давать единственное решение, а если единице, то нуж но будет рассматривать два варианта значений следующей переменной. Получается, для каждой переменной .х2 ... .х7 имеется единственное решение (с чередующимися значениями остальных переменных). Плюс у последней пепеменной возможно два значения (2). Всего получается 7 возможных вариантов (для исключения ошибки рекомендуем аккуратно расписать все эти предположения для каждой переменной и потом посчитать «запомненные» (1) и (2)).

Нетрудно понять, что для х1 = О ситуация совершенно аналогична (симметрична), и это дает нам еще 7 вариантов. Ответ: 14.

4.17•

а)          Сколько различных решений имеет система уравнений:

—х2) v (хрхз) - 1

(Х2 л .хз v          

—хз) v (Х22Х4) — 1

               (хз л                     —х4) v (хз=Х5) — 1

—Х5) V (XFX6) — 1

—Х6) v (Х52Х7) - 1

—хт) v (Х6>Х8) — 1

где х1, Х2, хз, ..., .t8 — логические переменные?

6)         Сколько различных решений имеет система уравнений:

-И) (хехз)

(Х2 л хз v   

—хз) V (XFX4) —

(хз л Х4 v   

—Х4) v (хз=Х5)                           

—х5) v (хеХ6)

—Х6) V (Х5ЕХ7) .Х6±Х8 = 1  где % , х2, хз, ..., х8 — логические переменные?

в)             Сколько различных решений имеет система уравнений:

(х1бх2) v (х2 л .хз v —Х2 л —хз) —

(Х2Охз) v (хз л х4 v —хз л —х4) —

(хзОХ4) v (Х4 л х5 v —Х4 л —Х5) —

(Х4ОХ5) v (Х5 л .Х6 —Х5 л -%6) — (Х56Х6) v (Х6 л .Х7 v —Х6 л —Х7) — (Х6ОХ7) v (Х? л v где х1, х2, хз, ..., .х8 — логические переменные?

           Сколько различных решений имеет система уравнений:

(ХIОХ2) v (ХIОхз) ¯

(Х2Охз) v (Х2ОХ4)

(хзОХ4) v (хзОХ5)

(Х4ОХ5) v (Х4ОХ6) —

(Х5ОХ6) v (30х7)

(Х6ОХ7) v (Х6ОХ8) — где х1, х2, хз, ..., х8 — логические переменные?

4.18. Миша заполнял таблицу истинности для выражения Р. Он успел заполнить лишь небольшой фрагмент таблицы:

 

х2

 

х4

 

 

 

х8

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

 

 

1

 

 

 

1

 

 

 

 

 

Каким из приведенных ниже выражений может быть F?

1)  х 1 л —х2 л хЗ л —х4 л х5 л хб л —х7 л —х8

2)  —х1 л х2 л —хЗ л х4 л х5 л хб л х7 л х8

З) х 1 v х2 v — хЗ v х4 v х5 v —хб v х7 v х8

4)   х1 v —х2 v хЗ v —х4 v —х5 v хб v —х7 v —х8

Рекомендация. Среди вариантов ответа обнаруживаем только либо сплошные конъюнкции, ли60 сплошные дизъюнкции. Смотрим на столбец результата (F) и видим там две единицы. Значит, это не может быть конъюнкцией. Значит, это дизъюнкция. дизъюнкция дает в результате один единственный ноль тогда и только тогда, когда складываются все нули. В строке З приведенной таблицы имеем ноль. Чтобы складывались все нули, нужно, чтобы переменные х1 и х4 (только для них указаны значения) были х1 и ах4 (переменная х1 уже 0, а переменная х4 равна 1, складывать нужно только нули, поэтому х4 должна быть инвертирована). Ищем среди вариантов ответа дизъюнкцию (варианты З и 4), в которой х1 и —х4. Это вариант 4.

Если бы в столбце F были бы два нуля и одна единица, ответ нужно было бы искать среди коньюнкций, причем в той строке, к которой получается единственная 1, нужно чтобы все переменные были равны 1. Те переменные, которые в этой строке даны равными 0, нужно было бы инвертировать.

4.19 •

а) Миша заполнял таблицу истинности для выражения Р. Он успел заполнить лишь небольшой фрагмент таблицы:

х1

х2

хЗ

х4

 

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

1

 

1

 

 

1

 

 

 

 

 

 

Каким из приведенных ниже выражений может быть Р?

1)   х 1 л —х2 л хЗ л —х4 л х5 л хб л —х7 л —х8

2)   —х1 л —х2 л —хЗ л х4 л х5 л хб л х 7 л х8

З) —х1 v х2 v —хЗ v —х4 v х5 v хб v х7 v х8

4) х1 v —х2 v хЗ v —х4 v —х5 v хб v —х7 v —х8

б) Миша заполнял таблицу истинности для выражения F. Он успел заполнить лишь небольшой фрагмент таблицы:

х1

х2

хЗ

 

х5

 

 

х8

 

1

 

 

1

 

 

 

 

1

 

 

 

 

1

 

 

 

 

 

 

1

 

 

 

 

 

1

Каким из приведенных ниже выражений может быть Р?

1)  —х1 v х2 v хЗ v х4 v х5 v хб v х7 v х8

2)  х1 л х2 л хЗ л х4 л х5 л —хб л —х7 л —х8

          З) х 1 v х2 v хЗ v —х4 v —х5 v хб v —х7 v —х8

4) —х1 л —х2 л —хЗ л х4 л х5 л хб л х7 л х8

в) Миша заполнял таблицу истинности для выражения Р. Он успел заполнить лишь небольшой фрагмент таблицы:

х1

х2

хЗ

х4

 

 

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

1

 

 

 

 

1

Каким из приведенных ниже выражений может быть Р?

1)  —х1 л —х2 л хЗ л х4 л —х5 л —хб л х 7 л х8

2)  х1 v —х2 v хЗ v —х4 v —х5 v —хб v —х7 v —х8

              З) —х1 v х2 v хЗ v х4 v х5 v хб v х7 v х8

4)   х1 л х2 л хЗ л х4 л х5 л —хб л —х7 л —х8

4.20. На числовой прямой дан отрезок В = [4, 12]. Выберите такой отрезок А, что формула (х е А) v — (х Е В) верна при любых значениях х.

           1) [5, 10]                                                     3) [2, 15]                    4) [20, 25]

Решение. Нарисуем на числовой прямой область, которая нам известна. Это отрезок В. Найдем части числовой прямой, для которых приведенное условие точно выполняется. Так как логические выражениея (х А) и — (х е В) связаны дизъюнкцией, области, для которых результат будет истинным, должны объединяться. Значит, для всех точек числовой прямой, для которых одно из выражений будет истинным, общее выражение тоже будет истинным. Заштрихуем те точки числовой прямой, для которых выполняется условие — (х В). Так как перед скобкой стоит отрицание, это будут все точки, которые НЕ входят в отрезок В:

в

Незаштрихованными остались точки отрезка В. При объединении с отрезком А эти точки должны стать заштрихованными. Значит, все точки отрезка В должны целиком находиться внутри отрезка А. Осталось выбрать такой отрезок А, левая граница которого меньше левой границы отрезка В, а правая граница больше правой границы отрезка В.

Разберем все возможные комбинации этой задачи:

а) (х Е А) v — (х Е В). Разобран выше. Огрезок В должен целиком находиться внутри отрезка А: в

б) — (х е А) v (х Е В). Известно, что для всех точек отрезка В формула истинна. Значит, нужно, чтобы «—А» «покрыло» всё оставшиеся незаштрихованные области. Для этого отрезок А должен целиком находиться внутри отрезка В.

в

в) — (х Е А) v — (х Е В). Заштрихованными оказываются все точки, не входящие в В. Значит, «—А» должен «покрывать» отрезок В. Для этого нужно, чтобы ни одна точка отрезка А не находилась на отрезке В.

в

Если исходная формула не такая простая, нужно привести ее к этому виду. Для этого:

1)                если встречается операция —», преобразуйте ее по закону: А В =         v В;

2)                если отрицание стоит перед скобкой, в которой л или v: примените закон де Моргана и уберите отрицание перед скобкой v В) = —А л —В, —(А л В) = —А v —В).

После этого:

1)                нарисуйте на числовой прямой оставшиеся области,

2)                заштрихуйте соответствующие им области (внутри отрезка, если нет отрицания, или снаружи отрезка, если есть отрицание),

З) области, объединенные операцией v, штрихуйте в одну сторону и считайте результатом все, куда попала хотя бы одна штриховка,

4)                 области, пересеченные опарацией л, штрихуйте в разную сторону и считайте результатом только то, где обе штриховки пересеклись.

В результате задача сведется к одному из случаев а), б) или в), разобранных нами ранее.

4.21.   На числовой прямой дан отрезок В = [4, 12]. Выберите такой отрезок А, что формула — (х Е А) v (х Е В) верна при любых значениях х.

1)    [5, 10]    3) р, 15]      4) [20, 25]  

4.22.   На числовой прямой даны отрезки В = [2, 12] и С = [7, 18]. Выберите такой отрезок А, что формула (х Е А) v ((х Е В) (х Е С)) верна при любых значениях х.

                                            2) [6, 14]                                                     4) [5, 20]

4.23.   На числовой прямой даны отрезки В = [2, 12] и С = [7, 18]. Выберите такой отрезок  А, что формула — (х Е А) v — ((х е В) (х Е С)) верна при любых значениях х.

1)    [1, 20]    2) [6, 14]     4) [8, 10]

4.24.   На числовой прямой даны отрезки В = [2, 12] и С = [7, 18]. Выберите такой отрезок А, что формула (х Е А) — (— (х е В) л — (х е С)) верна при любых значениях х.

1)    [1, 20]       2) [13, 16]     4) [8, 20]

 4.25. На числовой прямой даны отрезки В = [2, 12] и С = [7, 18]. Выберите такой отрезок А, что формула (— (х Е В) (х Е С)) — (х Е А) верна при любых значениях х.

               1) р, 25]                           2) [8, 11]                          3) [1, 20]                              4) [6, 15]

4.26. Каждое из логических выражений А и В зависит от одного и того же набора из 5 переменных. В таблицах истинности обоих выражений в столбцах значений стоит ровно по 4 единицы в каждой таблице. Каково минимально возможное число единиц в столбце значений таблицы истинности выражения Av—B?

Решение.

5

Таблица истинности содержит 2 — 32 строки. Поскольку в таблице истинности значения могут быть только О или 1, в столбцах значений для выражения —В содержится 28 единиц и 4 нуля. Выражение Av—B истинно, если хотя бы одно из выражений А или —В истинно. Минимально возможное число единиц в столбце значений таблицы истинности выражения Av—B достигается, когда нулевые значения выражения В сочетаются с нулевыми значениями выражения А. Поскольку нулевых значений выражения А заведомо больше четырех, искомый минимум равен 28.

4.27• Каждое из логических выражений А и В зависит от одного и того же набора из 8 переменных. В таблицах истинности обоих выражений в столбцах значений стоит ровно по 5 единиц в каждой таблице. Каково минимально возможное число нулей в столбце значений таблицы истинности выражения АлВ?

4.28 • Каждое из логических выражений А и В зависит от одного и того же набора из 7 переменных. В таблицах истинности обоих выражений в столбцах значений стоит ровно по 10 единиц в каждой таблице. Каково минимально возможное число нулей в столбце значений таблицы истинности выражения АлВ?

4.29В Каждое из логических выражений А и В зависит от одного и того же набора из 7 переменных. В таблицах истинности обоих выражений нет ни одной совпадающей строки. Сколько единиц будет содержаться в столбце значений таблицы истинности выражения АлВ?

 Каждое из логических выражений А и В зависит от одного и того же набора из 7 переменных. В таблицах истинности обоих выражений нет ни одной совпадающей строки. Сколько единиц будет содержаться в столбце значений таблицы истинности выражения AvB?

 Обозначим через ДЕЛ(п, т) утверждение «натуральное число п делится без остатка на натуральное число т».

Для какого наибольшего натурального числа А формула -ДЕЛ(х, А) (ДЕЛ(х, 6) -ДЕЛ(х, 4) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Решение.

Упростим выражение. Избавимся от операции импликация, смысл которой с точки зрения арифметики выразить затруднительно. По формуле А В = —А v В получаем:

ДЕЛ(х, А) (-ДЕЛ(х, 6) -ДЕЛ(х, 4))

Так как смысл выражения (—ДЕЛ(х, 6) v —ДЕЛ(х, 4)) все еще трудно понять, применим закон Де Моргана (вынесем отрицание за скобки). Получим —(ДЕЛ(х, 6) л ДЕЛ(х, 4)). Выражение в скобках означает, что число х одновременно делится на 6 и на 4. Это значит, что оно делится на наименьшее общее Кратное чисел 6 и 4. То есть, на число 12. Получаем общее выражение:

ДЕЛ(х, А) -ДЕЛ(х, 12)

Выражение —ДЕЛ(х, 12) дает нам все числа, которые не делятся на 12. Так как общее выражение должно быть верно для всех натуральных х, к этим числам не хватает только тех, которые делятся на 12. Выражение ДЕЛ(х, А) — все числа, делящиеся на А. Значит, нужное нам наибольшее значение А равно 12.

4.32. Обозначим через т&п поразрядную конъюнкцию неотрицательных целых чисел т и

п. Так, например, 11 & 6 = 10112 & 01102 = 00102

Для какого наибольшего неотрицательного целого числа А формула  х&А # О (х&1О = О х&б # О) тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Решение.

Упростим выражение. Избавимся от операции импликация. Получаем: хи = o v (х&10 0)

Проанализируем, что означает выражение х&1О О. 10 = 10102. После поразрядной коньюнкции числа х с числом 10102 из двоичного представления числа х все его двоичные цифры станут равны О, кроме тех, которые стоят на позициях единиц в числе 10102. То есть, результат будет не равен нулю, если в двоичном представлении числа х на позициях номер 1 и З (нумерация справа налево начиная с нуля) стоит хотя бы одна единица. А для выражения х&б О это будет для позиций 1 и 2 (6 = 1102).

Значит, выражение (х&1О О v х&б О) будет истинно, если в двоичном представлении числа х есть хотя бы одна единица на позициях 1, 2 или З. Это можно иначе записать как х&111О2 О. То есть, х&14 О. Получаем выражение: х&А = О v х&14 О. Правая часть выражения истинна, если хотя бы на одной из позиций 1,2 или З в числе х стоит единица. Значит, чтобы выражение было истинно для любых х, нужно добавить все такие числа, у которых на этих позициях стоят нули. Наибольшее число, которое может быть подставлено в условие х&А = О для достижения такого результата — это само число 14.

4.33• Обозначим через ДЕЛ(п, т) утверждение «натуральное число п делится без остатка на натуральное число т».

Для какого наибольшего натурального числа А формула

 (ДЕЛ(х, 6) -ДЕЛ(х, 9)) ДЕЛ(х, А) тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

4.34. Обозначим через                  поразрядную конъюнкцию неотрицательных целых чисел т и

                п. Так, например, 11&6 = 10112&01102 = 00102 = 2

Для какого наибольшего неотрицательного целого числа А формула О (х&12 = О .х&5 0) тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Обозначим через т&п поразрядную конъюнкцию неотрицательных целых чисел т и

п. Так, например, 11 & 6 = 10112 & 01102 — 00102 - 2.

Для какого наибольшего неотрицательного целого числа А формула

тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

5. АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ

Основные понятия

Тема «Алгоритмизация и программирование» наиболее. широко представлена в ЕГЭ по информатике. Для успешного выполнения заданий этой темы нужно знать и уметь использовать на практике основные алгоритмические конструкции:

•       следование;

•       полное и неполное ветвление;

•       цикл с предусловием;

•       цикл с постусловием;  цикл с заданным числом итераций;  вспомогательный алгоритм (подпрограмма).

Необходимо уметь составлять, анализировать и выполнять алгоритмы, используя различные формы записи:

•       естественный язык;

•       графический язык (блок-схемы);  формальный язык (язык программирования).

Требуется также уметь использовать простые структуры данных — одномерные и двумерные массивы.

Практическая часть

5.1.        Программа для некоторого арифметического устройства представляет собой последовательность символов «+» и « ». Символ «+» означает прибавление единицы к текущему результату вычислений, « • — умножение на 2. Выполнение программы производится слева направо. Найдите результат работы устройства для заданного исходного числа и программы:

а)       

б)         

в)       

г)               2008

5.2.        Составьте для устройства, описанного в предыдущем задании, программу, длиной не более 6 символов, преобразующую заданное исходное число в заданный результат:

а)         из О получить 17.

Ответ: б)            из З получить 30.

Ответ: в)            из —5 получить 30.

Ответ: г)            из —2 получить 5.

Ответ:

Рассмотрим пример решения задачи с исполнителем РОБОТ.

Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:

вверх

вниз

влево

вправо

При выполнении этой команды РОБОТ перемещается на соответствующую клетку.

Команды проверки истинности условия на наличие стены у той клетки, где он находится:

сверху свободно

снизу свободно

слева свободно

справа свободно

Если РОБОТ начнет движение в сторону стены, то он разрушится.

а) Сколько клеток данного лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?

НАЧАЛО8

                      ПОКА справа свободно                                                                                         7

ДЕЛАТЬ вправо6

ПОКА снизу свободно5

ДЕЛАТЬ вниз4

ПОКА слева свободноз

ДЕЛАТЬ влево2

1

ПОКА сверху свободно

A B C D E F G H

ДЕЛАТЬ вверх

КОНЕЦ

В ответе запишите число количество таких клеток, а далее, через запятые, их адреса (сначала идет латинская буква столбца, а затем цифра строки). Например, нижний левый угол лабиринта имеет адрес А 1.

Решение.

Сначала определим свойства клеток, отвечающих требованию задачи. Поскольку последний цикл программы РОБОТА

ПОКА сверху свободно ДЕЛАТЬ вверх

искомые клетки должны иметь границу сверху.

Таких клеток 14: вся верхняя горизонталь 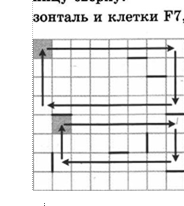и клетки F7, G6, В4, Н4, Е2 и Н1.

Предпоследний цикл программы РОБОТА

ПОКА слева свободно ДЕЛАТЬ влево

Это значит, что в вертикали искомой клетки ниже нее обязательно должна быть клетка с левой границей, от которой «отскочил» РОБОТ перед тем, как пойти вверх. Из ранее найденных клеток этому условию удовлетворяют 4 — А8, В8, В4, G6.

При этом В8 надо тоже отбросить, поскольку в ее вертикали на пути от клетки В2 стоит горизонтальная граница между В4 и В5.

Далее используем остальные фрагменты программы. Выполнив программу целиком для трех оставшихся клеток, получаем, что условию задачи удовлетворяют только две из них А8 и В4.

Ответ: 2, А8, В4.

5.3. Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:

вверх

вниз

влево

вправо

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз Ь, влево е, вправо

Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:

сверху свободно

снизу свободно

слева свободно

справа свободно

Цикл

ПОКА < условие > команда выполняется, пока условие истинно, иначе происходит переход на следующую строку. Если РОБОТ начнет движение в сторону стены, то он разрушится и программа прервется.

Нарисуйте путь РОБОТА в лабиринте, если он начал движение по программе из указанной клетки.

Лабиринт

Программа

Начальная клетка

6

5 4 з 2

1

A B C D E F

НАЧАЛО

ПОКА < справа свободно > вправо

ПОКА < снизу свободно > вниз

ПОКА < слева свободно > влево ПОКА < сверху свободно > вверх

КОНЕЦ

 

а)

Лабиринт

Программа

Начальная клетка

6

5

4

3

2

1

A B C D E F

НАЧАЛО

ПОКА < слева свободно > влево

ПОКА < сверху свободно > вверх

ПОКА < справа свободно > вправо

ПОКА < снизу свободно > вниз

КОНЕЦ

 

б)

Лабиринт

Программа

Начальная клетка

6

5

4

3

2

1

A B C D E F

НАЧАЛО

ПОКА < слева свободно > влево

ПОКА < сверху свободно > вверх ПОКА < справа свободно > вправо

ПОКА < снизу свободно > вниз

КОНЕЦ

 

в)

Лабиринт

Программа

Начальная клетка

6

5 4 з 2

1

A B C D E F

НАЧАЛО

ПОКА < слева свободно > влево

ПОКА < справа свободно > вправо ПОКА < снизу свободно > вниз ПОКА < сверху свободно > вверх

КОНЕЦ

г)

5.4. Для исполнителя РОБОТ, описанного в предыдущем задании, составить программу не более чем из семи строк (включая строки «НАЧАЛО» и «КОНЕЦ»), обеспечивающую нужное перемещение по заданному лабиринту

Лабиринт

Программа

Начальная клетка

Конечная клетка

A B C DE F

 

 

 

а)

Лабиринт

Программа

Начальная клетка

Конечная клетка

A B C D E F

 

 

 


б)

Лабиринт

Программа

Начальная клетка

Конечная клетка

A B O D E F G H

 

 

в)

Лабиринт

Программа

Начальная клетка

Конечная клетка

A B C D E F G H

 

г)

для решения задач на определение значения переменной после выполнения фрагмента программы или блок-схемы удобно использовать таблицу значений переменных.

Пример. Дана блок-схема алгоритма. Требуется найти значение переменной с после завершения алгоритма.

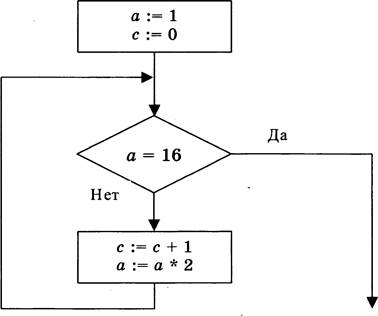
Решение.

1-й способ

Составим таблицу значений переменных, добавив в нее для удобства результаты вычисления логического выражения.

N2 шага

Значение а

Значение с

а = 16 ?

 

1

 

нет

1

1

1

 

2

2

1

нет

з

2

2

 

4

4

2

нет

5

4

з

 

6

8

з

нет

7

8

4

 

7

16

4

да

Итак, ответ с = 4,

2-й способ

Внимательно проанализировав блок-схему, можно заметить, что она иллюстрирует последовательное удвоение переменной а, изначально равной единице, до тех пор, пока она не достигнет значения 16 = 24 . Отсюда с = log2 16 = 4.

5.5. Впишите во фрагмент блок-схемы пропущенные инструкции, необходимые для правильного решения поставленной задачи.

а)        Найти минимальный элемент массива М из 24 элементов.

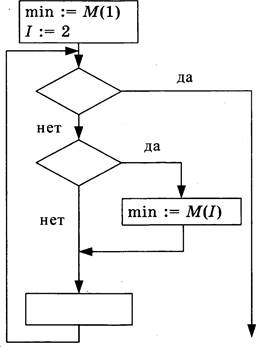
б)       Найти сумму отрицательных элементов массива М из 24 элементов,

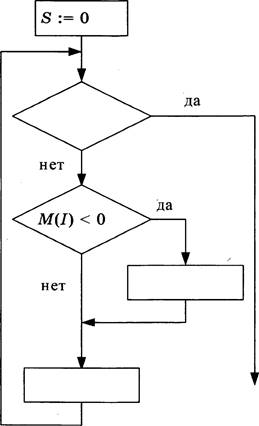
в) Найти сумму положительных элементов массива М из 22 элементов, имеющих четные номера (нумерация элементов массива начинается с единицы).

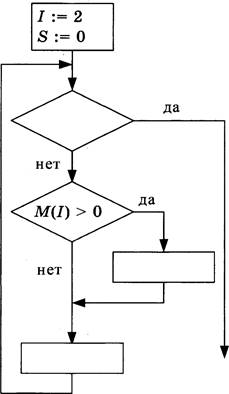
г) В массиве М 45 элементов. Найти сколько подряд идущих элементов этого массива, начиная с первого, образуют возрастающую последовательность.

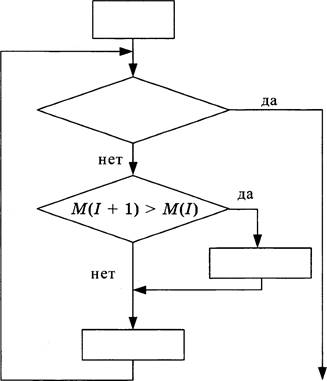
5.6. Составить и записать на естественном языке алгоритм, выполняющий:

             а)        решение уравнения ах = Ь, где а и Ь — числовые исходные данные;

б) поиск количества минимальных элементов в заданном целочисленном массиве из 50 элементов;

             в)       поиск наибольшего общего делителя двух натуральных чисел;

               г)                  поиск количества простых чисел в заданном целочисленном массиве из 50 элементов.

5.7. Составить и записать в виде блок-схемы алгоритм, выполняющий:

               а)        решение уравнения ах = Ь, где а и Ь — числовые исходные данные;

               6)       поиск количества минимальных элементов в заданном целочисленном массиве из

50 элементов;

       в)       поиск наибольшего общего делителя двух натуральных чисел;

       г)       поиск количества простых чисел в заданном целочисленном массиве из 50 элементов.

Замечание. В задачах на определение результатов выполнения программы для одномерных и двумерных массивов необходимо определить закономерность обработки массива, поскольку его размерность может быть задана переменной величиной, а не конкретным значением.

Однако, для того чтобы понять эту закономерность, иногда требуется выполнить несколько итераций цикла «вручную», используя табличное представление массива.

Пример. Значения двумерного массива размера п х п задаются с помощью вложенного опе ратора цикла в представленном фрагменте программы.

Бейсик

Паскаль

Алгоритмический

FOR                 ТО п

FOR К=1 ТО п

IF                 THEN

A(i, k) — FJLSE

END IF

NEXT К

NEXT п

for i:=1 to п do for К:=1 to п do if i=k then

else

для от 1 до п для К от 1 до п если i=k то

иначе

все

кц

Как будет зависеть от п сумма элементов массива А после выполнения алгоритма?

Решение.

Изобразим двумерный массив в виде таблицы. На диагонали таблицы, там, где — i, будут находиться двойки. В остальных ячейках — нули.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

п—1

 

 

 

 

 

 

 

 

 

 

 

 

 

Количество элементов диагонали — п, поэтому сумма элементов массива будет равна 2n. Ответ: 2n.

5.8. Выполнить фрагмент программы и найти итоговые значения переменных:

Бейсик

Паскаль

Алгоритмический

а=12З4

MOD 1000) * 10 a=a\1000+b

'\ и MOD — операции, вы— числяющие результат де— ления нацело первого аргумента на второй и остаток от деления со— ответственно

Ь: = (а mod 1000) * 10; а :=а div 1000+b; { div и mod операции, вычисляющие результат деления нацело первого аргумента на второй и остаток от деления со— ответственно }

b:=mod (а, 1000) * 10 a :=div (а, 1000) +b div и mod функции, вычисляющие результат деления нацело первого аргумента на второй и остаток от деления со— ответственно

а)

Бейсик

 

Паскаль

 

Алгоритмический

а=12З4

( а МОГ) 10) *

1000

Ь: = (а mod 10) * а:=а div 10+b;

1000;

Ь: =mod (а, 10) * 1000 а : =div (а, 10) +b

б)

Бейсик

Паскаль

Алгоритмический

MOD 3) +15

— (7—5) * 4; mod 3) +15; div 4) +3

Ь : =mod (а, 3) +15 a:=div (Ь,

в)

Бейсик

Паскаль

Алгоритмический

(6+2) * 4

MOD 5) +1

а: = (6+2) * 4;

Ь: = (а mod 5) +1; div 6) -2

Ь: =mod (а, а: =div (Ь,

г)

5.9.

       а)       Дан фрагмент программы, обрабатывающей массив А из 10 элементов:

 

Бейсик

Паскаль

Алгоритмический

п=10

FOR i

A(i) =i

NEXT

1

1 то п

1 то П-1

 THEN Ј-Ј+1

п=10; for i:=1 to п do

for i :=1 to п— 1 do

then Ј

п :=10 нц для i от 1 до п

нц для i от 1 до п-1 если A[i] то

Ј=Ј+1 все

Чему будет равно значение переменной ј после выполнения данного алгоритма?

Ответ:

       б)       Дан фрагмент программы, обрабатывающей массив А из 10 элементов:

 

Бейсик

Паскаль

Алгоритмический

п=10

FOR

FOR i

NEXT

1 то п

- 1 то п

THEN

п=1О; for i :=1 to п do

s:=O; for i :=1 to п do if i>5 then

нц для i от 1 до п 11—1

s:=O нц для i от 1 до п то s=s+A[i] все кц

                       Чему будет равно значение переменной s после выполнения данного алгоритма?

Ответ:

              в)       Дан фрагмент программы, обрабатывающей массив А из п элементов:

 

Бейсик

Паскаль

Алгоритмический

FOR

IF ј

NEXT I

2 то п

THEN

for i:=2 to п do if j<A[i] then ј .

нц для i от 2 до п если j<A[i] то

все

Как зависит итоговое значение переменной ј от значений массива А?

Ответ:

              г)       Дан фрагмент программы, обрабатывающей массив А из п элементов:

 

Бейсик

Паскаль

Алгоритмический

Ј          О

FOR

IF

NEXT I

1 то п

THEN Ј-Ј+1

for i :=1 to п do

then

нц для i от 1 до п

         если                   то

все

Как зависит итоговое значение переменной ј от значений массива А?

Ответ:

5.10.

а) Значения двумерного массива размера п х п задаются с помощью вложенного оператора цикла в представленном фрагменте программы:

 

Бейсик

Паскаль

Алгоритмический

FOR

FOR

IF

ELSE

END

NEXT К

NEXT п

ТО п ТО п

THEN

1

for i :=1 to п do for К: = 1 to п do if i>k then

A[i, k] :

нц для от 1 до п нц для К от 1 до п если i>k то

A[i, k] иначе

все

Как будет зависеть от п сумма элементов массива А после выполнения алгоритма? Напишите формулу вычисления суммы элементов массива А, в зависимости от п.

Ответ:

б) Значения двумерного массива размера п х п задаются с помощью вложенного оператора цикла в представленном фрагменте программы:

Бейсик

Паскаль

Алгоритмический

FOR                      ТО

FOR К=1 ТО

IF    THEN

ELSE

A(i, k)

END IF

NEXT К

NEXT п

п п

1

-1

for i:=1 to п do for К:=1 to п do if i=k then

e1se

для i от 1 до п для К от 1 до п если i=k то

иначе

все

кц кц

Как будет зависеть от п сумма элементов массива А после выполнения алгоритма? Напишите формулу вычисления суммы элементов массива А в зависимости от п.

Ответ:

в) Значения двумерного массива размера п х п задаются с помощью вложенного оператора цикла в представленном фрагменте программы:

 

 

Бейсик

Паскаль

Алгоритмический

FOR                  ТО п

FOR                  ТО п

IF THEN

   A (i, k)     1

ELSE

A(i, k)

END IF NEXT К

NEXT п

for i:=1 to п do for К:=1 to п do if• i>k then

A[i, k]

для •i от 1 до п для К от 1 до п если i>k то

иначе

все

кц кц

Как будет зависеть от п сумма элементов массива А после выполнения алгоритма? Напишите формулу вычисления суммы элементов массива А в зависимости от п.

Ответ:

г) Значения двумерного массива размера п х п задаются с помощью вложенного оператора цикла в представленном фрагменте программы:

 

Бейсик

Паскаль

Алгоритмический

FOR                ТО п

FOR К=1 ТО п

IF                 THEN

A(i, k)

ELSE

A(i, k)

END IF

NEXT К NEXT п

for i:=1 to п do for К: = 1 to п do if i>k then

нц для i от 1 до п для К от 1 до п если i>k то

иначе

все

кц кц

Как будет зависеть от п сумма элементов массива А после выполнения алгоритма? Напишите формулу вычисления суммы элементов массива А в зависимости от п.

Ответ:

5.11. Составить и записать в виде программы на любом языке программирования алгоритм, выполняющий:

                а)       решение уравнения alxl    Ь, где а и Ь — исходные числовые данные;

               б)       поиск количества минимальных элементов в заданном целочисленном массиве из

50 элементов;

поиск наибольшего общего делителя двух натуральных чисел;

        г)       поиск количества простых чисел в заданном целочисленном массиве из 50 элементов.

Важные рекомендации

Практика показывает, что наибольшие затруднения при выполнении заданий по теме «Алгоритмизация и программирование» вызывает составление программ и алгоритмов. Данное пособие не является учебником программирования, поэтому мы приведем лишь общие рекомендации, не зависящие от языка, на котором записываются программы:

*         Перед составлением программы надо тщательно проанализировать условие задания, уяснить постановку задачи, формат входных и выходных данных.

*         Приступать к написанию программы можно лишь тогда, когда детально продуман алгоритм решения задачи, не следует начинать писать программу, не представляя алгоритмического решения. Для простой задачи алгоритмическое решение можно держать и в голове, но лучше его зафиксировать на бумаге в виде пояснения или схемы.

*         Для написания программы нужно пользоваться тем языком программирования, которым хорошо владеешь и который подходит для решения поставленной задачи. Не следует специально стремиться поразить экзаменаторов знанием экзотического или недавно появившегося языка программирования, поскольку дополнительные баллы за это не предусмотрены. Хорошая программа должна быть максимально простой и эффективной. Не нужно специально использовать сложные приемы или редко применяемые конструкции языка программирования, если в этом нет необходимости.

*         Текст программы нужно писать аккуратно и разборчиво даже на черновике, структурированно, выделяя отступами уровень вложенности операторов, не скупясь на комментарии и пояснения. Отсутствие комментариев и пояснений вовсе не является признаком высокой квалификации программиста, скорее наоборот.

*         При написании текста программы следует контролировать соответствие типов переменных и применяемых к ним операций, не допускать использования неопределенных (неинициализированных) значений переменных.

*         Если текст программы получается, на ваш взгляд, очень сложным и запутанным, приостановите на время ее написание и подумайте, в чем причина этой сложности, нельзя ли найти более простое и изящное решение задачи.

*         После того как программа написана, необходимо выполнить ее тестирование, то есть проверку правильности работы для различных исходных данных. Постарайтесь найти ошибку в, своей программе, помните, что цель тестирования поиск ошибок, а не демонстрация правильности программы. Гораздо лучше, если ошибку найдете и исправите вы сами, а не экзаменаторы при проверке.

 При тестировании следует подбирать набор тестовых данных так, чтобы все операторы, все «ветки» программы выполнились на совокупности тестов. Особое внимание следует уделить особым случаям исходных данных, пограничным, критическим точкам. Пусть, например, написана программа сортировки массива. Особыми здесь будут случаи, когда входной массив уже отсортирован в нужном порядке, когда он отсортирован в порядке, обратном требуемому, а также когда все элементы сортируемого массива равны. Следует выявить такие критические точки и убедиться, что программа правильно работает на этих тестах.

 Если в задании приведен пример входных данных, его тоже надо включить в состав тестов, но он не должен быть единственным тестом!

*         При тестировании следует еще раз сверить структуру исходных и выходных данных с заданием, убедиться, что составленная программа точно соответствует условию задачи.  При тестировании необходимо внимательно контролировать синтаксис программы (должен быть явно указан тип каждой переменной, если этого требует язык программирования, переменные должны использоваться в соответствии со своим типом, не должно быть неинициализированных и неиспользуемых переменных, должны быть правильно расставлены операторные скобки и разделители операторов и т.д.).

 Если после тестирования программы осталось достаточно времени, то можно поработать над повышением ее эффективности, подумать, нельзя ли упростить ее, уменьшить количество циклов или требуемой для ее работы памяти. В случае внесения изменений в готовую программу процедуру тестирования придется повторить заново.

5.12.

а) Найдите и исправьте ошибки в приведенной программе проверки принадлежности точки закрашенной области. Приведите пример, когда исходная программа работала неправильно.

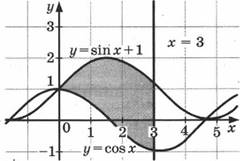
Программа на Паскале

Программа на Бейсике

Программа на Си

ar х, у: real; egin read1n (х, У) ; if y<=sin (х) 41 then if у>= cos (х) then if х<=З then write ( принадлежит '

rite ( ' не принадлежит ' nd.

INPUT х, У

IF (х) +1 THEN IF cos (х) THEN

IF х<=з THEN

PRINT принадлежит

ELSE

PRINT ” не принадлежит ” ENDIF

ENDIF

NDIF

oid main (void)

{ f10at х, у; scanf    , &х, &у) ; if         (х) +1) if (y>=cos (х) ) if (х<=З) printf ( ” принадлежит ” ) ;

rintf ( “ не принадлежит“) ;

       б)       Составьте программу проверки принадлежности точки закрашенной области.

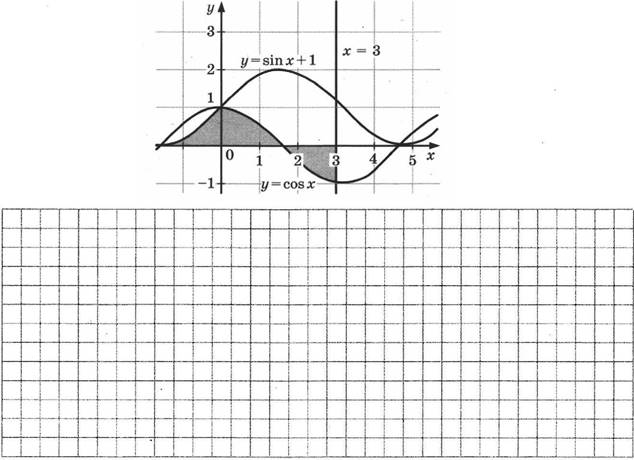
в) Найдите и исправьте ошибки в приведенной программе проверки принадлежности точки закрашенной области. Приведите пример, когда исходная программа работала неправильно.

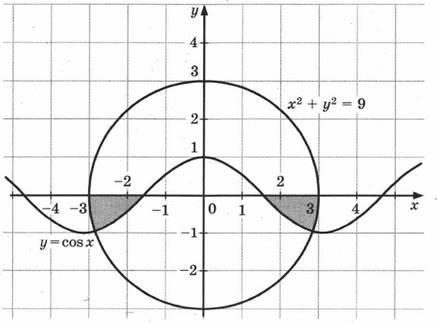
Программа на Паскале

var х, у: rea1; begin read1n (х, у) ; if (sqr (х) + sqr (у) ) or

write ( принадлежит ) e1se write ( не принадлежит ) end.

      ) then

Программа на Бейсике

INPUT х, У

IF (х * х + у * у <= 3) or

PRINT ” принадлежит ”

ELSE

PRINT “ не принадлежит ”

ENDIF

END

(х)  THEN

Программа на Си

void main (void)

{ f10at х, у; scanf if ( (х * х + у * у З) printf ( ” принадлежит ” ) ;

printf ( п не принадлежит )

(y>=cos (х)

              г)       Составьте программу проверки принадлежности точки закрашенной области.

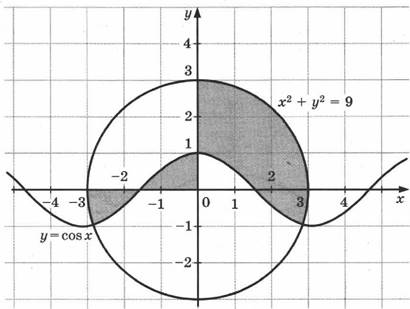
5.13.

а) Составить программу, выводящую на экран все натуральные трехзначные числа, делящиеся без остатка на 17, сумма цифр которых равняется 11.

6) Составить программу, выводящую на экран все натуральные трехзначные числа, делящиеся на 19 с остатком З, сумма цифр которых равняется 12.

в) На продовольственном складе имеется 10 ООО наименований различных продуктов, информация о которых хранится в текстовом файле. Каждому продукту отведена 1 строка файла. В ней указаны числовой артикул продукта, название (не содержащее пробелов), категория продукта (молочный, мясной или рыбный) и его стоимость. Вышеперечисленные поля разделены одним пробелом.

Написать программу, загружающую в память компьютера информацию о продуктах из текстового файла и выдающую на экран монитора наименования и артикулы всех рыбных продуктов, стоимость которых отличается от максимальной по данной категории не более чем на 10% .

г) На предприятии работает 1000 сотрудников, информация о которых хранится в текстовом файле. Каждому сотруднику отведена 1 строка файла. В ней указаны целочисленный индивидуальный табельный номер, фамилия сотрудника (не содержицая пробелов), стаж (целое число лет) и зарплата. Вышеперечисленные поля разделены одним пробелом.

Написать программу, загружающую в память компьютера информацию о сотрудниках из текстового файла и выдающую на экран фамилии и табельные номера всех сотрудников, проработавших не менее 8 лет, зарплата которых меньше средней зарплаты по предприятию более чем на 25% .

4

Задания в формате ЕГЭ

5.14.

        а)          Для составления цепочек используются бусины, помеченные буквами

Цепочка формируется по следующему правилу: в середине цепочки стоит одна из бусин 1, М, О. На третьем месте — бусина, помеченная любой гласной, если первая бусина — согласной, или любой согласной, если первая — гласной. На первом месте одна из бусин 1, О, Р, не стоящая в цепочке посередине.

Какая из перечисленных цепочек создана по этому правилу?

                    1) OPN                              2) P I I                              3) РОМ                             4) 1 1 0

б) Для составления цепочек используются бусины, помеченные буквами А, М, N, О, Р. Цепочка формируется по следующему правилу: в середине цепочки стоит одна из бусин М, О. На третьем месте бусина, помеченная любой гласной, если первая бусина — согласной, или любой согласной, если первая — гласной. На первом месте — одна из бусин N, О, Р, не стоящая в цепочке посередине.

Какая из перечисленных цепочек создана по этому правилу?

                    1) NMA                            2) NOM                            3) OON                             4) NAO

в) Для составления цепочек используются бусины, помеченные буквами А, Б, Г, Е, О. Цепочка формируется по следующему правилу: бусины с гласной и согласной буквой не могут стоять рядом. В середине цепочки может стоять одна из бусин Б или Е, не стоящая на первом месте. На третьем месте — бусина, помеченная любой гласной.

Какая из перечисленных цепочек создана по этому правилу?

                    1) АГЕ                              2) АЕА                              3) ГБА                              4) АБГ

г) Дешифровщику необходимо восстановить поврежденный фрагмент сообщения, состоящий из 4 символов. Имеется достоверная информация, что использовано не более пяти букв (А, Б, Е, В, Г), причем на втором месте стоит один из символов А, Г, Е, В. На первом — одна из букв Б, В, Г, Е, которой нет на третьем месте. На третьем месте одна из букв Е, А, Б, В, не стоящая в слове на втором месте. На четвертом месте — одна из букв А, Б, В, Г, которой не было на первом месте.

Появилась дополнительная информация, что возможен один из четырех вариантов.

Какой?

                    1) ЕВВА                            2) БЕБА                           3) ВВАА                           4) ГЕАГ

Рассмотрим пример решения задачи на работу с последовательностями символов. Пример. Записано 9 строк, каждая имеет свой номер — от 1 до 10.

В первой строке записана цифра 1.

Каждая последующая строка состоит из двух повторений предыдущей и добавленного в конец своего номера (в Ј-й строке в конце приписана цифра i).

Ниже показаны первые четыре строки, сформированные по описанному правилу (в скобках записан номер строки):

(2)   112

(3)   1121123    (4) 112112311211234

Какая цифра стоит в 9-й строке на 510-м месте (считая слева направо)?

Решение.

Сначала вычислим длину 9-й строки.

Заметим, что длина каждой строки равна удвоенной длине предыдущей плюс один символ. Составим таблицу:

N2 строки

1

2

з

4

5

6

7

8

9

Длина

1

з

7

15

31

63

127

255

511

Примечание: можно доказать (например, по индукции), что длина ј-й строки будет равна 2' — 1. Итак, 510-й символ будет предпоследним в 9-й строке. Заметим также, что каждая строка завершается последовательностью 1 ... п, где п — номер строки.

Таким образом, 9-я строка будет заканчиваться на 123456789, а ее предпоследним (510-м) символом будет 8.

5.15. Записано 7 строк, каждая имеет свой номер — от 1 до 7.

В первой строке записана цифра 1.

Каждая последующая строка состоит из двух повторений предыдущей и добавленного в конец своего номера (в Ј-й строке в конце приписана цифра i). Ниже показаны первые четыре строки, сформированные по описанному правилу (в скобках записан номер строки):

(2)  112

(3)  1121123

(4)  112112311211234

        а)        Какая цифра стоит в 7-й строке на 66-м месте (считая слева направо)?

б) Запишите в ответе последовательность цифр, стоящих в 7-й строке с 123-й по 125-ю позиции (считая слева направо).

в) Запишите в ответе последовательность цифр, стоящих в 8-й строке с 15-й по 17-ю позицию (считая слева направо).

позицию (считая слева направо).

5.16. Строки (цепочки символов латинских букв) создаются по следующему правилу.

Первая строка состоит из одного символа — латинской буквы «А». Каждая из последующих цепочек создается такими действиями: в очередную строку сначала записывается буква, чей порядковый номер в алфавите соответствует номеру строки (на i-M шаге пишется «Ј»-я буква алфавита), к ней справа дважды подряд приписывается предыдущая строка.

Вот первые 4 строки, созданные по этому правилу:

(2)  ВАА

(3)  СВААВАА      (4) DCBAABAACBAABAA

Латийский алфавит (Для справки): ABCDEFGHIJKLMNOPQRSTUVWXYZ

а) Запишите четыре символа подряд, стоящие в 7-й строке с 6-го по 9-е место (считая слева направо).

б) Запишите три символа подряд, стоящие в 8-й строке с 253-го по 255-е место (считая слева направо).

5.17.

              а)       У исполнителя Утроитель две команды, которым присвоены номера:

1. Вычти 1

2. Умножь на З

Первая из них уменьшает число на экране на 1, вторая — увеличивает его в три раза. Запишите порядок команд в программе получения из числа 5 числа 34 для данного исполнителя, содержащей не более 5 команд, указывая лишь номера команд. Например, программа 21211 — это программа: умножь на З вычти 1 умножь на З вычти 1 вычти 1 которая преобразует число 1 в 4.

Ответ:

б) Запишите порядок команд в программе получения из числа 4 числа 31 для исполнителя Утроитель, содержащей не более 5 команд, указывая лишь номера команд.

Ответ:

             в)       У исполнителя Квадратор две команды, которым присвоены номера:

1.  Прибавь 1

2.  Возведи в квадрат

Первая из них увеличивает число на экране на 1, вторая — возводит его в квадрат. Запишите порядок команд в программе получения из числа 6 числа 66 для исполнителя Квадратор, содержащей не более 5 команд, указывая лишь номера команд.

Ответ:

г) Запишите порядок команд в программе получения из числа 2 числа 50 для исполнителя Квадратор, содержащей не более 6 команд, указывая лишь номера команд.

Ответ:

Система команд исполнителя РОБОТ, клетчатой плоскости:

«живущего» в прямоугольном лабиринте на

вверх

вниз

 

влево

вправо

5.18.

При выполнении этой команды РОБОТ перемещается на соответствующую клетку. Команды проверки истинности условия на наличие стены у той клетки, где он находится:

сверху свободно

снизу свободно

слева свободно

справа свободно

Если РОБОТ начнет движение в сторону стены, то он разрушится.

а) Сколько клеток данного лабиринта соответствует требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?

НАЧАЛО

8

ПОКА справа свободно7

ДЕЛАТЬ вправо

6

ПОКА снизу свободно

5

ДЕЛАТЬ вниз4

ПОКА слева свободноз

ДЕЛАТЬ влево2

ПОКА сверху свободно1

ДЕЛАТЬ вверх КОНЕЦ

В ответе запишите число количество таких клеток, а далее, через запятые, их адреса (сначала идет латинская буква столбца, а затем цифра строки). Например, нижний левый угол лабиринта имеет адрес А 1.

Ответ:

6) Сколько клеток данного лабиринта соответствует требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?

НАЧАЛО

8

ПОКА сверху свободно7

ДЕЛАТЬ вверх 6

ПОКА слева свободно

5

ДЕЛАТЬ влево4

ПОКА снизу свободноз

ДЕЛАТЬ вниз2

ПОКА справа свободно1

             ДЕЛАТЬ вправо                      A B C D E F G H

КОНЕЦ

В ответе запишите число — количество таких клеток, а далее, через запятые, их адреса (сначала идет латинская буква столбца, а затем цифра строки). Например, нижний левый угол лабиринта имеет адрес А1.

Ответ:

в) Сколько клеток данного лабиринта соответствует требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?

НАЧАЛО

ПОКА сверху свободно

ДЕЛАТЬ вверх

ПОКА слева свободно ДЕЛАТЬ влево

ПОКА снизу свободно

ДЕЛАТЬ вниз

ПОКА справа свободно

ДЕЛАТЬ вправо

КОНЕЦ

В ответе запишите число — количество таких клеток, а далее, через запятые, их адреса (сначала идет латинская буква столбца, а затем цифра строки). Например, нижний левый угол лабиринта имеет адрес А 1.

Ответ:

г) Сколько клеток данного лабиринта соответствует требованию, что, выполнив предложенную программу, РОБОТ остановится в той же клетке, с которой он начал движение?

НАЧАЛО8

ПОКА справа свободно7

ДЕЛАТЬ вправо6

ПОКА сверху свободно5

ДЕЛАТЬ вверх4

ПОКА слева свободноз

ДЕЛАТЬ влево2

ПОКА снизу свободно1

ДЕЛАТЬ вниз   A B C D E F G H КОНЕЦ

Ответ:

5.19. Определите значение переменной с после выполнения фрагмента алгоритма:

а)

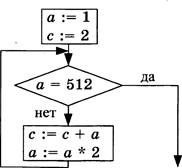
Примечание: знаком обозначена операция присваивания. знаком * обозначена опреация умножения

Ответ:

6)

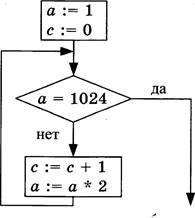
               Ответ:

              в)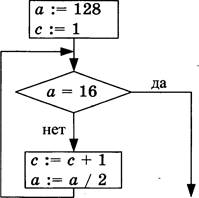                                                               

Ответ: г)    

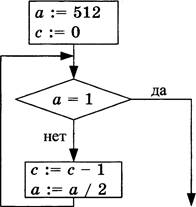
Ответ:

5.20. Определите значение целочисленных переменных а и Ь после выполнения фрагмента программы:

Бейсик

Паскаль

Алгоритмический

а=З+2 * 4

MOD 10) +24

'\ и MOD — операции, вычисляющие результат деления нацело первого аргумента на второй и остаток от деления соответственно

а : = 3+2 * 4;

Ь: = (а mod 10) +24; а : = (Ь div 10) +1

{div и mod — операции, вычисляющие результат деления нацело первого аргумента на второй и остаток от деления соответственно}

а : = 3+2 * 4

Ь: =mod (а, 10) +24

(Ь, 10) +1

Biv и mod — функции, вычисляющие результат деления нацело первого аргумента на второй и остаток от деления соответственны

а)

Бейсик

Паскаль

Алгоритмический

а = (3+2) * 4

MOD 5) +11

а : = (3+2) * 4;

Ь: — (а mod 5) +11; а : = (Ь div З) +1

а : = (3+2) * 4 Ь : =mod (а, 5) +11 a:=div(b, З) +1

- З, Ь = 24         2) а - З, Ь - 25Ь - 25    4) а 4,             35 б)

                       4, ь = 11           2)     - 4,                 12- 11                      - 15

Бейсик

Паскаль

Алгоритмический

а=(З—2) * 4

MOD 5) +12

(а mod 5) +12; div З) +1

а : = (3—2) * 4

Ь : =mod (а, 5) +12

в)

Бейсик

Паскаль

Алгоритмический

MOD 6) +12

а:= 24 — 4; mod 6) +12; div

Ь: =mod (а, 6) +12 a:=div (Ь, 7) +1

- 2, ь = 12          2) а - 2, Ь - 16          З, ь - 12         16 г)

                      - 2, Ь - 22                2)        - 4, Ь - 22                            З,         16               4) 0 = 6, ь = 16

5.21.

       а)       Дан фрагмент программы, обрабатывающей массив А из п элементов:

 

Бейсик

 

Паскаль

Алгоритмический

FOR

NEXT i

то п

< А(ј) THEN Ј

i

for i :=1 to п do begin if A[i] [ј ] then end

нц для i от 1 до п если A[i]    22

все

Чему будет равно значение переменной s после выполнения данного алгоритма при любых значениях элементод массива А?

1)    Индексу минимального элемента в массиве А (первому из них, если минимальных элементов несколько)

2)    Индексу минимального элемента в массиве А (последнему из них, если минимальных элементов несколько)

З) Индексу максимального элемента в массиве А (последнему из них, если максимальных элементов несколько)

4) Индексу максимального элемента в массиве А (последнему из них, если максимальных элементов несколько)

       б)       Дан фрагмент программы, обрабатывающей массив А из п элементов:

Бейсик

 

Паскаль

 

Алгоритмический

Ј               1

1 то п

А(ј) THEN

NEXT i

i

for i :=1 to п do begin if A[i] [ј ] then

з .

для i от 1 до п

         если то

все кц

Чему будет равно значение переменной s после выполнения данного алгоритма при любых значениях элементов массива А?

1)     Индексу элемента, равного первому и имеющему наибольший индекс

2)     Индексу элемента, равного последнему и имеющему наименьший индекс

З) Значению п

4) Единице

               в)       Дан фрагмент программы, обрабатывающей двумерный массив А размера п х п.

Бейсик

Паскаль

Алгоритмический

К          1

FOR i        1 то п с    A (i, К+2)

NEXT i

for i :=1 to п do begin end

нц для i от 1 до п

A[i, k] :=с кц

Представим массив в виде квадратной таблицы, в которой для элемента массива A[i, ј] величина i является номером строки, а величина ј — номером столбца, в котором расположен элемент. Тогда данный алгоритм меняет местами:

1)    два столбца в таблице

2)    две строки в таблице

З) элементы диагонали и К-й строки таблицы

4) элементы диагонали и К-го столбца таблицы

               г)       Дан фрагмент программы, обрабатывающей двумерный массив А размера п х п.

Бейсик

Паскаль

Алгоритмический

К          з

FOR i      1 то п с      A (i, i)

NEXT i

for i :=1 to п do begin

нц для i от 1 до п

A [i, i] :=A[i, k]

A[i, k] :=с кц

Представим массив в виде квадратной таблицы, в которой для элемента массива A[i, ј] величина i является номером строки, а величина ј — номером столбца, в котором расположен элемент. Тогда данный алгоритм меняет местами:

1)    два столбца в таблице

2)    две строки в таблице

З) элементы диагонали и К-й строки таблицы

4) элементы диагонали и К-го столбца таблицы

5.22. Составить и записать в виде программы на любом языке программирования или в виде блок-схемы или на естественном языке алгоритм, выполняющий:

а) поиск минимального нечетного элемента в заданном целочисленном массиве из 50 элементов. Известно, что в массиве есть хотя бы один нечетный элемент;

4.

1.

б) поиск среднего арифметического четных элементов в заданном целочисленном массиве из 50 элементов. Известно, что в массиве есть хотя бы один четный элемент;

4.

noncK pa3Hocrrn MaKCMMU1bHO qeTHoro MHHHMU1bHO HeqeTHoro e.J1er.aeHTOB B gamaHHOM 1.xeJIOt1HC.neHHOM MaccnBe H3 50 3J1eMeHTOB. V13BeCTHO, t1T0 B MaCCHBe eCTb qeTHb1e, HeqeT1--1b1e OJIeMeHTb1',

                                                                                                                                        I .1                                                                                                                              .1.-

4.

 поиск второго после максимального по величине элемента в заданном целочисленном массиве из 50 различных элементов.

5.23.

а) Требовалось написать программу, которая решает неравенство «ах — Ь < О» относительно х для любых чисел а и Ь, введенных с клавиатуры. Все числа считаются действительными. Программист торопился и написал программу неправильно.

П о амма на Паскале

П ог амма на Бейсике

П ог амма на Си

var а, Ь, х: rea1; begin readln (а, Ь) ; if а 0 then write ( ' любое число '

if а < 0 then write ( Ix   ,b/a)

write ( '  b/a) ; end.

INPUT

PRINT

ELSE

PRINT

ELSE PRINT

END

а, Ь

О THEN “ любое число ”

THEN

>” ,b/a

<” ,b/a

void main (void)

{ f10at а, Ь, х; scanf (”%f%f" ,

printf ( “ любое число

if (а<0) printf ,b/a) ;

printf (”x<%f” ,b/a) ;

Последовательно выполните два задания:

1)    приведите пример таких чисел а, Ь, х, при которых программа неверно решает поставленную задачу;

2)    укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы.)


б) Требовалось написать программу, которая решает уравнение «ах = Ь» относительно х для любых чисел а и Ь, введенных с клавиатуры. Все числа считаются действительными. Программист торопился и написал программу неправильно.

 

П о амма на Паскале

П ог амма на Бейсике

П о амма -на Си

var а, Ь: rea1; begin readln (а, Ь) if Ь — 0 then write ( 'x

if а — 0 then write ( нет решений '

write ( t x   ,b/a) ;

INPUT

- О THEN

PRINT

ELSE

 О THEN

PRINT “нет решений ”

ELSE

PRINT                ,b/a

END

void main (void) { f10at а, Ь;

printf (”x=O”) ;

if (а==0) printf (”нет решений“) ; e1se printf ,b/a) ;

Последовательно выполните два задания:

1)   приведите пример таких чисел а, Ь, х, при которых программа работает неправильно;

2)   укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому моэкно указать любой способ доработки исходной программы.)

в)Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у — действительные числа) и определяет принадлежность точки закрашенной области, включая ее границы. Программист торопился и написал программу неправильно.

Программа на Паскале

Программа на Бейсике

Программа на Си

ar х, у: rea1; egin readln (х, у) ; if y>=sqr (х) then if у<=б—х then write ( принадлежит

rite ( не принадлежутт nd.

INPUT х, У

IF                      * х ТНЕН

IF          6-х THEN

PRINT принадлежит

ELSE

PRINT ” не принадлежат ” ENDIF

ENDIF

oid main (void)

{ f10at х, у; scanf  , &х, &у) ; if (у>=х * х)

printf ( ” принадлежит“ ) ;

rintf ( ” не принадлежит“ ) ;

Последовательно выполните следующее:

1)   приведите пример таких чисел х, у, при которых программа работает неправильно;

2)   укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы.)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

-4=3 -2-1

 

 

 

г)Требовалось написать программу, которая

вводит с клавиатуры координаты точки на плоскости (х, у — действительные числа) и определяет принадлежность точки закрашенной области, включая ее границы. Программист торопился и написал программу неправильно.

Программа на Паскале

Программа на Бейсике

Программа на Си

var х, у: real; begin read1n (х, у) ; if y<=6—sqr (х) then if у>=—х then write ( принадлежит '

write ( ' не принадлежит ' ) end.

INPUT х, У

* х ТНЕђ4

6—х THEN

PRINT ” принадлежит ”

ELSE

PRINT п не принадлежат ”

ENDIF

ENDIF

END

void main (void)

{ f10at х, у; scanf  &у) • if (у<=б—х * х) if                       printf ( ” принадлежит ”) ;

printf (” не принадлежит ”) ;

Последовательно выполните следующее:

1)   приведите пример таких чисел х, у, при которых программа работает неправильно;

2)   укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы.)

5.24.

а)Требовалось написать программу, которая вводит с

клавиатуры координаты точки на плоскости (х, у — действительные числа) и определяет принадлежность точки закрашенной области, включая ее границы. Программист торопился и написал программу неправильно.

 

Программа на Паскале

Программа на Бейсике

Программа на Си

ar х, у: rea1; egin read1n (х, у) ; if         then if         then then if у>=х*х then write ( принадлеит )

rite ( ' не ' )

INPUT х, У

2-х THEN

THEN

PRINT ” принадлежит

ELSE

PRINT ”не принадлежит ”

ENDIF

ENDIF

ND

oid main (void)

{ f10at х, у;

, &х, &у) ;

if (у>=х*х) printf ( ” принадлежит ” ) ;

rintf ( П не принадлежит ”) ;

Последовательно выполните следующее:

1)   перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах, принадлежащих различным областям (А, В, С, D, Е, Р, G, Н, и Ј). Границы принадлежат заштрихованным областям (F и G).

Область

Условие 1

Условие 2

Условие З

Условие 4

(            х*х)

Программа выведет

Область обрабатывается ве но

 

 

 

 

 

 

 

в

 

 

 

 

 

 

с

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

н

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В столбцах условий укажите «Да», если условие выполнится, «Нет», если условие не выполнится, «—» (прочерк), если условие не будет проверяться, «Не изв.», если программа ведет себя по-разному для разных значений, принадлежащих данной области. В столбце «Программа выведет» укажите, что программа выведет на экран. Если программа ничего не выводит, напишите «—» (прочерк). Если для разных значений, принадлежащих области, будут выведены разные тексты, напишите «Не изв.». В последнем столбце укажите «Да» или «Нет»;

2)   укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому моэкно указать любой способ доработки исходной программы.)

б)Требовалось написать программу, при выполнении ко-

торой с клавиатуры считывается координата точки на прямой (х действительное число) и определяется принадлежность этой точки одному из выделенных отрезков В и D (включая границы). Программист торопился и написал программу неправильно.

Программа на Паскале

Программа на Бейсике

Программа на Си

ar х; rea1; egin read1n (х) ; if х>=—2 then if х<=7 then if then write ( принадлежит )

rite ( ' не принадлежит ' ) nd.

INPUT х

IF х - —2 THEN 7 THEN

4 ТНЕН

PRINT ” принадлежит “

ELSE

PRINT ” не принадлежит ” ENDIF

ENDIF

oid main (void)

{ f10at х; scanf C'%f” , &х) ; if (х>=—2) if (х<=7) if (х<4) printf ( ” принадлежит“ ) ;

rintf ( “не принадлежит") ;

Последовательно выполните следующее:

1)   перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах, принадлежащих различным областям (А, В, С, D и Е). Границы (точки 2, 1, 4 и 7) принадлежат заштрихованным областям (В и D соответственно).

Область

Условие 1

Условие 2

Условие З

Программа выведет

Область обрабатывается верно

 

 

 

 

 

 

в

 

 

 

 

 

с

 

 

 

 

 

D

 

 

 

 

 

 

 

 

 

 

 

В столбцах условий укажите «Да», если условие выполнится, «Нет», если условие не выполнится, «—» (прочерк), если условие не будет проверяться, «Не изв.», если программа ведет себя по-разному для разных значений, принадлежащих данной области. В столбце «Программа выведет» укажите, что программа выведет на экран. Если. программа ничего не выводит, напишите «—» (прочерк). Если для разных значений, принадлежащих области, будут выведены разные тексты, напишите «Не изв.». В последнем столбце укажите «Да» или «Нет»;

2)   укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы.)

в)Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у — действительные числа) и определяет принадлежность точки закрашенной области, включая ее границы. Программист торопился и написал программу неправильно.

Программа на Паскале

Программа на Бейсике

Программа на Си

ar х, у: rea1; egin readln (х, у) ; if х*х+у*у<=1 then if у<=х then if у >=—х then write ( принадлежит ' )

rite ( ' не принадлежат )

INPUT х, У

IF 1 THEN

TF у            х THEN

-х THEN PRINT ” принадлежит “

ELSE

PRINT           принадлежит”

ENDIF

ENDIF

END

0id main (void)

{ float х, у;

,       &у) ; if

      (У<=х) if (У>=—х) printf ( ” принадлежит ” ) ; e1se rintf (    принадлежит ”) ;

Последовательно выполните следующее:

1)     перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах, принадлеэкащих различным областям (А, В, С, D, Е, Р, G и Н). Границы принадлежат заштрихованным областям (Р, G

Область

Условие 1

Условие 2

Условие 4

Программа выведет

Область обрабатывается ве но

 

 

 

 

 

 

в

 

 

 

 

 

С

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

н

 

 

 

 

 

В столбцах условий укажите «Да», если условие выполнится, «Нет», если условие не выполнится, «—» (прочерк), если условие не будет проверяться, «Не изв.», если программа ведет себя по-разному для разных значений, принадлежащих данной области. В столбце «Программа выведет» укажите, что программа выведет на экран. Если программа ничего не выводит, напишите «—» (прочерк). Если для разных значений, при надлежащих области, будут выведены разные тексты, напишите «Не изв.». В последнем столбце укажите «Да» или «Нет»;

2)     укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы.)

г)Требовалось написать программу, при выполнении которой с клавиатуры считывается координата точки на пря-2 мой (х — действительное число) и определяется принад-

лежность этой точки одному из выделенных отрезков В и D (включая границы). Программист торопился и написал программу неправильно.

Программа на Паскале

Программа на Бейсике

Программа на Си

ar х: rea1; egin read1n (х) ; if х<=10 then if х>=—2 then if      then write ( ' принадпе;юат ' e1se rite ( ' не принадпежат end.

INPUT х

IF х                  10 THEN

IF х        -2 THEN

        IF х                6 THEN

PRINT “ принадлежит ”

ELSE

PRINT  п не принадлежит“

ENDIF

ENDIF

void main (void) { f10at х;

&х) ; if if

printf ( ” принадлежит” ) ; e1se rintf ( И не принадлежит”) ;

Последовательно выполните следующее:

1)   перерисуйте и заполните таблицу, которая показывает, как работает программа при аргументах, принадлежащих различным областям (А, В, С, D и Е). Границы (точки —2, 2, 6 и 10) принадлежат заштрихованным областям (В и D соответственно).

Область

Условие 1

= 10)

Условие 2

Условие З

Программа выведет

Область обрабатывается ве но

 

 

 

 

 

 

в

 

 

 

 

 

с

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В столбцах условий укажите «Да», если условие выполнится, «Нет», если условие не выполнится, «—» (прочерк), если условие не будет проверяться, «Не изв.», если программа ведет себя по-разному для разных значений, принадлежащих данной области. В столбце «Программа выведет» укажите, что программа выведет на экран. Если программа ничего не выводит, напишите «—» (прочерк). Если для разных значений, принадлежащих области, будут выведены разные тексты, напишите «Не изв.». В последнем столбце укажите «Да» или «Нет»;

2)   укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы.)

5.25.

а) сведения о сотрудниках некоторой организации. В первой строке сообщается количество сотрудников N, которое не меньше 5, но не превосходит 1000, каждая из следующих N строк имеет следующий формат: <Фамилия> <Должность> <Стаж> <Оклад> <Премия>, где

              <Фамилия>      строка, состоящая не более чем из 20 символов;

              <Должность>      строка, состоящая не более чем из 15 символов;

<Стаж> <Оклад> <Премия> — целые числа. Под стажем понимается количество полных лет, отработанных сотрудником в данной организации. Оклад и премия — целые числа, не превышающие 1 ООО ООО.

Эти элементы входной строки отделены друг от друга одним пробелом. Пример входной строки:

Иванов механик 15 25500 5000

Требуется написать программу (укажите язык программирования, который вы используете), которая будет выводить на экран фамилии, должности и стаж трех сотрудников с наибольшей зарплатой. Если среди остальных есть сотрудники с такой же зарплатой, что и один из этих трех, то следует также вывести и их фамилии, должности и стаж. Зарплата сотрудника равна сумме его оклада и премии.

—4...4—4

б) сведения о сотрудниках некоторой организации. В первой строке сообщается количество сотрудников N, которое не меньше 5, но не превосходит 1000, каждая из следующих N строк имеет следующий формат: <Фамилия> <Должность> <Стаж> <Оклад> <Премия>, где

<Фамилия> — строка, состоящая не более чем из 20 символов;

<Должность> — строка, состоящая не более чем из 15 символов;

<Стаж> <Оклад> <Премия> — целые числа. Под стажем понимается количество полных лет, отработанных сотрудником в данной организации. Оклад и премия — целые числа, не превышающие 1 ООО ООО.

Эти элементы входной строки отделены друг от друга одним пробелом. Пример входной строки:

Иванов механик 15 25500 5000

Требуется написать программу (укажите язык программирования, который вы используете), подсчитывающую среднюю зарплату сотрудников, стаж которых больше среднего по организации.

Зарплата сотрудника равна сумме его оклада и премии.

„„т

в) строчные английские буквы. Ввод этих символов заканчивается точкой (другие символы, отличные от «.» и букв «а» ... «z», во входных данных отсутствуют; в программе на языке Бейсик символы можно вводить по одному в строке, пока не будет введена точка).

Требуется написать эффективную программу (укажите язык программирования, который вы используете), которая будет печатать в алфавитном порядке только те буквы, которые ровно три раза подряд встретились во входной последовательности. Каждая буква должна быть распечатана только один раз. Точка при этом не учитывается.

Например, пусть на вход подаются следующие символы: btfgbbffjrtatbama.

В данном случае программа должна вывести: Aft

„1

г) строчные английские буквы. Ввод этих символов заканчивается точкой (другие символы, отличные от «.» и букв «а» ... «z», во входных данных отсутствуют; в программе на языке Бейсик символы можно вводить по одному в строке, пока не будет введена точка).

Требуется написать эффективную программу (укажите язык программирования, который вы используете), которая будет печатать в алфавитном порядке только те буквы, которые хотя бы однократно ровно три раза подряд встретились во входной последовательности. Каждая буква должна быть распечатана только один раз. Точка при этом не учитывается.

Например, пусть на вход подаются следующие символы: bbbffjrtatbbbamaaa. В данном случае программа должна вывести: ab

5.26. Алгоритм вычисления значения функции F(n), где п — натуральное число, задан сле- дующими соотношениями:

F(n) = F(n—1) + F(n/2), при п>1 и п кратно 2

F(n) = F(n—1) + 1, при п>1 и п не кратно 2 1

Чему равно значение функции F(8)?

Рекомендация. Будем вычислять значение функции последовательно, начиная от 1:

1 (дано по условию)

1 + 1 = 2. (2 кратно 2, по формуле F(n) = F(n-1) + F(n/2) = F(2-1) + F(2/2).

+ F(4/2) = ЯЗ) + F(2) = З + 2 = 5.

5.27. Алгоритм вычисления значения функции F(n), где п дующими соотношениями:

F(n) = F(n—1) + F(n/2), при п>1 и п кратно 2

F(n) = F(n—1) + F(n—2), при п>1 и п не кратно 2      1

Чему равно значение функции F(8)?

натуральное число, задан сле-

5.28. Алгоритм вычисления значения функции F(h), где п

натуральное число, задан сле-

дующими соотношениями:

F(n) = 2*F(n/2), при- п>2 и п кратно 2

F(n) = F(n—1) + 2*F(n—2), при и п не кратно 2 F(n) = п, при п<З

Чему равно значение функции F(9)?

5.29. Требовалось написать программу, при выполнении которой с клавиатуры считывается натуральное число N (N<109) и выводится на экран максимальная цифра этого числа. Программист торопился и написал программу неправильно.

Программа на Паскале

Программа на Бейсике

Программа на Си

ar N, k: integer; egin read1n (N) ;

while N    10 do begin if N mod 10>k then k:=N mod 10;

N:=N div 10 end; write (К) end.

INPUT N

НПЕ N           10

IF N MOD 10 > к THEN

MOD 10

ENDIF

10

END

PRINT К

oid main (void)

{ int N, k; scanf ( 'I %d” , &N) ; К  9; while (N >= 10) if (N % 10 > К)

rintf ( 't %d” , К) ;

Выполните следующие действия:

1.  Напишите, что выведет программа при вводе числа 537.

2.  Приведите пример такого числа, при котором программа работает верно.

З. Укажите все ошибки в программе и исправьте их. Для этого для каждой ошибки: выпишите строку, которая написана неправильно и приведите правильный вариант строки.

Рекомендация. для ответа на первый вопрос настоятельно рекомендуем выполнить трассировку предложенного алгоритма для указанного числа. Важно при этом не принимать желаемое за действительное и выполнять именно то, что делает алгоритм, а не то, что он должен бы, вроде бы, в этот момент делать.

Для трассировки нужно составить таблицу, в которой столько же столбцов, сколько переменных описано в программе и, «водя пальцем» по строчкам программы, от начала, последовательно, в порядке выполнения, для каждой строчки менять значение той переменной в ее столбце таблицы, которая этой строчкой программы меняется.

Обычно используют краткую трассировку, для убыстрения. Мы приведем полную таблицу трассировки (в ней мы будем указывать еще и выполняемую в данный момент строюу на языке Паскаль), чтобы процесс был наиболее понятен.

 

 

Опе ато

Условие

537

 

read1n (N) ;

 

 

9

 

 

 

 

whi1e N>=10 do

 да

 

 

if N mod 10>k then

7>9, нет

53

 

div 10

 

 

 

whi1e N>=10 do

 да

 

 

if N mod 10>k then

3>9, Нет

5

 

div 10

 

 

 

whi1e N>=10 do

Нет

 

 

write (К)

На экране: 9

Эта трассировка, кроме ответа на первый вопрос (9), должна нам подсказать, где программа работает неправильно.

Конечно, для решения этой задачи очень желательно уметь самому составлять такой алгоритм. Эта задача относится к одному из вариантов перевода числа в некоторую систему счисления (основанием не больше 10). В данном случае в десятичную систему счисления. А именно: из числа последовательно извлекается младшая цифра (нахождением остатка от деления на 10), после чего эта цифра из числа вычеркивается (целочисленным делением на 10). Потом процесс повторяется, пока в числе не окажется цифр.

Анализируя работу программы, обнаруживаем, что переменная К в процессе работы не менялась. Ни одна из цифр числа N не оказывается меньше 9. Отсюда находим первую ошибку — начальное значение К нужно было сделать не наибольшим из возможных (9, как сейчас), а, наоборот, наименьшим. То есть, нулем.

Получается, что число К при любом N не будет меняться и программа всегда будет выдавать 9. Значит, для ответа на второй вопрос (при каком числе программа будет работать верно) достаточно указать любое число, в котором наибольшая цифра и есть 9. Например, просто число 9.

Поищем еще ошибки. Если Вы внимательно выполняли задание 2.16, то, возможно, обратили внимание на то, что процесс деления на 10 нужно продолжать, пока исходное число не станет равным нулю.

А в процессе трассировки Вы, скорее всего, заметили, что старшая (первая) цифра числа N (в данном случае 5) вообще не сравнивалась с переменной К. Задаемся вопросом, почему, и находим противоречие с тем, как программа должна была работать. Вместо того, чтобы делить число N на 10, пока оно не станет равно 0, приведенная программа останавливается, как только число N становится меньше 10. Значит, вторая ошибка — неверное условие окончания цикла «while».

Нужно было остановиться, когда число N станет равно нулю. Значит, условие продолжения цикла — пока число N не равно нулю (так как нам известно, что исходное число N натуральное, достаточно написать, что N больше нуля).

Общий план решения задачи:

1.       Выполните аккуратно трассировку для предложенного числа.

2.       Постарайтесь понять, что в программе помешало получить правильный ответ.

з. Исправьте строку, в которой Вы обнаружили ошибку, и снова выполните трассировку для предложенного числа. Возможно, Вы при этом обнаружите еще одну ошибку.

4.       Если в условии имеется пункт, предлагающий подобрать число, при котором программа работает верно, постарайтесь подобрать такое число. Возможно, подойдет такое число, которое удовлетворяет начальному значению искомой величины (если ошибка в начальном значении, как в этом примере). Либо подберите число, при котором цикл выполняется нужное количество раз (если ошибка — в условии окончания цикла). В любом случае, еще раз выполните трассировку для подобранного числа и убедитесь, что программа действительно выдает нужный ответ.

5.       Аккуратно выпишите те строки, которые содержат ошибку, и приведите правильные варианты этих строк.

5.30.   Требовалось написать программу, при выполнении которой с клавиатуры считывается натуральное число N (N<10[6] ) и выводится на экран минимальная цифра этого числа. Программист торопился и написал программу неправильно.

Программа на Паскале

Программа на Бейсике

Программа на Си

ar N, k: integer; egin read1n (N) ;

whi1e N > 9 do begin if N mod 10<k then k:=N mod 10;

N:=N div 10 end; write (К) end.

INPUT N

HILE N > 9

IF N MOD 10 < к THEN

MOD 10

ENDIF

                  10

END

PRINT К

oid main (void)

{ int N, k; scanf (”%d” , &N) ;

К whi1e (N > 9)

10 < К)

          к                 

rintf ("%d” , К) ;

Выполните следующие действия:

1.  Напишите, что выведет программа при вводе числа 357.

2.  Приведите пример такого числа, при котором программа работает верно.

З. Укажите все ошибки в программе и исправьте их. Для этого для каждой ошибки: выпишите строку, которая написана неправильно и приведите правильный вариант строки.

5.31.   Требовалось написать программу, при выполнении которой с клавиатуры считывается

Программа на Паскале

Программа на Бейсике

Программа на Си

ar N, k: integer; egin read1n (N) ; k:=N mod 10; whi1e N > 1 do begin

k:=k+N mod 10; div 10 end; write (К) end.

INPUT N

MOD 10 HILE N > 1 k=k+N MOD 10

10

END

PRINT К

oid main (void)

{ int N, k; scanf , &N) ;

whi1e (N > 1)

       К                        

N / 10;

rintf (”%d” , К) ;

Выполните следующие действия:

1.  Напишите, что выведет программа при вводе числа 357.

2.  Приведите пример такого числа, при котором программа работает верно.

З. Укажите все ошибки в программе и исправьте их. Для этого для каждой ошибки: выпишите строку, которая написана неправильно и приведите правильный вариант строки.

5.32.   Требовалось написать программу, при выполнении которой с клавиатуры считывается натуральное число N (N<109) и выводится на экран произведение цифр этого числа. Программист торопился и написал программу неправильно.

Программа на Паскале

Программа на Бейсике

Программа на Си

ar N, k:integer;

read1n (N) ;

whi1e N > 0 do begin k:=k*N mod 10;

N:=N div 10 end; write (К)

INPUT N

HILE N > О MOD 10 10

END

PRINT К

oid main (void)

{ int N, k; scanf         &N) • К        о; whi1e (N > 0)

       к                            

N / 10;

rintf        , К) ;

Выполните следующие действия:

                1, Напишите, что выведет программа при вводе числа 257.

2. Приведите пример такого числа, при котором программа работает верно.

З. Укажите все ошибки в программе и исправьте их. Для этого для каждой ошибки:

выпишите строку, которая написана неправильно и приведите правильный вариант строки.

5.33.   У исполнителя Удвоитель две команды, которым присвоены номера:

1.  Прибавь 1,

2.  Умножь на 2.

Первая из них увеличивает число на экране на 1, вторая увеличивает число на экране вдвое. Программа для Удвоителя — это последовательность команд. Сколько есть программ, которые число 1 преобразуют в число 21?

Peuenue.

ByzxeM 110CJ1eAOBarreJ1bHO BblHHCJIHTb KOJInqeCTBO nporpaMM (F(N)), I-co rropble qncno 2 npe06pa3YK)T B I-IHCJIO N. AJ1fl 3Toro 6YÅervf gallOJIHflTb era6J1uuy:

N

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I-IMCJIO nporpaMM, KOTOPb1e npe06pa3YK)T t-IMCJIO 1 B t-IMCJIO 1, paBH0 1. 3T0 nycrrafl nporpaMMa (He cogxepxwr 1--1M OAHOi HHCTPYKAHM). 3a11H1.ueM OTO 3HaqeHne B  F(l). Tenepb 6ygxeM noCJ1eAOBaTeJ1bHO, Hat-Il-maq CO CJ1eAYK)1-qeÜ HI-leiKM (N = 2), aHaJIH3MPOBaTb, I-cal-cnx quceJ1 MOX•ceT 6b1Tb nonyqeH0 11MCJIO N. TaK, Hanpvnaep, N = 2 MO%€err 6b1Tb 110J1yqeH0 M3 N = 1 111)M6aBJ1eHneM 1, HJIM N = 1 YMHoxceHqervf Ha 2. Ilonyqaervf, wro F(2) = F(l) + F(l) — 1 + 1 = 2. 3a11M111ervf B qqei-

I-IPH AaHHb1X I-COMaHAax (+1 n *2) oqeBMAHO, wro 1--1eqeTHb1e N Moryr 6b1Tb nonyqeHb1 TOJ1bKO KOMaHAOü «+1» M3 npeAb1AY1gero N (H3 N — 1). 3Haqwr, AJ1fl 1--1HX Mbl 6YAera ganncb1BaTb TO xe T-IHCJIO, q rro B coceAHeü CJ1eBa aqeiKe. To eCTb, F(3) = F(2) = 2. A geTHb1e N MOryT 6b1Tb r10JIYqeHb1 rral-cme nyrreM YMH0%€eHHfl N/ 2 Ha 2. To ecTb, F(N) = F(N — 1) + F(N/2). Hanpn»aep, F(4) — - - 1) + F(4/2) - F(3) + F(2) -  4. TaKHM 06paaoM, 110CJ1eÅOBaTeJ1bHO gallOJIHflf1 aqeiKH, 110JIYYHM:

N

1

2 3 4

5 6 7 8

9

10

11

12

13

14

15

16

17

18

19

20

21

 

 

 

 

 

4

6

6

10

 

14

14

20

20

26

 

 

 

 

 

 

 

5.34. Y MC110JIHn rreJ1fl YABOUTeJ1b ABe I-COMaHAb1, KOTOPb1M 11PMCBoeHb1 H0Mepa:

1.     IIPH6aBb 1,

2.     YMHO%Cb Ha 2.

IlepBafl M3 1--1MX YBeJIMt1MBaeT I-IMCJIO Ha 3KpaHe Ha 1, BTopaa YBeJIHt1HBae rr t1HCJIO Ha 3KpaHe BABOe. IIporpaMMa Y ABOMTeJ1fl — OTO 110CJ1eÅOBaTeJ1bHOCTb I-COMaHA. CKOJ1bKO eCTb liporpaMM, KOTOPb1e HHCJIO 2 npe06pa3YK)T B HHCJIO 25?

5.35. Y HC110JIHn rreJ1fl Y ABOMTeJ1b ABe I-COMaHAb1, KOTOPb1M 11PHCBoeHb1 H0Mepa:

1.     IIPH6aBb 1,

2.     YMHO%Cb Ha 2.

FlepBafl 1--1HX YBeJIHHHBaeT MHCJIO Ha 0KpaHe Ha 1, BTopaa YBeJIMT-1HBaeT T-IMCJIO Ha 3KpaHe BABOe. IlporpaMMa AJ1fl YABowreJ1fl — OTO 110CJ1eAOBarreJ1bHOCTb KOMaHA. CKOJ1bKO ecTb nporpaMM, KOTOPb1e LIHCJIO 4 npe06pa3YK)T B T-IMCJIO 29?

5.36. 1--lnxce Ha qeTb1pex H3b1Kax garrncaH peKYPCHBHb1i a.mropMTM F.

 

BeicHK

IlaCKaJ1b

SUB F (n)

PRINT n IF n <-

END IF

END SUB

4 THEN

2)

1)

procedure F (n: integer) ; begin write In (n) ; if n <= 4 then begin

2 ) ; 1 ) ; end end

Си

 

Алгоритмический язык

void F(int п)

printf (”%d\n” , if (п <= 4)

2 ) ;

               1 ) ;

п) ;

алг Е (цел п) нач вывод п, нс если п <= 4 то

все кон

Чему равна сумма всех чисел, напечатанных на экране при выполнении вызова F(2)?

Решение.

Выполнение рекурсивного алгоритма можно представить следующим образом: каждый рекурсивный вызов процедуры F порождает в памяти компьютера новую копию этой процедуры и запускает ее на выполнение со своими значениями входных параметров. После того как процедура F завершила работу (возможно, в процессе работы ей пришлось породить и вызвать несколько своих копий с соответствующими входными параметрами), выполнение программы продолжается со следующего оператора после вызова Р. Здесь важно понимать, что разные копии процедуры Р, порожденные одним рекурсивным вызовом, могут одновременно находиться в памяти компьютера на разных этапах своего выполнения и иметь различные значения своих локальных переменных. Для наглядности представим схему рекурсивных вызовов в виде дерева. Поскольку в процедуре F имеются два рекурсивных вызова F(n*2) и F(n + 1), то наше дерево будет двоичным. Каждый узел дерева будет соответствовать вызову процедуры F(x). Потомками каждого узла дерева будут вызовы из процедуры Р, соответствующей узлу. Левым потомком будет вызов вида F(n*2), правым — F(n + 1). Корнем дерева будет самый первый вызов F(2). Вызвали F (2*2) = F(4), сразу напечатали 2.

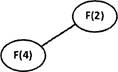
Напечатали 4. Затем проверяем условие (4<=4 истина), поэтому пошел следующий вызов F

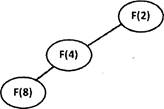
Напечатали 8. Проверяем условие (8<=4 — ложь), поэтому тело условного оператора не выполняется, данная копия процедуры F заканчивает работу и выполнение программы продолжается в копии F(4) с оператора вызова F (4 + 1), т.е. с F(5).

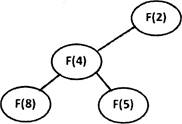
14 З

Напечатали 5. Проверяем условие (5<=4 — ложь), поэтому тело условного оператора не выполняется, данная копия процедуры F заканчивает работу и выполнение программы продолжается в копии F(2) с оператора вызова F (2 + 1), т.е. с F(3).

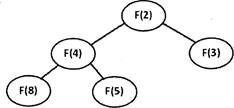
Действуя аналогично, получаем полное дерево всех рекурсивных вызовов

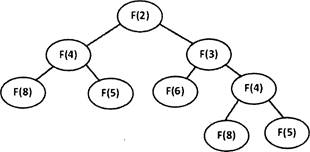
Нетрудно заметить, что поскольку значение входного параметра процедуры печатается каждый раз при вызове процедуры, искомая сумма равна сумме чисел в узлах дерева

= 45.

Замечание 1. Построенное дерево позволяет ответить на более сложный вопрос: «что напечатает программа?» Выписав значения узлов в порядке построения, получим: 2 4 8 5 З 6 4 8 5

Замечание 2. Результат работы программы при ином расположении оператора печати п, в общем случае, отличается от данного. Например, такая процедура F (Паскаль)

procedure F (п: integer) ; begin if п <= 4 then begin write1n (п) ;

end end

напечатает только значения, большие или равные четырем (при том же дереве рекурсивных вызовов), т.е. 2 4 З 4, и сумма их будет, соответственно, 13. Будьте внимательны при выполнении подобных заданий.

Второй способ решения. Так как нас интересует только итоговая сумма, будем считать, что рекуррентная функция результатом своей работы выдает на экран определенную сумму чисел. Например, будем считать, что F(n) сумма чисел, которые будут выведены на экран при вызове F(n). Будем последовательно вычислять значение этой функции (аналогично задаче 5.33).

Для начала составим рекуррентные выражения по приведенной программе.

Легко заметить, что если п > 4, то F(n) = п (подпрограмма выводит только число п и больше ничего не делает, потому что условие п <= 4 не выполняется)

А если п <= 4, то F(n) = п + F(2n) + F(n + 1). Потому что подпрограмма выводит на экран число п, а также вызывает F(2*n) и F(n + 1), которые, в свою очередь, добавляют на экран соответствующую сумму чисел. Все эти числа мы и складываем.

Применяем полученные формулы, начиная с тех значений F(n), которые очевидны и встречаются при выполнении программы. Так как нам нужно вычислить F(2), которая зависит от функции для больших значений п, будем вычислять F(n) от ббльших значений к меньшим. Начнем с F(8), так как наибольшее значение п, при котором будет вызываться F(n) это

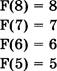
Для всех этих F(n) результат был очевиден, потому что п > 4. Следующие значения F(n) будем вычислять по формуле для п <= 4: F(n) = п + F(2n) + + 1). F(4) = 4 + + 1) = 4 + F(8) + F(5) = 4 + 8 + 5 = 17

F(3) = З + + 1) = З + F(6) + F(4) = З + 6 + 17 - 26

F(2) = 2 + + 1) = 2 + F(4) + F(3) = 2 + 17 + 26 = 45

Получили тот же ответ 45. При наличии на экзамене свободного времени рекомендуем решать задачу обоими способами, чтобы можно было сверить ответы.

5.37. Ниже на четырех языках программирования записан рекурсивный алгоритм Р.

Бейсик

 

Паскаль

SUB Е (п)

4 THEN

2)

1)

END IF

PRINT п

END SUB

 

procedure begin if п <= begin

F (n + end; write1n end

Е (п: integer) ;

4 then

2) ;

1 ) ;

(п) ;

Си

 

Алгоритмический язык

void F (int п)

if (п <— 4)

2) ;

1 ) ;

printf ( ,

п) ;

алг F (цел п) нач если п <= 4 то

все вывод п, нс кон

YKaycwre qepea gallflTYK) 110CJ1eAOBarreJ1bHOCTb BblBOAHMb1X qncen, B TOM nopflAKe I-caK uX Haneyarraerr nporpaMMa Bb1110JIHeHHH Bb130Ba F(2).

5.38. Hmxce Ha qeTb1pex fl3b1Kax nporparuranp0BaHH$1 aanncaH peKypcHBHb1ii anropHTM F.

 

Beicmc

 

llameaJ1b

SUB F (n)

IF n <=

PRINT

END IF

END SUB

4 THEN 2 ) n

1 )

 

procedure F (n: integer) ; begin if n <— 4 then begin

write In (n) ;

end; end

 

CH

 

A.mrOPHTMHyeCKHi %3b1K

void F (int n)

if

           print f       ,

n) ;

ajlll F (men n)

Haq n <= 4 TO

2 )

BblBOX1 n,

1 )

BCe

ROH

YK&KHTe qepeg gallflTYK) nocueAOBaTeJ1bHOCTb BblBOAMMb1X qncen, B TOM nopaxvce I-car-C HaneqarraeT nporpaMMa Bb1110J11--1e1--1UU Bb130Ba F(2).

5.39. Hnxce Ha qeTb1pex R3b1Kax nporpaMMnpoBaHHH ganncaH peKypcHBHb1ii anropHTM F.

Beicmc

 

Ilauca.llb

SUB F (n)

IF n > 1 THEN

2)

PRINT n

END IF

END SUB

procedure F (n: integer) ; begin if n > 1 then begin

2 ) ; write In (n) ; F (n div 2) ;

 

 

Aaro HTMHyeCKHi

void F (int n)

if

2 ) ; print f   ,

n) ;

ajll' F (I-ten n)

Hat-I eCJ1b•f n > 1

 2)

BblBOÄ n,

F (div (n,

BCe KOH

TO

HC

2) )

YKaycwre qepe3  110CJ1eAOBaTeJ1bHOCTb BblBOÄHMb1X qncen, B TOM nopaAÆ€e KaK Haneqarraerr nporpaMMa npn Bb1110JIHe1--1HH Bb130Ba F(6).

5.40. Hnxce Ha yeTb1pex H3b1Kax ganncaH peKYPCHBHb1Ü a.nropHTM F.

 

BeiCHK

IlaCKaJ1b

 

SUB F (n)

PRINT n

END IF

END SUB

THEN

2)

2 )

procedure F (n: integer) ; begin writeln (n) ; if n > 1 then begin

2 ) ;

F (n div 2) ; end; end

 

 

Си

Алго итмический язык

 

void F (int п)

printf ( , п) ; if (п > 1)

2 ) ;

алг F (цел п) нач вывод п, „нс если п > 1 то

2)

F (div (п, 2) ) все кон

Укажите через запятую последовательность выводимых чисел, в том порядке как их напечатает программа при выполнении вызова F(5).

5.41. Исполнитель Чертежник перемещается на координатной плоскости, оставляя след в виде линии. Чертежник может выполнять команду сместиться на (а, Ь), где а, Ь целые числа. Эта команда перемещает Чертежника из точки с координатами (х, у) в точку с координатами (х + а; у + Ь).

Например, если Чертежник находится в точке с координатами (4, 2), то команда сместиться на (2, —3) переместит Чертежника в точку (6, —1).

Цикл

ПОВТОРИ число РАЗ последовательность команд КОНЕЦ ПОВТОРИ означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).

Чертежнику был дан для исполнения следующий алгоритм (буквами п, а, Ь обозначены неизвестные числа):

НАЧАЛО сместиться на (З, З) ПОВТОРИ п РАЗ сместиться на (а, Ь) сместиться на (27, 12)

КОНЕЦ ПОВТОРИ сместиться на (—27, —12)

КОНЕЦ

После выполнения этого алгоритма Чертежник возвратился в исходную точку. Какое из приведенных ниже чисел обозначено буквой п?

Решение.

Анализируя принцип работы Чертежника, замечаем, что его перемещение по каждой из координат (х, у) не зависит от перемещения по другой координате. Значит, перемещение по каждой координате можно рассматривать независимо.

Запишем суммарное перемещение Чертежника по оси Х после выполнения всей программы: З + п*(а + 27) — 27. Так как цикл выполняется п раз, команды +а и +27 учитываем п раз (умножаем (а + 27) на п). Так как известно, что Чертежник вернулся в ту же точку, это суммарное перемещение равно нулю. Получаем: З + п*(а + 27) — 27 = О.

Аналогично по оси У получаем: З + n*(b + 12) 12 = о.

В обоих уравнениях оставим п, умноженное на что-то, в левой части, а остальное перенесем в правую часть и вычислим.

Получим:

+ 27) = 24

+ 12) = 9

Так как п — количество повторений цикла, п — целое неотрицательное число.

Из первого уравнения получаем, что п является делителем числа 24, из второго — делителем числа 9. У этих двух чисел (24 и 9) общими делителями являются только числа 1 и З. Числа 1 среди предлагаемых ответов нет. Значит, это число З.

5.42. Исполнитель Чертежник перемещается на координатной плоскости, оставляя след в виде линии. Чертежник может выполнять команду сместиться на (а, Ь), где а, Ь целые числа. Эта команда перемещает Чертежника из точки с координатами (х, у) в точку с координатами (х + а; у + Ь).

Например, если Чертежник находится в точке с координатами (4, 2), то команда сместиться на (2, —3) переместит Чертежника в точку (6, —1).

Цикл повтори число РАЗ последовательность команд КОНЕЦ ПОВТОРИ означает, что последовательность команд будет выполнена указанное число раз (число должно быть натуральным).

Чертежнику был дан для исполнения следующий алгоритм (буквами п, а, Ь обозначены неизвестные числа):

НАЧАЛО сместиться на (З, 5)

ПОВТОРИ п РАЗ сместиться на (а, Ь) сместиться на (15, 5) КОНЕЦ ПОВТОРИ сместиться на (—17, —40)

КОНЕЦ

После выполнения этого алгоритма Чертежник возвратился в исходную точку. Какое из приведенных ниже чисел обозначено буквой п?

5.43. Ниже на четырех языках приведена программа. Определить, при скольких различных значениях программа печатает тот же результат, что и при К = 100 (включая К = 100).

 

Паскаль

Си

function f (п: integer) :integer; begin п       п        п end; var k, i :integer;

BEGIN read1n (К) ;

whi1e f (i) >k do i:=i—1; write                      END•.

int f(int п)

    return п      п     п;

void main ( )

int К, i; scanf                                 , &k) 1   12; whi1e (f (i) >k) i-  printf (”        , i) ;

Бейсик

Алгоритмический язык

лм К, AS INTEGER INPUT К

12

WHILE F(I) > К

WEND

PRINT

FUNCTION F(N)

END FUNCTION

алг нач цел К, i ввод К i          12 нц пока F (1) > К     i      1 кц вывод кон алг цел F (цел п) нач знач     п         п  п кон

Решение. Сначала вычислим, какой результат выдает программа при указанном К = 100. Функция f(n) вычисляет куб числа п. Цикл WHILE уменьшает значение переменной i от 12 и меньше, пока f(i) > К. То есть, пока i > 100. Как только это перестает выполняться, цикл оканчивается. То есть, как только i становится 100. Самое большое значение i, при котором i3 100 — это 4 (4 3 = 64, 5 3 уже 125 > 100). Чтобы найти все такие К, при которых программа выводит тот же ответ, нужно найти все такие К, при которых 43 < К, а 5 3 > К. Получаем неравенство: 64 < 125. Нам нужны все целые значения К. Это от 64 до 124. То есть, 124 - 64 + 1 = 61.

5.“. Ниже на четырех языках приведена программа. Определить, при скольких различных значениях К программа печатает тот же результат, что и при К = 150 (включая К = 150).

 

Паскаль

Си

 

 

function f (п: integer) begin f п п п end; var k, i :integer;

BEGIN read1n (К) ;

whi1e f (i) >k do i:=i—1; write (i) ;

END.

:integer;

п

int f (int п)

    return п     п     п

void main ( )

int К, i; scanf ( 'I2 d II , &k) ; i   12; whi1e (f (i) >k) i—     printf ( но6d    i) ;

п;

Бейсик

Алгоритмический язык

 

DIM К, AS INTEGER

INPUT К

12

WHILE F(I) > К

1

WEND

PRINT

FUNCTION F(N)

END FUNCTION

алг нач цел К, i ввод К i        12 нц пока F (i)

                                          1 кц вывод 1 кон алг цел F (цел п) нач знач  п      п

кон

п

п

 

5.45. Получив на вход число х, алгоритм печатает два числа L и М. Укажите наибольшее из таких чисел х, при вводе которых алгоритм печатает сначала 12, а потом З.

Паскаль

Си

var х, L, М: integer; begin• read1n (х) ; о; м     о; while      do begin м   

L + х mod 10; х   х div 10; end; write1n (L) ; write (М) ;

void main ( )

int х, ь, М; scanf ( 6d       &х) ; о;

whi1e (х > 0)

м

            х                 

printf ( ,

Бейсик

Алгоритмический язык

DIM Х,

INPUT

WHILE м

х

WEND

PRINT

PRINT

ь, М AS INTEGER х

> о

М         1

Х MOD 10

10

м

алг нач цел х, L, м ввод х

нц пока х > О м

L + mod(x, 10) х   div (х, 10) кц вывод L, нс, М кон

Решение. Анализируем, что делает алгоритм. Исходное число х в цикле, пока оно больше нуля, делят на 10 и что-то делают с остатками от деления на 10. Это известный алгоритм перевода числа в другую систему счисления (в данном случае в десятичную). То есть, выделение десятичных цифр из числа. На каждом шаге цикла переменная М увеличивается на 1. Это счетчик количества итераций цикла. Сказано, что он становится равен 3-м. Значит, было выделено З цифры числа. Значит, число х трехзначное. Во время работы цикла цифры числа добавляются к переменной L. Это сумма цифр числа. Сказано, что она становится равна 12. Остается только подобрать такое наибольшее трехзначное число, сумма цифр которого равна 12-ти. Чтобы число было наибольшим, первой цифрой поставим самое большое, что можно — это цифра 9. Сумма оставшихся цифр остается равной 3-м (12 — 9 = З). Вторая цифра тоже должна быть наибольшей из возможных. Эго цифра З. Последняя цифра остается — О. Ответ — 930.

5.46. Получив на вход число х, алгоритм печатает два числа L и М. Укажите наименьшее из таких чисел х, при вводе которых алгоритм печатает сначала З, а потом 16.

Паскаль

Си

var х, L, М: integer; begin read1n (х) ; 9; м о; whi1e х do begin м     М + х mod 10; if х mod 10 < L then х mod 10; х   х div 10; end; write1n (L) ; write (М) ; end.

#inc1ude<stdio . void main ( )

int х, L, М; scanf     , &х) ;

          9;

whi1e (х > 0)

if (х о 10 < ы

Х о х printf (”%d\n%d” ,

Бейсик

Алгоритмический язык

DIM Х, L, М АБ INTEGER INPUT х

9

WHILE м           М + Х MOD 10

IF Х MOD 10 < L THEN

Х MOD 10

END х     х \ 10

WEND

PRINT

PRINT м

алг нач цел х, L, м ввод х 9

0 нц пока х > 0

М + mod (x, 10) если mod (х, 10) < L то mod (х, 10) все х div (х, 10) кц

вывод Ь, нс, М кон

5.47. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1)   Строится двоичная запись числа N.

2)   К этой записи дописываются справа еще два разряда по следующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, которое превышает 43 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.

Решение. Наименьшее число, которое превышает 43, число 44. Переведем его в двоичную систему счисления. Получим 1011002. Проверим, может ли оно быть получено приведенным алгоритмом. В результате алгоритма к двоичному представлению числа добавляется две двоичные цифры. Возьмем первые цифры числа, кроме последних двух и применим к ним алгоритм. В результате действия а) получаем 1 + О + 1 + 1 = З. В остатке от деления на 2 — 1. А в двоичной записи числа 44 на этом месте стоит цифра О. Значит, число 44 не подходит. Однако то, что оно не подходит, еще не означает, что начальная часть числа не подходит. Первую цифру мы уже вычислим. Вычислим вторую: 1 + О + 1 + 1 + 1 = 4. Остаток от деления на 2 равен О. Получаем двоичное число 1011102. Переведем его в десятичную систему. Получаем 46. Так как мы получили его по приведенному алгоритму и оно больше 43, это и есть ответ.

5.48. То же условие, что и в 5.46, но нужно найти минимальное число, превышающее 41.

Решение. Переведем число 42 в двоичную систему. Получаем 1010102. Применяем алгоритм к первым цифрам 10102. Получаем 1010002. Это число 40. Оно нам не подходит, так как меньше 41. Наименьшее число, которое может нас устроить — следующее. То есть, оно получается из числа, следующего после 10102. Это число 10112. Применим в нему алгоритм. Получим 1011102. Это 46.

5.49. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число V следующим образом.

1.  Строится двоичная запись числа N.

2.  К этой записи дописываются справа еще два разряда по следующему правилу:

а) складываются все цифры двричной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа У.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 46. В ответе это число запишите в двоичной системе счисления.

Рекомендации. Аналогично предыдущей задаче, берем наименьшее число, большее 46 (это 47) и переводим его в двоичную систему счисления (получится, кстати, 6 разрядов). Далее проверяем, верно ли, что по первым 4-м разрядам можно посредством алгоритма получить оставшиеся два разряда. Если совпало — эти 4 разряда есть ответ. Если не совпало — сравниваем полученное двухразрядное двоичное число с тем, что стоит в конце числа 47. Если полученные 2 разряда больше имеющихся в числе 47 — первые 4 разряда и есть ответ. Если больше — в ответ записываем следующее двоичное 4-разрядное число (можно получить прибавлением 1).

5.50. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1)   Строится двоичная запись числа N.

2)   К этой записи дописываются справа еще два разряда по следующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R.

Укажите минимальное число R, которое превышает 56 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.

5.51. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число V следующим образом.

1.  Строится двоичная запись числа N.

2.  К этой записи дописываются справа еще два разряда по следующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа V.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 49. В ответе это число запишите в двоичной системе счисления.

5.52. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число V следующим образом.

1.  Строится двоичная запись числа N.

2.  К этой записи дописываются справа еще два разряда по следующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописы вается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа V.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 54. В ответе это число запишите в двоичной системе счисления.

5.53. Напишите в ответе число, равное количеству различных значений входной переменной К, при которых приведенная ниже программа выводит тот же ответ, что и при входном значении К = 10. Значение К = 10 также включается в подсчет различных значений К. Для Вашего удобства программа приведена на пяти языках программирования.

 

BeicHK

 

IIHTOH

DIM K, 1 AS LONG

INPUT

    1  1

WHILE

    1 1 + 1

WEND

    IF F (1 ) -K  K-F(I-I)

PRINT 1

ELSE

PRINT 1-1

END IF

FUNCTION F (N)

END FUNCTION

THEN

def return n* n *n

i 1 k  int (input ( ) ) while f (i) < k:

i+=l if (f (i) —k <= k—f (i-1 ) ) : print (i) else:

print (i  1)

Amo HTMHqeCKHi

TlacxaJ1b

 

ajlll

Haq

I-ten i, k BBOÄ k

         i    1

HI-I r10Ka f (i) <

eCJ11.•f f (i) —k <=

BblBOÄ i

YlHaqe

BblBOZ1 i —1

BCe

KOH aril' men f (men n)

Haq

         3Haq        n

KOH

k

k—f (i —1) n

var longint;

function f (n : begin

         f    n   n

begin

read In (k) ; i   1 ; while f (i) <

if f (i) —k <— write In (i)

write In (i —1) end

long int) n;

k do

k—f (i —1)

;

longint;

then

 

# include <stdio.h> long f (long n)

           return n   n   n;

void main ( )

long k, i; scanf ("%ld" , i 1 ; while (f (i) < k)

if (f (i) —k <= print f ("%ld" , i) ;

print f ( " %ld"

Pemco.ueHDauuu.

CHaqua Bblt1HCJIHM, T-ITO BblBOAHT nporpaMMa npn k = 10.

B 1.1MKJ1e neperaeHHaa i Mel--1He rrca 0T 1 Ha 1, 1101-ca i < 10. To eCTb, i 3 < 10 nepecTaHerr Bb1110JIHHTbCfl (TO eCTb, 6ymerr i 3 10). 2 3 = 8, 3 3 IIOACTaBMM erro i = 3 B cneÅYK)11xee ycJ10Bne: f(i) — k <= k — f(i — 1). 33

27 - 10 s 10 - 8? HeT.

3Haqnrr, Ha 3KpaH 6yaeT BblBeaeHO (i — 1). To eCTb, 2.

I-rpm HeKOTOPOM i BblpaxceHue

27. 3Haqwr, OTO i = 3. 10 10 - 23 ?

Tenepb HaÜAeM,       I-caKMX k liporpaMMa 6YÅerr BblBOAUTb Ha 3KpaH 2.

3T0 MOX€eT 6b1Tb npn BblBOÅe (i — 1), I-cal-C B paCCMOTPeHHOM cnyqae k = 10. A traycxce npu BblBoae i (ecJIH YCJ10Bne f(i) —k <= k — f(i — 1) Bb1110JIHHTCH.

PaccraorrpHM nepBb.1i cnyqai. Ha 3KpaH BblBOAHTCfl (i — 1). YCJ10BHe He Bb1110JIHHJIOCb.

Ilpn 3TOM i = 3 ycJ10Bne 6yaerr: 3 3 — k > k — 2 3 . 27 — k > k — 8. 35 > 2k. k < 17,5. TaK I-cal-C k — genoe IIHCJIO, TO OTO YCJ10Bne paBHOCHJ1bHO k 17.

3T0 Mbl paccM0TpeJIH YCJ10Bne BblBOAa Ha 3KpaH. El.qe HY%CHO, HT06b1 nocne OKOHqaHUfl 1.1HKJ1a nepervfeHHaa i 6b1J1a paBHa 3. To eCTb,     i = 2 YCJ10Bne 1.1HKJ1a Bb1110JIHaeTCfl.• f(i) < k. 23 < k. K > 8. A IIPH i = 3 YCJ10Bue 11HKJ1a nepec rraerr Bb1110JIHflTbCfl: f(i) k. 3 3 k. k 27.

06'beÅHHaervf (BepHee, nepeceKaeM) BCe TPA YCJIOBHfl (k 17, k > 8, k 27) n no.nyqaeM 8 < k 17.

PaccMOTPHM BTOPOi1 cnyyai. Ha 3KpaH BblBOÅHTCfl (i). YCJ10Bne Bb1110JIHHJIOCb.

Ilpu 3TOM i = 2 ycJ10Bne 6ymerr: 2 3 — k k — 1 3 . 8 — k k — 1. 9 2k. k 4,5. TaK I-cal-C k — genoe T-MCJIO, TO 3T0 ycJ10Bne paBHOCHJ1bHO YCJIOBmo k 5.

I-IT06b1 nocne OKOHqaHMfl 1.1MKJ1a nepeMeHHaa i 6b1J1a 6b1 paBHa 2, HY%CHO 11T06b1 i = 1 YCJ10Bne

1.1MKJ1a euxe Bb1110JIHflJIOCb: 1 3 < k. k > 1.

A     i = 2 YCJ10Bne gnKJ1a AOJI)KHO nepecTaTb Bb1110JIHflTbCfl: 2 3 k. k 8.

06'beAHHfler.a (BepHee, nepeceKaeM) BCe TPA YCJIOBHfl (k 5, k > 1, k 8) H 110.nyqaeM 5 k S 8. 06'beAHHaer•a YCJIOBMH nepB01'0 BToporo cnyqaeB 110J1yqaeM 5 k 17. OT 5 AO 17 110J1yqaeM 13 pa3JIVNHb1X 3HaqeHHii nepervreHH0ii k.

5.54. HarlH111HTe B OTBeTe T-IHCJIO, paBHoe KOJInqeCTBY pa.3JIHt1Hb1x 3HaqeHHi BXOAHOM nepervreHHoi k, KOTOPb1X lipHBeAeHHaa 11porpaMMa BblBOAMT TOT xe OTBeT, q rro n npn BXOAHOM 3HaqeHHH k = 30. 3HaT-1eHne k = 30 rral-cxce BKJnoqaeTCfl B noacqerr pae3JIHMHb1X 3HaqeHMii k. AJ1fl Bamero YA06CTBa nporpaMMa lipMBeAeHa Ha 11flTH fl3b11-cax nporpaMr.anpoBaHHfl.

BeiCHK

 

IIHTOH

 

DIM K, i AS LONG INPUT K

    1  1

WHILE F (1) < K

1 - 1 + 1

WEND

IF F (1) F (1-1) PRINT 1

ELSE

PRINT 1-1

END IF

FUNCTION

                           N    30

END FUNCTION

> K

THEN

def f (n) :

return n*n—30 i  1 k  int (input ( ) ) while f (i) i+=l if (f (i)  print (i) else:

                print (i   1)

 

 

Алго итмический язык

 

Паскаль

алг нач цел i, К ввод К i       1 нц пока f (i ) < К

кц           если f (i) — f(i—1) вывод i иначе вывод все кон алг цел f (цел п) нач знач  кон

> 

К то

 

var

. 10ngint; function f (п: 10ngint) • 10ngint; begin f п п end; begin read1n (К) ; i   1; whi1e f (i ) < К do

if f (i ) f(i—1) > К then writeln (i)

writeln (i—1) ; end.

 

 

 

Си

#inc1ude <stdio.h>

1опд f (long п)

     return п     п

void main ( )

long К, i; scanf     , &k) ; i  1; while (f (i) < К)

if (f (i) f(i—1) printf ,

       printf       

> 

К)

5.55. Напишите в ответе число, равное количеству различных значений входной переменной К, при которых приведенная ниже программа выводит тот же ответ, что и при входном значении = 40. Значение К = 40 также включается в подсчет различных зна чений К. Для Вашего удобства программа приведена на пяти языках программирования.

Бейсик

 

 

Питон

лм К, AS LONG INPUT К 100

WHILE F(I)

WEND

F(I-1)

PRINT

ELSE

PRINT 1-1

END IF

FUNCTION

                       1)

END FUNCTION

20

THEN

def f (n) :

return п * (п— 1) i  100

К    int (input ( ) ) whi1e f ( i) i—=1 if (f (i)       f(i—1) print (i)

print (i  1)

Алго итмический язык

Паскаль

алг

нач цел 1, К ввод К i        100 нц пока f (i) > К i 1  1

кц если f (i) f(i—1) вывод i

иначе вывод i—1 все     

кон алг цел f (цел п)

нач знач   (п 1)

кон

20

то

var

• longint; function f (п: 10ngint) begin

f .   п       (п  1 ) ; end; begin read1n (К) ;               100; while f (i) > К do                1; if f (i)        f (i-1 )                        write1n (i)

write1n (i—1) ;

10ngint;

20 then

 

 

 

Си

 

#include <stdio.h>

1опд f (long п)

     return п      (п

void main ( )

1опд К, i ; scanf %ld t' , &k) ; i  100; whi1e (f (i) > К)

if ( f ( i )  f(i—   printf  i ) ;

      printf (”%1d i—1) ;

К       20)

 

 

5.56. Исполнитель Апрель15 преобразует число на экране.

У исполнителя есть две команды, которым присвоены номера:

1.  Прибавить 1

2.  Умножить на 2

Первая команда увеличивает число на экране на 1, вторая умножает его на 2.

Программа для исполнителя Апрель15 — это последовательность команд.

Сколько существует программ, для которых при исходном числе 1 результатом является число 21 и при этом траектория вычислений содержит число 10?

Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

Решение. Так как по условию «траектория вычислений» должна содержать число 10, получаем, что число 10 должно обязательно содержаться в последовательности преобразований числа 1 в число 21. То есть нужно отдельно посчитать количество вариантов получения числа 10 из числа 1 и количество вариантов получения числа 21 из числа 10, а после перемножить результаты. И то и другое можно сделать уже знакомым нам способом. Например, построим таблицу, в которой будем последовательно вычислять число вариантов получения числа п из числа 1 (где п будет меняться от 1 до 10). Обозначим F(n) — число вариантов получения числа п из числа 1. Очевидно, что F(1) — 1 (число различных программ, которые состоят из приведенных команд 1 и 2 и получают из числа 1 число 1 — одна (в ней нет ни одной команды)). Если п — нечетное, то F(n) = F(n — 1).

А если п — четное, то F(n) = F(n — 1) + F(n/2).       Строим таблицу:

 

1

2

 

4

5

6

7

8

9

10

 

1

2

2

4

4

6

6

10

10

14

Число вариантов получения из 10 числа 21 проще посчитать, построив дерево возможных преобразований. Оно получится весьма примитивным, потому что после первого же действия (10 + 1 11 и 10 • 2 = 20) получаются числа, из которых 21 можно получить только одним способом — прибавляя единицу. То есть, из 10 можно получить 21 только двумя различными программами.

Перемножаем ответы 14 • 2 = 28.

Заметим, что так как при построении таблицы возможны арифметические ошибки, рекомендуем для проверки построить также дерево возможных преобразований из 1 в 10 и убедиться, что число вариантов в дереве совпадает с числом вариантов, полученных таблицей.

 5.57. Исполнитель Июль2О преобразует число на экране.

У исполнителя есть две команды, которым присвоены номера:

1.  Прибавить 1

2.  Умножить на 2

Первая команда увеличивает число на экране на 1, вторая умножает его на 2.

Программа для исполнителя Июль2О -г это последовательность команд.

Сколько существует программ, для которых при исходном числе 1 результатом является число 24 и при этом траектория вычислений содержит число 8?

Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

5.58. Исполнитель Июль2О преобразует число на экране.

У исполнителя есть две команды, которым присвоены номера:

1.  Прибавить 1

2.  Умножить на 2

Первая команда увеличивает число на экране на 1, вторая умноэкает его на 2.

Программа для исполнителя Июль2О — это последовательность команд.

Сколько существует программ, для которых при исходном числе 2 результатом является число 37 и при этом траектория вычислений содержит число 15?

Траектория вычислений программы это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

5.59. Исполнитель Июль2О преобразует число на экране.

У исполнителя есть две команды, которым присвоены номера:

1. Прибавить 1

2. Умножить на 2

Первая команда увеличивает число на экране на 1, вторая умножает его на 2.

Программа для исполнителя Июль2О — это последовательность команд.

Сколько существует программ, для которых при исходном числе З результатом является число 39 и при этом траектория вычислений содержит число 17?

Траектория вычислений программы — это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 16, 17.

5.60. Исполнитель Редактор получает на вход строку цифр и преобразовывает ее. Редактор может выполнять две команды, в обеих командах и w обозначают цепочки цифр.

А) заменить (о, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Например, выполнение команды заменить (222, 34) преобразует строку 77222277 в строку 7734277.

Если в строке нет вхождений цепочки и, то выполнение команды заменить (и, w) не меняет эту строку. Б) нашлось

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл

ПОКА условие последовательность команд КОНЕЦ ПОКА выполняется, пока условие истинно.

В конструкции

ЕСЛИ условие

ТО команда1

ИНАЧЕ команда2 КОНЕЦ ЕСЛИ выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 95 идущих подряд цифр 7? В ответе запишите полученную строку.

НАЧАЛО

ПОКА нашлось (777) ИЛИ нашлось (888)

ЕСЛИ нашлось (777)

ТО заменить (777, 8)

ИНАЧЕ заменить (888, 7)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

Решение. Выполним приведенный алгоритм.

На первом этапе каждые три первых 777 меняются на одну 8.

В строке исходно 31 тройка 777. Поэтому в результате получится строка, в которой в начале 31 цифра 8, затем оставшиеся две цифры 7.

Теперь алгоритм будет заменять первые 888 на 7. Затем вторые 888 на 7. Затем третьи 888 на 7.

После этого в строке снова найдется 777, которые будут заменены на 8.

То есть из 31-й восьмерки сначала 9 первых будет заменено на 777. Затем эти 777 снова на 8.

То есть получим в строке сначала 31 — 9 + 1 = 23 восьмерки, затем 77.

На следующем этапе, аналогично, в строке останется на 8 восьмерок меньше (15 восьмерок и 77).

На следующем этапе — еще на 8 меньше. Получится 7 восьмерок и 77.

Теперь первые 888 поменяются на 7 и вторые 888 поменяются на 7.

Получится 77877. В этой строке нет ни одной группы 777 или 888. Поэтому алгоритм закончится.

ответ — 77877.

5.61. Исполнитель Редактор получает на вход строку цифр и преобразовывает ее. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку ш. Например, выполнение команды  заменить (222, 34) преобразует строку 77222277 в строку 7734277.

Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, ш) не  меняет эту строку. Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл

ПОКА условие последовательность команд КОНЕЦ ПОКА выполняется, пока условие истинно.

В конструкции

ЕСЛИ условие

ТО команда1

ИНАЧЕ команда2 КОНЕЦ ЕСЛИ выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

а) Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 75 идущих подряд цифр 7? В ответе запишите полученную строку.

НАЧАЛО

ПОКА нашлось (777) ИЛИ нашлось (888)

ЕСЛИ нашлось (777)

ТО заменить (777, 8)

ИНАЧЕ заменить (888, 7)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА КОНЕЦ

б) Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 75 идущих подряд цифр 7? В ответе запишите полученную строку,

НАЧАЛО

ПОКА нашлось (777) ИЛИ нашлось (888)

ЕСЛИ нашлось (777)

ТО заменить (777, 8)

ИНАЧЕ заменить (888, 7)

                            КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

в) Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 69 идущих подряд цифр 8? В ответе запишите полученную строку.

НАЧАЛО

ПОКА нашлось (777) ИЛИ нашлось (888)

ЕСЛИ нашлось (777)

ТО заменить (777, 8)

ИНАЧЕ заменить (888, 7)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА

КОНЕЦ

6. ИНФОРМАЦИОННЫЕ МОДЕЛИ

основные понятия

В задачах ЕГЭ на анализ информационных моделей обычно используются две основные информачионные модели — таблицы и схемы. Как правило, умения понимать эти модели достаточно для решения данного рода задач.

Информация в таблице построена по следующему принципу: на пересечении строки и столбца находится информация, характеризующая комбинацию этой строки и столбца.

Пример. Таблица умножения. На пересечения строки номер Х и столбца У находится результат умножения Х на У.

Информация на схеме построена по следующему принципу: если между объектами схемы имеется связь, она отображается линией, соединяющей названия этих объектов на схеме. Пример. Схема железнодорожных станций (или метрополитена). Между двумя станциями можно проехать, если на схеме нарисована линия, соединяющая эти станции.

Практическая часть

6.1. В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.

 

 

 

 

 

 

 

 

 

 

 

 

в

1

 

 

З

 

С

4

 

 

 

2

 

 

З

 

 

 

Е

1

 

2

 

 

1)                                          2)                                       3)                                        4)

з D                               2В 1 А 4 C 3 D с

4

4 с

2

1 в

Рекомендации. Анализируем представленную информацию. Таблица отображает стоимость для всех комбинаций станций. То есть на пересечении строки Х и столбца У находится число, соответствующее стоимости проезда от станции Х до станции У. Отсутствие числа в ячейке соответствует отсутствию дороги между этими станциями.

На схеме названия станций соединены линиями с числами. Судя по всему, линия, соединяющая станцию Х со станцией У, отражает наличие пути между станциями Х и У, а число на этой линии — стоимость проезда по этому пути.

Задача нахождения соответствия между схемой и таблицей, таким образом, сводится к задаче идентичности связей и их стоимостей.

Так, по таблице из станции А можно добраться до станции В за 1, до станции С за 4, и до станции Схема 1 не соответствует этому (путь из А в Е «стоит» 2). Дальше не будем ее рассматривать.

Схемы 2, З и 4 соответствуют.

По таблице от станции В можно добраться до станции В за 1 , а до станции D за З.

Схема 2 соответствует этому. Схемы З и 4 не соответствуют этому (путь из В в D на них отсутствует).

Значит, единственным возможным кандидатом остается только схема 2.

Для подстраховки можно проверить на соответствие остальные строки таблицы. Если обнаружится несоответствие, значит, либо ошиблись составители задачи (что очень маловероятно, ибо все задания по несколько раз проверяются), либо мы были невнимательны в одной из наших предыдущих проверок и отсеяли что-то правильное.

6.2. В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.

 

 

 

 

 

 

 

 

 

 

 

 

в

1

 

2

 

 

С

4

2

 

 

 

 

 

 

 

 

з

Е

1

 

 

з

 

1)                           2) 3)        4) з D 2 с

4

2

1 в

6.3. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между- соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.

Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в В не больше б».

Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.

1

Рекомендации. Если таблица большая и плотно заполнена числами, то для решения такого рода задач требуется, вообще говоря, сложный алгоритм (например, алгоритм Дейкстры). Его изучение не входит в стандартный курс школьной информатики. Но в данном случае таблица небольшая и далеко не все ее тетки заполнены. Значит, можно ее достаточно эффективно решить, осуществив осмысленный перебор возможных вариантов.

При решении рекомендуется воспользоваться двумя соображениями:

1)     вариант пути, КОТОРЫЙ становится больше или равен 6, но еще не достигает конечной точки

(В), можно дальше не рассматриёать;

2)     возвращение в точку, через которую уже прошел путь (петля), не приведет к эффективному решению, поэтому такие ветки тоже можно не рассматривать.

Рассмотрим пример такого «осмысленного перебора»:

Таблица 1:

Из точки А два пути — в точку С (равен З) и в точку D (равен 1).

Если пошли в точку С (путь А—С), из нее три пути — в точку А (петля, не рассматриваем), в точку

В (равен 4, в сумме З + 4 = 7, больше 6, не рассматриваем) и в точку Е (равен 2, итого путь А — равен З + 2 = 5).

Из точки Е только два пути, оба равны 2, то есть сумма 5+2 будет больше 6, дальше можно не рассматривать.

Если пошли в точку D (путь A—D), из нее только путь в точку А (петля).

Все возможные пути мы отбросили, до точки В за 6 добраться не удалось, значит, таблица варианта 1 нам не подходит.

Все это решение гораздо удобнее и эффективнее рисовать при помощи небольшой схемки, на которой рисуются возможные пути из стартовой точки и для каждой точки, в которую приходит путь, указывается текущая стоимость проезда:

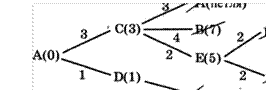Х(петля)

1 Д(петля)-

Далее нужно таким же образом рассмотреть остальные З варианта таблицы. Один из них должен  соответствовать условию.

Возможно решение этой задачи в обратную сторону, «с конца». В этом случае сначала рассматриваются все точки, из которых можно добраться до конечной точки (В). Потом — все точки, из которых можно добраться до этих, и т.д. Смысл решения точно такой же, нужно отбрасывать варианты с «петлями» и варианты, стоимость проезда в которых становится больше или равна 6. Эти два способа решения («с начала» и «с конца») в обычном случае одинаковы. Мы рекомендуем предпочесть решение «с конца», если количество путей, входящих в конечную точку, меньше, чем количество путей, выходящих из стартовой (как, например, в таблице варианта 2).

6.4. Грунтовая дорога проходит последовательно через населенные пункты А, В, С и D. При этом длина дороги между А и В равна 80 км, между В и С — 50 км и между С и D — 10 км.

Между А и С построили новое асфальтовое шоссе длиной 40 км. Оцените минимально возможное время движения велосипедиста (в часах) из пункта А в пункт В, если его скорость по грунтовой дороге — 20 км/час, по шоссе — 40 км/час?

Рекомендация. Хотя внешне задача выглядит совсем не как только что рассмотренный масс задач, решается она таким же образом. Мы рекомендуем нарисовать схему возможных путей из стартовой точки (А) и рассчитать время проезда до точек, связанных с ней. При этом нужно не забыть, что время рассчитывается как длина пути, деленная на скорость.

Потом примените тот же способ перебора, что и в предыдущей задаче (только теперь числа на линиях схемы будут показывать не стоимость проезда, а время в пути).

Когда вы рассмотрите все возможные способы проезда (которые, конечно, не содержат «петель»), выберите среди них минимальное время.

6.5. Между населенными пунктами А, В, С, D, Е, F построены дороги, протяженность которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги Между пунктами нет.)

 

 

в

с

 

 

 

 

7

з

 

 

 

в

7

2

4

1

 

с

з

2

7

5

9

 

 

4

7

2

з

 

 

1

5

2

7

 

 

 

9

З

7

Определите длину кратчайшего пути межлу пунктами А и F (при условии, что передвигаться можно только по построенным дорогам).

6.6. Между четырьмя местными аэропортами: ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО, ежедневно выполняются авиарейсы. Приведен фрагмент расписания перелетов между ними:

Аэропорт вылета

Аэропорт прилета

Время вылета

Время прилета

сосново

КРАСНЫЙ

06:20

08:35

КРАСНЫЙ

ОКТЯБРЬ

10:25

12:35

ОКТЯБРЬ

КРАСНЫЙ

11:45

13:30

БЕРЕГ

сосново

12:15

14:25

сосново

ОКТЯБРЬ

12 : 45

16:35

КРАСНЫЙ

сосново

13:15

15:40

ОКТЯБРЬ

сосново

 

17:25

ОКТЯБРЬ

БЕРЕГ

15:30

17:15

сосново

БЕРЕГ

17:35

19:30

БЕРЕГ

ОКТЯБРЬ

19:40

21:55

Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт СОСНОВО.

Рекомендация. Метод решения этой задачи такой же, как у предыдущих.

Предлагается рассматривать все возможные варианты, отбрасывая при этом те, которые хуже, чем известные.

Из стартовой точки (ОКТЯБРЬ) можно улететь в БЕРЕГ (прилет в 17:15), КРАСНЫЙ (прилет в 13:30) и в СОСНОВО (прилет в 17:25).

Значит, на данный момент нам известен маршрут, доставляющий путешественника в пункт назначения (СОСНОВО) в 17:25. Это значит, что при рассмотрении остальных маршрутов мы будем отбрасывать те рейсы, которые заканчиваются позже, чем в 17:25.

Кроме того, не имеет смысла рассматривать рейсы, которые отправляются раньше, чем путешественник оказывается в этом аэропорту. Таюке не имеет смысла возвращаться в ту точку, где путешественник уже был.

Изобразим полученное на схеме:

БЕРЕГ (17:15)

ОКТЯБРЬ (0:0)КРАСНЫЙ (13:30) сосново (17:25)

из пункта БЕРЕГ есть рейсы в СОСНОВО и в ОКТЯБРЬ. Рейс в СОСНОВО отбрасываем, так как он отправляется в 12:15, а путешественник окажется в БЕРЕГЕ только в 17:15. Рейс в ОКТЯБРЬ не рассматриваем («петля»). Значит, из ОКТЯБРЯ в БЕРЕГ лететь не нужно.

Из КРАСНОГО есть рейсы в ОКТЯБРЬ и в СОСНОВО. Первый не рассматриваем — «петля», второй отправляется раньше, чем в 13:30 (время прибытия путешественника в КРАСНЫЙ).

Получаем, что в данной задаче самый лучший вариант — лететь прямым рейсом из ОКТЯБРЯ в сосново.

6.7. Между четырьмя местными аэропортами: ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА ежедневно выполняются авиарейсы. Приведен фрагмент расписания перелетов между ними. Путешественник оказался в аэропорту ВОСТОРГ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт ГОРКА.

Аэропорт вылета

Аэропорт прилета

Время вылета

Время прилета

ВОСТОРГ

ГОРКА

16:15

18:30

ОЗЕРНЫЙ

ЗАРЯ

 

15:50

ОЗЕРНЫЙ

ВОСТОРГ

14:10

16:20

ГОРКА

ОЗЕРНЫЙ

17:05

19:20

ВОСТОРГ

ОЗЕРНЫЙ

11:15

13:20

ЗАРЯ

ОЗЕРНЫЙ

16:20

18:25

ВОСТОРГ

ЗАРЯ

14:00

16:15

ЗАРЯ

ГОРКА

16:05

18:15

ГОРКА

ЗАРЯ

14:10

16:25

ОЗЕРНЫЙ

ГОРКА

18:35

19:50

6.8. Между четырьмя местными аэропортами: ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА ежедневно выполняются авиарейсы. Приведен фрагмент расписания перелетов между ними. Путешественник оказался в аэропорту ВОСТОРГ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт ГОРКА.

Аэропорт вылета

Аэропорт прилета

Время вылета

Время прилета

ВОСТОРГ

ГОРКА

13:30

18:10

ОЗЕРНЫЙ

ЗАРЯ

14:20

16:10

ОЗЕРНЫЙ

ВОСТОРГ

14:10

16:20

ГОРКА

ОЗЕРНЫЙ

17:05

19:20

ВОСТОРГ

ОЗЕРНЫЙ

12:10

14:15

ЗАРЯ

ОЗЕРНЫЙ

12:30

14 : 40

ВОСТОРГ

ЗАРЯ

12:20

 

ЗАРЯ

ГОРКА

 

15:50

ГОРКА

ЗАРЯ

14:10

16:25

ОЗЕРНЫЙ

ГОРКА

14:25

16:30

6.9, Между четырьмя местными аэропортами: ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА ежедневно выполняются авиарейсы. Приведен фрагмент расписания перелетов между ними. Путешественник оказался в аэропорту ВОСТОРГ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт ГОРКА.

Аэропорт вылета

Аэропорт прилета

Время вылета

Время прилета

ВОСТОРГ

ГОРКА

13:10

17:15

ОЗЕРНЫЙ

ЗАРЯ

13:00

14:30

ОЗЕРНЫЙ

ВОСТОРГ

12:10

14:20

ГОРКА

ОЗЕРНЫЙ

11:15

15:30

ВОСТОРГ

ОЗЕРНЫЙ

12:35

14 : 50

ЗАРЯ

ОЗЕРНЫЙ

12:30

14:20

ВОСТОРГ

ЗАРЯ

10:30

12:15

ЗАРЯ

ГОРКА

14:40

16:45

ГОРКА

ЗАРЯ

15:15

17:20

ОЗЕРНЫЙ

ГОРКА

14:30

16:20

6.10. Между четырьмя местными аэропортами: ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА ежедневно выполняются авиарейсы. Приведен фрагмент расписания перелетов между ними. Путешественник оказался в аэропорту ВОСТОРГ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт ГОРКА.

Аэропорт вылета

Аэропорт прилета

Время вылета

Время прилета

ВОСТОРГ

ГОРКА

10:15

14:30

ОЗЕРНЫЙ

ЗАРЯ

10:20

12:30

ОЗЕРНЫЙ

ВОСТОРГ

14: 14

16:30

ГОРКА

ОЗЕРНЫЙ

15:40

17:35

ВОСТОРГ

ОЗЕРНЫЙ

10:05

12:20

ЗАРЯ

ОЗЕРНЫЙ

11:40

13:55

ВОСТОРГ

ЗАРЯ

9:40

11:50

ЗАРЯ

ГОРКА

12:20

14:10

ГОРКА

ЗАРЯ

13:15

15:40

ОЗЕРНЫЙ

ГОРКА

12:30

14:25

6.11. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. по каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

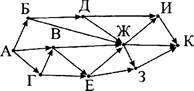
Рекомендация. Для решения этой задачи рекомендуем рассматривать для каждой вершины, начиная со стартовой, количество путей от стартовой вершины до данной. Очевидно, что для самой стартовой вершины это количество равно 1 (можно одним способом оказаться в ней — никуда не ехать). Это количество будем записывать возле каждой вершины на самой схеме. Найдем вершину, у которой у всех «стрелок», которые входят в эту вершину, известны количества путей для начальной вершины «стрелки». В данном случае таких вершин две — Б и Г. Для обеих напишем количество путей. Оно пока тоже равно 1. В эти вершины входит только по одной «стрелке», значит, число способов добраться до них такое же, как число способов добраться до предыдущей вершины (из которой выходит «стрелка»). БО

Теперь повторим эту операцию. Найдем все вершины, для которых известны числа для всех входящих «стрелок». Теперь это В и Д. для верщины Д стрелка опять одна, значит, число путей из вершины А совпадает с предыдущей вершиной (Б), то есть 1. А вот в вершину В входит 2 «стрелки». Поэтому нужно сложить числа всех вершин, из которых идут «стрелки» в данную вершину. То

есть 1 + 1 = 2.

                                               БО ДО            И

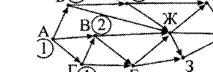ГО Е

Будем повторять эту операцию для новых вершин. Теперь это можно сделать для вершины Е. В нее входит две «стрелки». Сумма чисел для предыдущих вершин равна 2 + 1 = З. Так постепенно получим результат для нужной нам вершины К.

             БО ДО            И                         БО ДО             и

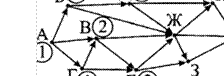  ГО ЕО 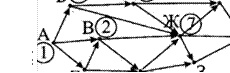ГО ЕО З

БО ДО

ГО ЕЭ

6.12. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой.

Сколько существует различных путей из города А в город К?

                                     Б        д            и

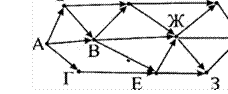
6.13. На рисунке схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

                                                    Б            д                  и

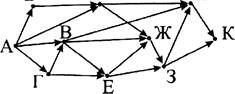
 7. ОПРЕДЕЛЕНИЕ ВЫИГРЫШНОЙ СТРАТЕГИИ ИГРЫ (АНАЛИЗ И ПОСТРОЕНИЕ ДЕРЕВА ИГРЫ)

Основные понятия

В третьей части экзамена выделяется одна задача, не связанная с программированием. На данный момент имеется два различных вида этих заданий. В первом случае предлагаются правила некоторой игры для двоих игроков. У каждого игрока имеется обычно 3—4 варианта хода. Нужно выяснить, кто выигрывает при безошибочной игре и как для этого он должен ходить.

При решении заданий данного типа предполагается, что вы проанализируете возможные ходы обоих игроков и определите, кто из них выигрывает и как он для этого должен ходить.

Сначала рассмотрим пример решения задачи (самый трудный из тех, что были предложены к настоящему моменту).

7.1. Два игрока, Петя и Ваня, играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй — З камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди, первый ход делает Петя. Ход состоит в том, что игрок или утраивает число камней в какой-то кучке, или добавляет 2 камня в какую-то кучку. Игра завершается в тот момент, когда количество камней в одной  из кучек становится не менее 19. Если в момент завершения игры общее число камней в двух кучках не менее 35, то выиграл Ваня, в противном случае — Петя. Кто выигрывает при безошибочной игре обоих игроков? Каким должен быть Йервый ход выигрывающего игрока? Ответ обоснуйте.

Самым универсальным способом решения задачи является, как ни странно, прямое решение — нужно последовательно, «уровень за уровнем» строить дерево игры. На первый взгляд эта идея выглядит угрожающе сложной (при 4-х вариантах хода, с каждым новым уровнем число рассматриваемых вариантов увеличивается в 4 раза; на 5-м ходу нужно рассматривать уже 45 = 1024 варианта). Не нужно этого заранее бояться. Нужно понимать, что задача составлена так, чтобы она имела разумное решение. А чтобы дерево не «росло» слишком быстро, нужно некоторые ветки отбрасывать, не рассматривая дальше. Это нужно делать в случае, когда дальнейшие ходы, очевидно, приводят к выигрышу одного из игроков.

Рассмотрим это решение. Для удобства построения дерева рекомендуем взять вертикально ориентированный лист бумаги и начать строить дерево не сверху вниз, как это принято, а слева направо. Эта рекомендация вызвана тем, что запись текущей позиции игры занимает много места по горизонтали, а рассматривать придется действительно много вариантов.

Договоримся, что текущее положение игры будем записывать двумя числами, через запятую — сначала число камней в первой кучке, потом — во второй. Так, исходную позицию в данном примере запишем как 4,3. Так как каждый игрок может для обеих кучек утроить число камней или добавить 2 камня, рассмотрим все 4 возможных хода первого игрока:

12, 3

4,6

Рисунок 7.1. Дерево игры. Варианты первого хода

Позиция 12,3 получилась после утроения числа камней в первой кучке, позиция 6,3 после добавления в первую кучку двух камней, позиция 4,9 — после утроения второй кучки, позиция 4,6 — после добавления во вторую кучку двух камней.

Теперь рассмотрим варианты хода второго игрока для каждой полученной позиции: 14,3

                                                                 14,3

Рисунок 7.2. Дерево игры. Варианты второго хода

Позиция 4,24 обведена прямоугольником, потому что в этой позиции игра заканчивается (во второй кучке больше 19 камней) проигрышем Вани (сумма камней в кучках менее 35).

Поэтому Ваня в эту позицию ходить не будет.


Позиция 36,3 обведена эллипсом, потому что в этой позиции игра заканчивается выигрышем Вани. Эго значит, что если Петя пойдет в 12,3, то Ваня выиграет ходом 36,3. Значит, позиция 12,3 является для Пети проигрышной и он туда ходить не будет. Обозначим эту позицию двойным прямоугольником. Очевидно, можно не рассматривать дальше ходы из позиции 12,3.

Интересно, что если бы мы заметили это раньше, можно было бы не рассматривать другие ходы из позиции 12,3.

Постараемся проанализировать, как еще можно сократить дерево ходов. Какие ходы нужно рассмотреть в первую очередь? Вероятно, те, про которые сразу будет что-то известно. Те, куда игрок обязательно пойдет, чтобы выиграть, и те, куда игрок ни в коем случае не пойдет, потому что проиграет.

Сейчас ход третий ход игры (ход Пети). Если сделать в одной кучке хотя бы 19 камней, игра закончится. Сначала посмотрим, получится ли при этом позиция, при которой сумма камней в кучках будет менее 35 камней (выигрыш Пети). Просматриваем варианты сверху вниз, например, см. рисунок 7.3.

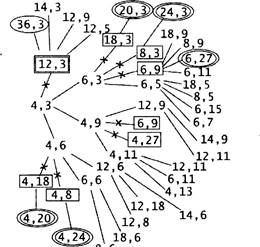
8,6

Рисунок 7.3. Дерево игры. Варианты третьего хода

Напоминаем, позиции после 12,3 (14,3 и 12,9 и 12,5) мы более не рассматриваем, потому что если Петя первым ходом пойдет в 12,3, Ваня пойдет обязательно в 36,3 и выиграет.

Следующая позиция — 18,3. Из нее можно закончить игру добавив 2 камня к 18-ти. При этом получится 20,3, это сразу приведет к выигрышу Пети. Значит, позиция 18,3 является выигрышной для Пети. Значит, Ване туда желательно не ходить. Очевидно, что остальные З варианта хода Пети из 18,3 можно не рассматривать (если есть один выигрышный ход, незачем рассматривать остальные).

Следующая позиция — 8,3. Если утроить 8 камней, получится 24,3. Это снова выигрыш Пети. Значит, и в позицию 8,3 Ване лучше не ходить.

Из позиции 6,9 игра закончится только ходом в 6,27. Сумма камней 33. Выигрыш Пети.

Значит, в позицию 6,9 Ване тоже лучше не ходить.

Из позиции 6,5 нет ни одного способа закончить игру. Рассматриваем все 4 варианта.

Из позиции 12,9 утроение любой кучки приводит к проигрышу Пети. Поэтому рассматриваем только добавление к кучкам двух камней.

Позицию 6,9 второй раз не рассматриваем — она такая же, как уже рассмотренная.

Из позиции 4,11 утроение второй кучки приводит к проигрышу Пети. Рассматриваем только остальные З варианта хода.

        Из позиции 12,6 — аналогично, не рассматриваем 36,6.         

Из позиции 6,6 рассматриваем только два хода — остальные два симметричны, не дадут ничего нового.

Из позиции 4,8 у Пети есть выигрышный ход в 4,24. Значит, в позицию 4,8 Ване лучше не ходить.

Аналогично, из позиции 4,18 у Пети есть выигрышный ход в 4,20. Значит, и в 4,18 Ване лучше не ходить. См. рис. 7.3.

Получившиеся позиции оцениваем с точки зрения хода Вани. Найдем позиции, из которых Ваня одним ходом выигрывает. Заметим, что 18,9 и 8,9 и 6,11 далее не рассматриваем, потому что Петя вместо них пойдет в 6,27 и выиграет.

Рассматриваем 4 варианта хода Пети из 6,5.

Из 18,5 и 6,15 Ваня утроит большую кучку и выиграет. Петя туда ходить не будет.

Ходы из 8,5 и из 6,7 рассмотрим все (два из них — 24,5 и 6,21 — сразу приводят к выигрышу Пети, далее их не будем рассматривать).

Рассмотрим варианты ходов Вани на ходы Пети из 12,9 и 4,11 и 12,6.

Очевидно, что Ваня может утроить ббльшую кучку в любой из этих позиций и выиграть. Значит, все эти позиции являются для Пети проигрышными. Значит, Ваня из 4,6 пойдет именно в 12,6 и остальные его ходы можно не рассматривать.

Получаем, что позиции 4,6 и 4,9 также является для Пети проигрышными (см. рис. 7.4).

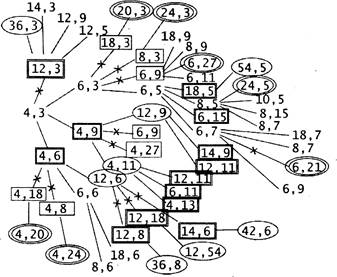
Рисунок 7.4. Дерево игры. Варианты четвертого хода

Осталось рассмотреть только 6 вариантов хода, полученных из позиций 6,7 и 8,5.

Из позиции 18,7 Петя может добавить 2 камня в первую кучку и выиграть (20,7).

Из позиции 8,7 Петя может утроить первую кучку и выиграть (24,7).

Позицию 6,9 мы уже рассматривали: Петя может утроить вторую кучку и выиграть (6,27).

Получается, что при любом ходе Вани из позиции 6,7 у Пети есть ответный выигрышный ход. Значит, позиция 6,7 является для Вани проигрышной. Отсюда делаем вывод, что предыдущая Петина позиция (6,5) выигрышная. Отсюда делаем вывод, что предыдущая позиция Вани проигрышная для него. Значит, из стартовой позиции Петя должен пойти именно в 6,3, чтобы выиграть.

Варианты хода Пети, полученных из позиции 8,5, теперь можно не рассматривать — мы уже нашли победителя.

Мы обозначили толстыми линиями те ходы, которые должен делать Петя, чтобы выиграть (см. рис. 7.5).

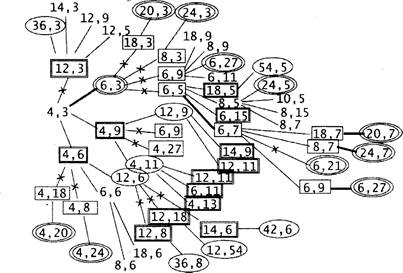
Рисунок 7.5. Дерево игры. Варианты пятого хода

 Заметим, что многие рассмотренные нами варианты хода оказались в результате ненужными оттого, что соседние с ними варианты приводили к победе. Вы можете попытаться найти для себя способ сразу «видеть» только те ветви дерева, которые нужны для решения. Нам представляется это излишним. На выписывание этих «лишних» вариантов уходит не так уж много времени, а потеря хотя бы одного критичного варианта чревата ошибкой всего решения.

Таким образом, мы решили задачу.

Как вы думаете, скојљко баллов (из трех возможных) мы заработали за это задание?


Надеемся, вы уже прочитали критерии оценивания этой задачи и поняли, что пока мы заработали ноль баллов. Если вы еще не прочитали критерии оценивания, внимательно прочитайте их сейчас:

Указания по оцениванию

Баллы

Правильное указание выигрывающего игрока и его ходов со строгим доказательством правильности (с помощью или без помощи дерева игры).

з

Правильное указание выигрывающего игрока, стратегии игры, приводящей к победе, но при отсутствии доказательства ее правильности.

2

При наличии в представленном решении одного из пунктов:

1.                Правильно указан выигрывающий игрок и его первый ход, рассмотрены все возможные ответы второго игрока, но неверно определены дальнейшие действия.

2.                Правильно указан выигрывающий игрок и его первый ход, но описание выигрышной стратегии неполно и рассмотрены несколько (больше одного, но не все) вариантов ответов второго игрока.

1

Задание не выполнено или в представленном решении полностью отсутствует описание элементов выигрышной стратегии и отсутствует анализ вариантов первого-второго ходов играющих (даже при наличии правильного указания выигрывающего игрока).

 

Мало решить задачу. Нужно еще правильным образом оформить ее решение и ответ.

Вы уже прочитали, что все три балла можно получить только в том случае, если приведено доказательство правильности выбранного решения.

Полученное нами дерево игры, с одной стороны, полностью отображает стратегию игры. С другой стороны, при нужном описании также можно будет считать доказательством правильности решения. Мы, однако, предлагаем только решать задачу таким способом, а вот ответ (и доказательство) записывать так, как это приведено в криТериях оценивания этой задачи, по которым вашу работу будут оценивать эксперты,

Это связано с тем, что у эксперта при проверке в образце задание будет оформлено именно так. И если вы приведете решение, полностью соответствующее этому образцу, у эксперта будет гораздо меньше сомнений, должен ли он ваш ответ засчитать как верное доказательство правильности. Он просто убедится, что вы слово в слово привели образцовый ответ и поставит вам ваши заслуженные З балла.

Рекомендуемый образец оформления ответа:

Выигрывает Петя, своим первым ходом он Должен Добавить 2 камня к первой кучке. Для Доказательства рассмотрим неполное Дерево игры, оформленное в виде таблицы, где в каждой ячейке записаны пары чисел, разделенные запятой. Эти числа соответствуют количеству камней на каждом этапе игры в первой и второй кучках соответственно.

 

Стартовая позиция

ход (Пети), выигрышный

II ход (Вани),

все варианты хода

III ход (Пети),

выигрышные ходы

IV ход (Вани), все варианты хода

V ход (Пети), выигрышные ходы

 

6,3

18,3

20,3

Выигрыш Пети

8,3

24,3

6,9

6,27

6,5

6,7

18,7

20,7

8,7

24,7

6,21

Выигрыш Пети

6,9

6,27

Таблица содержит все возможные варианты ходов второго игрока (Вани). Из нее видно, что при любом ответе второго игрока у первого (Пети) имеется ход, приводящий к победе.

Заметим, что приведенный образец оформления отчета обладает сразу тремя достоинствами:

во-первых, это самый короткий способ доказательства; во-вторых, он содержит в себе также и стратегию выигрышной игры Пети; в третьих (и это самое важное), именно такой способ оформления решения ожидают увидеть эксперты при проверке.

Обратите внимание! Мы рекомендуем выучить текст наизусть и привести именно эти фразы. В таблице обязательно подписать столбцы, указав для проигрывающего игрока «все варианты хода», а для выигрывающего игрока «ВЫИГРЫШНЫе ходы».

После таблицы ОБЯЗАТЕЛЬНО приведите эти две фразы, которые позволяют считать, что вы действительно доказали правильность решения.

Практическая часть

7.2. Два игрока, Петя и Ваня, играют в следующую игру. Перед ними лежат две кучки камней, в первой из которых 4, а во второй — З камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди, первый ход делает Петя. Ход состоит в том, что игрок или утраивает число камней в какой-то кучке, или добавляет 2 камня в какую-то кучку. Игра завершается в тот момент, когда количество камней в одной из кучек становится не менее 19. Если в момент завершения игры общее число камней в двух кучках не менее 33, то выиграл Ваня, в противном случае — Петя. Кто выигрывает при безошибочной игре обоих игроков? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

Ответ:

 

1-й ход

2-й ход

3-й ход

4-й ход

Стартовая позиция

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7.3. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 1 камень или удвоить количество камней в куче. Например, имея кучу из 7 камней, за один ход можно получить кучу из 8 или 14 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 30. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 30 или больше камней.

 В начальный момент в куче было S камней, 1 S 29.

Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он  должен сделать в любой ситуации, которая ему может встретиться при различной иг ре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

1.                а) При каких значениях числа S Петя может выиграть первым ходом? Укажите все такие значения.

б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрыш ную стратегию Вани.

2.                Укажите два значения S, при которых у Пети есть выигрышная стратегия, причем Петя не может, выиграть за один ход, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.

З. Укажите такое значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, но при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На ребрах дерева указывайте, кто делает ход, в узлах — количество камней в куче.

Решение и рекомендации по оформлению.

В этой задаче (к счастью) у Вас подробно, по пунктам, спрашивают ответ. Не ленитесь, так же подробно, по каждому пункту отвечайте развернуто и понятно.

Курсивом выделен образец ответа.

1а) Нужно найти такие значения S, при которых можно одним ходом выиграть. Очевидно, что проще всего выиграть ходом «удвоить количество камней». Найдем такие значения, удвоив которые можно сразу получить число 30 и больше. Это 30/2 = 15. Значит, при любых допустимых S 15 можно одним ходом выиграть. Образец оформления:

1а) При S = 15...29. Во всех этих случаях Петя Должен удвоить количество камней в куче и выиграть. При значениях S < 16 невозможно одним ходом (+1 или *2) получить больше 30 камней.

Обязательно укажите: диапазон верных значений, как нужно ходить, чтобы выиграть, а также почему для остальных S это не верно. Заметьте, что указание хода, который нужно сделать, является обязательным, несмотря на то, что этот ход (удвоить количество камней) очевиден, его нужно обязательно явно указать.

Также заметим, что для значения 29 не обязательно отдельно и дополнительно указывать, что выиграть можно также ходом «+1». Одного выигрышного хода более чем достаточно.

(Если Вы его укажете, это даже, скорее всего, немного расстроит эксперта, потому что, как указано в условии, «выигрышная стратегия» — это когда для каждой ситуации указан выигрышный ход. Один! Не нужно приводить все варианты выигрышных ходов.)

16) Нужно найти такое значение S, из которого, куда бы ни пошел, обязательно попадешь в диапазон, найденный в пункте 1а. Обычно это число, непосредственно на 1 меньшее, чем левая граница этого диапазона. В данном случае это 14. Образец оформления:

16) При S = 14. Куда бы ни пошел Петя (14 + 1 15 или 14*2 = 28), Ваня удвоит число камней в куче и выиграет (15*2 = 30, 28*2 = 56).

Обязательно укажите:

1)  верное значение,

2)  какие варианты хода Пети,

З) как должен ходить в ответ Ваня.

Не нужно указывать несколько вариантов-выигрышного хода, даже если они имеются. Указывайте только один. При этом тот, который совпадает с вариантом хода Вани при другом ходе Пети. Так проще, короче и понятнее.

2. Нужно рассмотреть «предыдущий ход» относительно позиции, указанной в пункте 16. То есть нужно указать такие позиции, из которых можно одним ходом получить число, указанное в пункте 16. В данном случае 14 можно получить, прибавив 1 к 13 или умножив на 2 число 7. Образец оформления:

2. S = 13 или S = 7. В обоих случаях Петя может получить в кучке 14 камней (13 + 1 — 14, 7*2 = 14). При любом ответном ходе Вани (14 + 1 15 или 14*2 = 28), Петя Должен удвоить число камней в куче и выиграть (15*2 = 30, 28*2 = 56

Несмотря на то, что с каждым следующти пунктом кажегся, что можно каждый раз ссылатыя на предыдущий пункт, при этом каждый раз меняется выигрывающий игрок. Позгому проще заново описать стратегию, чем потом оправдываться на апелляции, что Вы имели ввиду, когда пытајшсь сэкономить пару строк, а получили не очень понятный текст ответа. Поэтому повторяем еще раз.

Обязательно укажите:

1)       верные значения,

2)       для каждого из них: как должен ходить Петя (и сколько камней получится в куче), З) как может ходить в ответ Ваня (и сколько при этом будет в куче камней),  4) как должен в ответ ходить Петя.

З. Здесь нас просят снова рассмотреть «предыдущий ход» относительно позиции 2. То есть указать такую позицию, из которой куда бы ни ходил Петя, он либо попадет в диапазон пункта 1а (выигрыш Вани за 1 ход), либо попадет в одну из позиций пункта 2 (выигрыш Вани за 2 хода). Рекомендуем рассмотреть такие позиции, из которых можно получить за один ход позиции из пункта 2.

В данном случае, так как возможные ходы «+1» или «*2», а в пункте 2 оба числа (7 и 13) нечефные, достаточно рассмотреть числа 6 и 12 (6 + 1 7 И 12 13). В обоих случаях рекомендуем построить дерево возможных ходов и в одном из них убедиться, что Ваня выигрывает за 1 или за 2 хода. Его и записать в ответ.

В данном случае при S = 6 Петя может ходить в 7 или в 12, и Ваня ни в одной из этих позиций не может выиграть в один ход (как требуется по условию). Поэтому можно сразу рассматривать S = 12. Строим дерево: в:*2 15 в:*2 12       28

Убеждаемся, что все получается так, как нужно, и записываем ответ:

З) S — 12. Если Петя удвоит число камней в куче (12*2 = 24), Ваня тоже Должен удвоить число камней в куче и выиграть. Если Петя Добавит 1 камень в кучу (12 + 1 ¯ 13),

Ваня также Должен Добавить 1 камень в кучу (13 + 1         14 )•

В ответ на любой следующий ход Пети (14 + 1 15 или 14*2 = 28) Ваня Должен удвоить число камней в куче и выиграть (15*2 = 30, 28*2 = 56). Рассмотрим Дерево игры:

В : +10 В этом Дереве в каждой позиции, где дол19 В:+1 жен ходить Петя, разобраны все возмож18 в:+10ные ходы, а для позиций, где Должен ходить п:чо 28—•

Ваня     только ход, соответствующий стратегии, которую выбрал Ваня.

Обратите внимание на то, что рекомендуется здесь написать:

1)    опишите словами стратегию выигрыша Вани,

2)    нарисуйте дерево игры. На ребрах дерева указывайте, кто сейчас ходит и как,

З) обязательно приведите фразу, указанную после дерева («В этом Дереве...»). Выучите этот текст и напишите его в чистовик при оформлении этой задачи. Без этого текста Вам могут не зачесть правильное решение пункта З.

7.4. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 1 камень или 10 камней. Например, имея кучу из 7 камней, за один ход можно получить кучу из 8 или 17 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 31. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 31 или больше камней. В начальный момент в куче было S камней, 1 S 30.

Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

1.                а) При каких значениях числа S Петя может выиграть первым ходом? Укажите все такие значения.

б) Укаэките такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

2.                Укажите два значения S, при которых у Пети есть выигрышная стратегия, причем Петя не может выиграть за один ход, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня, Для указанных значений S опишите выигрышную стратегию Пети.

З. Укажите такое значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, но при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или табли цы). На ребрах дерева указывайте, кто делает ход, в узлах — количество камней в куче.

7.5. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырех позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 55. Победителем считается игрок, сделавший последний ход, то есть первым получивший такую позицию, что в кучах всего будет 55 или больше камней.

В начаљный момент в первой куче было 5 камней, во второй куче — S камней; 1 S 49.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

Задание 1

а) Укажите все такие значения числа S, при которых Петя может выиграть за один ход, и соответствующие выигрывающие ходы. Если при некотором значении S Петя может выиграть несколькими способами, достаточно указать один выигрывающий ход.

б) Сколько существует значений S, при которых Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом?

Задание 2

Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

 Петя не может выиграть за один ход;

 Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанного значения S опишите выигрышную стратегию Пети.

Задание З

Укажите значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани.

Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На ребрах дерева указывайте ходы, в узлах указывайте позиции.

В заданиях 2 и З достаточно указать одно значение S и объяснить, почему это значение удовлетворяет условию соответствующего задания.

Решение и рекомендации по оформлению.

1а. В первой куче 5 камней. Выигрыш при 55 камнях. Значит, во второй куче нужно получить 50 и более камней. Ходом удвоения можно получить 50 и более камней, имея во второй куче хотя бы 25 камней (25 • 2 = 50). Значит, наш ответ: S = 25...49. Петя Должен удвоить число камней во второй куче.

16. Единственный вариант, который может нас устроить, S = 24. Проверим его.

Из позиции (5, 24) можно получить позиции (6, 24), (10, 24), (5, 25), (5, 48). Среди этих позиций из позиции (6, 24) нельзя выиграть одним ходом (самый «максимальный» по сумме камней ход 24 • 2 даст всего лишь (6, 48) = 54 камня в двух кучах). Значит, этот вариант S = 24 не подходит. При S < 24 очевидно, что существуют ходы, прибавляющие 1 ко второй куче, которые приводят нас последовательно к случаям, которые не подходят. Значит, ответ на вопрос 16 — О (нет таких S). Рекомендуем привести в ответе доказательство правильности этого ответа. Например, так:

Единственный подходящий вариант (S = 24) не подходит, так как при первом ходе Пети «+1 к первой куче» получается ситуация (6, 24), из которой нельзя выиграть одним ходом. Числа, меньшие 24, тоже не подходят (при S = 23 Добавление 1 камня во вторую кучу приводит к (5, 24), из которой не выиграть). Аналогично, можно такое показать для каждого меньшего S.

2. Только что рассмотренный случай S = 24 приводит нас к ответу на это задание. Мы заметили, что ситуация (6, 24) е является выигрышной. Проверим, проигрышная ли она. Рассмотрим, как может походить игрок из позиции (6, 24). Это позиции (7, 24), (12, 24), (6, 25), (6,48). Легко видно, что во всех этих случаях удвоение второй кучи дает в сумме в кучах не менее 55 камней. То есть, позиция (6, 24) проигрышная. Значит, именно в нее нужно стараться «загнать» соперника. Ответ:

S = 24. Первым ходом Петя Должен Добавить 1 камень в первую кучу (получится (6, 24)). При любом ответном ходе Вани Петя Должен удвоить вторую кучу и выиграть.

З. Воспользуемся выводами, сделанными нами в задании 2. Позиция (5, 24) является выигрышной, а позиция (6, 24) проигрышной. Из какой позиции, куда бы ни походил игрок, он попадет в позицию (5, 24)? Например, из (5, 23). Проверим эту позицию.

Из (5,23) одним ходом можно попасть в позиции (6, 23), (5, 24), (10, 23) и (5, 46). Из позиций (6, 23) и (5, 24) можно одним ходом (+1) получить позицию (6, 24), которую мы уже определили как проигрышную.

А из позиций (10, 23) и (5, 46) можно одним ходом выиграть, удвоив число камней во второй куче.

Значит, наше предположение верно. Осталось только оформить ответ: S - 23.

Рассмотрим Дерево игры:

в: 24*2

(5 , 23)

В Дереве рассмотрены все возможные ходы Пети и ответные ходы Вани, соответствующие выигрышной стратегии. Знаком «>>» обозначены позиции, в которых партия заканчивается.

7.6. Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырех позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.

Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 55. Победителем считается игрок, сделавший последний ход, то есть первым получивший такую позицию, что в кучах всего будет 65 или больше камней.

В начальный момент в первой куче было 7 камней, во второй куче — S камней; 1 S 57. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть  при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

Задание 1

а) Укажите все такие значения числа S, при которых Петя может выиграть за один ход, и соответствующие выигрывающие ходы. Если при некотором значении S Петя может выиграть несколькими способами, достаточно указать один выигрывающий ход.

б) Сколько существует значений S, при которых Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом?

Задание 2

Укажите такое значение S, при котором у Пети есть выигрышная стратегия, причем одновременно выполняются два условия:

— Петя не может выиграть за один ход;

 Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанного значения S опишите выигрышную стратегию Пети.

                   Задание З       

Укажите значение S, при котором одновременно выполняются два условия:

— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети;

— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.

Для указанного значения S опишите выигрышную стратегию Вани.

Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На ребрах дерева указывайте ходы, в узлах указывайте позиции.

В заданиях 2 и З достаточно указать одно значение S и объяснить, почему это значение удовлетворяет условию соответствующего задания.

7.7. Два игрока, Паша и Витя, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырех позиций: (11, 7), (20, 7), (10, 8), (10, 14), Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 47. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 47 или больше камней.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. Например, при начальных позициях (З, 22) и (1, 23) выигрышная стратегия есть у Паши. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.

Задание 1. Для каждой из начальных позиций (6, 20), (8, 19) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание 2. Для каждой йз начальных позиций (5, 20), (7, 19), (8, 18) укажите, кто из игроков имеет выигрышную стратегию. В каждОм случае опишите выигрышную стратегию; объясните, почему эта стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание З. Для начальной позиции (7, 18) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.

Решение и рекомендации по оформлению.

Решаем задания по порядку, начиная с первого.

Задание 1.

Проанализируем начальные позиции первого задания.

 Из позиции (6,20) можно получить (7,20), (12,20), (6,21 ), (6,40). Во всех случаях сумма камней в кучах меньше 47, однако удвоение второй кучи приводит к выигрышу (в сумме будет не менее 47 камней). Значит, позиция (6,20) проигрышная и выигрышную стратегию имеет Витя. Он выигрывает своим первым ходом.

Из позиции (8,19) можно получить (9,19), (16,19), (8,20), (8,38). Во всех этих случаях сумма камней в кучах также меньше 47 и удвоение второй кучи приводит к выигрышу. Значит, позиция (8,19) — также проигрышная и ВЫИГРЫШНУЮ стратегию имеет Витя. Он выигрывает своим первым ходом.

Что нужно записать в ответ?

Нас просят указать сразу 4 вещи для каждой из 2-х позиций (то есть всего 8):

1)   указать, кто из игроков имеет выигрышную стратегию,

2)   описать выигрышную стратегию,

З) объяснить (доказать), почему эта стратегия ведет к выигрышу,

4) указать, какое наибольшее число ходов может потребоваться победителю.

Чтобы ответ был засчитан как доказательство, нужно обязательно привести все возможные ходы проигрывающего игрока (и позиции, в которых окажется игра в этот момент) и в каждом случае указать, как должен походить выигрывающий игрок.

Например, можно оформить ответ так, как указано выше курсивом.

       Задание 2.         

Желательно воспользоваться тем результатом, который мы получили при решении задания 1.

А именно тем, что позиции (6,20) и (8,19) — проигрышные.

Нетрудно видеть, что из позиций задания 2 можно легко одним ходом получить позиции задания 1. Значит, они — выигрышные. Запишем ответ:

Для каждой из рассматриваемых позиций существует ход, который приводит в проигрышные позиции, рассмотренные в задании 1.

     (5,20)     (6,20), (7,19)       (8,19), (8,18) (8,19).

Значит, эти позиции — выигрышные. Выигрышную стратегию имеет Паша. Его первый ход нами указан. Паша выигрывает на своем втором ходу. Игра из позиций (6,20) и (8,19) рассмотрена в задании 1.

Задание З.

Рассматриваем указанную позицию (7,18). Из нее можно получить позиции (8,18), (7,19), (14,18), (7,36). Позиции (8,18) и (7,19) рассмотрены в задании 2 как выигрышные.

Позиции (14,18) и (7,36) выигрышные, потому что в них удвоение второй кучи дает в кучах более 47 камней.

Запишем ответ:

В позиции (7,18) выигрышную стратегию имеет Витя. Если Паша первым ходом пойдет в (8,18) или (7,19), Витя пойдет в (8,19) и выиграет своим вторым ходом. Стратегия его игры описана в заданиях 1 и 2.

Если же Паша первым ходом пойдет в (14,18) или (7,36), Витя выиграет своим вторым ходом, удвоив количество камней во второй куче.

Рассмотрим Дерево игры:

в • 19*2 в: 18+1

(7 , 18)

В этом Дереве рассмотрены все возможные ходы Паши и соответствующие им ходы Вити -согласно выигрышной стратегии. Знаком >> обозначены позиции, в которых партия заканчивается.

7.8. Два игрока, Паша и Витя, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Паша. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырех позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 63. Победителем считается игрок, сделавший последни1 ход, т.е. первым получивший такую позицию, что в кучах всего будет 63 или больше камней.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной  игре противника. Например, при начальных позициях (З, 30) и (1; 31) выигрышная стратегия есть у Паши. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.

Задание 1. Для каждой из начальных позиций (10, 26), (12, 25) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

 Задание 2. Для каждой из начальных позиций (6, 25), (9, 26), (10, 25) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание З. Для начальной позиции (9,25) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта Стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.

8. ФАЙЛОВАЯ СИСТЕМА КОМПЬЮТЕРА

Основные понятия

Для удобства использования данные на компьютере хранятся в виде файлов. Файлом называется поименованная совокупность данных, хранящихся на внутреннем (жесткий диск, флэш-диск) или внешнем  дискета, флэш-карта, карта памяти, магнитная лента и др.) носителе информации.

Имя файла обычно состоит из собственно имени и так называемого расширения, служащего для определения типа данных, хранящихся в файле (типа файла). Имя файла и его расширение разделяются точкой.

Кроме имени, файл обычно имеет атрибуты (дата создания, дата изменения, пользователь, права доступа и т.д.).

Файловая система позволяет организовывать файлы в иерархические древовидные каталоеи. Каталог самого верхнего уровня называется корневым каталогом. Во многих операционных системах (в том числе семейства Windows) корневой каталог обозначается именем логического источника данных — латинской буквой с двоеточием. Буквы А и В обозначают дисководы для дискет, С — жесткий диск компьютера, остальные буквы — внутренние носители данных или внешние, подключейные к компьютеру, например по интерфейсу USB или по сети.

Остальные каталоги делятся на системные и пользовательские. Системные каталоги имеют служебные имена, назначенные операционной системой при установке. Имена пользовательских каталогов задаются пользователем по его усмотрению.

Пользователь может передвигаться по каталогам с помощью программ навигации (Проводник, FarManager и др.) или с помощью специальных команд операционной системы. Тот каталог, в котором пользователь находится в настоящий момент, называется текущим каталоеож.

Последовательность имен каталогов, проходимых от некоторого каталога до нужного файла, называется путем к этому файлу. Имена каталогов в этой последовательности принято разделять знаком «Х».

Различают абсолютное (полное) и относительное имя файла. Абсолютное имя складывается из пути к файлу от корневого каталога и имени файла. Относительное имя из пути к файлу из текущего каталога и имени файла. Если файл находится в текущем каталоге, то его относительное имя есть просто имя файла.

Пример. Пусть имя файла

Это полное (абсолютное) имя файла, поскольку оно начинается с имени корневого каталога Е:. Путь к файлу — E:\SCHOOL\USER\DOC\. Само имя файла — user.txt, где txt расширение, указывающее на то, что файл должен содержать текстовые данные.

Для групповых операций с файлами (поиск, удаление, перемещение) используются маски имен файлов. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы: символ «?» (вопросительный знак) означает ровно один произвольный символ;  символ « * » (звездочка) означает любую последовательность символов произвольной длины, в том числе « * » может задавать и пустую последовательность.

Примеры.

Маска для выделения всех файлов в текущем каталоге: * . *

Маска для выделения файлов с расширением .txt: * .txt

Маска для выделения файлов, имена которых начинаются с буквы s и имеют односимвольное расширение: s * .

Практическая часть

8.1. Выпишите имя корневого каталога, путь файлу, его расширение:

а)

Ответ:

6)

Ответ: в)       С:\Мои документы\фото\2ОО7\портрет.јрд

Ответ: г)

Ответ:

8.2. На рисунке приведен фрагмент файловой системы компьютера.

В Новый том (I:)

В Flash

В б] ActionScript 2.0. ДЛЯ профессионалов

В Проекты Глава з глава 4 Е Глава 5 в глава 6

100х100

GlF JPEG kmol round

Глава 7 Глава 8

В глава 9 глава 10

а)         Запишите полный путь к файлу 333.gif, находящемуся в каталоге GIF.

Ответ: б)       Запишите путь из каталога Проекты к файлу 333.gif, находящемуся в каталоге GIF.

Ответ:

в)          Запишите путь из каталога Глава 6 к файлу 333.gif, находящемуся в каталоге GIF.

Ответ:

г)          Запишите полный путь к файлу test.swf, находящемуся в каталоге Проекты.

Ответ:

Пример. Какие файлы будут выбраны из текущего каталога по маске d * с.?р

Решение.

По указанной маске будут выбраны из текущего каталога все файлы, имена которых начинаются на d и заканчиваются на с и одновременно имеют двухбуквенное расширение, заканчивающееся на р.

Пример. Составьте маску, по которой из текущего каталога будут выбраны все файлы, имена которых начинаются на букву «F» с расширением, состоящим ровно из трех символов.

Решение.

Составим отдельно маски для расширения и собственно имени файла.

Поскольку указано, что расширение состоит ровно из трех символов, для него необходимо использовать маску «???». Символ «* » в данном случае использовать нельзя, так как он не накладывает ограничений на длину подставляемой последовательности символов. Напротив, поскольку для имени файла ограничения на длину не предусмотрены — маска для имени будет «F * ».

Объединяя маски для имени и расширения и не забывая про разделитель имени и расширения — точку, получаем ответ: F * .???

Пример. Определите, какое из указанных имен файлов удовлетворяет маске ?cr * m.d?c 1) crim.doc 2) acrims.doc З) ocrm.dtc 4) ocrm.dc Решение.

Проверим последовательно, какие имена файлов удовлетворяют указанной маске:

1)    crim.doc  не подходит, так как символу «?» в имени файла ничего не соответствует, а

это недопустимо;

2)    acrims.doc не подходит, поскольку в имени файла есть лишний символ «s», не соответствующий маске;

З) ocrm.dtc подходит, символу «?» маски в имени файла соответствует ровно одна буква «о», а в расширении «t». Символу « * » маски в имени файла соответствует пустая последовательность символов, что допускается.

Для полноты решения проверим четвертый вариант.

4) ocrm.dc — не подходит, так как символу «?» в расширении файла ничто не соответствует,

что недопустимо. Ответ: З.

8.3. В текущем каталоге имеются файлы: 1) zzz.cpp 2) zzz.cpppc З) z.c

                                                                                                                       4) 1.срр               5) 123.рс

а)         Какие файлы будут выбраны из текущего каталога по маске * .срр

Ответ: б)       Какие файлы будут выбраны из текущего каталога по маске ?.срр

Ответ: в)       Какие файлы будут выбраны из текущего каталога по маске * z * .с?р

Ответ: г)       Какие файлы будут выбраны из текущего каталога по маске * . * с

Ответ:

8.4.

а) Составьте маску, по которой из текущего каталога будут выбраны все файлы с расширением .doc, в именах которых встречается буква «я».

Ответ:

6) Составьте маску, по которой из текущего каталога будут выбраны все файлы с расширением .doc, имена которых начинаются и заканчиваются на букву «я».

Ответ:

в) Составьте маску, по которой из текущего каталога будут выбраны все файлы, имена которых начинаются на букву «z» с расширением, состоящим ровно из двух символов.

Ответ:

г) Составьте маску, по которой из текущего каталога будут выбраны все файлы с расширением .txt, имена которых включают идущие подряд цифры 2009.

Ответ:

Пример. В каталоге находится 5 файлов: boom.pas bloom.ppt loom.pas bottom.pdf bom.pps

Определите, по какой из масок будет выбрана указанная группа файлов:

boom.pas bloom.ppt bottom.pdf

              1) ?оо*т.р*                    2) Ь*от.р?*                     З) *о*от.р*?                    4) Ь*о*от.р??

Решение.

Найдем имена исходных файлов, которые не были отобраны по маске: loom.pas, bom.pps. Проверим последовательно каждую маску на то, чтобы все выбранные файлы ей удовлетворяли, а при этом невыбранные файлы ей не удовлетворяли:

1)   ?оо*т.р* — не подходит, так как символ «?» в начале имени файла требует, чтобы перед «оо» находился ровно один символ, а этому условию не удовлетворяет выбранный файл bloom.ppt;

2)   Ь*от.р?* — не подходит, поскольку этой маске удовлетворяет не только выбранные файлы, но и файл bom.pps, который не должен быть отобран; не подходит, поскольку этой маске удовлетворяет не только выбранные файлы, но и файл loom.pas, который не доджен быть отобран.

Для полноты решения проверим четвертый вариант.

4) Ь*о*от.р?? подходит, все отобранные файлы соответствуют этой маске; loom.pas ей не соответствует, потому что его первая буква «1», а маска требует «Ь»; bom.pps ей не соответствует, потому что в нем только одна буква «о», а маска требует двух. Ответ: 4.

Задания формата ЕГЭ

8.5.

а) В некотором каталоге хранился файл  После того как в этом каталоге создали подкаталог и переместили в созданный подкаталог файл  полное имя файла стало Каково имя вновь созданного каталога?

            1) Поэты                                                  3) XIX                              4) Россия

6) В некотором каталоге хранился файл  После того как в этом каталоге создали подкаталог и переместили в созданный подкаталог файл  полное имя файла стало Каково имя вновь созданного каталога?

            1) Алгебра                      2) Математика                                                              4)

в) Перемещаясь из одного каталога в другой, пользователь последовательно посетил каталоги Задачи, 9, Алгебра, С:\, Геометрия, 11. Каково полное имя каталога, в котором оказался пользователь?

Примечание: при каждом перемещении пользователь либо спускался в каталог на уровень ниже, либо поднимался на уровень выше.

1)     11  З) С:\Геометрия\11

2)     С:\ Алгебра\9\Задачи  4) Геометрия 11

г) Перемещаясь из одного каталога в другой, пользователь последовательно посетил каталоги Задачи, Геометрия, В:\, Алгебра, Уравнения, Задачи. Каково полное имя каталога, в котором оказался пользователь?

Примечание: при каждом перемещении пользователь либо спускался в каталог на уровень ниже, либо поднимался на уровень выше.

1) Алгебра\Уравнения\Задачи

З) В:\Геометрия\Задачи

2) В:\ Алгебра\Уравнения\Задачи

4) Геометрия\Задачи

8.6.

а)        Определите, какое из указанных имен файлов удовлетворяет маске: hel?lo.c??

             1) hello.cpp                     2) helolo.c                        З) helolo.cnt                    4) helsslo.cpp

           б)        Определите, какое из указанных имен файлов удовлетворяет маске: he * о.с *

             1) helol.cpp                     2) he.oc                            З) helolo.pcc

в)       Определите, какое из указанных имен файлов удовлетворяет маске:

            1) com.doc                       2) dcoma.dc                     З) dcom.dotc

г)        Определите, какое из указанных имен файлов удовлетворяет маске:

            1) com.doc                       2) dcoma.dc                     З) dcom.dotc

8.7.

а)        Укажите, какой маске удовлетворяют следующие файлы: com.doc dcoma.doc dcom.dotc dcoma.cdc

1) *com?.d*

б)        Укажите, какой маске удовлетворяют следующие файлы:

123.tex

12.txt

1234.tex

123.txt

в)        Укажите, какой маске удовлетворяют следующие файлы:

abc.txt abd.tif abcd.txt abc.tif

г)  Укажите, какой маске удовлетворяют следующие файлы: xyz.hlp xyt.htm xyz.htm xtz.hlp

1) ху*.???

8.8.

а)       Некий файл хранится по следующему адресу:

Укажите заведомо неверное утверждение.

4) herro.c

.com * .d?c

4) dcoma.djc

* com?.d * с 4) dcoma.cdc

4) 12*.t??

4) x*z.h*

1)    Из папки VASYA путь к файлу моэкно указать так: PICTURES\FACE.JPG

2)    Этот файл содержит изображение черного треугольника на синем фоне

                3) IIOJIHOe 0Toro     FACE.JPG

                     4) 3TOT   xpaHMTCfl He B KOPHe AMCKa D:

              6)      Hexni       xpaHwrca no cJ1eAYK)1.ueMY mxpecy:

YKaycvne gaBeA0M0 HeBepHoe Y'1'BepxqeHne.

1) 110JIHoe

2) Tax: HOMEWORK\WINTER.DO 3) 3TOT    xpaHHTca B K0PHe AncKa A:

                     4) 3TOT comepxcwr rra6JIH11Y pacnmcaHHfl noe3AOB

              B) OnpeAeJIHTe, I-car-coe YKa3aHHb1X uraeH YÅ0BJ1eTBopqerr MacKe.• ??prive * t.p? *

1) Aprivet.pas 2) zlprivet.past

3) privert.p3

4) doprivest.p

                r) OnpeAeJIHTe, I-caKoe H3 YKa3aHHb1X nrvreH d)aiJIOB YAOBJ1eTBOPfleT Macr-ce: ?info * rm.d * ?

1) 12inf07rm.deep

2) Ilinform.doc

3) 4inf05rm.d 4) 7inform.dp

8.9.

a) B KaTaJ10re Haxomwrca 5 sound.tif son. txt spoon.ttf slon. tif pound.txt

                OnpemeJIHTe, no I-caK0ii MaCOK 6YAeT Bb16paHa YKa3aHHaa rpynna d)aiiJ10B:

son.txt spoon.ttf slon.tif

                                                           2) s*n.t??

6) B KaTa.more HaXOAMTCfl 5 sound. tif son.txt sun.ttf slon.tif  pound. txt

OnpeAeJIHTe, 110 1-caKOÜ H3 MaCOK 6yzxeT Bb16paHa YKaaaHHaq rpynna son.txt

sun.ttf         pound.txt

в)       В каталоге находится 5 файлов: sound.tif son.txt sun.ttf  slon.tif pound.txt

Определите, по какой из масок будет выбрана указанная группа файлов: sound.tif sun.ttf pound.txt

4) ?*n*.*t*

г)         В каталоге находится 5 файлов: sound.tif son.txt spoon.ttf       slon.tif pound.txt

Определите, по какой из масок будет выбрана указанная группа файлов: sound.tif spoon.ttf slon.tif

9. ЭЛЕКТРОННЫЕ ТАБЛИЦЫ

Основные понятия

Так как одним из самых удобных способов представления информации является таблица, обработке таблиц посвящена отдельная категория программных продуктов — электронные таблицы. Электронная таблица состоит из строк и столбцов, на пересечении которых находятся ячейки. Каждая ячейка может хранить один из нескольких видов информации: текстовую, числовую, дату/время или формулу.

В электронных таблицах принято обозначать столбцы буквами латинского алфавита, а строки — числами. Таким образом, для обозначения ячейки нужно указать номер столбца и номер строки этой ячейки. Например, D7. Это называется адресом ячейки.

Для обработки информации, содержащейся в ячейках, используют формулы.

Формулы в электронных таблицах начинаются с символа равно (=). В качестве аргументов в формулах можно использовать числа, элементы текста и адреса других ячеек. Эти аргументы можно связывать различными алгебраическими операциями, операциями отношения и другими.

Для удобства в электронных таблицах введены различные функции. Самые широкоиспользуемые — вычисление суммы (СУММ) и вычисление среднего арифметического значения (СРЗНАЧ).

Для перечисления адресов ячеек, над которыми должна быть осуществлена функция, используют знак «;» (точка с запятой). Для указания прямоугольного блока ячеек используется обозначение Диапазона: адрес верхней левой и правой нижней ячеек блока, с символом «:» (двоеточие) между ними.

При копировании формул из одной ячейки в другую действует автоиндексация. Это значит, что адреса ячеек при копировании будут изменены в соответствии с расстоянием, на которое осуществляется копирование. То есть если копируется формула из ячейки на З столбца вправо и на 2 строки вверх, то во всех адресах, которые присутствуют в формуле, номера столбцов будут «увеличены» на З, а номера строк уменьшены на 2.

Чтобы такого эффекта не происходило, перед теми элементами адреса (номером столбца и/или номером строки), которые не должны измениться при копировании, нужно ставить знак доллара ($). Это называется абсолютная адресация ячейки. В противоположность ей, отсутствие знака доллара в адресе называется относительной адресацией.

Практическая часть

9.1. Укажите одно или несколько правильных утверждений. Буквы, соответствующие правильным утверждениям, обведите, остальные — зачеркните.

Для электронных таблиц справедливо:

а) электронная таблица состоит из строк и столбцов, на пересечениях которых находятся ячейки;

б) строки и столбцы электронной таблицы пронумерованы. Строки обычно нумеруются последовательными натуральными числами. Столбцы обычно нумеруются буквами латинского алфавита, от А и дальше;

в) каждая ячейка электронной таблицы имеет уникальный адрес, состоящий из номера столбца и номера строки (например, А1, С14, BD23).

9.2. Укажите один или несколько правильных ответов. Буквы, соответствующие правильным ответам, обведите, остальные — зачеркните.

Какая информация может храниться в ячейке электронной таблицы?

а) Целое число

д) Время/дата

б) Вещественное число

е) Звук

в) Графическое изображение

ж) Вложенная таблица

г) Строка символов

з) Формула

9.3. Для расчета значения ячейки на основании значения другой ячейки (ячеек) в электронных таблицах используются формулы. Укажите выражения, которые электронная таблица будет считать формулами и вычислит. Буквы, соответствующие правильным ответам, обведите, остальные — зачеркните:

                        б)                                                                                  ж) А1 + АЗ

и) = Щ 12 + 4)

              д) - 53 - 10                                          

9.4. Для осуществления операций над константами и значениями ячеек в электронной таблице используются операторы. Сопоставьте каждому оператору (слева) действие, которое этот оператор осуществляет (справа). Впишите рядом с буквой операции число, соответствующее смыслу этой операции:

 

1) возведение в степень (первый аргумент в степени второго)

6)

2) сравнение аргументов (если первый меньше или равен второму)

З) сравнение аргументов (если первый больше второго)

г)

4) сложение аргументов

д)

5) умножение аргументов

е)

6) деление первого аргумента на второй

7)     сравнение аргументов (если первый больше или равен второму)

8)     сравнение аргументов (если аргументы не равны)        

9)     вычитание второго аргумента из первого

10)склеивдние двух текстовых аргументов

11)сравнение аргументов (если аргументы равны)

9.5. Для осуществления более сложных действий над аргументами в электронных таблицах используются функции. Укажите, какие из приведенных утверждений верны при записи функций (в электронной таблице). Буквы, соответствующие правильным утверждениям, обведите, остальные — зачеркните:

а) функции используются в формулах (то есть в выраэкениях, начинающихся со знака — (равно));

б) каждая функция имеет свое уникальное имя;

в) имя функции должно быть записано обязательно русскими буквами;

г) после указания имени функции нужно обязательно написать аргументы в круглых скобках;

д) даже если функция не имеет аргументов, все равно нужно написать пустые круглые скобки;

е) аргументы функции отделяются друг от друга символом «;» (точка с запятой);

ж) для указания в качестве аргумента целой области соседних ячеек используется Диапазон ячеек;

з) прямоугольный диапазон ячеек записывается указанием адреса левой верхней и правой нижней ячейки прямоугольного диапазона через символ (двоеточие). Например, А1:ВЗ;

и) для указания в качестве диапазона целиком строки, столбца или нескоЛьких используется только один (нужный) индекс. Например: А:А (весь столбец А); B:D (столбцы от В до D); 6:6 (вся строка 6); 4:12 (строки начиная с 4-й по 12-ю).

9.6. В списке наиболее часто используемых функций установите соответствие между именем функции и возвращаемым ею значением. Впишите рядом с буквой функции чисЛО, соответствующее смыслу этой функции:

                         а) СУММ                      1) наибольшее значение

2) если указанное условие ИСТИНА, то второй аргумент, ина-

6) СРЗНАЧ че — третий аргумент

                         в) МАКС                      З) наименьшее значение

                           г) мин                           4) сумма

                         д) ЕСЛИ                      5) среднее арифметическое (сумма, деленная на количество)

9.7. Во всех ячейках таблицы записано число 1. Вычислите результат функции СУММ для каждого списка аргументов:

з) СУММ(З:З) -

9.8. Для данной электронной таблицы вычислите результат функций:

 

опт

1

з

5

 

 

 

 

 

 

 

 

 

9.9. В электронной таблице значение формулы :В2) равно 5. Чему равно значе-

ние ячейки ВЗ, если значение формулы =СРЗНАЧ(В1:ВЗ) равно З?

Рекомендация. Нарисуйте на черновике (или представьте) упоминаемые в задаче ячейки. Вспомните, что символ «:» (двоеточие) между адресами ячеек — это не перечисление, а указание на диапазон. Вспомните, что СРЗНАЧ — это не «сложить и поделить пополам», а сумма указанных ячеек, деленная на их количество. А количество в данном случае вовсе не две. Догадайтесь, что если мы знаем количество и среднее значение, то можно отсюда вычислить сумму. Осталось догадаться, что если известна сумма N чисел и сумма тех же чисел, но без одного из них, то вычитанием легко вычислить оставшееся число.

9.10. В электронной таблице значение формулыравно 5. чему равно значение ячейки D1, если значение формулыравно 7?

9.11. В электронной таблице значение формулыравно 4. Чему равно значение ячейки А1, если значение формулыравно 9?

9.12. В электронной таблице значение формулы =СРЗНАЧ(А1:В4) равно З. Чему равно значение ячейки А4, если значение формулы =СУММ(А1:ВЗ) равно 30, а в ячейке В4 лежит 5?

Ответ:

Напоминание. Обычная запись адреса ячейки в формуле (например, С5) соответствует относительной адресации ячейки. Это значит, что при копировании такой формулы в другую ячейку таблицы произойдет автоматическая индексация. То есть обе части адреса ячейки (номер строки и номер столбца, они называются индексами) изменятся на такое значение, на сколько по вертикали и по горизонтали ячейка была скопирована относительно своего исходного положения. Например, формула «=С5» находится в ячейке А4. Эта формула копируется в ячейку В2 2 строки выше и на один столбец правее. То есть новый адрес формулы уменьшается на 2 по вертикали (номер строки) и увеличивается на один по горизонтали (номер столбца). Значит, относительные адреса ячеек, используемых в формуле, изменяются на эти же величины: номер строки уменьшается на 2, номер столбца увеличивается на 1. Адрес С5 превратится в адрес 03 (С + 1, 5 - 2).

9.1 За Дан фрагмент электронной таблицы:

 

 

в

с

1

1

з

=А1+В1+2

2

2

4

 

                     Чему станет равным значение ячейки С2, если в нее скопировать формулу из ячейки С1?

Ответ:

Напоминание. Если при копировании формулы не требуется автоматическая индексация, используют абсолютную адресацию ячеек. для этого перед той частью адреса (перед тем индек сом), которая не должна измениться при копировании, нужно поставить знак доллара ($). Если знак абсолютной адресации стоит перед обеими частями адреса (обоими индексами, например $С$5), этот адрес не изменится при копировании в любое место. Если знак «$» только перед одной частью адреса — будет изменяться та часть адреса (тот индекс), перед которым знак доллара не стоит. Например, адрес $В4 не будет меняться при копировании влево-вправо, но будет меняться (как обычно) при копировании вверх-вниз.

9.14. Дан фрагмент электронной таблицы:

 

 

в

с

1

10

20

-А1+В$1+2

2

зо

 

 

Чему станет равно значение ячейки С2, если в нее скопировать формулу из ячейки С1?

Ответ:

9.15. При работе с электронной таблицей в ячейку СЗ записана формула: =$ВЗ+С$2. Какой вид приобретет формула, после того как ячейку СЗ скопируют в ячейку D2?

Ответ:

9.16. При работе с электронной таблицей в ячейку Е5 записана формула: =$СЗ—В$З. Какой вид приобретет формула, после того как ячейку Е5 скопируют в ячейку D3?

Ответ:

9.17. При работе с электронной таблицей в ячейку В4 записана формула: =$А$4+СЗ. Какой вид приобретет формула, после того как ячейку В4 скопируют в ячейку С2?

Ответ:

9.18. В ячейке В1 записана формула: =2 * $А1. Какой вид приобретет формула, после того как ячейку В1 скопируют в ячейку С2?

Ответ:

Напоминание. для наглядного представления табличной информации часто используют диаграммы. В зависимости от необходимого визуального эффекта выбирают тип диаграммы. В основном это Линейчатая и Гистогражжа (горизонтальные или вертикальные прямоугольники), Кольцевая и Круговая, а таюке График и Точечная.

Основное, что вы должны уметь делать, — понимать, что диаграммы строятся на основе данных, находящихся в таблице и что Кольцевая и Круговая диаграммы отображают соотношение этих данных к их общей сумме. А в остальных диаграммах отображаются абсолютные значения.

Примеры .

9.19. Дан фрагмент электронной таблицы:

 

 

в

1

=В1+1

1

2

2

З

=В2-1

 

4

 

 

После выполнения вычислений была построена диаграмма по значениям диапазона ячеек А1 :А4. Укаэките получившуюся диаграмму.

9.20. Дан фрагмент электронной таблицы:

 

 

в

с

 

1

з

 

5

 

2

 

=С1-2

 

В2+С2 6

После выполнения вычислений была построена диаграмма по значениям диапазона

9.21. Дан фрагмент электронной таблицы:

 

 

в

с

 

1

з

 

5

 

2

 

 

 

=C1-1

=А2/2

-В2-С2

После выполнения вычислений была построена диаграмма по значениям диапазона

9.22. В цехе трудятся рабочие трех специальностей — токари (Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд не меньше второго и не больше пятого. На диаграмме отражено количество рабочих с различными разрядами, а на диаграмме II — распределение рабочих по специальностям.

Каждый рабочий имеет только одну специальность и один разряд.

Имеются четыре утверждения:

А) все рабочие третьего разряда могут быть токарями;

Б) все рабочие третьего разряда могут быть фрезеровщиками; В) все слесари могут быть пятого разряда;

Г) все токари могут быть четвертого разряда.

Какое из этих утверждений следует из анализа обеих диаграмм?

Рекомендации. По гистограмме (1 диаграмма) посчитайте, сколько всего рабочих в цехе (второго разряда — 25, третьего — 40, четвертого — 20, пятого — 15; всего 25 + 40 + 20 + 15 = 100). Пользуясь соотношением, полученным из круговой диаграммы (ll диаграмма), вычислите количество токарей, слесарей и фрезеровщиков (токарей половина, то есть 100 12 = 50; фрезеровщиков и слесарей по четверти, то есть по 100 / 4 = 25). Проверьте получившиеся соотношения:

А) рабочих 3-го разряда 40, а токарей — 50. Могут ли быть все 40 рабочих 3-го разряда среди 50 токарей? Да, могут;

Б) рабочих 3-го разряда 40, а фрезеровщиков — 25. Могут ли быть все 40 рабочих 3-го разряда 25 фрезеровщиками? Нет, не могут;

В) слесарей всего 25, а рабочих 5-го разряда — 15. Могут ли быть все 25 слесарей 15 рабочими 5-го разряда? Нет, не могут;

Г) токарей всего 50, а рабочих 4-го разряда — 20. Могут ли быть все 50 токарей 20 рабочими 4-го разряда? Нет, не могут.

9.23. В цехе трудятся рабочие трех специальностей — токари (Т), слесари (С) и фрезеровщики (Ф). Каждый рабочий имеет разряд не меньше второго и не больше пятого. На диаграмме I отражено количество рабочих с различными разрядами, а на диаграмме II — распределение рабочих по специальностям.

Каждый рабочий имеет только одну специальность и один разряд. 1) П)

Имеются четыре утверждения:

а) все рабочие второго разряда могут быть слесарями;

б) все фрезеровщики могут быть четвертого разряда;

в) среди рабочих третьего разряда может не быть ни одного токаря;

г) у всех токарей разряд может быть не меньше четвертого.

Какие из этих утверждений следуют из анализа обеих диаграмм? Обведите буквы, соответствующие этим утверждениям.

9.24. На диаграмме показано количество призеров олимпиады по информатике (И), математике (М), физике (Ф) =Н, fibliтрех городах России.

                                                                                      Екатеринбург             Томск              Н овоси би рек

Какая из диаграмм правильно отражает соотношение общего числа призеров по каждому предмету для всех городов вместе?

                                                             2)          и

м м

м ф

Пример решения

По первой диаграмме получим общее количество призеров по каждому предмету. В Екатеринбурге призеров по математике 180, в Томске — 160, в Новосибирске — 180. Итого призеров по математике 180 + 180 + 160 = 520.

Аналогично получим, что призеров по физике всего 120 + 140 + 120 = 380, а призеров по информатике — 120 + 60 + 120 = 300.

Сложим полученные три суммы и получим, что общее число призеров по всем трем предметам равно 520 + 380 + ЗОО = 1200.

Найдем отношение чйсла призеров по каждому предмету к общему числу призеров.

По математике — 520/1200 — чуть меньше половины.

По физике — 380/1200 — примерно треть.

По информатике — 300/1200 — ровно четверть.

На приведенных диаграммах только первая отображает такое соотношение призеров.

Рекомендация. По первой диаграмме получите общее количество призеров по каждому предмету (сложите). Сложите получившиеся числа и посмотрите, как общее число призеров по каждому предмету соотносится с их общим количеством. Прикиньте, как каждое из получившихся отношений соотносится с половиной и с четвертью. Найдите получившееся соотношение среди приведенных диаграмм,

9.25. В спортивный пионерский лагерь приехали дети из четырех городов, занимающихся тремя видами спорта: футбол, волейбол и баскетбол. На диаграмме показано, сколько детей приехало из какого города. На диаграмме II показано распределение детей по видам спорта.

1)

50

45

40 35

зо 25

20

15

10

5

Имеются четыре утверждения:

а) все футболисты могут быть из Воронежа;

б) среди детей из Тулы может не быть ни одного футболиста;

в) среди волейболистов может не быть ни одного ребенка из Липецка;

г) среди детей из Тулы больше футболистов, чем баскетболистов.

Какие из этих утверждений следуют из анализа обеих диаграмм? Обведите буквы, соответствующие этим утверждениям.

9.26. Дан фрагмент электронной таблицы.

 

 

в

с

D

1

6

 

 

 

2

=D2-B1

-В1/2

=А1-В2

=А1+В1/2

Какое число долэкно быть записано в ячейке В1, чтобы построенная после выполнения вычислениЙ диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку?

РеколденДация. Обозначим искомое число (значение ячейки В1) как Х. Перепишем формулы в ячейках A2:D2. Ячейку А2 посчитаем позже (так как она ссылается на D2). В2 = Х/2, С2 = 6 — Х/2, D2 = 6 + W2, А2 = б + W2 — Х = б — Х/2. Из диаграммы видно, что значение в одной из ячеек в З раза больше остальных (которые совпадают). Среди полученных 4-х формул видно, что D2 больше, чем В2. Значит, именно она — большая. Значит, можно найти Х либо приравняв, например, В2 и С2, либо решив уравнение D2 = З*В2. Приравняем В2 и С2. = 6—W2. Отсюда Х = 6.

 

 

в

с

 

1

 

 

8

 

2

=В1/2

=С1-А2

=D2-A2 -В2

 

        9.27. Дан фрагмент электронной таблицы.                                                         

Какое число должно быть записано в ячейке В1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку?

9.28. При работе с электронной таблицей в ячейку В2 записана формула, вычисляющая произведение числа, находящегося в ячейке А2, на число, находящееся в соседней сверху ячейке (в данном случае В1). Затем эту формулу скопировали в ячейки C2:F2. Укажите формулу, записАнную в ячейке В2.

 

 

в

с

 

 

 

1

 

4

6

8

10

12

2

10

40

60

 

100

120

                       3) -$А$2*В$1                   

Рекомендация. Формула из В2 будет копироваться вправо. При этом будут индексироваться номера столбцов (буквы). Нужно, чтобы номер столбца А не изменился, а номер столбца менялся, соответственно, на C,D,E,F . Значит, знак абсолютной адресации ($) должен стоять перед А и не должен стоять перед В. Что стоит перед номерами строк (числами) не имеет значения, потому что копирования формулы по вертикали не происходит.

9.29. При работе с электронной таблицей в ячейку А2 записана формула, вычисляющая  сумму числа, находящегося в ячейке А1, и удвоенного значения числа, находящегося в соседней справа ячейке (в данном случае В2). Затем эту формулу скопировали в

ячейки АЗ:А5. Укажите формулу, записанную в ячейке А2.

 

 

 

в

1

100

 

2

114

7

з

126

13

4

180

40

5

202

51

                         1)2)             3)                   4)

9.30. При работе с электронной таблицей решили составить таблицу произведений четных и нечетных цифр. Для этого в ячейку В2 записали формулу, которую затем скопировали в остальные ячейки диапазона В2:Е6. Укажите формулу, записанную в ячейке В2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

12

18

 

 

 

10

20

30

40

 

 

14

28

42

56

 

 

18

36

54

72

                                           2) -$А2*$В1                          3)4)

10. БАЗЫ ДАННЫХ

Основные понятия

Одной из самых удобных информационных моделей является база данных.

База Данных информационная модель, хранящая данные о группе объектов с одинаковым набором свойств. Как правило, база данных хранит информацию о нескольких группах объектов, связанных между собой.

В школьном курсе информатики изучают только редячионные базы Данных. В них информация хранится в виде таблиц, связанных между собой отношениями подчинения.

Каждая строка таблицы описывает один объект. Этот объект может иметь различные свойства, информация о которых хранится в столбцах таблицы.

Данные в строках, таким образом, могут быть разных типов. Одна строка- называется записью. Данные в каждом столбце описывают одно свойство объектов. Таким образом, данные в одном столбце имеют одинаковый тип. Столбец таблицы называется полем.

Для указания на конкретный объект (запись) таблицы принято вводить специальный, уникальный набор полей (или одно поле). Такой набор называется ключом, а поле — ключевыж. Самый надежный и удобный способ — в каждой таблице хранить поле с уникальным кодом строки (записи).

Для связи между таблицами в подчиненной таблице используются специальные поля, в которых хранится информация о связанных записях главной таблицы. Обычно — ключ.

Для выбора из базы данных объектов с определенными свойствами используются операции сравнения, а также арифметические и логические операции.

Так как в школьном курсе информатики изучаются только реляционные базы данных, все сказанное ниже относится именно к реляционным базам данных.

Практическая часть

10.1. Укажите одно или несколько правильных утверждений. Буквы, соответствующие правильным утверждениям, обведите, остальные — зачеркните.

Для баз данных справедливо:

а) информация хранится в виде таблиц, связанных отношениями подчинения;

 б) строки таблицы хранят информацию об объектах и называются записями;

                  в) столбцы таблицы хранят информацию о свойствах объектов;      

г) информация в столбце всегда одного типа данных;

д) столбец таблицы называется полем.

Напоминание. Шля осуществления каких-либо действий над записями баз данных необходимо указывать, над какими именно записями нужно осуществить эти действия. для отбора нужных записей используют условия. В условиях указываются имена полей, которые сравниваются друг с другом или с константами при помощи операций соотношения. Эти операции те же, что и в элек тронных таблицах.

10.2. Сопоставьте каждому сравнению (слева) условие, которое это сравнение проверяет (справа). Впишите рядом с буквой сравнения число, соответствующее смыслу этого сравнения:

1) если первый аргумент меньше или равен второму

б)2) если первый аргумент меньше второго

З) если первый аргумент больше или равен второму

4)     если первый аргумент больше второго

5)     если аргументы не равны

6)     если аргументы равны

10.3. В таблице представлены результаты тестирования:

Фамилия

Математика

Физика

Иванов

76

54

Петров

38

74

Сидоров

40

 

Орлов

67

67

Пастухов

38

95

Николаев

23

37

Сколько записей в вышеприведенной таблице удовлетворяют условию

 «Математика > 38»?

Ответ:

10.4. Сколько записей в вышеприведенной таблице удовлетворяют условию

                  «Физика       54»?

Ответ:

10.5. Сколько записей в вышеприведенной таблице удовлетворяют условию

«Физика >= Математика»?

Ответ:

10.6. Сколько записей в вышеприведенной таблице удовлетворяют условию

«Физика <> Математика»?

Ответ:

10.7. Сколько записей в вышеприведенной таблице удовлетворяют условию

«Математика <> 38»?

Ответ:

Напоминание. Если требуется проверить сразу несколько условий, возникает необходимость объединить эти условия. для этого, как вы помните из алгебры логики, используются логические операции.

10.8. Сопоставьте каждой логической операции (слева) ее смысл (справа). Впишите рядом с буквой операции число, соответствующее смыслу этой операции:

1) результат меняется на противоположный.

Если операнд — ИСТИНА, результат — ЛОЖЬ. И наоборот 6) или 2) результат — ИСТИНА, если оба операнда — ИСТИНА

           в) НЕ                       З) результат — ИСТИНА, если хотя бы один операнд — ИСТИНА

Напоминание. Если в выражении присутствует несколько логических операций, они выполняются в соответствии со своими приоритетами.

10.9. Укажите порядок выполнения операций в соответствии с их приоритетом (от высшего к низшему). В ответе укажите буквы, соответствующие операциям, в указанном порядке.

                  а) ИЛИ                       б) выражение в скобках                          в) и                             г) НЕ

Ответ:

10.10. Результаты тестирования представлены в таблице:

 

Фамилия

Пол

Математика

Русский язык

Химия

Информатика

Биология

Аганян

 

82

56

 

32

70

Воронин

м

 

62

45

74

23

Григорчук

м

54

74

68

75

83

Роднина

 

71

63

56

82

79

Сергеенко

 

33

25

74

38

 

Черепанова

 

18

92

83

28

61

Сколько записей в ней удовлетворяют условию «Пол='ж' ИЛИ Химия>Биология»?

Рекомендация. Выберите записи, которые удовлетворяют первому условию (Пол='ж'). Отметьте их (например, «галочками»). Затем выберите записи, удовлетворяющие второму условию (Химия>Биология). Тоже отметьте их «галочками». Так как для их объединения используется логическая операция ИЛИ, ей удовлетворяют те записи (строки), в КОТОРЫХ мы поставили хотя бы одну

«галочку».

10.11. Результаты тестирования представлены в таблице:

 

Фамилия

Пол

Математика

Русский язык

Химия

Информатика

Биология

Аганян

 

82

56

 

32

70

Воронин

м

 

62

45

74

23

Григорчук

м

54

74

68

75

83

Роднина

 

71

63

56

82

79

Сергеенко

 

33

25

74

38

46

Черепанова

 

18

92

83

28

61

Сколько записей в ней удовлетворяют условию «НЕ(Пол='ж' И Математика<Биология)»?

Рекомендация. Такие задания (с операцией НЕ перед всем выражением) можно решать двумя способами. Либо выберите записи, которые удовлетворяют выражению. Тогда все остальные бу- дут ему НЕ удоблетворять, то есть именно то, что нужно найти.

Либо примените закон де Моргана. Но в этом случае нужно быть очень осторожным и не забыть обратить все условия. В данном случае:

НЕ(Пол='ж' И Математика<Биология) =

НЕ(Пол='ж') ИЛИ НЕ(Математика<Биология) =

Пол<>'ж' ИЛИ Математика>=Биология

10.12, Результаты тестирования представлены в таблице:

Фамилия

Пол

Математика

Русский язык

Химия

Информатика

Биология

Аганян

 

82

ч56

46

32

70

Воронин

м

43

62

45

74

23

Григорчук

м

54

74

68

75

83

Роднина

 

71

63

56

82

79

Сергеенко

 

33

25

74

38

46

Черепанова

 

18

92

83

28

61

Сколько записей в ней удовлетворяют условию «Пол='ж' И Математика>Химия»?

       10.13. Результаты тестирования представлены в таблице:           

Фамилия

Пол

Математика

Русский язык

Химия

Информатика

Биология

Аганян

 

82

56

46

32

70

Воронин

м

43

62

45

74

23

Григорчук

м

54

74

68

75

83

Роднина

 

71

63

56

82

79

Сергеенко

 

33

25

74

38

46

Черепанова

 

18

92

83

28

61

Сколько записей в ней удовлетворяют условию

«Пол='ж' И Математика>Русский язык ИЛИ Пол='м' И Информатика>Биология»?

1) 15

Рекомендация. Не забудьте, что приоритет операции «Логическое И» выше, чем у операции «Логическое ИЛИ».

10.14. Из правил соревнования по тяжелой атлетике:

« Тяжелая атлетика это прямое соревнование, когда каждый атлет имеет три попытки в рывке и три попытки в толчке. Самый тяжелый вес поднятой штакги в каж- дом упражнении суммируется в общем зачете. Если спортсмен потерпел неудачу во всех трех попытках в рывке, он может продолжить соревнование в толчке, но уже не сможет занять какое-либо место по сумме двух упражнений.

Если два спортсмена заканчивают состязание с одинаковым итоговым результатом, высшее место присуждается спортсмену с меньшим весом. Если же вес спортсменов одинаков, преимущество отдается тому, кто первым поднял победный вес».

Таблица результатов соревнований по тяжелой атлетике:

Фамилия, И.О.

Вес спортсмена

Взято в рывке

Рывок с попытки

Взято в толчке

Толчок с попытки

Айвазян Г.С.

77,1

150,0

з

200,0

2

Викторов М.П.

79,1

147,5

1

202,5

1

Гордезиани Б.Ш.

78,2

147,5

2

200,0

1

Михальчук М.С.

78,2

147,5

2

202,5

з

Пай С.В.

79,5

150,0

1

200,0

1

Шапсугов М.Х.

77,1

147,5

1

200,0

1

Кто победил в общем зачете (сумме двух упражнений)?

1) Айвазян Г.С. З) Михальчук М.С. 2) Викторов М.П. 4) Пай С.В.

10.15. В таблице собраны сведения о членах школьной волейбольной команды:

 

Фамилия

Вес

Рост

Пол

ванов

87

180

м

Петрова

55

170

ж

идоров

67

155

м

упкина

78

160

ж

Сколько записей удовлетворяют условию:

девочки выше 165 см И легче 60 кг ИЛИ учащиеся тяжелее 75 кг?

Ответ:

10.16. На городской олимпиаде по программированию предлагались задачи трех типов: А, В и С. По итогам олимпиады была составлена таблица, в колонках которой указано, сколько задач каждого типа решил участник. Вот начало таблицы:

Фамилия

 

в

 

Иванов

з

2

1

За правильное решение задачи типа А участнику начислялся 1 балл, за решение задачи типа В — 2 балла и за решение задачи типа С — З балла. Победитель определялся по сумме баллов, которая у всех участников оказалась разная. Какой запрос достаточно выполнить для определения победителя олимпиады из следующих:

1)    отсортировать таблицу по возрастанию значения поля С и взять первую строку

2)    отсортировать таблицу по убыванию значения поля С и взять первую строку

З) отсортировать таблицу по убыванию значения выражения А + 2В + ЗС и взять первую строку

4) отсортировать таблицу по возрастанию значения выражения А + 2В + ЗС и взять первую строку

Рекомендация. Проанализируйте принцип начисления баллов и выведите формулу суммы баллов. Если победитель выбирается из первой строки запроса, проанализируйте, какое количество баллов он должен набрать — наибольшее или наименьшее? Как в этом случае должна быть отсортирована таблица?

10.17. На городской олимпиаде по программированию предлагались задачи трех типов: А, В и С. По итогам олимпиады была составлена таблица, в колонках которой указано, сколько задач каждого типа решил участник. Вот начало таблицы:

Фамилия

 

в

 

Иванов

4

1

з

За правильное решение задачи типа А участнику начислялся З балла, за решение задачи типа В — 2 балла и за решение задачи типа С — 1 балл. Победитель определялся по сумме баллов, которая у всех участников оказалась разная. Какой запрос достаточно выполнить для определения победителя олимпиады из следующих:

1)    отсортировать таблицу по возрастанию значения поля С и взять первую строку

2)    отсортировать таблицу по убыванию значения поля С и взять первую строку

З) отсортировать таблицу по возрастанию значения выражения ЗА + 2В + С и взять первую строку

4) отсортировать таблицу по убыванию значения выражения ЗА + 2В + С и взять первую строку

10.18. Ниже приведены фрагменты таблиц базы данных канцелярского магазина:

Вид изделия

Код изделия

 

Авторучка

001

 

Фломастер

002

 

Карандаш

003

 

 

Цвет изделия

Код цвета

 

 

синий

01

 

 

зеленый

02

 

 

красный

оз

 

Размер изделия

Код размера

 

большой

0001

 

маленький

0002

 

 

Артикул

Изделие

Размер

Цвет

Цена

8457

002

0002

01

5

2537

003

0001

01

9

4758

002

0002

02

5

5748

003

0001

02

8

3647

001

0001

02

9

1948

003

0002

01

6

3937

001

0001

01

8

3524

002

0001

оз

8

1362

002

0002

оз

6

Сколько стоит набор, состоящий из 10 больших синих карандашей и 20 маленьких красных фломастеров?

Рекомендация. Основной принцип базы данных— связанные друг с другом таблицы. Обычно связь осуществляется по некоторому полю — коду записи одной из таблиц. В данном случае главная таблица (последняя) ссылается на три предыдущих таблицы. Так как нас просят найти комбинацию двух видов предметов, будем искать их отдельно друг от друга. По первым трем таблицам определим, что большой синий карандаш — это 0001 (большой), 01 (синий), 003 (карандаш). В последней таблице найдем строку с такими кодами. Это вторая строка (артикул 2537). Цена одного карандаша равна 9. Значит, 10 карандашей будут стоить 90. Аналогично найдем маленький (0002) красный (03) фломастер (002). Это последняя строка. цена одного такого фломастера равна 6. Значит, 20 фломастеров будут стоить 120. Теперь сложим получившиеся числа и найдем ответ.

10.19. Ниже приведены фрагменты таблиц базы данных канцелярского магазина:

 

Вид изделия

Код изделия

 

 

Авторучка

001

 

 

Фломастер

002

 

 

Карандаш

003

 

 

Цвет изделия

Код цвета

синий

01

зеленый

02

красный

оз

 

 

Размер изделия

Код размера

 

 

большой

0001

 

 

маленький

0002

 

 

Изделие

Размер

цена

 

 

001

0001

 

 

 

002

0001

 

 

 

003

0001

10

 

 

001

0002

 

 

 

002

0002

 

 

 

003

0002

 

 

 

Артикул

Изделие

Размер

Цвет

Количество

 

1362

002

0002

оз

10

 

1948

003

0002

01

15

 

2537

003

0001

01

20

 

3524

002

0001

оз

15

 

3647

001

0001

02

25

 

3937

001

0001

01

20

 

4758

002

0002

02

10

 

5748

003

0001

02

5

 

8457

002

0002

01

15

Один из покупателей попросил продать ему все красные изделия, которые есть в магазине. Сколько он должен за них заплатить?

10.20. Ниже приведены две таблицы из базы данных. Каждая строка таблицы 2 содержит информацию о ребенке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. Определите на основании приведенных данных фамилию и инициалы внука Дени К. Д.:

                                     Таблица 1                                                             Таблица 2

ID

Фамилия И.О.

пол

 

ID Ребенка

42

Бабенко А.Е.

м

53

42

82

Сорт А.К.

ж

21

42

53

Марченко Е.Е.

м

71

53

21

ирта О.Б.

ж

14

53

26

Гано И.Е.

ж

 

14

71

Камо Е.А.

м

78

14

14

дени К.Д.

ж

71

26

34

Ивенко Д.Я.

м

14

26

78

Исава Г.А.

ж

26

82

57

Арне А.А.

м

57

78

                      1) Бабенко А.Е.             2) сорт А.К.               3) ирта О.Б.                4) Арне А.А.

Решение. Анализируя задачу, замечаем, что таблица 2 хранит информацию о родственных связях, а таблица 1 — отношение lD человека с его фамилией и полом. .для начала найдем lD требуемого Дени К.Д. Из первой таблицы понимаем, что это 14. Далее нас интересует его внук. Это значит, что нас интересуют дети его детей. По второй таблице найдем всех детей родителя 14. Это 53 и 26. Теперь найдем всех детей родителей 53 и 26. Это 42 и 82. Но нас интересует внук

Дени К.Д. То есть этот человек должен быть мужского пола. По таблице 1 находим пол человека 42 (М) и 82 (Ж). Значит, нужный нам человек имеет lD=42. Это Бабенко А.Е. В списке вариантов он под номером 1.

10.21. Ниже приведены две таблицы из базы данных. Каждая строка таблицы 2 содержит информацию о ребенке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. Определите на основании приведенных данных фамилию и инициалы деда Глянко Е.Е.:

                                  Таблица 1                                                       Таблица 2

 

 

Фамилия И.О.

Пол

 

ID Ребенка

14

Шичко К. Д.

ж

71

26

17

Карно Г.Е.

м

63

17

21

Басик О.Б.

 

14

53

26

Гилава И.Е.

ж

 

14

34

Красик Д.О.

м

14

26

48

Арис И.Г.

м

17

48

53

Глянко Е.Е.

м

71

53

57

Орба

м

57

78

71

Варус Е.А.

м

78

14

78

Гудько Г.Е.

ж

26

82

82

Асава С.К.

ж

21

17

                     1) Гудько Г,Е.                 2) Арис И.Г.              3) Красик Д.О.             4) Карно Г.Е.

10.22. Те же таблицы, что в задаче 10.21. Определите на основании приведенных данных фамилию и инициалы племянницы Глянко Е.Е. (племянница — дочь брата или сестры):

                     1) Шичко К.Д.                2) Асава С.К.            3) Васик О.Б.                 4) Гилава И.Е.

10.23. Те же таблицы, что в задаче 10.21. Определите на основании приведенных данных фамилию и инициалы тети Карно Г.Е. (тетя — сестра отца или матери):

                     1) Басик О.Б.                       2) Шичко К.Д. З) Асава С.К.                    4) Гилава И.Е.

11. СЕТЕВЫЕ ТЕХНОЛОГИИ

основные понятия

Адресация в Интернете. Для обмена информации между компьютерами необходимы:

• канал связи, по которому идет передача данных;  аппаратные средства, которыми компьютер связывается с каналом связи (модем, сетевая карта);  программные средства, которыми при этом пользуется компьютер или человек (браузер, почтовая программа, менеджер обмена сообщениями);  протокол (соглашение, согласно которому происходит процедура обмена).

 Для соединения через Интернет каждый компьютер должен обладать протоколом TCP/IP. Согласно этому протоколу, в частности, каэкдый компьютер должен иметь уникальный адрес, состоящий из четырех чисел (от О до 255 каэкдое), разделенных точками (например, 172.16.1.95). Это называется 1Р-аДрес. Так как каждое число 1Р-адреса лежит в диапазоне 0—255, нетрудно подсчитать, что для его хранения требуется 8 бит, то есть 1 байт.

Также нетрудно подсчитать, что общее количество 1Р-адресов не может быть больше чем 2564 . То есть около 4 миллиардов. Это, однако, не означает, что к Интернету не может быть подключено больше 4 миллиардов компьютеров. Специальные технологии позволяют целой группе компьютеров использовать один общий 1Р-адрес для выхода в Интернет.

Некоторые компьютеры в сети предоставляют свои ресурсы в общее пользование. Они называются серверами. Как правило, это серверы с информацией. Так как множество людей часто обращаются к серверам, неудобно помнить для каждого нужного сервера его 1Р-адрес. Для таких серверов используются буквенные названия, которые называются Доменным адресож. Например, www.mail.ru. Когда нужно обратиться к серверу по доменному адресу, компьютер сначала посылает запрос в специальную службу (она называется DNS), которая по доменному адресу выдает 1Р-адрес этого сервера.

Доменные адреса обычно выбирают по территориальному принципу или по принципу принадлежности сервера к организации какого-либо типа.

Пример территориального принципа выбора доменного адреса: sch239.spb.ru (Россия, Санкт-Петербург, школа 239).

По принципу принадлежности организации к какому-либо типу обычно действуют организации из США (родины Интернета). Примеры: whitehouse.gov, pentagon.mil, greenpeace.org, mti.edu.

Для указания местоположения какого-либо ресурса (файла) в сети Интернет используют URL (универсальный указатель местоположения ресурса). Он состоит из трех частей: имени протокола, по которому будет происходить передача файла, затем через символы «://» адрес компьютера, на котором этот файл хранится (1Р-адрес или доменный адрес), затем через символ «/» имя файла на этом компьютере (иногда с указанием пути к файлу). Пример: http://masha.ru/risunok.jpg.

Для поиска информации в Интернете используют поисковые системы специальные программно-аппаратные комплексы (базы данных), которые хранят информацию о множестве страниц Интернета и которые предоставляют возможность поиска среди этой информации.

Для поиска нужно указать ключевые слова, которые должны содержаться в искомом документе. Чтобы указать, должны ли эти слова присутствовать в документе одновременно или же достаточно одного из них, используют логические операции (И и ИЛИ). Операцию И обозначают значком «&» (амперсанд), операцию ИЛИ обозначают значком «l» (вертикальная черта). Приоритет операции И выше, чем у операции ИЛИ.

Для изменения порядка выполнения операций используют скобки.

Если несколько ключевых слов объединены операцией И, количество найденных страниц будет меньше, чем если эти слова искать по отдельности.

Если несколько ключевых слов объединены операцией ИЛИ, количество найденных страниц будет, наоборот, больше.

Практическая часть

11.1. Укажите одно или несколько правильных утверждений. Буквы, соответствующие правильным утверждениям, обведите, остальные — зачеркните.

Для компьютерной сети Интернет справедливо:

а) каждый компьютер, подключенный к сети, должен иметь собственный адрес — 1Р-адрес

б) 1Р-адрес состоит из четырех чисел, разделенных точками

в) для хранения каждого из чисел 1Р-адреса выделяют по 1 байту

г) каждое из чисел 1Р-адреса может быть от О до 255

д) некоторые числа 1Р-адреса можно заменять на слова (например, www.mail.ru)

е) некоторые комбинации чисел 1Р-адреса неприемлемы ввиду договоренностей об 1Р-адресах

ж) наибольшее значение (255) для чисел в 1Р-адресе происходит от размера ячейки памяти, выделяемой для 1Р-адреса

з) общее количество 1Р-адресов, которое может существовать, составляет 2564 (примерно 4 миллиарда)

и) количество компьютеров в сети не может превышать четырех миллиардов ввиду ограничения на количество возможных 1Р-адресов

11.2. Сколько точек в 1Р-адресе?

Ответ:

11.3. Петя записал 1Р-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами 1Р-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите 1Р-адрес.

В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем 1Р-адресу.

                                                                           в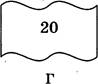               

Ответ:

Рекомендация. Честно говоря, мы заметили, что проще всего решать такую задачу, действительно написав на четырех клочках бумаги куски 1Р-адреса и перекладывая их. Правда, мы не уверены, что если вы начнете заниматься этим на экзамене, вам не сделают замечание.

Основная идея решения этой задачи— в недопустимости чисел 1Р-адреса, которые превышают 255. В данном случае задача решается совсем просто, ввиду быстрого установления двух обрывков на свои места. Обрывок А не может быть первым (из-за точки). Кроме того, так как число в нем больше 25, то справа к нему нельзя дописать ни одйой цифры, иначе получатся числа больше 640. Значит, 64 — одно из чисел 1Р-адреса, причем не первое. А так как больше обрывков, начинающихся с точки, нет, значит, обрывок А стоит последним.

К обрывку В не может быть приставлена справа ни одна цифра, так как число 133 уже трехзначное. Значит, обрывок В должен быть или последним, или после него должна стоять точка. Последнее место уже занято. Значит, обрывок В предпоследний. Оставшиеся 2 варианта нетрудно просто проверить.

11„4. Петя записал 1Р-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами 1Р-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите 1Р-адрес.

В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем ЕЈ¯ЕЈ1Р-адресу.

в

Ответ:

11.5. Петя записал 1Р-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами 1Р-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите 1Р-адрес.

В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем ггј-т1Р-адресу.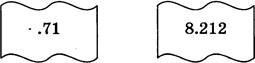

в

Ответ:

11.6. Укажите одно или несколько правильных утверждений. Буквы, соответствующие правильным утверждениям, обведите, остальные — зачеркните.

а) Для указания местоположения ресурса в сети Интернет используется специальный адрес, называемый URL

                   б) URL — Uniform Resource Iocator

в) URL состоит из трех частей — протокол, символы «://», адрес компьютера в сети, символ «/» , местоположение файла на этом компьютере

г) Пример URL: «http://www.prazdnik.ru/files/holyday.jpg»

д) Протокол — договоренность о способе обмена информацией

е) Примеры наиболее часто используемых протоколов: http, ftp

ж) Адрес компьютера в URL может быть доменным или

з) Допустимым считается, например, такой URL: «ftp://10.20.4.58/index.html»

и) Местоположение файла в URL может включать в себя последовательность имен папок от «стартового положения» файлов на сервере, разделенных символами «/»

к) URL всегда заканчивается именем файла

11.7. Доступ к файлу htm.net, находящемуся на сервере com.edu, осуществляется по протоколу ftp. В таблице фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла в сети Интернет.

 

 

 

Б

сот

в

.edu

 

 

 

.net

Е

htm

Ж

ftp

Ответ:

Рекомендация. Чтобы не ошибиться в символах и буквах, сначала аккуратно запишите на черновике получающийся URL. Не забудьте записать между протоколом и именем сервера символы «:ll», а между именем сервера и именем файла — символ «1». Не старайтесь использовать привычные имена серверов и имена файлов. Не старайтесь расставлять их в том порядке, как вы привыкли ими пользоваться. Просто «тупо» запишите последовательность, которая указана в задаче: протокол, «:ll», имя сервера, «1», имя файла. Потом подпишите под каждой из получившихся частей URL свою букву по таблице. Не забудьте проверить, что у вас получились все 7 букв и что они не повторяются.

11.8. Доступ к файлу www.txt, находящемуся на сервере http.net, осуществляется по протоколу ftp. В таблице фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла.

А

http

Б

.txt

в

.net

 

 

д

 

Е

WWW

 

 

Ответ:

11.9. Доступ к файлу txt.com, находящемуся на сервере www.ftp, осуществляется по протоколу http. В таблице фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла.

 

.ftp

 

txt

в

 

 

 

 

htt

 

 

ж

. сот

Ответ:


11.10. Доступ к файлу com.ftp, находящемуся на сервере www.edu, осуществляется по протоколу http. В таблице фрагменты адреса файла закодированы буквами от А до Ж. Запишите последовательность этих букв, кодирующую адрес указанного файла.

 

.ft

 

 

в

.edu

 

 

 

 

 

сот

ж

http

Ответ:

Напоминание. Поиск информации в Интернете.

При пользовании поисковыми системами запрос, который делает пользователь, обрабатывается базой данных, хранящейся на поисковом сервере. Ключевые слова, которые вводит пользователь в тексте запроса, ищутся по отдельности в базе данных, после чего результаты каждого поиска соединяются в зависимости от логических операций, которыми объединены ключевые слова. Если используется логическая операция «И», то в результат войдут только те страницы, которые содержат одновременно оба ключевых слова (мы говорим «оба», так как логические операции «И» и «ИЛИ» всегда имеют ровно два операнда). Значит, в результате поиска количество страниц, которое найдет поисковый сервер, будет меньше, чем в запросах по каждому ключевому слову в отдельности.

Если используется логическая операция «ИЛИ», то в результат войдут как страницы, которые содержат только одно из ЮПЮЧеВЫХ слов, так и страницы, которые содержат только второе ключевое слово. Таюке результат будет содержать страницы, которые содержат сразу оба КГ1ЮЧеВЫХ слова. Значит, в результате поиска количество страниц, которое найдет поисковый сервер, будет больше, чем по каждому ключевому слову в отдельности.

Не забудьте, что приоритеты логических операций здесь действуют как обычно. Приоритет операции «И» выше, чем у операции «ИЛИ» (см. главу 4 «Основы логики»).

Замечание. Мы, конечно, слегка грешим против истины, для упрощения понимания. В действительности правильнее говорить, что результат запроса с логической операцией «И» не больше результата запроса с каждым юпючевым словом в отдельности. Так же как и результат запроса с логической операцией «ИЛИ» не меньше запросов с этими словами по отдельности.

Эта оговорка работает, когда, например, в базе данных существуют только страницы, в которых оба КЛЮЧеВЫХ слова встречаются одновременно, а по отдельности эти ключевые слова не встречаются. Но мы такой случай для общности и простоты задачи, не рассматриваем. Вам мы советуем при решении такого типа задач тоже считать, что это не наш случай.

11.11. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции «ИЛИ» в запросе используется символ 1, а для логической операции «И» — &.

 

1

принтеры продажа

2

п инте ы

З

принтеры & продажа

Ответ:

1132. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции «ИЛИ» в запросе используется символ а для логической операции «И» — &.

1

коньки лыжи

2

коньки & лыжи & санки

з

коньки & лыжи

4

лыжи

Ответ:

11.13. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции «ИЛИ» в запросе используется символ 1, а для логической операции «И» — &.

1

принтеры & сканеры & продажа

2

принтеры & продажа

з

принтеры продажа

4

принтеры сканеры продажа

Ответ:

Рекомендация. Учтите, что условие «логическое И» приводит к уменьшению количества найденных страниц. Соответственно, применение нескольких «логических И» еще более уменьшает число найденных страниц.

В отличие от «И», «логическое ИЛИ» приводит к увеличению числа найденных страниц. Соответственно, применение нескольких «логических ИЛИ» еще более увеличивает количество найденных страниц.

 Постарайтесь быть внимательным и обратить внимание на порядок возрастания/убывания. При возрастании нужно сначала указать самое строгое условие (наименьшее число найденных страниц), а в конце — самое «широкое» (больше всего «ИЛИ»). При убывании — наоборот, в обратном порядке.

11.14. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции «ИЛИ» в запросе используется символ , а для л(Яической операции «И» — &.

1

физкультура

2

физкультура & подтягивания & отжимания

з

физкультура & подтягивания

4

физкультура фитнесс

Ответ:

11.15. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции «ИЛИ» в запросе используется символ а для логической операции «И» — &.

1

алгоритм & (программа данные)

2

алгоритм & программа & данные

з

программа данные

4

алгоритм I программа данные

Ответ:

11.16. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции «ИЛИ» в запросе используется символ l, а для логической операции «И» — &.

11.17. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции «ИЛИ» в запросе используется символ 1, а для логической операции «И» — &.

 

1

алгоритм I программа & данные

2

алгоритм I программа данные

з

программа & данные

4

алгоритм & программа & данные

Ответ:

11.18. В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции «ИЛИ» в запросе используется символ 1, а для логической операции «И» —

1

рога & копыта хвосты

2

рога копыта хвосты

з

рога & копыта

4

рога & (копыта хвосты)

Ответ:

Пример. В классе учатся 25 человек. Из них 17 человек ходят на кружок по волейболу  и 13 человек ходят на шахматный кружок. Известно, что ни в один кружок не ходят 6 человек. Сколько человек занимаются и волейболом и шахматами?

Решение:

Эта задача не относится к категории сетевых технологий. Но понимание ее решения потребуется для решения новых заданий на количество запросов к поисковому серверу (которые будут рассмотрены ниже).

Нагляднее всего для решения воспользоваться диаграммой Эйлера:

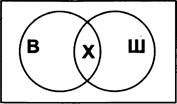
Прямоугольником обозначено все множество учащихся класса. Кругами, помеченными буквами В и Ш обозначены те учащиеся, которые занимаются волейболом и шахматами соответственно. На пересечении кругов находится то множество, размер которого мы должны определить (обозначено буквой Х). Напишем на диаграмме числовые значения, которые нам известны:

 

25

(6)

В скобках написано число учащихся из общего множества, которые не принадлежат множествам В и Ш. Выразим через Х размеры множеств, изображенных на диаграмме. Тогда количество учащихся, которые ходят только на волейбол, будет равно 17 — Х. А количество учащихся, которые ходят только на шахматы, будет равно 13 — Х.

Из диаграммы видно, что число учащихся, которые занимаются хотя бы в одном кружке, с одной стороны, равно 25—6. С другой стороны, равно (17 — Х) + Х + (13 — Х). Приравняем эти два выражения, раскроем скобки и выразим Х. Получим 25 — 6 = (17 —- Х) + Х + (13 — Х) ф 19 - 17 - Х + Х + 13-Х— 19 =  11.

Другой способ решения:

Воспользуемся формулой включений и исключений из комбинаторики:

В приведенной формуле имеется некоторая математическая неточность, связанная с тем, что в ней используются обозначения самих множеств, в то время как предполагается, что действия выполняются над мощностями множеств. Мы решили не добавлять в формулу обозначения мощностей множеств, чтобы не загромождать ее.

В Ш — объединение множеств В и Ш. В нашем случае объем этого множества равно 25 - 6 = 19.

В & Ш — пересечение множеств В и Ш.. В нашем случае это искомая величина. Обозначим ее за Х. Подставляем известные значения, получаем уравнение: 19 17 + 13 — Х, Отсюда находим х = 11.

Заметим, что для трех переменных (Х, У, Z) формула включений и исключений выглядит так: X l Y l Z = X + Y + Z - (Х  Z.

Пример. При попытке осуществить запросы к поисковому серверу было найдено следующее количество страниц по каждому запросу:

Запрос

Количество страниц

г юмзики

1300

изямые

1900

грюмзики & изямые

700

Сколько страниц будет найдено по запросу грюмзики I изямые?

Решение:

По формуле включений и исключений:

грюмзики изямые = грюмзики + изямые — грюмзики & изямые

После подстановки получаем: грюмзики изямые - — 1300 + 1900 700 - 2500.

11.19.

а) При попытке осуществить запросы к поисковому серверу было найдено следующее количество страниц по каждому запросу:

Запрос

Количество страниц (в тысячах)

математика

4300

физика математика

6700

физика & математика

2100

Сколько страниц будет найдено по запросу физика?

Ответ:

б) При попытке осуществить запросы к поисковому серверу было найдено следующее количество страниц по каждому запросу:

Запрос

Количество страниц (в тысячах)

клубника

4600

ежевика

6300

клубника ежевика

8700

Сколько страниц будет найдено по запросу клубника & ежевика?

Ответ:

в) При попытке осуществить запросы к поисковому серверу было найдено следующее количество страниц по каждому запросу:

Запрос

Количество страниц (в тысячах)

тыква

3500

арбуз

2800

тыква & а буз

1400

тыква & дыня

900

арбуз & дыня

1700

тыква & арбуз & дыня

500

тыква арб з дыня

7200

Сколько страниц будет найдено по запросу дыня?

Ответ:

г) При попытке осуществить запросы к поисковому серверу было найдено следующее количество страниц по каждому запросу:

Запрос

Количество страниц (в тысячах)

Диван

3400

чемодан

5200

саквояж

2700

Диван & чемодан

1600

Диван & саквояж

1200

чемодан & саквояж

1300

Диван чемодан саквояж

8300

Сколько страниц будет найдено по запросу Диван & чемодан саквояж?

Ответ:

Пример. По правилам адресации в сетях TCP/IP каждому компьютеру выдается уникальный номер — 1Р-адрес. При этом считается, что каждый компьютер находится в некоторой сети, размер которой задается при помощи так называемой маски сети. Записав в двоичном представлении 1Р-адрес компьютера и маску сети и осуществив между ними поразрядную конъюнкцию, можно получить адрес сети. Определите адрес сети, если известно, что:

1Р-адрес компьютера: 10.0.63.18

Маска сети: 255.255.252.0

Ответ закодируйте при помощи таблицы:

 

в

 

 

 

 

 

н

10

 

15

60

100

56

1

156

При этом точки записывать не нужно.

Решение:

Для получения адреса сети нужно записать в двоичной системе друг под другом 1Р-адрес компьютера и маску сети. При этом нужно учитывать, что каждое из чисел 1Р-адреса и маски сети хранится в 8-разрядном двоичном виде. После этого нужно осуществить поразрядную конъюнкцию этих чисел. После чего записать результат снова в десятичном виде. Так как 255 это 8 подряд идущих единиц в двоичной системе, то в результате поразрядной конъюнкции с любым 8-разрядным числом ответом будет это же число. Поэтому (так как в маске сети первые два числа равны 255) первые два числа искомого адреса будут такими же, как и в 1Р-адресе (10.0). Так как О в 8-разрядном представлении является числом с 8-ю нулями, то поразрядная конъюнкция с ним превращает любое число в ноль. Поэтому последняя часть адреса сети будет ноль (О). Остается вычислить только третью часть адреса. Переведем в двоичную систему числа 63 и 252 и запишем их в 8-разрядном виде друг под другом:

зультате получаем адрес сети: • 10.0.60.0. Найдем в таблице значения 10, О, 60 и О и выпишем соответствующие буквы в этом порядке.

Ответ: ABDB

11.20. По правилам адресации в сетях TCP/IP каждому компьютеру выдается уникальный номер — 1Р-адрес. При этом считается, что каждый компьютер находится в некоторой сети, размер которой задается при помощи так называемой маски сети. Записав в двоичном представлении 1Р-адрес компьютера и маску сети и осуществив между ними поразрядную конъюнкцию, можно получить адрес сети. Определите адрес сети, если известно, что:

ЛР-адрес компьютера: 10.100.65.219

Маска сети: 255.224.0.0

Ответ закодируйте при помощи таблицы:

 

в

с

 

 

 

 

н

10

 

65

119

100

96

192

156

При этом точки записывать не нужно. Отёет:

Пример. В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть 1Р-адреса узла сети относится к адресу сети, а какая к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IPадрес, — в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда — нули.

Адрес сети получается в результате применения поразрядной конъюнкции к заданному 1Р-адресу узла и маске.

Например, если 1Р-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с 1Р-адресом 117.191.88.37 адрес сети равен 117.191.80.0. Чему равен третий слева байт маски? Ответ запишите в виде десятичного числа.

Решение:

В результате поразрядной конъюнкции число 88 превратилось в число 80. Переведем оба числа в двоичную систему счисления и запишем друг под другом.

88 = 10110002, 80 = 10100002.

1011000

1010000

Видим, что первые З цифры (101) остались неизменными, а четвертая цифра (1) превра- тилась в О. Значит, именно в этом месте в маске стоит О. Так как маска состоит из последовательности единиц, за которой стоят нули, то именно в этом месте единицы меняются на нули. Получается, что маска — это 11100002. Однако этот ответ неверный, потому что нас спрашивают третий БАЙТ маски. А в нашей маске только 7 бит. Значит, нужно добавить еще один бит слева. Это должна быть 1, так как в маске сначала стоят единицы. Значит, 240.

11.21. В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть 1Р-адреса узла сети относится к адресу сети, а какая — к адресу са мого узла в этой сети. Обычно маска записывается по тем же правилам, что и IPадрес, — в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда — нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному 1Р-адресу узла и маске.

Например, если 1Р-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с 1Р-адресом 117.191.59.37 адрес сети равен 117.191.48.0. Чему равен третий слева байт маски? Ответ запишите в виде десятичного числа.

11„22. В терминологии сетей TCP/IP маской сети называется двоичное число, определяю щее, какая часть 1Р-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IPадрес, — в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда — нули.

Адрес сети получается в результате применения поразрядной конъюнкции к заданному 1Р-адресу узла и маске.

Например, если 1Р-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с 1Р-адресом 193.212.179.92 адрес сети равен 193.212.160.0. Чему равен третий слева байт маски? Ответ запишите в виде десятичного числа.

11.23. В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть 1Р-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и IPадрес, — в виде четырех байтов, причем каждый байт записывается в виде десятичного числа. При этом в маске сначала (в старших разрядах) стоят единицы, а затем с некоторого разряда — нули. Адрес сети получается в результате применения поразрядной конъюнкции к заданному 1Р-адресу узла и маске.

Например, если 1Р-адрес узла равен 231.32.255.131, а маска равна 255.255.240.0, то адрес сети равен 231.32.240.0.

Для узла с 1Р-адресом 57.137.106.197 адрес сети равен 57.137.64.0. Чему равен третий слева байт маски? Ответ запишите в виде десятичного числа.

Ответы

1.  Количество информации. Скорость передачи информации

1.1.          в), е); 1.2. а), 6), г), д); 1.3. 1; 1.4. З; 1.5. З; 1.6. 7; 1.7. 6; 1.8. 8; 1.9. 250; 1.10. 490;

1.11. 420; 1.12. 600; 1.13. 560; 1.14. 600; 1.15. 10; 1.16. 5; 1.17. 10; 1.18. 2048; 1.19. 128;

1.20. 25; 1.21. 40; 1.22. 32; 1.23. 8; 1.24. 37,5; 1.25. 3750; 1.26. з; 1.27. 96; 1.28. 108; 1.29. 4;

1.30. 320; 1.31. 800; 1.32. 322; 1.33. 260; 1.34. А122; 1.35. А1З; 1.36. БЗ•, 1.37. 405; 1.38. 256;.

1.39. 108; 1.40. 500; 1.41. 1000; 1.42. 600; 1.43. 500; 1.44. 900.

2.  Системы счисления

2.1.          Система счисления — б); алфавит системы счисления — г); мощность алфавита — а); основание системы счисления — д).

2.2.          Для каэкдого числа позиционной системы счисления — вес цифры зависит от ее положения в числе.

2.3.          В основание (в десятичной — в 10, в восьмеричной —

2.4.          N, О, N—1; 2.5. 10N; 2.6. О и 1; 2.7. 6, А, пятнадцать.

2.8.   52436 — разряды, 43210 — номера разрядов, 8 — основание системы счисления

2.9.   2C16 и 2D16

 2.10.

Система счисления

1016

10

1110

10011 10 101        12 1110

                                                                          11020                                                       12                    11

                                111                                                      21                13                12

1000  1022   20       13

1001  11100 21 14 10 1010 12 101 22 20 11 1011  13 102 23 21 12 1100 14110 зо 22

13                 1104   15111 31       23

14                 1110   16112 32       24

15                 17120 33 зо 16 10000 20 10 121 100 31

                 17                 10001                 21                    11                   122                  101                   32

2.11. 1010002, 2203, 408, C016, 220004, 1007. 2.12. 100112, 20223, 5178, 9FF16, 31134, 46

2.13. 100002, C016, 22223, 1ОА16. 2.14. Пары меньшее—большее:

             2.15. з, 1, 2          2.16. з, 2, 1

             2.17. 23145 - 2 . 53+ 3 .          1 .          4 •         250 + 75 + 5 + 4 = 33410

10100112_ 26 + 2 4 + 2 1 + 1 = 64 + 16 + 2 + 1 = 8310

 2 • 16 2 + 10 • 16 1 + 11 = 512 + 160 + 11 = 68310

2.18. 10101102 - 8610, 210203 - 19510, 5268 = 34210, ЗСЕ16 = 97410, 30214 - 20110, 2567 - 13910

2.19. 6 целых и 5 в остатке. 2.20. 4 целых и З в остатке. 2,21. О целых и 7 в остатке

2.22. 53 = 1101012. 2.23. 202 - 13025.

2.24. 57 = 1110012, 65 = 21023, 335 = 5178, 202 = СА1б, 198 = 30124,139 = 2567

2.25. З, 1, 2. 2.26. 2158. 2.27. 3748, 1268. 2.28. 4, 1 (группами по 4), 2, З. 2.29. 6016

2.30. 3FC16, 75Е1б 2.31, З, 1, 2. 2.32. 1110011002. 2.33. 1100000112, 0110101012.

2.34. З, 2 (из 4 разрядов, 4 разряда), 1. 2.35. 1101001001112.

2.36. 1110010000112, 1010000011002. 2.37. 4; 2.38. 4; 2.39. 1; 2.40. з; 2.41. з; 2.42. 4; 2.43. 6;

2.44. 2; 2.45. з; 2.46. 4; 2.47. 6; 2.48. 4; 2.49. з; 2.50. 5, 21; 2.51. 6, 14, 22; 2.52. 7, 16, 25;

2.53. 8, 33; 2.54. 5, 13, 21; 2.55. з, 7, 21; 2.56. 4, 6, 8, 12, 24; 2.57. 11, 22; 2.58. 9, 27;

2.59. 13, 26; 2.60. 4; 2.61. з; 2.62. 5; 2.63. 4; 2.64. 4; 2.65. 1218; 2.66. 1000101101$,

2.67. 1031$, 2.68. 17В16•, 2.69. 2; 2.70. 4; 2.71. 2; 2.72. з; 2.73. 1; 2.74. 10101112;

2.85. 2008; 2.86. 2013; 2.87. 2013; 2.88. 11; 2.89. 7; 2.90. 6; 2.91. 8; 2.92. 13; 2.93. 33;

2.94. 99; 2.95. 28; 2.96. 58; 2.97. 60.

З. Кодирование информации

3.1. 6); 3.2. все; 3.3. 60; 3.4. 512; 3.5. 384; 3.6. 4; 3.7. 1; 3.8. 4; 3.9. 375; 3.10. З; 3.11. З;

3.12. З; 3.13. 4; 3.14. 2; 3.15. 1; 3.16. а-5, 6-6, в-1, г-4, д-2, е-з•, 3.17. а-з, 6-4, в-5, г-2, Д-1; 3.18. 1; 3.19. 4; 3.20. 2; 3.21. 4; 3.22. 1; 3.23. 8; 3.24. 5; 3.25. 7; 3.26. 16; 3.27. 8; 3.28. 2; 3.29. 256; 3.30. 65536; 3.31. з; 3.32. 1536; 3.33. 256; 3.34. 320; 3.35. 8; 3.36. 48; 3.37. 2048;

3.38. 1024; 3.39. 32; 3.40. 8; 3.41. 128; 3.42. З; 3.43. З; 3.44. 2; 3.45. УУУОУ•, 3.46. НЛЛМ;

3.47. тптп; 3.48. 1; 3.49. з; 3.50. 112; 3.51. 350; 3.52. 10; 3.53. 15; 3.54. 50; 3.55. 80.

4. Основы логики

4.3. а) А = 1, В - 1; 6) А

4.7. а) 1; 6) 2. 4.8. а) 1; 6) З; в) 2; г) 4. 4.9. а) 4; 6) 4; в) 2; г) З. 4.10. а) З; 6) З.

4.11. а) 4; 6)3•, в) 2; г) 4. 4.12. а)3•, 6) 4; в) 1; г) 4. 4.13. а) З; 6) 15. 4.14. а) 2; 6) 4.

            4.15 • а) 0001; 6) 1000. 4.16. а) 12; 6) 1. 4.17. а) 10; 6) 14; в) 16; г) 68.        

4.18. 4. 4.19. а) 2; 6) З; в) 4;

4.20. з; 4.21. 1; 4.22. з; 4.23. 4; 4.24. 2; 4.25. 1; 4.27. 251; 4.28. 117; 4.29. о; 4.30. 128;

4.31. 1254.32. 14; 4.33. 18; 4.34. 13; 4.35. 11.

5. Алгоритмизация и программирование

            5.1. а) 25; 6) 8                 5.2. а) + •                                                   5.10. а)         - 1)/2; 6)          - п)

5.14. а) 2; 6) 1. 5.15. а) 2; 6) 345. 5.17. а) 12211; 6) 21211. 5.18. а) 2, А8, Н4; 6) 2, G1, РЗ

5.19. а) 513; 6) 10. 5.20. а) 2; 6) 1. 5.21. а) 1; 6) 1. 5.24. а)

Область

Условие 1

Условие 2

Условие З

( <=2 — х)

Условие 4

( >= х*х)

Программа

выведет

Область обрабатывается верно

 

да

нет

 

 

 

нет

в

да

нет

 

 

 

нет

с

да

нет

 

 

 

нет

 

да

нет

 

 

 

нет

 

да

да

да

нет

не принадлежит

да

 

да

да

да

да

принадлежит

да

 

да

да

да

нет

не принадлежит

нет

н

да

да

нет

 

 

нет

 

нет

 

 

 

 

нет

 

нет

 

 

 

 

нет

Программа:

if (у<=1) and (у>=0) and (and  then write ( принадлежит ' )

write ( ' не принадлежит ' )

5.24. 6)

Область

Условие 1

Условие 2

Условие з

Программа выведет

Область обрабатывается ве но

 

нет

 

 

 

нет

в

да

да

да

п инадлежит

да

с

да

да

да

п инадлежит

нет

 

да

да

нет

не п инадлежит

нет

 

да

нет

 

 

нет

Программа:

if (х>=—2) and (х<=1) or (х>_—4) and (х<=7) then write ( ' принадлежит ' )

write ( ' не принадлежит ' )

5.26. 15, „5.27. 24, 5.28. 72;

5.29.

2) 9 (также верным является любое натуральное число, имеющее цифру 9);

З) Вместо строки “ К: ; ” должна быть строка ” К: ; “ (вместо О может быть любое отрицательное число), вместо строки ”while N >= 10 do” должна быть строка ”while N > 0 do” (также возможно исправление ”while N >= 1 do”);

5.30.

2) 53 (верным является любое натуральное число, имеющее наименьшую цифру не первую);

З) Вместо строки ”while N > 9 do” должна быть строка ”whi1e N > О do” (также возможно исправление ”while N >= 1 do");

5.31.

1)  22;

2)  1 (верным также является любое натуральное число, имеющее последнюю цифру О, а первую больше 1);

З) Вместо строки ” К: mod 10; ” должна быть строка  вместо строки ”while N > 1 do” должна быть строка ”while N > О do” (также возможно исправление ”while N >= 1 do“);

5.32.

2) 10 (также верным является любое натуральное число, имеющее цифру О);

З) Вместо строки ' К: “ должна быть строка ”k:=1; ”, вместо строки ”k:=k*N mod 10; ” должна быть строка ”k:=k* (N mod 10) ; “

5.33. 60, 5.34. 47, 5.35. 28.; 5.37. 8, 5, 4, 6, 8, 5, 4, з, 2; 5.38. 4, 2, з, 4; 5.39. 2, 4, 2, 6, з;

5.40. 5, з, 1, 1, 2, о, 1; 5.41. з; 5.42. 1; 5.43. 61; 5.44. 175; 5.45. 930; 5.46. 337;

5.47. 46; 5.48. 46; 5.49. 1100; 5.50. 58; 5.51. 1100; 5.52. 1110; 5.53. 13; 5.54. 21; 5.55. 20;

5.56. 28; 5.57. 60; 5.58. 65; 5.59. 44; 5.60. 77877; 5.61. а) 8; 6) 778; в) 788.

6. Информационные модели

6.1. 2; 6.2. з; 6.3. з; 6.4. 3,5; 6.5. 11; 6.6. 17:25; 6.7. 18:15; 6.8. 16:30; 6.9. 16:20;

6.10. 14:10; 6.11. 25; 6.12. 30; 6.13. 24.

7. Определение выигрышной стратегии игры (Анализ и построение дерева игры)

7        Л. См. полное решение и ответ в тексте.

7.2. Выигрывает Ваня. Для доказательства рассмотрим неполное дерево игры, оформленное в виде таблицы, где в каждой ячейке записаны пары чисел, разделенные запятой. Эти числа соответствуют количеству камней на каждом этапе игры в первой и второй кучках со-

ответственно.

Стартовая

позиция

ход (Пети), все варианты хода

II ход (Вани), выигрышные ходы

III ход (Пети), все варианты хода

IV ход (Вани), выигрышные ходы

12,3

36,3

Выигрыш Вани

6,3

6,9

18,9

54,9

8,9

8,27

6,27

Выигрыш Вани

6,11

6,33

4,9

6,9

Те же ва ианты III—IV ходов

 

12,6

36,6

Выигрыш Вани

14,6

42,6

12,18

36,18

12,8

36,8

Таблица содержит все возможные варианты ходов первого игрока (Пети). Из нее видно, что при любом ходе первого игрока у второго (Вани) имеется ход, приводящий к победе.

7.4. 1а) S = 21...30. Петя должен добавить в кучу 10 камней и выиграть. Для S < 20 невозможно одним ходом получить в куче больше 30 камней.

16) S = 20. Куда бы ни ходил Петя (20 + 1 = 21 или 20 + 10 = 30), Ваня должен добавить в кучу 10 камней и выиграть.

2. S = 10 и S = 19. Своим первым ходом Петя должен получить в куче 20 камней (10 + 10 = 20 или 19 + 1 = 20). При любом ответном ходе Вани (20 + 1 — 21 или 20 + 10 = 30) Ваня должен добавить в кучу 10 камней и выиграть.

З. S = 18. Если Петя добавит в кучу 10 камней (18 + 10 = 28), Ваня тоже добавит в кучу 10 камней и выиграет (28 + 10 = 38).

Если же Петя добавит в кучу 1 камень (18 + 1 19), Ваня тоже добавит в кучу 1 камень (19 + 1 = 20). При любом ответном ходе Пети (20 + 1 = 21 или 20 + 10 = 30) Ваня должен добавить в кучу 10 камней и выиграть. Рассмотрим дерево игры:

18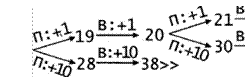

В этом дереве в каждой позиции, где должен ходить Петя, разобраны все возможные ходы, а для позиций, где должен ходить Ваня — только ход, соответствующий стратегии, которую выбрал Ваня.

7.6.

1а. S = 29...57. Петя Должен удвоить число камней во второй куче.

16. Единственный подходящий вариант (S = 28) не подходит, т.к. при первом ходе Пети «+1 к первой куче» получается ситуация (8, 28), из которой нельзя выиграть одним ходом. Числа, меньшие 28, тоже не подходят (при S = 27 Добавление 1 камня во вторую кучу приводит к (7, 28), из которой не выиграть). Аналогично, можно такое показать для каждого меньшего S.

2. S = 28. Первым ходом Петя Должен Добавить 1 камень в первую кучу (получится

(8, 28)). При любом ответном ходе Вани Петя Должен удвоить вторую кучу и выиграть.

з. S = 27.

Рассмотрим Дерево игры:

в: 28*2

(7,27)

В Дереве рассмотрены все возможные ходы Пети и ответные ходы Вани, соответствующие выигрышной стратегии. Знаком ”>>” обозначены позиции, в которых партия заканчивается.

7.8.

Задание 1.

Из позиции (10, 26) можно получить (11, 26), (20, 26), (10, 27), (10, 52). Во всех случаях сумма камней в кучах меньше 63, однако удвоение второй кучи приводит к выигрышу (в сумме будет не менее 63 камней). Значит, позиция (10, 26) — проигрышная и выигрышную стратегию имеет Витя. Он выигрывает своим первым ходом.

Из позиции (12, 25) можно получить (13, 25), (24, 25), (12, 26), (12, 50). Во всех этих случаях сумма камней в кучах также меньше 63 и удвоение второй кучи приводит к выигрышу. Значит, позиция (12, 25) — также проигрышная и выигрышную стратегию имеет Витя. Он выигрывает своим первым ходом. Задание 2.

Для каждой из рассматриваемых позиций существует ход, который приводит в проигрышные позиции, рассмотренные в задании 1.

(6, 25) -> (12, 25), (9, 26) -> (10, 26), (10, 25) -> (10, 26).

Значит, эти позиции — выигрышные. Выигрышную стратегию имеет Паша. Его первый ход нами указан. Паша выигрывает на своем втором ходу. Игра из позиций (10,26) и (12,25) рассмотрена в задании 1. Задание З.

В позиции (9, 25) выигрышную стратегию имеет Витя. Если Паша первым ходом пойдет в (10, 25) или (9, 26), Витя пойдет в (10, 26) и выиграет своим вторым ходом. Стратегия его игры описана в заданиях 1 и 2.

Если же Паша первым ходом пойдет в (18, 25) или (9, 50), Витя выиграет своим вторым ходом, удвоив количество камней во второй куче.

           Рассмотрим дерево игры:      

В этом дереве рассмотрены все возможные ходы Паши и соответствующие им ходы Вити согласно выигрышной стратегии. Знаком >> обозначены позиции, в которых партия закан- чивается.

8.         Файловая система компьютера

8.5. а) З; 6) 1. 8.6. а) З; 6) 4. 8.7. а) З; 6) 4; в) 2; г) З. 8.8. а) З; 6) З; в) 2; г) 4. 8.9. а) 2;

9.         Электронные таблицы

9.1.                     все. 9.2. а), б), г), д), з). 9.3. б), в), д), з), к). 9.4. а—З, 6—9, в—5, г— 11, д—1, е—1О, ж—4, 3—7, и—б, к—8, л—2. 9.5. а), б), г), д), е), ж), з), и) (т.е., все, кроме в). 9.6. а—4, 6—5, в—1, г—З, д-2. 9.7. а)1•, 6) З; в) 4; г) 12; д) 9; е) 4; ж) 18; з) 256. 9.8. а) О; 6) 7; в) 10; г) 2,5; д) 6. 9.9. 4; 9.10. 2; 9.11. 1; 9.12. -11; 9.13. 8; 9.14. 52; 9.15. -$B2+D$2; 9.16. =$С1-А$З•, 9,17. =$A$4+D1•, 9.18. * $М; 9.19. 2; 9.20. 4; 9.21. 1; 9.22. 1; 9.23. а), в); 9.24. 1; 9.25. б), в);

9.26. 6; 9.27. 8.

10.  Базы данных

10.1.                все; 10.2. а-4, 6-6, в-з, г-5, д-1, е-2; 10.3. З; 10.5. 5; 10.7. 4; 10.8 а-2, 6-3, в-1;

10.9. бгва•, 10.10. 1; 10.11. З; 10.12. 2; 10.13. 4; 10.14. 1; 10.15. З; 10.16. З; 10.17. 4;

10.18. 210; 10.19. 205; 10.20. 1; 10.21. з; 10.22. 2; 10.23. 4.

11.  Сетевые технологии

11.1.                а), 6) в), г), е), ж), з); 11.2. З; 11.3. ГБВА•, 11.4. БВГА; 11.5. БАГВ; 11.6. все;

11.7. ЖГБВАЕД•, 11.8. ГЖАВДЕБ•, 11.9. ДВГАЕБЖ; 11.10. ЭКГДВБЕА; 11.11. 321;

11.12. 2341; 11.13. 1234; 11.14. 2314; 11.15. 4312; 11.16. 4312; 11.17. 2134; 11.18. 2143;

11.19. а) 4500; 6) 2200; в) 4400; г) 1100. 11.20. МВВ•, 11.21. 240; 11.22. 224; 11.23. 192.

КОНТРОЛЬНЫЕ ВАРИАНТЫ ЭКЗАМЕНАЦИОННОЙ РАБОТЫ

Инструкция по выполнению работ“

Экзаменационная работа состоит из двух частей, включающих в себя 27 заданий. Часть 1 содержит 23 задания с кратким ответом. Часть 2 содержит 4 задания с развёрнутым ответом.

На выполнение экзаменационной работы по информатике и ИКТ отводится З часа 55 минут (235 минут).

Ответы к заданиям 1—23 записываются в виде числа, последовательности букв или цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов N2 1.

ким   Бланк Ответ: 23

Задания 24—27 требуют развёрнутого решения. В бланке ответов N2 2 укажите номер задания и запишите его полное решение.

Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, или капиллярной, или перьевой ручек.

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов, Жедшеж успеха!

В экзаменационных заданиях используются следующие соглашения.

1. Обозначения для логических связок (операций):

а) отрицание (инверсия, логическое НЕ) обозначается -л (например, —4);

Ь) конъюнкция (логическое умножение, логическое И) обозначается л (например, А л В) либо & (например, А & В);

с) дизъюнкция (логическое сложение, логическое ИЛИ) обозначается v (например, А v В) либо (например А В);

d) следование (импликация) обозначается (например, А —» В);

е) тождество обозначается (например, А В). Выражение А В истинно тогда и только тогда, когда значения А и В совпадают (либо они оба истинны, либо они оба ложны);

f) символ 1 используется для обозначения истины (истинного высказывания); символ О — для обозначения лжи (ложного высказывания).

2. Два логических выражения, содержащих переменные, называкугся равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А В и (— А) v В равносильны, а А v В и А л В неравносильны (значения выражений разные, например, при А = 1, В = О).

З. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, А л В v С л D означает то же, что и А) л В) (С л D).

Возможна запись А л В л С вместо (А л В) л С. То же относится и к дизъюнкции: возмощна запись А v В С вместо (А v В) v С.

4. Обозначения Мбайт и Кбайт используются в традиционном для информатики смысле — как обозначения единиц измерения, чьё соотношение с единицей «байт» выражается степенью двойки.

Вариант 1

Часть 1

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код: А—ОО, Б—О1, В—1ОО, Г—1О1, Д—110. Укажите кратчайшее кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Ответ:

Каждое из логических выражений А и В зависит от одного и того же набора 6 переменных. В таблицах истинности обоих выражений в столбцах значений стоит ровно по 5 единиц в каждой таб- лице. Каково минимально возможное число единиц в столбце значений таблицы истинности выражения Av—B?

Ответ:

Во фрагменте базы данных представлены сведения о родственных отношениях. Определите на основании приведенных данных числовой идентификатор (ID) внука Дени К. Д.

                                                                             Таблица 1                                                Таблица 2

ID

Фамилия И.О.

пол

 

ID Родителя

ID Ребенка

42

Бабенко А.Е.

м

53

42

82

Сорт А.К.

 

21

42

53

Марченко Е.Е.

м

71

53

21

ирта О.Б.

ж

14

53

26

Гано И.Е.

эк

 

14

71

Камо Е.А.

м

78

14

14

дени К.Д.

ж

71

26

34

Ивенко .Я.

м

14

26

78

Исава Г.А.

ж

26

82

57

м

57

78

Ответ:

Сколько единиц в двоичной записи шестнадцатеричного числа E5F016?

Ответ:

Между населенными пунктами А, В, С, D, Е, F построены дороги, протяженность которых приведена в таблице (если ячейка пуста — дороги нет).

Определите длину кратчайшего пути между пунктами А и Р. Ответ:

6. На вход алгоритма подается натуральное число N. Алгоритм строит по нему новое число V следующим образом.

1.               Строится двоичная запись числа N.

2.               К этой записи дописываются справа еще два разряда по сле дующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

 

 

 

 

 

 

 

 

 

20

 

13

А2+$С$1

25

41

 

 

17

 

50

 

Бейсик

Python

лм S ,

WHILE S

WEND

PRINT

N AS INTEGER

95

10

5

while s <= 95 :

print (п)

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа У.

Укажите такое наименьшее число N, для которого результат работы алгоритма больше 57. В ответе это число запишите в двоичной

системе счисления. Ответ:

    7.      Дан фрагмент электронной таблицы

Формулу из ячейки В2 скопировали в ячейку СЗ так, что числовое значение ячейки СЗ стало отличаться от числового значения ячейки В2. Каково стало числовое значение ячейки СЗ?

Ответ:

Запишите число, которое будет напечатано в результате выполнения следующей программы. Для Вашего удобства программа представлена на пяти языках программирования.

Алго итмический язык

 

Паскаль

алг нач цел п, п S нц пока s <= 95

S п кц вывод п кон

 

 

var S , п: integer; begin S        о; п while s <= 95 do begin       

п end; writeln (п) end.

 

 

Си

int main ()

{ int s       о; while (Б <= 95) { S printf , п) ; return 0;

S + 10; п

Паскаль

Си

procedure f (n:integer) ; begin writeln (п) ; if п < 5 then begin f (n+1) ; f (п+2) end end;

#include void f (int п)

printf , п) ; if (п<5)

f (n+1) ; f (n+2) ;

Ответ:

Какой минимальный объем памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024 х 512 пикселов при условии, что в изображении могут использоваться 8 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Ответ:

Андрей составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует свое кодовое слово. В качестве кодовых слов Андрей использует 5-буквенные слова, в которых есть только буквы О, Р, Е, Л, причем буква Р появляется ровно 1 раз. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Андрей?  Ответ:

Ниже на пяти языках программирования записана рекурсивная функция (процедура) Р.

Бейсик

 

Алго итмический язык

FUNCTION

PRINT N

IF N E 5 THEN

F(N+1)

F(N+2)

END IF

END FUNCTION

 

алг цел А (цел п) нач вывод п если п < 5 то

все кон

 

hon

def Г (п) :

print (п) if     5 :

 

 

 

 

 

 

 

н

О

94

137

216

219

248

251

255

 

 

 

 

 

 

 

 

128

168

255

8

127

О

17

192

Чему равна сумма выводимых на экран чисел при вызове F(1)?.

Ответ:

12.       В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть 1Р-адреса узла сети относится к адресу сети, а какая — к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и 1Р-адрес. Адрес сети получается в результате применения поразрядной конъюнкции к заданному 1Р-адресу узла и маске.

По заданным 1Р-адресу узла и маске определите адрес сети.

                IP —адрес узла:     251.137.219.94

                 Маска:                     255.255.248.0

Выберите из приведенных в таблице чисел четыре Элемента IPадреса и запишите в качестве ответа нужном порядке соответствующие им буквы. Точки писать не нужно.


Пример.

Пусть искомый 1Р-адрес 192,168.128.0, и дана таблица

В этом случае правильный ответ будет записан в виде: HBAF Ответ:

13.       Репетиционный экзамен сдают 9 потоков по 100 человек в каждом. Каждому из них выделяют специальный код, состоящий из номера потока и номера в потоке. При кодировании этих номеров участников проверяющая система использует минимально воз можное количество бит, одинаковое для каждого участника, отдельно для номера потока и номера в потоке. При этом для записи кода используется минимально возможное и одинаково целое количество байтов. Каков объем информации в байтах, записанный устройством после регистрации 80 участников? В ответе укажите только число.

Ответ:

14.       Исполнитель Редактор получает на вход строку цифр и преобразовывает ее. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки цифр.

А) заменить (v, w).

Эта команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Капример, выполнение команды заменить (222, 34) преобразует строку 77222277 в строку 7734277.

Если в строке нет вхождений цепочки v, то выполнение команды заменить (v, w) не меняет эту строку.

Б) нашлось (v).

Эта команда проверяет, встречается ли цепочка v в строке исполнителя Редактор. Если она встречается, то команда возвращает логическое значение «истина», в противном случае возвращает значение «ложь». Строка исполнителя при этом не изменяется.

Цикл

ПОКА условие последовательность команд КОНЕЦ ПОКА выполняется, пока условие истинно.

В конструкции

ЕСЛИ условие

ТО команда1

ИНАЧЕ команда2 КОНЕЦ ЕСЛИ выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Какая строка получится в результате применения приведенной ниже программы к строке, состоящей из 80 идущих подряд цифр 7? В ответе запишите полученную строку.

НАЧАЛО

ПОКА нашлось (777) ИЛИ нашлось (888)

ЕСЛИ нашлось (777)

                                                                                   ТО заменить (777, 8)           

ИНАЧЕ заменить (888, 7)

КОНЕЦ ЕСЛИ

КОНЕЦ ПОКА КОНЕЦ

Ответ:

15. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

д

Ответ:

Паскаль

Си

min [1] ; for i:=2 to 100 do if A[i] <min then k:=i;

К        1; min = А [1] ; for (1=2      if (A[i] <min) k=i;

Бейсик

Алго итмический язьпе

К        1 min = А (1) FOR ТО 100 IF А (1) < min THEN к

ENDIF

NEXT i

min : =А [1] нц для i от 2 до 100 если А [ET<min

то k:=i все кц

 

hon

К      1 min = А [1] for i in range (2, 101) : -if A[i] < min: k=i

 

запросу:

[10, 24]. которого

Паскаль

 

Си

var х, Ь, М: integer; begin read1n (х) ;

м   о; whi1e do begin м if х mod 2 0 then begin

- L + 1; end; х  х div 2; end; write1n (Ы ; write end.

 

void main ( )

int х, L, М; scanf ( 6d

whi1e (х > 0)

if (x % 2 ! — 0)

х

  printf ( ”          ,

Бейсик

 

Алгоритмический язык

DIM Х, L, М AS

INPI.JT х

WHILE

IF Х МОР 2

ENDIF х

WEND

PRINT

PRINT м

INTEGER

THEN

 

алг нач цел х, Ь, м ввод х

м нц пока х > 0 м если mod (х, 2) то

все х  div (х, 2) кц вывод L, нс, М кон

 

 

Python

х     int (input ( ) )

м whi1e х do

if х %

L=L+1 х print (L) ptint (М)

 

 

Чему будет равно значение переменной К после выполнения данной программы, если известно, что массив был заполнен четными двузначными числами, расположенными в порядке неубывания от начала к концу массива. Ответ:

20.        Получив на вход число х, алгоритм печатает два числа L и М. Укажите наименьшее из таких чисел х, при вводе которых алгоритм печатает сначала 4, а потом 8.

Ответ:

IlaCKaJ1b

CH

 

function f (n: integer) : integer; begin if n 0 then f

f             f (n—l) end; var k, i : integer;

BEGIN read In (k) ;

while f (i) >k do i:=i—l; write (i) ;

END.

int f (int n)

if (n   0) return 0;

return n+n

void main ( )

int k, i; scanf ("%d" , & k) ;

i  12; while (f (i) >k)

print f ("%d", i) ;

-1) ;

Beicmc

AaropHTMHqecKHi *3b1K

DIM K, 1 AS INTEGER

INPUT K

1   12

WHILE F (1) > K

1  1

WEND

PRINT 1

FUNCTION

ELSE

     F   N+N-I +

END FUNCTION

ajll'

Hag

I-len k, i BBOÄ k i  12

HI-I I'10Ka F (i) i  i   1

BblBOÄ i

KOH ajll'        F (men

Haq

 0 no

3HaT-Æ

MHaqe

3HaT--Æ

BCe

KOH

> k

n)

n+n    

Python

def f (n) : if n return

              return         f(n—l)

k    int (input ( ) ) i   12 while f (i) >k

print (i)

21.        Hume Ha narrn H3b1Kax npHBezxeHa nporpaMMa. OnpemeJIØTb, npn CKOJ1bKHX pa3JIHt1Hb1X 3HaqeHHax h nporpaMMa negaeraerr TOT %-ce pe3YJ1bTaT, LITO n npø k = 90 (BKmoqaa k = 90).

Omæm:

22.        У исполнителя Калькулятор две команды:

1.  Прибавь З,

2.  Умножь на 2.

Первая из них увеличивает число на экране на З, вторая — удваивает его.

Программа для Калькулятора это последовательность команд. Сколько есть программ, которые число 1 преобразуют в  число 41?

для записи ответов на задания этой части (24—27) используйте бланк ответов NQ 2. Запишите сначала номер задания (24, 25 и т.д.), а затем полное решение. Ответы записывайте четко и разборчиво.

Паскаль

Си

const п       4; var i, х • integer; min, К    integer; begin о; min        о; for i         1 to п do begin read (х) ; if х mod 2 <> 0 then begin

К К 1; if min х then

min х end end; if К > 0 then writeln (min)

write1n ( 'NO end.

#inc1ude <stdio.h> #define п 4 void main (void)

int i, х; int min, К;

К    о; min        о; for (i

scanf   &х) ; if (х %        0)

if (min < х) min

if (К > 0) printf , min) ; printf  ;

Ответ:

23.        Сколько существует различных наборов значений логических переменных х1, .х2, хз, х4, х5, У1, уз, У4, У5, которые удовлетворяют всем перечисленным ниже условиям?

(Х 1 Х2) л (Х2 хз) л ( хз Х4) л (Х4 Х5) - 1— (-И И) л (-И уз) л (-И У4) л (-И У5)

(У1 х 1) л (У2 х2) л (уз хз) л (У4 х4) л (У5 х5) = 1

Ответ:

Часть 2

24.        Требовалось написать программу, которая считывает с клавиатуры п натуральных чисел (например, п = 4), каждое из которых не больше 1000, и выводит на экран минимальное нечетное из них. Если таких чисел нет, программа должна вывести на экран «NO».

Программист торопился и написал программу неправильно.

Бейсик

 

Алгоритмический язык

CONST п     4

К min

FOR     - 1 то п

INPUT х

IF х mod 2 <> О THEN

К

IF min < х THEN min х

END IF

END IF

NEXT

IF К > О THEN

PRINT min

ELSE      

       PRINT

END IF

 

алг нач цел 4 цел i, х цел min, К

К min  нц для i от 1 до ввод х если mod (х,

      1 если min min  х

все все кц если К > 0 то вывод min иначе вывод ”NO”

все кон

п

0 то

то

 

Python

п  4 К о; min о; for i in range (1, п х int (input ( ) ) if     

if. min < х min   х if К > 0 print ( min)

print ( ”NO” )

1) :

Последовательно выполните следующее.

 1. Укажите, что выведет на экран программа при вводе последова-• тельности чисел 1 2 З 4.

2, Приведите пример такой последовательности из п допустимых чисел, при котором программа работает верно.

З. Исправьте все ошибки в программе. Для этого для каждой ошибки приведите строку, которая написана неверно, и строку, на которую ее нужно заменить, чтобы программа работала верно.

25.        Дан целочисленный массив из 40 элементов. Элементы массива могут принимать целые значения от 1 до 99. Опишите на русском языке или на одном из языков программирования алгоритм, позволяющий найти и вывести количество элементов массива, сумма цифр которых не делится на З.

Паскаль

Си

const N=40; var а: array [1 . .N] of integer; i, ј , К, s : integer; begin for i:=1 to N do readln (a [ i ] ) ;

#inc1ude <stdio.h> #define N 40 void main (void)

{int a [N] ; int 1, ј, К, s ; for (1=0; i<N; scanf ( 6f

Бейсик

Алго итмический язык

N=40

DIM A(N) AS INTEGER

DIM 1, О, К, S AS INTEGER

FOR                   1 ТО N

INPUT А (1)

NEXT

END

алг

нач цел N=40 целтаб а [1 цел • i, ј , К, s нц для i от 1 до N ввод a [i]

кц

кон

Python

40 i            None

None

К      None

[int (input () ) for i in range (N) ]

Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается

не использовать часть из них.

В качестве ответа вам необходимо привести фрагмент программы, который должен находиться на месте многоточия.

Два игрока, Паша и Витя, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый  ход делает Паша. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней  в куче в два раза. Например, пусть в одной куче 10 камней, а в  другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за Один ход можно получить любую из четырех позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 61. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую пози цию, что в кучах всего будет 61 или больше камней.

Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию  игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. Например, при начальных позициях (З, 29) и (1, 30) выигрышная стратегия есть у Паши. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.

Задание 1. Для каждой из начальных позиций (4, 28), (6, 27) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.

Задание 2. Для каждой из начальных позиций (4, 27), (5, 27), (6, 26) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните,  почему эта стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. 

Задание З. Для начальной позиции (5, 26) укажите, кто из игро- ков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведет к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте деревО в виде рисунка или таблицы.

27. На вход программе подается набор символов, заканчивающийся символом О (в программе на языке Бейсик символы можно вводить по одному в строке, пока не будет введен ноль, или считывать данные из файла). Ноль в этом наборе единственный. Напи шите эффективную, в том числе и по используемой памяти, программу (укажите используемую версию языка программирования, например Borland Pascal 7,0), которая будет составлять из всех имеющихся цифр (кроме завершающего последовательность нуля) минимальное число, состоящее ровно из трех повторяющихся одинаковых групп цифр ненулевой длины. Составленное число следует вывести на экран или в файл.

В случае невозможности составить такое число, программа должна вывести «NO».

Например, пусть на вход подаются следующие символы: fd7s22hg 547h2j 47х5 540

В данном случае программа должна вывести:

245724572457

ID

Фамилия И.О.

Пол

 

ID Ребенка

34

Арно В.А.

ж

18

34

18

Жуйко А.И.

м

61

 

61

Кирта У.Т.

ж

96

18

96

Вирк Я.М.

ж

47

18

47

Иваненко И.Л.

м

29

47

29

Калпен Л.В.

м

56

47

56

Ирита Е.О.

ж

 

29

84

Кименко З. Т.

ж

15

29

72

Олинг К.Л.

ж

29

72

15

Гираб В.А.

м

56

72

Вариант 2

Часть 1

По каналу связи передаются сообщения, содержащие только 4 буквы А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова: А: ООО, Б: 1, В: 001. Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Ответ:

Каждое из логических выражений А и В зависит от одного и того же набора из 6 переменных. В таблицах истинности этих выражений нет ни одной одинаковой строки. Сколько строк таблицы истинности для выражения Av—B содержат 1 в столбце значений?

Ответ:

отношениях. Определите на основании приведенных данных числовой идентификатор (ID) бабушки Иваненко И.Л.

                                                          Таблица 1                                                   Таблица 2

Ответ:

Сколько единиц в двоичной записи восьмеричного числа 701308?

протяженность которых приведена в таблице (если ячейка пуста — дороги нет).

Определите длину кратчайшего пути между пунктами А и F.

Ответ:

строится новое число по следующим правилам.

1.                Складываются первая и вторая, а также третья и четвертая цифры исходного числа.

2.                Полученные два числа записываются друг за другом в порядке возрастания (без разделителей).

Пример. Исходное число: 4853. Суммы: 4 + 8 = 12; 5 + зультат: 812.

Укажите наибольшее число, в результате обработки которого автомат выдаст число 1517.

Ответ:

Формулу- из ячейки В2 скопировали в ячейку СЗ так, что числовое значение ячейки СЗ стало отличаться от числового значения ячейки В2. Каково стало числовое значение ячейки СЗ?

Ответ:

граммы:

Бейсик

 

Алго итмический язык

DIM

1

S      105

WHILE

WEND

PRINT

AS INTEGER

> 5

1

 

алг нач цел i, s

105 нц пока s > 5

кц вывод i кон

 

 

hon

1 105 whi1e

print (i)

S > 5 2

1

 

Паскаль

Си

procedure f (п: integer) ; begin writeln (п) ; if п > З then begin f (n—1) ; f(n—3) end end;

#inc1ude <stdio.h> void f (int п)

printf    п) ; if (n > З)

f (n—1) ; f (n—3) ;

Ответ:

Производится одноканальная (моно) звукозапись с частотой дискретизации 4 кГц и 32-битным разрешением. Запись длится 10 минут, ее результаты записываются в файл, сжатие данных не производится. Определите приблизительно, размер получившегося файла (в Мбайтах). В качестве ответа укажите ближайшее к размеру файла целое число кратное З.

Ответ:

Все 4-буквенные слова, составленные из букв П,  Т, записаны в алфавитном порядке.

Вот начало списка:

1.      пппп

2.      ПППР

з. пппс 4. пппт

5. ППРП

На каком месте в списке стоит первое слово, начинающееся с буквы Р?

Ответ:

Ниже на пяти языках программирования записана рекурсивная функция (процедура) Р.

Бейсик

Алго итмический язык

FUNCTION

PRINT N

 THEN

END IF

END FUNCTION

алг F (цел п) нач вывод п если п > З то

все кон

 

оп

def Е (п) :

print (п) if п > З:

1)

- 3)

 

Определите сумму чисел, которых выведет программа при вызове F(5).           

Ответ:

12.       В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть 1Р-адреса узла сети относится к адресу сети, а какая к адресу самого узла в этой сети. Обычно маска записывается по тем же правилам, что и 1Р-адрес. Адрес сети получается в результате применения поразрядной конъюнк- ции к заданному узла и маске.

                   По заданным узла и маске определите адрес сети.         

IP — адрес узла: 153.236.189.51

                  Маска:                     255.255.224.0

А

B C I) E F' G I--I

о

51

153

160

189

224

236

255

А В С

 

 

 

G r-I

128

168

255

8

127

о

17

192

Выберите из приведенных в таблице чисел четыре элемента IPадреса и запишите в качертве ответа нужном порядке соответствующие им буквы. Точки писать не нужно.

Пример.

Пусть искомый 1Р-адрес 192.168.128.0, и дана таблица

В этом случае правильный ответ будет записан в виде: HBAF

Ответ:

13.       Репетиционный экзамен в СПб сдают 20 потоков по 50 человек в каждом. Каждому из них выделяют специальный код, состоящий из номера потока и номера в потоке. При кодировании этих номеров участников проверяющая система использует минимально возможное количество бит, одинаковое для каждого участника, отдельно для номера потока и номера в потоке. При этом для за-

вверх

вниз

влево

вправо

сверху свободно снизу свободно слева свободно справа своОцно

писи кода используется минимально возможное и одинаково целое количество байтов. Каков объем информации в байтах, записанный устройством после регистрации 70 участников? В ответе укажите только число.

Ответ:

14.       Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости включает 4 командыприказа и 4 команды проверки условия. Команды-приказы:

При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх Т, вниз ! , влево е, вправо -9. Если РОБОТ начнет движение в сторону находящейся рядом с ним стены, то он разрушится, и программа прервется.

Другие четыре команды проверяют истинность условия отсутствия стены 'у каждой стороны той клетки, где находится РОБОТ:

Цикл:

ПОКА < условие > последовательность команд КОНЕЦ ПОКА выполняется, пока условие истинно.

В конструкции

ЕСЛИ < условие >

ТО команда1

ИНАЧЕ команда2

КОНЕЦ ЕСЛИ выполняется команда1 (если условие истинно) или команда2 (если условие ложно).

Сколько клеток приведенного лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную ниже программу, РОБОТ уцелеет и остановится в клетке F6?

НАЧАЛО

ПОКА < снизу свободно ИЛИ справа свободно >

ЕСЛИ < справа свободно > ТО вправо КОНЕЦ ЕСЛИ

ПОКА < снизу свободно > вниз КОНЕЦ ПОКА

КОНЕЦ ПОКА

КОНЕЦ

Ответ:

15.       На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных  путей из города А в город К?

                                                       Б           д               и

Ответ:

                                                                                                                         2016         2015

16.       Значение арифметического выражения: 9 + З — 2 — записали в системе счисления с основанием З. Сколько цифр «2» содержится в этой записи? Ответ:

17.       В языке запросов к поисковому серверу для обозначения логической операции «ИЛИ» используется символ 1, а для логической

операции «И» — &. В таблице приведено количество страниц, которое находит поисковая система по каждому запросу.

Запрос

Количество найденных страниц (в тысячах)

А б зы

84

ыни

47

Тыквы

19

А б зы & Тыквы

12

Тыквы & ыни

 

А б зы Тыквы

ЫНИ

120

Какое количество страниц (в тысячах) будет найдено по запросу:

Арбузы & Дыни?

Ответ:

ных целых чисел т и п. Так, например, 11 & 6 = 10112 & 01102 00102 - 2.

Для какого наибольшего неотрицательного целого числа А формула

тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной х)?

Ответ:

сами от 1 до 100. Ниже представлен фрагмент программы, обрабатывающей данный массив.

 

Бейсик

Алго итмический язык

К            1

ENDIF

NEXT i

то 100

А [К] THEN

нц для •i от 2 до 100 если A[i] >=А[К] то

все кц

 

 

thon

К     1 for i in range (2, 101) :

k=i

 

Паскаль

Си

 

var х, L, М: integer; begin read1n (х) ; о; о; whi1e        do begin м if х mod 2    0 then begin

1;

end; х х div 2; end; write1n write (М) ;

# inc1ude<stdio . h> void main ()

int х, L, М; scanf (”%d” , о;

whi1e (х > 0)

      if (x % 2    0)

1;

х printf

L, М) ;

Бейсик

Алго итмический язык

DIM Х, ь, М AS INTEGER INPUT х

WHILE

             IF Х MOD 2               о ТНЕГЧ

ENDIF х   х \ 2

WEND

PRINT

PRINT м

алг нач цел х, L, м ввод х

м нц пока х > 0 м если mod (х, 2) то

все х   div (х, 2) кц вывод L, нс, М кон

Чему будет равно значение переменной после выполнения данной программы, если известно, что массив был заполнен четными двузначными числами, расположенными в порядке неубывания от начала к концу массива.


Ответ:

Получив на вход число х, алгоритм печатает два числа L и М. Укажите наибольшее из таких чисел х, при вводе которых алгоритм печатает сначала 5, а потом 8.

 

hon

x   int (input ( ) ) L  o M  o while x > 0

if

x print (L, M)

 

IlaCKaJ1b

 

function f (n: integer) : integer; var i, s : integer; begin

for i:=l to n do s:=s+n; f:=s end; var k, i : integer;

BEGIN read In (k) ; i:=l; while f (i) k k do

write (i) ;

END.

int f (int n)

int i, s; s     o; for (i=l • i<=n s                 n; return s; void main ( )

int k, i; scan f ("%d" , &k) ; i 1; while (f (i) < k)

     printf( 6d  i ) ;

 

Beicmc

AaropHTh•nmecKHi "3b1K

DIM K, 1 AS INTEGER

INPUT

1  1

WHILE

  1 1 + 1

WEND

PRINT 1           

FUNCTION F (N)

DIM 1, S AS INTEGER

S           

FOR 1   1 TO N

S

NEXT 1 s

END FUNCTION

ajll'

Haq

I-ten k, i BBOÄ k

     i    1

HIA 110Ka F (i)

1

KLI

BblBOÄ i

KOH ajll' I-xen F (uejl n) zen-i, s

Haq

    s   o;

           I s           

      3Hat-1     S

KOH

k

no n

Omeem:

21. Huxce Ha nsrrn fl3b11-cax npHBeAeHa nporpaMMa. OnpeaeJIHTb, npn CKOJ1bKHX pa3J1nqHb1X 3HaT-1eHnax k nporpaMMa neqaTaeT TOT xe pe3YJ1bTaT, YTO npn k — 60 (BKJIK)T-1aa k = 60).

Ответ:

У исполнителя Калькулятор две команды:

1.      Прибавь З,

2.      Умножь на 2.

Первая из них увеличивает число на экране на З, вторая — удваивает его.

Программа для Калькулятора — это последовательность команд.

Сколько есть программ, которые число 2 преобразуют в число 40? Ответ:

Сколько существует различных наборов значений логических переменных х1, х2, ..., х8, х9, которые удовлетвориют всем перечисленным ниже условиям?

V .t2 л хз = 1

-1 1

Ответ:

Часть 2

24. Требовалось написать программу, которая считывает с клавиатуры п натуральных чисел (например, п =4 ), каждое из которых не больше 1000, и выводит на экран сумму тех из них, которые не кратны З. Если таких чисел нет, программа должна вывести на экран «NO».

Программист торопился и написал программу неправильно.

 

 

llamcaJ1b

CH

const n 4; var i, x integer; sum, k integer; begin k    1 ; sum o; for i 1 to n begin read (x) ; if x mod begin

sum  sum end end; if k > 0 then writeln (k)

write In ( 'NO end.

do

0 then

x

# include <stdio.h> #define n 4

void main (void)

int i, x; int sum, k; k    1 ; sum = 0; for (i  1 ;                            

scanf ("%d" , &x) if (x 3  0)

                sum   sum

if (k > 0) print f ( "  , k) ;

print f ("NO\n") ;

Beiicmc

 

Aaro HTMnqecKHi $13b1K

CONST n   4 k   1 sum

FOR 1  1 TO n

INPUT x

IF x mod 3 < >

sum — sum +

END IF

NEXT 1

IF k > O THEN

PRINT k

ELSE

PRINT

END IF

o THEN

x

ajll' Haq

               I-xen n      4

I-xen i, x I-xen sum, k k     1

BBOÄ x mod (x, 3)

                sum    sum +

BCe

KLI

> 0 TO

BblBOA

J/1Haqe

BblBOA

KOH

n

0

x

hon

k   1 sum = 0 for i in range (l,n+l) : x — int (input ( ) ) if x%3 ! =

sum sum + x if k > 0 print (k) ;

print ( NO'

Последовательно выполните следующее.

1.                Укажите, что выведет на экран программа при вводе последовательности чисел 1 2 З 4.

2.                Приведите пример такой последовательности из п допустимых чисел, при котором программа работает верно.

З. Исправьте все ошибки в программе. Для этого для каждой ошибки приведите строку, которая написана неверно, и строку, на которую ее нужно заменить, чтобы программа работала верно.

Дан целочисленный массив из 30 элементов. Элементы массива могут принимать значения от О до 1000. Опишите на русском языке или на одном из языков программирования алгоритм, который находит и выводит сумму элементов самой длинной возрастающей последовательности подряд идущих элементов массива. Если таких последовательностей несколько, вывести сумму элементов самой первой такой последовательности.

Паскаль

Бейсик

const

N=30; var а: array integer;

тах, sum: integer; begin for i:=1 to N do read1n (а

end.

N=30

DIM A(N) AS INTEGER

DIM 1, Ј, К, МАХ, SUM AS

INTEGER

FOR                 1 ТО N

INPUT A(I) NEXT Л

END

си

Естественный язык

#include <stdio .h> #define N ЗО void main (void) {int a[N] ; int 1, ј , К, та х, sum; for (i=O; i<N; i++) scanf (” % d” ,

Объявляем массив А из 30 элементов .

96ъявляем целочисленные пе— ременные 1, о, К, МАХ, SUM. В цикле от 1 до 30 вводим элементы массива А с 1—го по 30—й.

hon

i        None

None К None а [int (input ( ) ) for i in range (N) ]

Исходные данные объявлены так, как показано ниже. Запрещается использовать переменные, не описанные ниже, но разрешается не использовать часть из них.

В качестве ответа вам необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен находиться на месте многоточия. Вы можете записать решение также на другом языке программирования (укажите название и используемую версию язьжа программирования, например Borland Pascal 7.0) или в виде блок-схемы. В этом случае вы должны использовать переменные, аналогичные переменным, используе мым в алгоритме, записанном на естественном языке, с учетом синтаксиса и особенностей используемого вами языка программирования.

26.           Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу 1 камень или 2 камня или увеличить количество камней в куче в 2 раза. Например, имея кучу из 6 камней, за один ход можно получить кучу из 7, 8 или 12 камней. У каждого игрока, чтобы де- лать ходы, есть неограниченное количество камней. Игра завершается в тот момент, когда количество камней в куче становится не менее 28. Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 28 или больше камней.

В начальный момент в куче было S камней, 1 S 27.

Говорят, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.

Выполните следующие задания. Во всех случаях обосновывайте свой ответ.

1.                 а) При каких значениях числа S Петя может выиграть первым ходом? Укажите все такие значения.

б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.

2.                 Укажите два значения S, при которых у Пети есть выигрышная стратегия, причем Петя не может выиграть за один ход, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для указанных значений S опишите выигрышную стратегию Пети.

З. Укажите такое значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, но при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом. Для указанного значения S опишите выигрышную стра- тегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На

ребрах дерева указывайте, кто делает ход, в узлах — количество камней в куче.

27.           На вход программе подаются сведения о неуспеваемости ученика за весь период его обучения в школе, за каждый месяц в отдельности. В первой строке сообщается количество месяцев (N), которые проучился ученик. В каждой из следующих N строк находится информация о количестве двоек, которые получил ученик за соответствующий месяц в течение всего периода обучения в формате: <Месяц> <Год> <Число двоек>, где <Месяц> — полное название месяца, <Год> год обучения, не раньше 1990 (может быть позже), <Число двоек> — число от О до 999.

Пример: апрель 2006 12

Порядок строк произвольный. Возможно, некоторые месяцы ученик не учился по причине болезни или каникул, и они отсутствуют в списке. Возможно, некоторые годы ученик также не учился (находился в академическом отпуске).

Напишите эффективную, в том числе и по используемой памяти, программу (укажите используемую версию языка программирования, например Borland Pascal 7.0), которая будет выводить на экран годы, в которые ученик учился лучше, чем в первый год своего обучения.

Если нет таких лет, необходимо вывести об этом сообщение.

Считается, что ученик учится тем лучше, чем меньше у него двоек.

Пример входных Данных:

6 январь 1995 12 февраль 1997 20 март 2001 5 апрель 2001 6 май 2005 10 июнь 2003 18

Пример выходных Данных:

2001

                                                                   2005        

Другой пример входных Данных: 6 январь 1995 9 фйраль 1997 20 март 2001 5 апрель 2001 6 май 2005 10 июнь 2003 18

Пример выходных Данных:

Нет таких лет

ОТВЕТЫ К КОНТРОЛЬНЫМ ВАРИАНТАМ ЭКЗАМЕНАЦИОННОЙ РАБОТЫ

Вариант 1

.М2 задания

Ответ

Лё задания

Ответ

.М2 задания

Ответ

1

11

11

64

21

19

2

59

12

GCDA

22

23

з

42

13

160

23

21

4

9

14

8877

 

5

11

15

32

6

1110

16

5

7

24

17

23

8

50

18

14

9

192

19

1

10

 

20

135

24

Содержание верного ответа и указания по оцениванию

(допускаются иные формулировки ответа, не искажающие его смысла)

Решение использует запись программы на Паскале. Дбпускается использование программы на трех других языках.

1.              Программа выведет число: З.

2.              Пример последовательности, для которой программа работает правильно: 2 2 З 2. Замечание для проверяющего. Вместо минимального нечетного программа находит максимальное нечетное. Значит, верным будет любая последовательность 4-х натуральных чисел, которая либо не содержит нечетных элементов, либо этот элемент единственный, либо все нечетные элементы равны друг другу. З. В программе есть две ошибки.

Первая ошибка: неверная инициализация переМенной min. Строка с ошибкой:

min := О;

Верное исправление: min:= 1001;

Допускается любое числб, больше и равное 1000. Вторая ошибка: неверная проверка на минимальность. Строка с ошибкой:      if min < х then Верное исправление:          if min > х then

 

 

Указания по оцениванию

Баллы

Обратите внимание! В задаче требовалось выполнить четыре действия:

1) указать, что выведет программа при конкретной входной последовательности;

2 казать п име последовательности, п и кото ой п ог амма аботает п авильно;

 

 

З) исправить первую ошибку; 4) исправить вторую ошибку.

Для проверки правильности выполнения п. 2) нужно формально выполнить исходную (ошибочную) программу с входными данными, которые указал экзаменуемый, и убедиться в том, что результат, выданный программой, будет таким же, как и для правильной

программы.

Для действий З) и 4) ошибка считается исправленной, если выполнены оба следующих условия:

а) правильно указана строка с ошибкой;

б) указан такой новый вариант строки, что при исправлении другой ошибки получается п авильная п г амма

 

 

Выполнены все четыре необходимых действия, и ни одна верная строка не указана в качестве ошибочной

З

 

Не выполнены условия, позволяющие поставить З балла. Имеет место одна из следующих ситуаций:

а) выполнены три из четырех необходимых действий. Ни одна верная строка не указана в качестве ошибочной;

б) выполнены все четыре необходимых действия. Указано в качестве ошибочной не более одной ве ной ст оки

2

 

Не выполнены условия, позволяющие поставить 2 или З балла. Выполнены два необходимых действия из четы ех

1

 

Не выполнены условия, позволяющие поставить 1, 2 или З балла

 

 

Максимальный балл

 

 

 

Содержание верного ответа и указания по оцениванию допускаются иные о мули овки ответа, не искажающие его смысла)

 

На языке Паскаль

 

К      о; for i 1 to N do if (a [i] mod 10 + a [ i] div 10) mod З <> 0 then

К writeln (К) ;

 

На алго итмическом языее

 

к .

нц для i от 1 до N если (mod (a [i] , 10) +div (a [i] , 10)

то

К все

кц вывод К

 

На языке Бейсик

 

  FOR               1 ТО N

IF (A(I) MOD 10+A(I) \  THEN

ENDIF

NEXT

PRINT К

На языке СИ

 

for (i=0; i<N; i++)

printf

 

На языке

thon

 

а [int (input ( ) ) ] for i in range (0, N) :

print (К)

 

 

Указания по оцениванию

Баллы

 

Предложен правильный алгоритм, выдающий верное значение.

Допускается запись алгоритма на другом языке, использующая аналогичные переменные. В случае, если язык программирования использует типизированные переменные, описания переменных должны быть аналогичны описаниям переменных на естественном языке. Использование нетипизированных или необъявленных переменных возможно только в случае, если это допускается языком программирования, при этом количество переменных и их идентификаторы должны соответствовать условию задачи. В алгоритме, записанном на языке программирования, допускается наличие отдельных синтаксических ошибок, не искажающих замысла авто а п ог аммы

2

 

В любом варианте решения может присутствовать не более одной ошибки из числа следующих.

Не инициализируется или неверно инициализируется переменная (например, присваивается начальное значение, не равное О).

Неверно осуществляется выделение цифр числа.

На нечетность проверяется не сумма цифр числа, а что-то другое.

Неверно осуществляется проверка неделимости на три.

В сложном условии вместо логической операции «И» используется логическая операция «или».

Неверно осуществляется накопление количества элементов в цикле (например,

ОтсуТствует вывод ответа.

Используется переменная, не объявленная в разделе описания переменных.

Не указано или неверно указано условие завершения цикла.

Индексная переменная в цикле не меняется (например, в цикле while) или меняется неверно, или отсутствует цикл.

Неве но асставлены опе ато ные скобки

1

 

Ошибок, пе ечисленных выше, две или больше, или алгоритм с о мули ован неверно.

 

 

Максимальный балл

2

 

26

Содержание верного ответа и указания к оцениванию

(допускаются иные формулировки ответа, не искажающие его смысла)

Задание 1. В начальных позициях (4, 28), (6, 27) выигрышная стратегия есть у Вити. При начальной позиции (4, 28) после первого хода Паши может получиться одна из следующих четырех позиций: (5, 28), (8, 28), (4, 56), (4, 29). Каждая из этих позиций содержит менее 61 камня. При этом из любой из этих позиций Витя может получить позицию, содержащую не менее 61 камня, удвоив количество камней во второй куче. Для позиции (6, 27) после первого хода Паши может получиться одна из следующих четырех позиций: (7, 27), (12, 27), (6, 28), (6, 54). Каждая из этих позиций содержит менее 61 камня. При этом из любой из этих позиций Витя может получить позицию, содержащую не менее 61 камня, удвоив количество камней во второй куче. Таким образом, Витя при любом ходе Паши выигрывает своим первым ходом.

Задание 2. В начальных позициях (4, 27), (5, 27) и (6, 26) выигрышная стратегия есть у Паши. При  начальной позиции (4, 27) он должен первым ходом получить позицию (4, 28), из начальных позиций (5, 27) и (6, 26) Паша после первого хода должен получить позицию (6, 27). Позиции (4, 28) и (6, 27) рассмотрены при разборе задания 1. В этих позициях ВЫИГРЫШНая стратегия есть у игрока, который будет ходить вторым (теперь это Паша). Эта стратегия описана при разборе задания 1. Таким образом, Паша при любой игре Вити выигрывает своим вторым ходом.

Задание З. В начальной позиции (5, 26) выигрышная стратегия есть у Вити. После первого хода Паши может возникнуть одна из четырех позиций: (6, 26), (5, 27), (10, 26) и (5, 52). В позициях (10, 26) и (5, 52) Витя может выиграть одним ходом, удвоив количество камней во второй куче. Позиции (6, 26) и (5, 27) были рассмотрены при разборе задания 2. В этих позициях у игрока, который должен сделать ход (теперь это Витя), есть выигрышная стратегия. Эта стратегия описана при разборе задания 2. Таким образом, в зависимости от игры Паши Витя выигрывает на первом или на втором ходу. В таблице изображено дерево возможных партий при описанной стратегии Вити. Заоючительные позиции (в них выигрывает Витя) выделены жирным шрифтом.

 

 

Положения после очередных ходов

Исходное положение

1-й ход Паши (разобраны все ходы, указана полученная позиция)

1-й ход Вити (только ход по стратегии, указана полученная позиция)

2-й ход Паши (разобраны все ходы, указана полученная позиция)

2-й ход Вити (только ход по стратегии, указана полученная позиция)

(5, 26) Всего:

31

(5, 26+1)  (5, 27)

Всего: 32

(5+1, 27)

Всего:

(6, 27)

33

(6+1, 27) - (7, 27)

Всего: 34

(7, 27*2) - (7, 54)

Всего: 61

    (6, 27+1)     (6, 28)

Всего:

(6, 28*2) = (6, 56)

Всего.• 62

(6*2, 27) = (12, 27)

Всего: 39

(12, 27*2)    (12, 54)

Всего: 66

      (6, 27*2) ¯        54)

Всего: 60

(6, 54*2) - (6, 108)

Всего: 114

(5+1, 26) = (6, 26)

Всего: 32

(6, 26+1)

Всего:

(6, 27)

33

(6+1, 27) = (7, 27)

Всего:

(7, 27*2) = (7, 54)

Всего: 61

    (6, 27+1)     (6, 28)

Всего:

(6, 28*2) - (6, 56)

Всего: 62

    (6*2, 27)       (12, 27)

Всего: 39

(12, 27*2)    (12, 54)

Всего: 66

     (6, 27*2)     (6, 54)

Всего: 60

(6, 54*2) - (6, 108)

Всего: 114

(5*2, 26) - (10, 26)

Всего: 36

(10, 26*2) - (10, 52)

Всего: 62

 

 

(5, 26*2) - (5, 52)

Всего: 57

    (5, 52*2)       (5, 104)

Всего.• 109

 

 

Примечание. Дерево всех партий может быть таюке изображено в виде ориентированного графа. Вершины дерева, соответствующие одной и той же позиции, на рисунке могут быть «склеены». Важно, чтобы множество полных путей в графе находилось во взаимно однозначном соответствии с множеством партий, возможных при описанной в решении стратегии.

Примечание. В некоторых позициях у Вити есть и другой способ выигрыша: например, в позиции (6, 54) можно добавить один камень в любую кучу. То, что это не указано, не является ошибкой. Экзаменуемый не должен указывать все возможные выигрышные стратегии

27

Основные элементы правильного ответа:

Программа читает все входные данные только один раз, запоминая в целочисленном массиве из 9 элементов, сколько раз встречается соответствующая цифра во входных данных.

После этого проверяется, что все ненулевые элементы этого массива равны трем. Если это условие не выполняется или все элементы массива равны нулю, то выводится «NO».

В противном случае три раза подряд выводится упорядоченная по возрастанию группа цифр, состоящая из всех ненулевых цифр исходной строки. Пример возможного решения (на С++):

#include <iostream> using namespace std;

int main ( )

int пит [10] ; / / из соображений наглядности элемент пит [0] не задействован char с; for (int i=1; i<=9; i++) пит [1] 0; / / инициализация cin >> с; while (с ! =

if пит [с— '/ / подсчет цифр cin >> с;

bool yes =false; for (int 1=1; i<=9; i++)

/ / проверка, есть ли в строке хотя бы одна цифра if (num[i] > yes true; break;

if (yes)

      for (int i=1;            i++)

/ / проверка, кратно ли трем количество вхождений каждой встреченной цифры if ( (num[i] > 0) && (пит yes false; break;

if (yes) / / вывод результата

for (int ј=1; ј<=З; Ј++) for (int 1=1;

for (int k=l; k<= num [i]  cout << i;

else cout << "NO" ; cout << ' \ n' ; return 0;

llpu.uep peuenua (Ha mcnaccugecxo.% Ilacxane):

program c4 (input, output) ; var num: array [ ' 1 ' ' 9' ] of integer; i, c: char; j , k: integer; yes: boolean;

begin for i : = ' 1 ' ' 9 ' do num [i]0; { MHM1.xmaJ11,f3aLIMA } read (c) ; while c < > ' 0 ' do begin if ' 1 ' ) and) then num [c] num [c] +1; { nomcqe rr um@p} read (c)

       yes    false;

while (not yes) and (ido begin

{ rpoBepra, eCTb B cmpore XOTA 661 0ÄHa } if num [i] > 0 then yes true; succ (i) end; if yes then begin

             while yes and (i       do

{ npoBepKa, rpaTH0 JIM TEEM KOJImqeCTBO BXoxmeH>fi Kaxmoj•r BCC'pegeHHOM LIM@Pb1} begin if (num [i] and (num [i] mod 3 <>0) then yes false; succ (i) end end; if yes then {BblBOA pe3YJ1bTa rra} begin for J . to 3 do for i : = '1' to '9' do for k:=l to num [i] div 3 do write (i) end else write ('NO' ) ; write In; end .

Ilpu.uep 60.3Æ0%Hoeo pezuuu.g (Ha Beücuxe, xo.ununamop FreeBASIC

Dim num (9) As Integer

Dim i As Integer

Dim j As Integer

Dim k As Integer

Dim yes As Integer

Dim c As String

For      To 9

           Num (i)       0    MH1.•fUmaJIM3aLIMA

Next i

Input c

Do While

' nomcqe rr um@p if (c>" 0" ) And 9" ) Then Num (Asc (c) —Asc (' — Num (Asc (c) — Asc ( "

Input c Loop

yes For    To 9

' npoBepKa, ecTb   B cæpoKe XOTA 661 OAHa

If num (i) > 0 Then yes  1

Exit For

End If Next i

If yes   1 Then

           For     To 9

' rrpoBepKa, KpaTH0 JIM 'lt peM KOJIMgeCTBO BXomueHmjf Ka n,KÄOV1 Bc rrpeqeHH0i 1-1M$Pb1 If (num (i) And (num (i) Mod 3<> 0) Then yes

Exit For

End If

Next i End If c=

If yes  1 Then ' BblBOA pe3YJ1bTaæa

                For      To 3

                              For     To 9

For k=l To num (i) / 3 c=c+Chr$ (i+Asc

Next k

Next

Next j

Print c

Else

Print "NO"

End If

Вариант 2

«М задания

Ответ

.М2 задания

Ответ

Л) задания

Ответ

1

010

11

15

21

27

2

 

12

CGDA

22

17

з

84

13

14 О

23

50

4

5

14

23

 

5

9

15

19

6

9896

16

2014

7

27

17

18

8

51

18

11

9

9

19

100

10

65

20

224

24

Содержание верного ответа и указания по оцениванию

(допускаются иные формулировки ответа, не искажающие его смысла)

 

Решение использует запись программы на Паскале. Допускается использование программы на трех другйх языках.

1.                Программа выведет число: 4.

2.                Пример последовательности, для которой программа работает правильно: 1 1 1 2. Замечание для проверяющего. В конце программы выводимое на экран значение переменной будет на 1 больше, чем количество введенных чисел, не кратных трем. То есть верной будет любая последовательность, у которой сумма чисел, не кратных трем равна количеству этих чисел +1. Так как числа натуральные, это возможно, только если в последовательности есть числа, не кратные трем, одно из них = 2, остальные = 1. З. В программе есть две ошибки.

Первая ошибка: неверная инициализация переменной К. Строка с ошибкой:   

Верное исправление:

Вторая ошибка: неверный вывод на экран (выводится не та переменная). Строка с ошибкой: writeln(k);

Верное исправление:

writeln(sum);

 

Указания по оцениванию

Баллы

Обратите внимание! В задаче требовалось выполнить четыре действия:

1)                 указать, что выведет программа при конкретной входной последовательности;

2)                 указать пример последовательности, при которой программа работает правильно; З) исправить первую ошибку; 4) исправить вторую ошибку.

Для проверки правильноети выполнения п. 2) нужно формально выполнить исходную ошибочную) п ог амм с входными данными, кото ые казал экзамен емый, и бедиться

 

 

в том, что результат, выданный программой, будет таким же, как и для правильной программы.

Для действий З) и 4) ошибка считается исправленной, если выполнены оба следующих условия:

а) правильно указана строка с ошибкой;

б) указан такой новый вариант строки, что при исправлении другой ошибки получается п авильная прог амма

 

 

 

Выполнены все четыре необходимых действия, и ни одна верная строка не указана в качестве ошибочной

з

 

 

Не выполнены условия, позволяющие поставить З балла. Имеет место одна из следующих ситуаций:

а) выполнены три из четырех необходимых действий. Ни одна верная строка не указана в качестве ошибочной;

б) выполнены вёе четыре необходимых действия. Указано в качестве ошибочной не более одной ве ной ст оки

2

 

 

Не выполнены условия, позволяющие поставить 2 или З балла. Выполнены два необходимых действия из четырех

1

 

 

Не выполнены условия, позволяющие поставить 1, 2 или З балла

 

 

 

Максимальный балл

з

 

25

{ Число элементов в текущей последовательности. Изначально считаем, что последовательность состоит из одного (первого) элемента } sum:=a [1] ; { Сумиа элементов текущей последовательности тах :=0; { Наибольшая длина возрастающей последовательности }

for i to п do if a [i ] >а [i-1] begin

        К:=К+1    

else     Если begin if К>тах then

        begin              

           тах : =k;      

            • .=sum       

begin тах : ;

end; write (ј) ; { Вывод

{ Перебираем все пары соседних элементов } then Если последовательность продолжает возрастать }

{ Увеличиваем ее сълплу элементов

{ Увеличиваем счетчик длины последовательности }

последовательность прекратила возрастать }

{ Проверяем, не является ли закончившаяся последовательность длиннее текущего максуплума } Если да:

Меняем текуц.ийт макспиум }

Заповшанаем суингу его элементов }

Устанавливаем длину новой последовательности равной 1 Суттиа элементов этой последовательности (пока) }

На случай, еа.тм самая дјмнная последовательность находится в конце массива, проверим еще раз текущий макспиум

ответа на экран


26

Содержание верного ответа и указания к оцениванию

(допускаются иные формулировки ответа, не искаэкающие его смысла)

1а) S = 14...27. Петя должен увеличить количество камней в куче в 2 раза и выиграть. Для S < 14 невозможно одним ходом получить в куче 28 и более камней.

16) S = 13. Куда бы ни походил Петя (13 + 1       14, 13 + 2 = 15 или 13*2 = 26), Ваня должен увеличить количество камней в куче в 2 раза и выиграть.

2. S = 11 и S = 12. Своим первым ходом Петя должен получить в куче 13 камней (11 + 2 = 13 или 12 + 1 13). При любом ответном ходе Вани (13 + 1 - 14, 13 + 2 = 15 или 13*2 = 26), Петя должен увеличить количество камней в куче в 2 раза и выиграть.

З. S = 10. Если Петя удвоит количество камней в куче (10*2 = 20), Ваня тоже удвоит количество камней в куче и выиграет (20*2 = 40).

Если же Петя добавит в кучу 1 камень или 2 камня (10 + 1 — 11 или 10 + 2 — 12), Ваня должен довести количество камней в куче до 13 (11 + 2 13 или 12 + 1 13). При любом ответном ходе Пети (13 + 1 14, 13 + 2 = 15 или 13*2 = 26), Ваня должен увеличить количество камней в куче в 2 раза и выиграть. Рассмотрим дерево игры:

в:*2

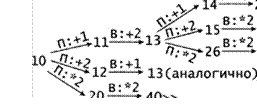
В этом дереве в каждой позиции, где должен ходить Петя, разобраны все возможные ходы, а для позиций, где должен ходить Ваня — только ход, соответствующий стратегии, которую выбрал Ваня.

27

Программа сначала читает из входных данных информацию о количестве двоек за каждый месяц. Эту информацию она накапливает в целочисленном массиве, элементы которого соответствуют годам обучения (от 1990 до 2010). В другом массиве (логическом), элементы которого пронумерованы так же, накапливается информация о том, учился ли ученик в соответствующий год. Одновременно программа находит начальный и конечный год обучения ученика. После этого программа проходит по массиву, начиная с года, следующего за первым годом обучения, и для лет, когда ученик учился, проверяет, меньше ли число двоек, полученных учеником в этот год числа двоек в первый год обучения. Если результат сравнения оказывается верным, программа Выводит номер соответствующего года на экран. Одновременно с этим подсчитывается количество таких лет. В конце программы, если количество этих лет оказывается равно нулю, выводится сообщение о том, что таких лет нет.

Программа на языке Паскаль:

var а array[1990. . 2010] of integer; f array[1990. . 2010] of Ьоо1еап;

1, К, п, first, 1ast, year, пит 1 п teger; ch     char; begin

{ Обнуляем массивы а и f for 1990 to 2010 do begin

{ Число двоек в год обучения } f[i) :=false; { Обучался ли в этот год } end;

first:=2011; { Первый год обучения } 1ast:=1989; { Последний год обучения } { Считываем количество месяцев обучения read1n (п) ;

{ для каждого месяца обучения } for i 1 to п do begin

{ Отбрасываем название месяца } repeat read (ch) until ch=' ' до первого пробела } { Считываем год и количество двоек } read1n (year, пит) ;

{ Увеличиваем число двоек в этом году а [year] :=а [year] +num;

{ Запоминаем, что в этот год ученик учился f[year] :=true;

{ Проверяем, не раньше ли этот год текущего первого года } if year<first then first: =year;

{ Проверяем, не позже ли этот год текущего последнего года } if year>1ast then

1ast :=year

К: =0; { Обнуляем счетчик числа лет обучения } { Перебираем все года от второго до последнего for year:=first+1 to 1ast do

{ Если в этот год ученик учился и при этом учился лучше, чем в первый год } if f[year] and (a[year] [first] ) then begin writeln (year) ; { Выводим номер года на экран

К:=К+1 { Увеличиваем счетчик числа лет обучею end; if then { Если нет таких лет обучения } write1n ( 'HeT таких лет ' )

Программа на языке Бейсик:

DIM а (20) AS INTEGER

DIM f (20) AS INTEGER

DIM i, К, first, 1ast, year, пит AS INTEGER

DIM s AS STRING

REM Обнуляем массивы а и f

                                                      FOR i              о то 20

REM Число двоек в ” год обучения           1990” a (i) REM Обучался ли в этот год

NEXT

REM Первый год обучения

first — 2011 REM  rom 06yqeHMA

last - 1989

REM CYMTb1BaeM KOJImqeCTBO MeCA1.xeB oöyqeHYIA

INPUT n

REM    Kaxnoro MecHua 06yqeH1/1A

FOR i   1 TO n

LINE INPUT s

REM OTÖpaCb1BaeM Ha 3BaHme MecA1.xa

MID$ (s, 1, 1) i    1

REM Ao nepB01'0 npoöena WHILE NOT (c$ i c$ = MID$ (s, i, 1)

WEND

REM BbaneJIAeM rom year = VAL

REM BblmeJIAeM I-conmqeCTBO ABoeK num = VAL (MID$ (s, i +6, LEN ( 1+5 ) ) ) REM Y Bej1hH1,1BaeM I-IHCJIO ABoeK B STOM romy a (year-1990) — a (year—1990) + num

REM 3ar10MMHaeM, gno B STOT rom yqeHYIK yqmncg f (year 1-990) ) 1

REM flpoBepneM, He paHbl.ue JIM STOT rom

REM rreæymero nepB01'0 roma IF year < first THEN first —year END IF

REM FIpoBepAeM, He nosxe JIM 3TOT rom

REM rreKY1.ue1'0 nocJ1e11Hero noma IF year>last THEN last   year END IF

NEXT i

REM OÖHYJIÆM cqe rrqYIK qmcna Jle rr k

REM Flepe6mpaeM BCe roma 0T BTOPOFO no nocneAHero

FOR year   first +1 TO last

REM ECJIVI B STOT rom yqeHMK yumJICA m

REM 3TOM y %4JICA nyqwe, geM B nepBb11.%1 rom

IF f (year-1990)=1 AND a  (first —1990) THEN

REM BblBOÄVIM HOMep roma Ha 3KpaH

PRINT year

REM Y  cqe'T t4MK qmcna nem 06yqeHMA

NEXT year

REM ECJIYI Hen rraKMX Jle rr oöyqeH1,1A

IF     THEN

PRINT 't HeT rraKUX neT"

END IF

END

Справочное издание

Крылов Сергей Сергеевич

Ушаков Денис Михайлович

ЕГЭ

ИНФОРМАТИКА

ТЕМАТИЧЕСКИЕ ТЕСТОВЫЕ ЗАДАНИЯ

Издательство «ЭКЗАМЕН»

Гигиенический сертификат

РОСС RU. АЕ51. Н 16678 от 20.05.2015 г.

Главный редактор Л. Д. Лаппо

Редактор Г. А. Лонцова

Технический редактор Л. В. Павлова

Корректоры Г. М. Морозова, Н. Е. Жданова

Дизайн обложки Л. В. Демьянова

Компьютерная верстка К. А. Реутова, А. В. Толокевич

107045, Москва, Луков пер., д. 8. www.examen.biz

E-mail: по общим вопросам: info@examen.biz; по вопросам реализации: sale@examen.biz  тел./факс 8 (495) 641-00-30 (многоканальный)

Общероссийский классификатор продукции ок 005-93, том 2; 953005   книги, брошюры, литература учебная

Отпечатано в соответствии с предоставленными материалами в ООО «ИПК Парето-Принт», г. Тверь, www.pareto-print.ru

По вопросам реализации обращаться по тел.: 8 (495) 641-00-30 (многоканальный).


[1] следующие подряд идущие до единицы 2010 — 4 = 2006 нулей превратились в единицы, а единица, разделявшая нули, превратилась в ноль. Добавляя 1, получаем lOO...OOOl 1 ... lO...012. Всего 1 + 2006 + 1 = 2008 единиц.

[2] 6

Ответ: 2008.

[3] .85. Сколько единиц содержится в двоичной записи значения выражения:       20132010

[4] .86. Сколько единиц содержится в двоичной записи значения выражения: 4 2015 + 22014            7?

[5] .87. Сколько единиц содержится в двоичной записи значения выражения: 420152014

[6] натуральное число N (N<10) и выводится на экран сумма цифр этого числа. Программист торопился и написал программу неправильно.

СОЗДАНО РАЗРАБОТЧИКАМИ ФИПИ ИНФОРМАТИКА iiii iiiiiiiii i iiiiiiii iiiiiiiiiiiiiiiii ! *0tt Е ГЭ ИНФОРМАТИКА Теория Тематические задания Книга содержит множество тематических заданий для отработки каждого элемента содержания Файловая система компьютера 5 Желаем успеха! ДИАГНОСТИЧЕСКИЙ З. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество З. База данных о продажах некоторого торгового предприятия состоит из трех связанных таблиц Таблица продаж: На какую сумму (в тысячах рублей) были заключены договоры о поставках в Бейсик Паскаль 1024 Бейсик Алгоритмический язык Производится двухканальная (стерео) звукозапись с частотой дискретизации 4 кГц и 64- Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится На месте преступления были обнаружены четыре обрывка бумаги Сколько клеток приведенного лабиринта соответствуют требованию, что, выполнив предложенную ниже программу (и не разрушившись), Запрос Количество найденных страниц (в тысячах) НАЧАЛО ПОКА снизу свободно вниз ПОКА справа свободно вправо Бейсик Паскаль L, М : integer; begin read1n ( х ) ; о ; м о ; whi1e х do begin м В программе описан одномерный целочисленный массив Ниже представлен фрагмент программы, записанный на разных языках программирования, в котором значения элементов сначала задаются, а затем меняются S end; var k, i : integer; begin read Omeem: Hnxce Ha 11flTH fl3b11-cax lipHBeAeHa rrporpararaa Ответ: У исполнителя Калькулятор две команды: 1 Паскаль Си var х , sum, Бейсик Паскаль None Ј None К None а [int (input ( ) ) for i 1 п range (N) ] Последовательно выполните следующее Укажите, что выведет на экран программа при вводе числа 1234 В качестве ответа необходимо привести фрагмент программы (или описание алгоритма на естественном языке), который должен на- ходиться на месте многоточия На вход программе подается набор символов, заканчивающийся сиТволом ОТВЕТЫ К ДИАГНОСТИЧЕСКОМУ ВАРИАНТУ Обратите внимание! В задаче требовалось выполнить четыре действия: 1) указать, что выведет программа при конкретной входной последовательности; 2) указать пример последовательности, при которой программа работает… O; i<N; х=х+1; (f10at) у / х ; printf , Содержание верного ответа и указания к оцениванию (допускаются иные формулировки ответа, не искажающие его смысла) 1а) Ьоо 1 yes =fa1se; for (int i=1; i<=9; i++) / / проверка, есть ли в строке хотя бы одна цифра if yes — true; break;… NO' ) ; write In; Ilpumep 603MO%HOeo peuuua (Ha Основные понятия Информация первичное понятие, не имеющее общепринятого, классического определения I — количество информации в сообщении, t — время передачи сообщения Загадано число от 1 до 100. Загадавший на все вопросы отвечает только «Да» или «Нет» Репетиционный экзамен в школе сдают 125 человек Вася передает Пете сообщение, состоящее только из символов (заглавных и строчных) латинского алфавита, пробелов и знаков препинания ( Ответ: 1.18. Скорость передачи данных через равна 128 Количество информации при этом будет рассчитываться, конечно, по тем же формулам, что описано выше Если необходимо закодировать количество сообщений, не являющееся целой степенью числа В некоторой организации решили присвоить каждому сотруднику уникальный код, состоящий из символов латинского алфавита (используются все 26 заглавных букв) и цифр Рекомендация. Из-за необходимости передать

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также

Мы используем Cookies

Продолжая использовать наш сайт, вы соглашаетесь с политикой использования Cookies. Это файлы в браузере, которые помогают нам сделать ваш опыт взаимодействия с сайтом удобнее.