3.Методические рекомендации к проведению урока. Вариант 2

Методические рекомендации к проведению урока

Цель обучения: 6.2.2.7 использовать обозначения для записи числовых промежутков;

6.2.2.8 изображать числовые промежутки;

6.2.2.9 находить объединение и пересечение числовых промежутков;

Критерии оценивания:

- изображают числовые промежутки;

- находят объединение и пересечение числовых промежутков;

Организационный момент.

Для актуализации знании учащихся по теме «Числовые неравенства и их свойства» предложите учащимся задания для письменного формативного оценивания. Самостоятельная работа на проверку усвоения цели обучения. На данном этапе у учащихся развивается академическая честность Учащиеся выполняют самостоятельную работу и обмениваются друг с другом для проверки. Ценность: умение работать в сотрудничестве.

1. Вычислить:

а)-12+7-4+9=0

б) (-2)+(-3)+8=3

в)3+6-8+10=11

2. Запишите следующее утверждение в виде неравенства

а) 2,8 является положительным  числом   

б) -10,2 является отрицательным числом

в) х- число положительное

г) n- число отрицательное

д) а- число неположительное

е) b- число неотрицательное

3. Назовите числа, удовлетворяющих неравенству

Решение:

Изучение новой темы: Предлагаю учащимся решить первую задачу – выписать целые решения двойного неравенства. (Вопросы к учащимся: какие числа называются целыми?, какие из них удовлетворяют неравенству?)

Предлагаю учащимся решить вторую задачу. Дать время на запись решения.

Все ли решения неравенства выписаны? Подвести к выводу о том, что:

1) кроме целых решений существуют дробные, 2) их бесконечно много, выписать все не получится.

Как же нам поступить?

(предлагает построить графическую модель (рисунок)).

Но прежде предлагаю вам познакомиться с правилами построения таких моделей.

Размышление, запись вывода:

Все числа выписать не получится!

Могут предложить нарисовать решение на прямой.

Организую фронтальную беседу с одновременным построением моделей и внесением записей на доске и в тетрадях с опорой на слайд.

Обращаю внимание ребят, что мы не только построили графическую модель, но и записали решение неравенств в виде числовых промежутков.

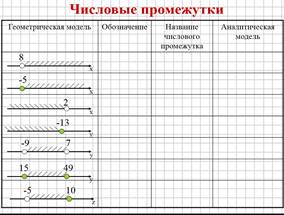
Предложите учащимся объединиться в пары. Раздайте каждой паре таблицу.

В ходе сравнения обсуждают решение, проверяют правильность выполнения задания.

Объедините учащихся в группы. Используйте метод «Карусель» – работа в группах сменного состава.

Предоставьте ресурс. На первом этапе работы, учащиеся разделяют задания в группе между собой. На втором этапе, формируются новые группы учащихся по выбранным заданиям. Объединившись в группы, которые решают одни и те же задания, учащиеся обсуждают, находят решения, осуществляют запись, приходят к полному пониманию решения. На третьем этапе, учащиеся возвращаются в группы исходного состава и объясняют в группе решение своей задачи. Учащиеся проводят самооценивание и взаимооценивание работ по готовым критериям.

Прием «Карусель»

1. Запишите целые числа в промежутке:

а)

2. Запишите и обозначьте данные числовые промежутки:

а) отрезок от 1 до 4
б) интервал от 1 до 4
в) полуинтервал от 1 до 4, включая 4
г) луч от -∞ до 5

3. Запишите промежуток в виде неравенства:

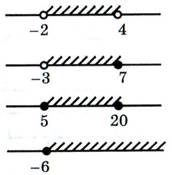
Решение:

1.  

2.  

3.  

Предложите учащимся гимнастику для глаз.

Предложите учащимся вспомнить объединение и пересечение множеств. Обсудите с учащимися пример на объединение и пересечение числовых промежутков.

Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают А∩В. Промежуток [3;5] является пересечением промежутков [-1;5] и [3;7]. Это можно записать так: [-1;5]∩[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих элементов. Если множество не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0;4]∩[6;10]=0.

Объединение числовых промежутков

Каждое число из промежутка [1;7] принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо промежутку [1;5], либо промежутку [3;7], либо им обоим. 

Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают AB.

Промежуток [1;7] является объединением промежутков [1;5] и [3;7]. Это можно записать так: 

Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество не является промежутком. Обратите внимание учащихся на случай объединения и пересечения промежутков, результат которых Ø или R.

Каждой группе предоставляется таблица с записанными на них числовыми промежутками. Учащиеся используют координатную прямую, находят «Пересечение», «Объеденение» промежутков и заполняют таблицу. По окончании обмениваются тетрадями с другими группами и выполняют взаимооценивание.

Самопроверка по образцу.

Задание: Использую координатную прямую, найдите «Пересечение», «Объеденение» промежутков.

1. Найти пересечение и объединение числовых промежутков

2. Найти пересечение и объединение числовых промежутков

3. Найти пересечение и объединение числовых промежутков

 4. Найти пересечение и объединение промежутков

5. Найти пересечение и объединение промежутков

Решение:

 Подведение итогов урока. Рефлексия.

•         Что нового узнали на уроке?

•         – Какую цель мы ставили в начале урока?

•         – Проанализируйте свою работу на уроке.

•         - В чем было затруднение?

Домашнее задание: №995 стр. 227

Ресурсы:

1.Методическое руководство «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.

2.Учебник «Математика 6» А.Е. Абылкасымова, Т.П. Кучер, З.А. Жумагулова.