
Teacher Guides of the Lesson
Theoretical material for the lesson, definitions for concepts
Discussion: How is the ‘electricity’ made?
The demonstrations have shown that ‘making’ electricity involves magnetic fields, but what is really going on? Your students already know that charges moving across a magnetic field experience a force (the BIL force). Now, the metal of a conductor contains mobile charges, the conduction electrons. What happens to these if the conductor is moved across a magnetic field?
Consider a conducting rod PQ moving at a steady speed v perpendicular to a field with a flux density B. An electron (negative charge e) in the rod will experience a force (= Bev) (Fleming's left hand rule) that will push it towards the end Q. The same is true for other electrons in the rod, so the end Q will become negatively charged, leaving P with a positive charge. As a result, an electric field E builds up until the force on electrons in the rod due to this electric field (= Ee) balances the force due to the magnetic field.
Ee = Bev so E =Bv
For a rod of length L, E = V/L and so V/L = Bv
Hence the induced EMF E = BLv
Clearly what we have here is an induced EMF (no complete circuit so no current flows) and already we can see that more rapid movement gives a greater induced EMF.
Now consider what happens when the EMF drives a current in an external circuit. To do this, imagine that the rod moves along a pair of parallel conductors that are connected to an external circuit.
The EMF will now cause a current to flow in the external resistor R. This means that a similar current flows through the rod itself giving a magnetic force, BIL to the left.
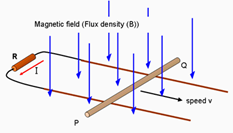
(L is now the separation of the two conductors along which the rod PQ moves.) An equal and opposite force (to the right) is needed to keep PQ moving at a steady speed.
The work done in moving the rod will equal the energy dissipated in the resistor.
In a time t, the rod moves a distance d = v t
Work done on the rod = BIL v t
Energy dissipated in R = power x time = EMF I t
giving BIL v t = EMF I t
or, as before, EMF = BvL
But in this case it can be seen that the electrical circuit encloses more magnetic field as the rod is moved along and that in one second, the extra area enclosed will be v l.
i.e. induced EMF E = B ´ area swept out per second = B ´ A / t
We have already called B the flux density, so it is perhaps not surprising that the quantity B ´ A can be called the magnetic flux, F.
Thus induced EMF = F / t = rate of change of flux
And more generally E = dF / dt
How can the induced EMF be increased? Discussionshouldleadto:
But there is a further possibility and this is to increase the number of turns of wire N in our circuit. By doing this, the flux has not been altered but the flux linkage (N F) will have increased. Hence it is more correct to say that
induced EMF = rate of change of flux linkage
E = N ´ dF/dt
This relationship is known as Faraday's law: - when the flux linked with a circuit changes, the induced EMF is proportional to the rate of change of flux linkage.
Finally, remind your students that the magnetic force on our simple generator (a) (b) was in a direction which would make the bar slow down unless an external force acted. This is an example of Lenz's law: - the direction of the induced EMF is such that it tends to oppose the motion or change causing it.
To include this idea in our formula, a minus sign has to be introduced, giving;
E = – N ´ dF/dt
Earlier in this chapter, we saw that electromagnetic induction occurs whenever a conductor cuts across lines of magnetic flux – for example, when a coil is rotated in a magnetic field so that the magnetic flux linking the coil changes. We can use Faraday’s law of electromagnetic induction to determine the magnitude of the induced e.m.f. in a circuit:
The magnitude of the induced e.m.f. is proportional to the rate of change of magnetic flux linkage.
We can write this mathematically as:
E ∝Δ(NΦ)/Δt
![]()
where Δ(NΦ) is the change in the flux linkage in a time Δt. It allows us to calculate the magnitude of theinduced e.m.f.,its direction is given by Lenz's law.
Instructions for demonstrations and safety
Warning: experiments should be performed under the supervision of teachers or students follow the instructions of safety procedures.
Additional guidelines for organizing a lesson
1. Organization moment. Establishing emotional state. Checking for absent students.
2. Teacher introduces the topic and objectives of the lesson, assess criteria.
3. Teacher provides a class discussion for: How is the ‘electricity’ made? Individual students were called on to respond to questions and share their own opinions/thoughts. The previous demonstrations showed that ‘making’ electricity involves magnetic fields, but what is really going on?
4. Teacher may help students to derive the equation of electromagnetic induction.
5. Teacher asks learners to answer the Questions on use of the Faraday law of electromagnetic induction individually.
6. Pairs check and assess each other’s work and provide fair and helpful feedback by using an answer sheet.
7. At the end of the lesson students are encouraged to reflect on what they have learned and what they need to improve.
Recommendations for formative assessment
Activity1. Students discuss learning objectives and assess criteria.
Activity2. A class discussion about: How is the ‘electricity’ made? Individual students are
called on to respond to questions and share their own opinions/thoughts. The previous
demonstrations showed that ‘making’ electricity involves magnetic fields, but what is
really going on?
Activity3. Students to derive the equation of electromagnetic induction by a teacher support.
Activity4. Learners answer the Questions on use of the Faraday law of
electromagnetic induction individually.
Activity5. Pairs check and assess each other’s work and provide fair and helpful feedback by
using an answer sheet.
Activity6. At the end of the lesson students are encouraged to reflect on what they have learned
and what they need to improve.
Answers, criteria for assignments, additional materials for the lesson
1. For the following scenarios, determine whether the magnetic flux changes or stays the same. If the flux changes: indicate whether it is increasing or decreasing (and in which direction). Explain your answer.
Ans.
![]()
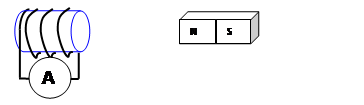 a.
The magnet is held stationary to the solenoid.
a.
The magnet is held stationary to the solenoid.
Ans.
![]() increasing
increasing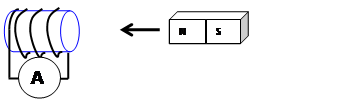 b.
The magnet is moving toward the solenoid.
b.
The magnet is moving toward the solenoid.
Ans. 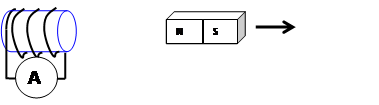
c. The magnet is moving away from the
solenoid.
![]() decreasing
decreasing
2. Find the direction of the induced current for the solenoid in the figure below, when the magnet is _____.
Ans. i=0
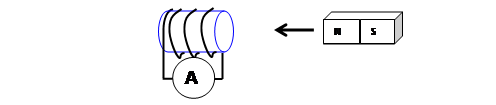
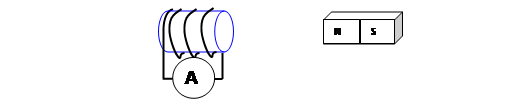
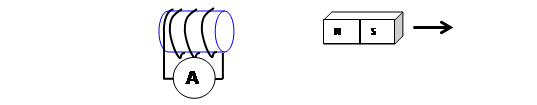 a.
stationary to the solenoid.
a.
stationary to the solenoid.
Ans. counter-clockwise
b. moving toward the solenoid.
Ans. clockwise
c. moving away from the solenoid.
List of useful links and literature
Douglas C. Giancoli, Physics Principles with Applications, Seventh edition 2014.
Keith Johnson Physics for You IGCSE Updated Edition 2011
https://tap.iop.org/fields/electromagnetism/414/page_46948.html
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.