Методические рекомендации к данному уроку

  Начните урок с организационного момента, приветствие, отметка отсутствующих, проверка готовности учащихся к урок. Совместно с учащимися определите цели урока, критерии оценивании, обсудите ход урока. Проведите  выборочную проверку домашнего задания.

Теоретический материал: При решении задач математик Леонард Эйлер использовал идею изображения множеств с помощью кругов, поэтому они получили название «круги Эйлера». Впервые он использовал их в письмах к немецкой принцессе. Эйлер писал, что «круги очень подходят для того, чтобы облегчить наши размышления».

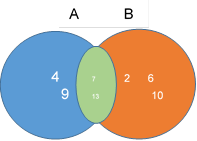Пересечение множеств А и В называется множество, состоящее из элементов, которые принадлежат и множеству А, и множеству В.

 Его обозначают так: АВ или АВ=С.

Например, А=; В=  

Если множество А и В не имеют

общих элементов, то их пересечением

является пустое множество АВ=.

Если А , то АВ=В  и А  В=A,где А и В любое множество

Объединением множеств А и В называется новое множество, состоящее из тех элементов, которые входят хотя бы в одно из множеств А или В.

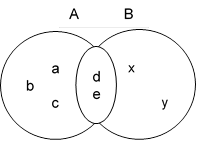Обозначают: АВ или АВ=D

Например, N=;P= ;

NP= 

Основные свойства операций над свойствами. Операции объединения и пересечения над множествами обладают рядом свойств. Мы рассмотрим основные, наиболее важные свойства этих операций.

AÈ(BÈC)=(AÈB)ÈC -ассоциативность объединения;

AÇ(BÇC)=(AÇB)ÇC -ассоциативность пересечения;

AÈB=BÈA-коммутативность объединения ;

AÇB=BÇA- коммутативность пересечения

        Проведите устное формативное оценивание. Предложите учащимся ответить на вопросы по пройденной теме:

1.Что означает слово «множество»?

-          Множество – это набор или совокупность предметов одинаковой природы.

2.Какие названия применяются для обозначения множеств?

-          Стадо, табун, коллектив, семья, оркестр, библиотека.

3.Как различаются множества по числу элементов?

-          Множества бывают конечные, бесконечные и пустое множество.

4.Какими способами можно задать множество?

-          Множество можно задать перечислением или с помощью характеристического свойства.

5.Какое свойство называется характеристическим свойством?

-          Характеристическим свойством называется такое свойство, которым обладают все элементы данного множества и не обладают никакие другие объекты.

6. Что называется пересечением множеств А и В?

Пересечением множеств А и В называется множество, в которое входят те и только те элементы, которые содержатся в А и В одновременно.

7.Что называется объединением множеств А и В?

Объединением множеств А и В называется множество, состоящее из тех элементов, которые входят хотя бы в одно из множеств А или В.

8. В данном множестве все элементы, кроме одного, обладают некоторыми свойствами. 

Опишите его и найдите лишний элемент.

       Предложите учащимся объединиться в пары и выполнить задания с последующей взаимопроверкой.

1 задание

Запишите перечислением элементов множество цифр А числа 3856 и множество цифр С 54267.

а)  запишите перечислением элементов пересечение множеств А и С и обозначьте его;

b) запишите перечислением элементов объединение множеств А и С и обозначьте его;

c) отобразить на диаграмме эйлера-венна

Ответ:

а) A  

b) A  

c)

2 задание

В классе 16 мальчиков. Из них 14 мальчиков в свободное время увлекаются футболом, 9 мальчиков увлекаются шахматами. Сколько мальчиков в классе в свободное время увлекаются и футболом, и шахматами, если все мальчики класса занимаются этими играми?

Ответ:

14+9 =23

23 -16 =7

Ответ: 7 мальчиков

3 задание

Множество С содержит 5 элементов, множество D - 7 элементов. Если пересечение этих множеств содержит 3 элемента, то сколько элементов содержит их объединение?

1)7+5=12
2)12-3=9
Ответ 9 элементов

Дескрипторы:

·         знает определения пересечения и объединения множеств;

·         может найти пересечение и объединение множеств;

·         может записывать результаты, используя символы È, Ç;

·         решает задачи, используя диаграммы Эйлера-Венна.

Оценим работу по мере выполнения, за правильное решение можно выдавать фишки.

        Предложите учащимся задания для групповой работы, примените при этом прием «Посол». Разместим группы по 3-4 человека в классе.

Когда группа выполнила задание, один ученик из каждой группы выбирается «представителем» и перемещается к другой группе, чтобы объяснить и обобщить, и выяснить идеи другой группы.  Затем представитель возвращается в свою группу, чтобы сообщить, что он узнал. Это эффективный метод избегания скучного и повторяющегося «сообщения своей группе». Это также способствует использованию языка представителя и создает группу активных слушателей.

Задача 1. В классе учатся 40 человек. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по истории – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4 человека, по истории – 11 человек. Семь учеников имеют «тройки» и по математике и по истории, а 5 учеников – «тройки» по всем предметам. Сколько человек учится без «троек»? Сколько человек имеют «тройки» по двум из трех предметов?

Решение. Нарисуем круги Эйлера. Внутри большего круга, изображающего всех учеников класса, поместим три меньших круга М, Р, И, означающих соответственно математика, русский язык и история. Так как число ребят, имеющих «тройки» по математике и истории, равно 7, то число учеников, имеющих только две «тройки» - по математике и по истории, равно 7-5=2. Тогда 17-4-5-2=6 учеников имеют две «тройки» - по математике и по русскому языку, а 22-5-2-11=4 ученика только две «тройки» - по истории и по русскому языку. В этом случае без «тройки» учится 40-22-4-6-4=4 ученика. А имеют «тройки» по двум предметам из трех 6+2+4=12 человек.

Задача 2. В 5 классе нашей школы 22, в 6 классе – 16, в 7 классе – 23 ребят. Известно, что кружки по лыжам, шахматам и спортивным играм ходят 4 человека. Каждые 2 секции посещают 9 человек. Сколько человек ходит из каждого класса на секции? Сколько учеников не ходит ни на какой спортивный кружок?

Решение: Если на все три кружка ходят 4 ученика, а на каждые два – 9 человек, то две секции с 5 и 6 класса, с 6 и 7 класса, с 5 и 7 класса посещают по 5 человек. Получаем 5+5+4=14 пятиклассников посещают кружки, 22-14=8 человек не ходят ни на какой кружков. Рассуждая также, из шестиклассников 16-14=2 ученика никуда не ходя, а из семиклассников – 23-14=9 человек.

Ответ: 14 учеников с каждого класса посещают кружки, не ходят ни на какой из 5-ого – 7, из 6-ого – 2, из 7-ого – 9 учеников.

Задача 3. В классе 32 человека. Из них 14 играют в баскетбол, 24 - в пионербол, 16 - в волейбол. Увлекаются двумя видами спорта - баскетболом и пионерболом - шестеро, баскетболом и волейбол - четверо, пионерболом и волейболом - четверо. Трое ни чем не занимаются. Сколько ребят увлекается всеми видами игры?

Решение. Воспользуемся кругами Эйлера.

1)32-3=29 (ч.) – играют хотя бы в одну игру.

2)14-6-4-x = 4-x (ч.) – играют только в баскетбол.

3)24-6-4-x = 14-x (ч.) – играют только в пионербол.

4)16-4-4-x = 8-x (ч.) – играют только в волейбол.

5)4-x+14-x+8-x+5+6+4 =29 (ч.)

41-3x=29

x = 4 (ч.)

Ответ: четыре человека увлекаются всеми тремя видами спорта.

Группы, решив каждое из заданий, обмениваются и проверяют друг друга (взаимооценивание). Учащиеся сверяют свои ответы и определяют правильно ли они оценили друг друга. Выставляют себе баллы.

Дескрипторы:

·         знает определения пересечения и объединения множеств;

·         может найти пересечение и объединение множеств;

·         может записывать результаты, используя символы È, Ç;

·         решает задачи, используя диаграммы Эйлера-Венна.

        Для организации работы по актуализации опорных знаний предложите учащимся индивидуальные задания по уровням. Учащиеся составляют и проговаривают план действий с помощью учителя. Выполняют задания на доске и в тетрадях.

Уровень А.

Задача 1. Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро - собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг?

Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом - собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части "кошачьего" круга ставим цифру 4 (6 - 2 = 4). В свободной части "собачьего" круга ставим цифру 3 (5 - 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

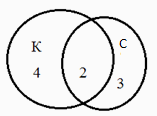
Ответ. 9 подруг.

Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 - в районной. Сколько учеников не являются читателями школьной библиотеки?

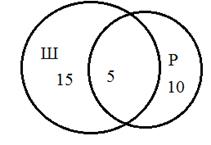
Решение: Пусть круг Ш изображает читателей только школьной библиотеки, круг Р - только районной. Тогда ШР - изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно:

(не Ш) = Р - ШР. Всего 30 учеников, Ш = 20 человек, Р = 15 человек. Тогда значение ШР может быть найдено так (см. рисунок): ШР = (Ш + Р) - 30 = (20 + 15) - 30 = = 5, т.е. 5 учеников являются читателями школьной и районной библиотек одновременно. Тогда (не Ш) = = Р - ШР= 15 - 5= 10.

Ответ: 10 учеников не являются читателями школьной библиотеки.

Уровень В. Задача 3. Любимые мультфильмы. Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: "Белоснежка и семь гномов", "Винни Пух", "Микки Маус". Всего в классе 28 человек. "Белоснежку и семь гномов" выбрали 16 учеников, среди которых трое назвали еще "Микки Маус", шестеро - "Винни Пух", а один написал все три мультфильма. Мультфильм "Микки Маус" назвали 9 ребят, среди которых пятеро выбрали по два мультфильма. Сколько человек выбрали мультфильм "Винни Пух"?

Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только "Белоснежку" выбрали 16-6-3-1=6 человек. Только "Микки-Маус" выбрали 9-3-2-1=3 человека.

Только "Винни-Пух" выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что "Винни-Пух" выбрали 7+6+1+2=16 человек.

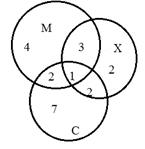
Задача 4. Хобби. Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу - 8 человек, спортивную школу - 12 человек, музыкальную и художественную школу- 3, художественную и спортивную школу - 2, музыкальную и спортивную школу - 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?

Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только музыкальную школу посещают 10-3-2-1=4 учащихся. Только художественную школу посещают 8-3-2-1=2 учащихся. Только спортивную школу посещают 12-2-2-1=7 учащихся.

Только одну школу посещают 4+2+7=13 учеников.

Ни в чем себя не развивают 24-(4+2+7+3+2+2+1)=3 учащихся.

Ответ. 13 учеников посещают только одну школу, 3 учащихся себя не развивают.

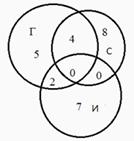
Уровень С. Задача 5. О головоломках. На полке стояло 26 различных математических игр - головоломок. В 4 из них поиграл и Гриша, и Саша. Игорь попробовал проиграть 7 игр, которых не касались ни Гриша, ни Саша, и две головоломки, в которые играл Гриша. Всего Гриша играл в 11 математических игр - головоломок. Во сколько головоломок сыграл Саша?

Решение: Так как Гриша всего проиграл в 11 игр, из них 4 головоломки решены Сашей и 2 головоломки - Игорем, то 11 - 4 - 2 = 5 - игр проиграно только Гришей. Следовательно, 26 - 7 - 2 - 5 - 4 = 8 - головоломок решено только Сашей. А всего Саша играл в игр.

Ответ. 12 игр решил Саша.

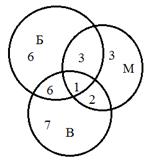
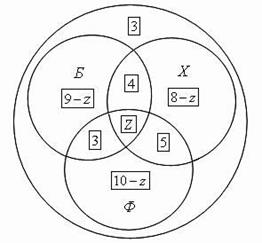
Задача 7. Спорт для всех. В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом. Сколько ребят увлекаются одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?

Решение. Воспользуемся кругами Эйлера.

Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта - баскетболом занимаются 16 - (4 + z + 3) = 9 - z; одним лишь хоккеем 17 - (4 + z + 5) = 8 - z; одним лишь футболом

18 - (3 + z + 5) = 10 - z. Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам: 3 + (9 - z) + (8 - z) + (10 - z) + 4 + 3 + 5 + z = 38,z = 2. Таким образом, двое ребят увлекаются всеми тремя видами спорта. Складывая числа 9 - z, 8 - z и 10 - z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек.

Ответ: Двое ребят увлекаются всеми тремя видами спорта человека. Увлекающихся лишь одним видом спорта: 21 человек.

Дескрипторы:

·         знает определения пересечения и объединения множеств;

·         может найти пересечение и объединение множеств;

·         может записывать результаты, используя символы È, Ç;

·         решает задачи, используя диаграммы Эйлера-Венна.

В конце урока учащиеся проводят рефлексию:

- что узнал, чему научился

- что осталось непонятным

- над чем необходимо работать

Домашнее задание:

№1 Кирпич весит 1 кг и еще половину веса кирпича. Сколько весит кирпич?

Решение

Пусть x - вес кирпича. Тогда:
x = 0,5x + 1 или
x = 1/0,5

Ответ: 2 кг.

С учебника № 10-13, стр 75

Ресурсы:

1.      http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/635933/

2.      http://www.reshim.su/blog/krugi_ehjlera/2016-07-04-681

3.      https://www.youtube.com/watch?v=YQzfRj9wiWM

4.      http://festival.1september.ru/articles/635933/

5.      Математика 5 класс. Мектеп, 2017 год

https://rnpc.almatykitap.kz/?id=154&#

Скачано с www.znanio.ru