4. Методические рекомендации к проведению урока. Вариант 2.

Методические рекомендации к проведению урока

Тема: Координатная плоскость. Прямоугольная система координат

Цели обучения:

·        6.3.1.1 усвоить понятие координатной плоскости;

·       6.3.1.2 строить прямоугольную систему координат;

·        6.3.1.3 понимать, что упорядоченная пара чисел (х; у) задает точку в прямоугольной  системе координат и каждой точке соответствует единственная упорядоченная пара чисел, называемые координатами точки;

·        6.3.1.4 строить точку в системе координат по ее координатам и находить координаты точки, заданной на координатной плоскости.

Организационный момент.

Проверка готовности учащихся к уроку. Обеспечить в ходе урока усвоение нового материала: понятие координатной плоскости, координат точки на плоскости, абсциссы и ординаты точки; умение выполнять упражнения, предполагающие нахождение координат точки на координатной плоскости и построение точки по ее координатам; обеспечить условия для развития математической речи учащихся, внимания, памяти, логического мышления, воображения; содействовать осознанию практической значимости изучаемого материала.

Проверка домашнего задания.

Учащиеся по готовому решению проверяют свою домашнюю работу (самооценивание).

Для введения в новую тему задание 1. Учащиеся индивидуально выполняют задание 1:

Франция подарила миру много выдающихся людей в области науки и культуры. Узнайте фамилии двух знаменитых французов. Для этого найдите на прямой точки с указанными координатами, а из букв получите фамилии. Используя полученные фамилии, заполните пропуски в тексте, учитывая падежные окончания.

Немного истории.

Кратко расскажите об ученом.

Рене Декарт – выдающийся французский философ, математик, биолог и физик.

Одним из наиболее известных его достижений в математике является изобретение координатной прямой и плоскости. В 1637 году ученым была написана самая известная его работа «Рассуждение о методе».

Среди открытий, сделанных эти ученым, - закон преломления света, поясняющий образование радуги. В физиологии он ввел понятие рефлекс.

Постановка темы урока, целей обучения и критериев оценивания.

Объяснение новой темы. Учитель с помощью презентации или видео объясняет новую тему. План изучения материала/вопросы/пункты:

1.     Где используются координаты в жизни (география, многие способы указания места: шахматы, морской бой, место на концерте и т.д.).

2.     Прямоугольная система координат на плоскости.

3.     Координатный четверти

4.     Координаты точки.

5.     Построение точки.

6.   Алгоритм построения точки

7.   Алгоритм отыскания координат точки

Закрепление материала. Учащиеся индивидуально выполняют задания 2-7.

Задание 2.

А уровень

Запишите координаты отмеченных точек:

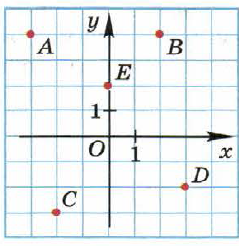
Задание 3.

В уровень

Отметьте на координатной плоскости точки.

Задание 4.

В уровень

Отметьте на координатной плоскости точки.

Задание 5.

В уровень

Отметьте на координатной плоскости точки.

Задание 6.

С уровень

Для каждой четверти укажите, какие знаки имеют координаты точек, находящихся в этой четверти:

Задание 7.

С уровень

Установите соответствие между точками, заданными своими координатами, и координатными четвертями, в которых они расположены.

Физкультминутка.

Учитель просит учащихся выполнить упражнения.

Быстро встали, улыбнулись.

Выше, выше потянулись.

Ну-ка плечи распрямите,

Поднимите, опустите.

Вправо, влево повернитесь,

Рук коленями коснитесь.

Сели, встали, сели, встали.

И на месте побежали.

Работа в группах. Учащиеся в группах выполняют задание.

Задание 8.

Нарисуйте собаку по заданным на координатной плоскости точкам:

Домашняя работа.

Задание 9.

Отметьте точки на координатной плоскости:

Проведение рефлексии, согласно ожидаемых результатов, поставленных в начале урока и критериев оценивания.

Подведение итогов урока.

Учащиеся делают вывод по уроку отвечая на вопросы:

•      Сколько чисел надо указать, чтобы задать положение точки на координатной плоскости?

•      Как называют второе из чисел, задающих положение точки на координатной плоскости?

Рефлексия.

«Неоконченное предложение»

Сегодня на уроке я узнал … .

Я научился … .

Мне понравилось … .

Учащиеся с хорошими учебными способностями во время работы самостоятельно помогают одноклассникам при выполнении дифференцированных заданий. Во время выполнения заданий учащиеся могут обращаться к ним за консультацией. Учитель оказывает индивидуальную помощь учащимся, затрудняющимся в решении самостоятельной работы.

Формативное оценивание осуществляется во время работы учащихся в группах и выполнении индивидуальных заданий.

Формативное оценивание осуществляется во время работы учащихся в группах и выполнении индивидуальных заданий.

Список полезных ссылок и литературы

1.     http://www.e-osnova.ru/PDF/osnova_3_40_7869.pdf

2.     http://shkolo.ru/pryamougolnaya-sistema-koordinat/

3.     https://bilimland.kz/ru/subject/matematika/6-klass

4.     http://www.myshared.ru/slide/622591/

5.     http://www.myshared.ru/slide/351362/

6.     Математика: 6 класс: учебник для учащихся общеобразовательных организаций/А.Г.Мерзляк, В.Б.Полонский, М.С. Якир. - М.:ВентанаГраф,2014.-304 с.:ил.

7.     Математика 6 класс. Тетрадь 2. Задания для обучения и развития учащихся. / Беленкова Е.Ю., Лебединцева Е.А.- М.; Интеллект-Центр, 2013. – 176

8.     Математика. 6 кл.: учеб.для общеобразоват.учреждений: в 2 –х частях. Ч.1/С.А.Козлова, А.Г.Рубин. – 2-е изд. – М.:Баласс, 2013. – 208 с., ил. (Образовательная система «Школа 2100»).

9.     Контрольные и самостоятельные работы по математике: 6 класс: к учебнику Н.Я.Виленкина и др. «Математика. 6 класс»/М.А. Попов. – 5-е изд., перераб. – М.: Издательство «Экзамен», 2009. – 95, (1) с.

10. Математика. Арифметика. Геометрия. Тетрадь-тренажер. 6 класс: пособие для учащихся общеобразовательных организаций/Е.А.Бунимович, Л.В.Кузнецова, С.С.Минаева и др. – 3-е изд., – М.: Просвещение, 2013. – 160 с.

11. Скачано с www.znanio.ru