4. Методические рекомендации к проведению уроку. Вариант 2

Методические рекомендации к проведению урока

Цели обучения:

 6.1.2.17 применять свойства сложения и умножения рациональных чисел.

Критерии оценивания:

- использовать свойства сложения и умножения рациональных чисел для устного счета, упрощении выражений, нахождения числовых значений выражений.

Организационный момент. Мотивация к учебной деятельности. Беседа.

     Урок начните с концентрации внимания учащихся. Как для данного урока, так и для последующих уроков важно умение учащихся применять свойства сложения и умножения рациональных чисел.

Для повторения пройденного материал предложите учащимся Интеллектуальную разминку.

Сравните с нулём:

( -1-2-3-4-5-6-7)·(-157)                    и  0

(1+2+3+4+5+……99) · (300-1)       и   0

(-1) · (-2) · (-3) · …. · (-10)                и 0

(-2) ·  (-4) · (-6) · …. · (-102)             и 0

Проведите устное формативное оценивание.

Актуализация знаний.

На доске таблица с заданиями, где есть ошибки. Необходимо проверить результат, и поставить «+», если результат правильный, и «-», если не правильный.

- 0,6 · 4 = - 2,4                               Дорогу

- 6 · (-0,3) = 0,18                           Математика

- 1,5 · 2 = - 3                                  Осилит

- 3 · (- 0,6) = - 1,8                          Гимнастика

- 1 + 7    =   4                                  Ума

     2

 -5 + 9   =  1                                   Идущий

      4

Учащиеся делятся на группы следующим образом.

Необходимо подряд прочитать слова, напротив которых поставили «+». Должно получится высказывание.   «Дорогу осилит идущий», теперь слова, напротив которых «-»

«Математика гимнастика ума».

Изучение новой темы: Предложите учащимся провести мини-исследование:

Найдите значение произведения:

1.      (-0,2)·7·(-5)

2.      (-1,5)·(-0,25)·2·(-4)

Способ 1: Последовательно умножая числа

Способ 2: Группируя множители таким образом, чтобы их произведения были целыми числами.

- изменилось ли значение произведения? Каким способом удобнее?

Предложите учащимся рассмотреть свойства умножения. Свойства умножения неотрицательных чисел также справедливы и для любых рациональных чисел. Умножение, как и сложение, обладает переместительным и сочетательным свойствами

Переместительное и сочетательное свойства умножения позволяют переставлять и группировать множители, что дает возможность упрощать выражения.

Задание

Найдите произведение.

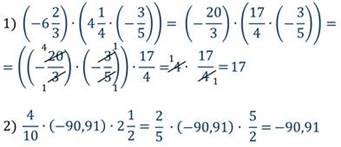
Умножение рациональных чисел обладает и распределительным свойством умножения относительно сложения.

Для любых рациональных чисел а, b и с верно равенство:

Для того чтобы умножить сумму на число можно сначала умножить первое слагаемое на это число, потом второе слагаемое на это число, а затем полученные результаты сложить.

Пример

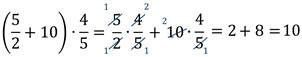
Распределительное свойство умножения справедливо и в обратную сторону.

Такое преобразование выражения называют вынесением общего множителя за скобки.

Пример

Учащиеся записывают все, что узнали по данной теме.

Групповая работа. Решение практических задач по вариантам.

Кроме понимания содержания понятия умножение рациональных чисел учащиеся должны научиться применять свойства сложения и умножения рациональных чисел;

Для закрепления и оценки уровня умения применять свойства сложения и умножения рациональных чисел;

Вариант 1. Найдите значение выражения, применив распределительное свойство:

Вариант 2.                                              

Найдите значение выражения, применив распределительное свойство:

В а р и а н т 3.                                            

Найдите значение выражения, применив распределительное свойство:

23

В а р и а н т 4.                                      

Найдите значение выражения, применив распределительное свойство:

-38.3

Дескрипторы:

Определяет свойство для рационального способа решения;

Выполняет сложение или умножение для положительных чисел;

 Выполняет сложение или умножение для отрицательных чисел;

Выполняет сложение или умножение для чисел с разными знаками.

Групповая работа.

Предложите учащимся проверочную работу. Учащиеся работают в группах. Задание у всех групп одинаковое, но совместная работа с одноклассниками одного уровня позволит раскрыться каждому ученику.

 Проверочная работа направлена на оценивание знаний, умений и навыков учащихся по использованию свойств сложения и умножения рациональных чисел для устного счета, упрощениия выражений, нахождения числовых значений выражений. Группы обмениваются решениями, проводят самооценивание  и взаимооценивание.

Задания для групп:

        1. Найдите произведение: 

 а) ;          

б) ;        

 в)         

      2. Выполните действия: .

      3. Фермерское хозяйство собрало 960т зерна. 75% собранного зерна составила пшеница, а  остатка рожь. Сколько тонн ржи собрало фермерское хозяйство? 

        Ответ: 200 тонн

      4. В один пакет насыпали кг сахара, а в другой – в 4 раза больше. Насколько больше сахара насыпали во второй пакет, чем в первый?      

   Ответ: 4,2 кг

      5. Не приводя к общему знаменателю, сравните дроби   и .

Дескрипторы:

Определяет свойство для рационального способа решения;

Выполняет сложение или умножение для положительных чисел;

 Выполняет сложение или умножение для отрицательных чисел;

Выполняет сложение или умножение для чисел с разными знаками.

Дифференциация выражена в виде заданий, требующих разного уровня математической подготовленности, а так же с учетом скорости мышления и возрастных особенностей учащихся.

Подведение итогов урока. Рефлексия.

Рефлексия. Учащиеся дополняют следующие предложение:

Сегодня на уроке я научился…

Сегодня на уроке мне понравилось…

Сегодня на уроке я повторил…

Сегодня на уроке я закрепил…

Сегодня на уроке я поставил себе оценку

Домашнее задание: №529 стр.123

Ресурсы:

1.       Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

2.       Алдамуратова Математика. 6 класс. Алматы. «Атамура». 2011 год.

      3 . http://www.for6cl.uznateshe.ru/sochetatelnoe-svojstvo-umnozheniya/