Методические рекомендации к уроку

Тема урока "Числовые промежутки. Объединение и пересечение числовых промежутков"

Цели обучения:

6.2.2.7

использовать обозначения для записи числовых промежутков;

6.2.2.8

изображать числовые промежутки;

6.2.2.9

находить объединение и пересечение числовых промежутков;

Критерии оценивания

Учащиеся

 знают:

□     как правильно читать неравенства;

□     как записывать, используя математическую символику, неравенства;

□     как находить объединение и пересечение числовых промежутков.

умеют

□     -изображать числовые промежутки;

□     использовать обозначения для записи числовых промежутков.

□     находить объединение и пересечение числовых промежутков.

Теоретический материал

Определение: Множество чисел, расположенных между числами  и , называют числовым промежутком.

1. Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают АÇВ.
2. Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают АÈВ.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Решить задания на повторение.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить учащимся задания подобные заданиям Приложения 1. Каждый выполняет самостоятельно.

Приложение 1

1.Как называется  промежуток: (3;7)

А) отрезок  Б) интервал  в) луч     г) полуинтервал

2. Как называется  промежуток: [2;7]

А) отрезок   Б) интервал    в) луч     г) полуинтервал

3. Как называется  промежуток: (-14;-7]

А) отрезок   Б) интервал    в) луч  г) полуинтервал

4. Как называется  промежуток: [10;19)

А) отрезок  Б) интервал  в) луч     г) полуинтервал

5. Как называется  промежуток: (-1;17)

А) отрезок  Б) интервал  в ) луч     г) полуинтервал

6. Как называется  промежуток: (-∞;7)

А) отрезок  Б) интервал  в) луч     г) открытый луч

7. Как называется  промежуток: (3;+ ∞)

А) отрезок  Б) интервал  в) луч     г) открытый луч

8. Как называется  промежуток: (-∞;-2]

А) отрезок  Б) интервал  в) луч     г) открытый луч

9 Как называется  промежуток: (-4;9]

А) полуинтервал  Б) интервал  в) луч     г) открытый луч

10.Как называется  промежуток: (-∞;10)

А) отрезок  Б) интервал  в) луч     г) открытый луч

После окончания выполнения, попросить обменяться тетрадями с соседом. Взаимопроверка по ключу. Собрать информацию о выполнении. Разобрать один из вариантов.

Работа с классом. Ввод новой темы.

Пересечение числовых промежутков

Множество, составляющее общую часть некоторых множеств А и В, называют пересечениемэтих множеств и обозначают АÇВ. Промежуток [3;5] является пересечением промежутков [1;5] и [3;7]. Это можно записать так: [1;5]Ç[3;7]=[3;5].

Промежутки [0;4] и [6;10] не имеют общих элементов. Если множество не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков

[0;4]Ç[6;10]=Æ.

Первичное закрепление. Для отработки навыков умения работать c пересечением  множеств выполнить упражнения по учебному пособию аналогичные данным.

Используя координатную прямую, найдите пересечение промежутков:

а) (1;8) и (5;10);

б) [-4;8] и [-6;6];

в) (-5;1] и (-4;2];

г) (-¥;3] и [0;+¥].

Ответ: а) (5;8); б) [-4;6]; в) (-4;1]; г) [0;3].

3. Объединение числовых промежутков

Каждое число из промежутка [1;7] принадлежит хотя бы одному из промежутков [1;5] и [3;7], то есть, либо промежутку [1;5], либо промежутку [3;7], либо им обоим.

Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают АÈВ.

Промежуток [1;7] является объединением промежутков [1;5] и [3;7]. Это можно записать так: [1;5][3;7]=[1;7].

Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество [0;4]È[6;10] не является промежутком.

 [ -4;3)  (0;+∞) = ( 0;3)

[ -4;3)  (0;+∞) = [ - 4; + ∞)

Дальнейшее закрепление провести в группах.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 2

1) Определите, какие из неравенств являются строгими, а какие не строгими:

х ≥- 5;             х< -4;              2 ≤ х 0≤ 8;      х ≤ 3;               х > -1;             4 ≤ х<  0;

х > 7;              х ≤ -2;             -4 < х ≤ 0.

(Какие неравенства остались? Как они называются?)

2) Изобразите на координатной прямой множество чисел, удовлетворяющих неравенствам.

3) Запишите числовые промежутки соответствующие решениям неравенств.

4) Изобразите заданные промежутки на координатной прямой. Найдите пересечение и объединение промежутков.

[ -4;3) и (0;+∞)

5) Изобразите заданные промежутки на координатной прямой. Найдите пересечение и объединение промежутков. Запишите:

а) (1;7) и (4; 9]
б) [ -5; 5) и[ -3;7]
в) [ -5;0) и (-2;4]

Ответы:

а) (1;7)  (4; 9] = (1; 4);        (1;7)  (4; 9] = (1; 9]
б) [ -5; 5) [ -3;7]= [-3;5)     [ -5; 5) [ -3;7]= [-5;7]

в) [ -5;0)  (-2;4] = (-2;0)      [ -5;0)  (-2;4] = [-5;4]

Дополнительное задание:

Найдите пересечение и объединение множеств A=(−∞, −15)∪{−5}∪[0, 7]∪{12} и

B=(−20, −10)∪{−5}∪(2, 3)∪{17}.

Решение.

Изобразить данные числовые множества на координатных прямых, это позволит нам получить изображения их пересечения и объединения:

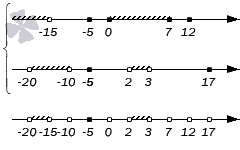
Ответ:

A∩B=(−20, −15)∪{−5}∪(2, 3) и A∪B=(−∞, −10)∪{−5}∪[0, 7]∪{12, 17}.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям.

Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.      "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.      "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.      Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.      Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.      Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.      http://www.yaklass.ru

2.      https://school-assistant.ru