4. Повтор Процент. Методические указания к уроку. Вариант 2

Методические указания к уроку

тема "Повторение курса математики 5 класса. Процент."

Цели обучения:

5.1.2.34 находить процент данного числа; 5.1.2.36 находить число по данному проценту; 5.5.1.6 решать текстовые задачи на проценты;

 Критерии оценивания:

Учащийся:

·         умеет переводить дроби в проценты и проценты в дроби;

·         умеет находить процент от числа;

·         умеет находить число по его проценту;

·         умеет решать текстовые задачи на проценты.

Из истории:

Дать краткую историческую справку.

Первые таблицы процентов были составлены ещё вавилонянами. Индийцам проценты были известны еще в V в. Проценты были особенно распространены в Древнем Риме. В Европе десятичные дроби появились на 1000 лет позже, их ввел бельгийский учёный Симон Стевин. В 1584г. он впервые опубликовал таблицу процентов.

Поставив вопрос: Знаешь ли ты? в ходе диалога выяснить какой еще информацией владеют учащиеся. Если уровень информации о проценте не удовлетворил класс, то дайте желающим подготовить реферат по этой теме.

Теоретический материал.

Процент - части целых чисел в одних и тех же сотых долях, т.е. сотая часть любой величины: пути, массы, площади, количества объёма…. Сотую долю целого (принимаемого за единицу) принимают за 1 процент. Обозначают знаком - .

Что понимают под словом "процент"

Один тиын - один процент от одного тенге,

один сантиметр - один процент от одного метра,

один ар - один процент гектара,

две сотых - один процент от числа два.

Это интересно:

На латыни  будет звучать «17 per cent – 17 на сотню» или по-русски «17 про­центов». Нужны ли проценты? В математике не нужны, т.к. есть десятичные дроби. Проценты - это договоренность, чтобы лучше понимать друг друга, в таких науках как экономика, бухгалтерия и другие.

Ход урока

Организационный момент. Мотивация к учебной деятельности.

Тема «проценты» одна из важных тем курса математики. Необходимо учащимся объяснить: хотя в математике использование дробей решает те же задачи, но в практике часто удобнее использовать проценты. Вопросы, связанные с процентами, показывают учащимся, что приобретаемые ими математические знания применяются в повседневной жизни. Интерес к теме поддерживается также и содержанием задач. Содержания задач должны быть приближены к современной тематике и к жизненному опыту учащихся. Это служит достаточно сильным мотивом для решения предлагаемых задач.

Воспоминание о процентах как о математической величине, опирается на предметно практическую деятельность школьников, на геометрическую наглядность и геометрическое моделирование. Учащиеся должны выполнять задания, в которых требуется заштриховать, закрасить, начертить или вырезать часть фигуры. Используйте рисунки и чертежи, помогающие разобраться в задаче и увидеть пути ее решения.

Выясните сотые доли некоторых, часто используемых величин, установите соответствия (Приложение 1):

1) Сколько килограммов в одном центнере? Какую часть центнера составляет 1 кг?

2)  Сколько сантиметров в одном метре? Какую часть метра составляет 1 см?

3) Сколько ар в одном гектаре? Какую часть гектара составляет 1 а?

2) Закончи предложение:

a) 0,01 от тенге называется…        

b) 0,01 от метра называется…

c) 0,01 от дециметра называется…

d) 0,01 от гектара называется…

В процессе устного опроса совместно определить тему и цели урока/ЦО

Индивидуальная работа. Систематизация и обобщение ранее изученного материала. Повторение пройденного материала. Проведите фронтальный опрос и повторите правила:

1) как выразить процент в виде обыкновенной и десятичной дроби;

2) как выразить десятичные дроби в виде процентов;

3) как выразить обыкновенные дроби в виде процентов.

Приложение 2

Задание 1)

Задание 2) Запомни часто встречающиеся соответствия:

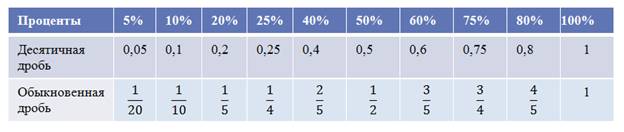
Задание 3) Запиши соответствия, заполнив пустые окошки:

Задание 4) Над процентами, как и над числами, можно производить арифметические действия. Проценты можно складывать и вычитать только с самими процентами. Помня об этом, выполни следующее задание.

На рисунке показан результат опроса среди учащихся, выраженный в процентах. Составь задачу и реши, приняв число всех опрошенных за 100%.

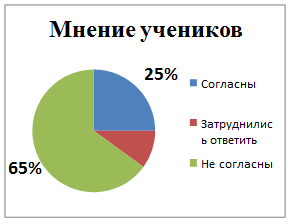
Выполнив письменные задания - Приложение 2, учащиеся менятся тетрадями и проверяют ответы по готовым ключам. Вопросы, вызвавшие затруднения у большинства учащихся, рассматриваются вместе с учителем.

Коллективная работа. Проценты выражаются дробями, поэтому задачи на проценты являются теми же задачами на дроби. Мотивировать учащихся на решение задач с помощью процентов: "Решая задачи на проценты ты становишься то экономистом, то бухгалтером, то мастером на заводе, то фермером, то бизнесменом..."

Решить типовые задачи.

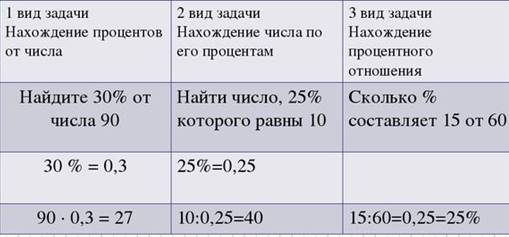
Сделать вывод, чтобы учащиеся вспомнили формулы для решения задач:

1)  ,   

2) ;

3)   и правила.

1) Чтобы найти процент от числа, надо:

а) выразить проценты обыкновенной или десятичной дробью (p%= 0,01p);

б) умножить данное число на эту дробь. b= a∙ 0,01- это основная формула процентов.

2) а) Чтобы найти число a по его части b, составляющей p%, надо b разделить на  . 

a= (b:p) ∙ 100 или

б) Чтобы найти число по его проценту, надо:

1) выразить проценты обыкновенной или десятичной дробью (р%=0,01р);

2) разделить часть данного числа на эту дробь:
 a = b: (0,01p).

3) Чтобы узнать, сколько процентов одно число (b) составляет от второго (a), надо первое число разделить на второе и результат умножить на 100%.

Увеличение числа на какое-то количество процентов: Чтобы увеличить на какое-то количество процентов число, мы переводим проценты в десятичную дробь, добавляем к ней единицу и умножаем на исходное число.

Образец: Увеличить 60 на

a)15%,                                                           b)115%

15% =0,15                                                     15% =1,15

1+0,15=1,15                                       1+1,15=2,15

60∙1,15=69                                                     60∙2,15=129

Уменьшение числа на какое-то количество процентов: Чтобы уменьшить число на какое-то количество процентов, мы переводим проценты в десятичную дробь, вычитаем из единицы и умножаем на исходное число.</MAIN >

Уменьши число 200 на: a) 35%,     b) 90%

Образец: Уменьшить 80 на 25%:   

25%=0,25, 

1- 0,25 = 0,75.

80 ∙ (1-0,25)= 80 ∙ 0,75=60.

Учителю при обсуждении задач необходимо акцентировать внимание учащихся на происходящие в задаче процессы для хорошего понимания использования процентов.

Работа в группе. Объединить учащихся в группы по 4 - 6 учеников произвольно (например: по сезонам дат рождения). Предложите задачи из учебного пособия номера или из Приложения 3, задания у всех групп одинаковые.

Задачи, решаемые по разным формулам. Попросите определить какая из них необходима при решении той или иной задачи. Формулы обозначить цифрами

  -1,   = - 2 и
  -3. Попросить проставить рядом с задачей тот или иной номер. Группа совместно сортирует задачи на три типа. Затем оценить - насколько правильно учащиеся делают выбор формул и предложить ученикам процесс взаимного обучения при решении практических задач: разобрать решение задачи в группе при возникновении вопроса по той или иной задаче, т.е. ученики будут выполнять задания индивидуально, но имеют возможность обсудить непонятные вопросы с товарищами.

Учащийся решает обязательно задачи каждого типа, записывая ход решения. Подвести итог после решения задач. Та группа, которая решила наибольшее количество задач, будет победителем. То есть таким образом проверяется сплоченность и организованность группы: если правильно разделить между членами группы задачи, то количество решенных задач будет больше. Сверить ответы. Задача разбирается у доски или в парах взаимопомощи, в зависимости от количества учащихся, несправившихся с ней.

Рефлексия

В конце урока учащиеся проводят рефлексию:

- Что вспомнил быстро, что с трудом вспомнил?

- Что осталось непонятным?

- Над чем необходимо работать и получить дополнительную консультацию.

Домашнее задание: тест.

Приложение 4

Выбери правильный ответ.

1.      Найди число, если 1 % его равен 75.

a) 0,75             b) 7,5               c) 7500                       d) 750)

2.      Вырази в процентах .

a) 0,9%           b) 90%            c) %             d) 9%

3.      В октябре 25% всех дней были дождливыми, 40% - пасмурными, остальные - солнечными. Сколько процентов дней в октябре были солнечными?

a) 75                b) 35                c) 65                d) 25

4.      В соревнованиях участвовало 500 школьников. Среди них 65% - мальчики. Сколько девочек участвовало в соревнованиях?

a) 390              b) 45                c) 210              d) 325

5.      Акгуль обещала решить 20 задач, из них она уже решила 13 задач. Сколько процентов всех задач Акгуль уже решила?

a) 0,65             b) 65                c) 6,5               d) 1,5

6.      На сколько процентов увеличится периметр квадрата, если его сторону увеличить на 30%?

a) 90%            b) 69%            c) 30                d) 70%

Дифференциация выражена в подборе заданий, в ожидаемом результате от конкретного ученика, в оказании индивидуальной поддержки учащемуся, в подборе учебного материала и ресурсов с учетом индивидуальных способностей учащихся. Более способным учащимся предлагаются задания второго уровня.           Предусмотрена самопроверка по ключу, в ходе которой ученики оценивают умение применять формулы.

В ходе коллективной деятельности при решении задач устно оценивается вычислительные навыки учащихся. Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, следить за безопасностью передвижения. При использовании ИКТ применять правила ТБ. Следить за осанкой учащихся.