55 Представление в виде Методическое указание Вариант 2

Методические рекомендации к уроку

Тема урока "Представление рационального числа в виде бесконечной десятичной периодической дроби"

Цели обучения:

6.1.2.18

распознавать, какие обыкновенные дроби представимы как конечные десятичные дроби;

6.1.2.19

представлять рациональное число в виде бесконечной периодической десятичной дроби;

6.1.2.20

находить период бесконечной периодической десятичной дроби;

Критерии оценивания

Учащийся:

знает:

·  как распознавать, какие обыкновенные дроби представимы как конечные десятичные дроби;

·  как представлять рациональное число в виде бесконечной периодической десятичной дроби;

·  как находить период бесконечной периодической десятичной дроби;

умеет:

·  распознавать, какие обыкновенные дроби представимы как конечные десятичные дроби;

·  представлять рациональное число в виде бесконечной периодической десятичной дроби;

·  находить период бесконечной периодической десятичной дроби;

Теоретический материал:

Несократимую дробь   можно преобразовать в десятичную только тогда, когда разложение знаменателя b на простые множители не содержит чисел, отличных от 2 и 5, т.е., некоторые обыкновенные дроби можно представить в виде конечных десятичных дробей, некоторые дроби невозможно представить конечной десятичной дробью.

Если в записи десятичной дроби одна цифра или группа цифр начинают повторяться бесконечно много раз, такую дробь называют периодической дробью.

В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Выполнить упражнения из Приложения 1.

1.      3аписать отношения в виде обыкновенной дроби и найти значение: 36:144; 60:5; 13:4; 17:13.

2.      Записать дробь в виде десятичной: ; ;;;.

3.      Записать дробь в виде обыкновенной: 0,1; 0,6; -5,15; -11,79; 4,165.

4.      Сократите дробь:

а)  = 1;      б)  =10;            в) =1.

5.      Решите уравнение:

а) ; б)  = .

Совместно с учащимися определить тему и цели урока, «зону ближайшего» развития.

Работа с классом. Вызов: в Приложении 1 в задании 1 не смогли найти точное отношение 17:13, а также в задании 2 записать дробь в виде десятичной . Как разрешить проблему?

Вспомним правило: Несократимую дробь   можно преобразовать в десятичную только тогда, когда разложение знаменателя b на простые множители не содержит чисел, отличных от 2 и 5, т.е., некоторые обыкновенные дроби можно представить в виде конечных десятичных дробей, некоторые дроби невозможно представить конечной десятичной дробью.

Вспомним как можно перевести обыкновенную дробь в десятичную.

Простые способы преобразования

Способ 1. Воспользуйтесь калькулятором, разделите числитель дроби на знаменатель в результате получите десятичную дробь.

Пример: Преобразовать дробь в десятичную дробь.

Решение: Разделим с помощью калькулятора числить на знаменатель, получим = 0,75.

Способ 2. Привести знаменатель дроби к 10, 100, 1000, 10000 и т.д.

1)      Найти число, которое преобразует знаменатель к числу из списка (10, 100, 1000, и т.д.).

2)      Умножить числитель и знаменатель на данное число.

3)      Записать числитель в виде десятичной дроби, расположив запятую (точку) в зависимости от количества нулей в знаменателе.

Пример: Преобразовать дробь  в десятичную.

Решение:

1)      Найдем число, на которое надо умножить числитель и знаменатель, чтобы в знаменателе получить  10, 100, 1000, 10000 и т.д., для этого делим 10, 100, 1000, 10000 на знаменатель, пока не получим целое число.

 - не целое,  - не целое, целое, число найдено.

2)   Умножим числитель и знаменатель на 125: .

Не все обыкновенные дроби можно представить в виде конечной десятичной дроби.

В этом вы уже убедились не раз.

Особое место среди всех дробей занимают периодические дроби – бесконечные числа, в то же время считающиеся рациональными, поскольку они могут быть переведены в обыкновенные дроби.

Правило: Если хотя бы один из множителей не является числом 2 или 5, то число нельзя перевести в конечную десятичную дробь.

Учитель, основываясь  на вышеозвученное правило в интерактивном режиме выводит вместе с учащимися правило перевода обыкновенной дроби в бесконечную десятичную дробь.

Если хотя бы один из множителей не является числом 2 или 5, то:

1)  делить числитель на знаменатель до тех пор, пока не станет ясно какая цифра или группа цифр повторяется бесконечно.

2) Записать десятичную дробь, заключив повторяющиеся цифры в скобки.

Правило: Если в записи десятичной дроби одна цифра или группа цифр начинают повторяться бесконечно много раз, такую дробь называют периодической дробью.

В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби.

Чистые периодические дроби и смешанные периодические дроби

Периодические дроби делятся на чистые и смешанные. Сам период представляет собой цифру или группу цифр, неизменно повторяющихся бесконечное количество раз в дробной части. У чистых периодических дробей период расположен сразу после запятой.

В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби.

Пример: В результате преобразования получается бесконечная периодическая десятичная дробь . Период равен 3. Читается ноль целых и три в периоде. Чистая периодическая дробь.

Пример: Дана дробь , в результате ее преобразования получается бесконечная периодическая десятичная дробь: . Период равен 7. Читается нуль целых две сотых и семь в периоде. Смешанная периодическая дробь.

Учащимся предложите: Составить задания на преобразование обыкновенной дроби в десятичную конечную, бесконечную: чисто и смешанно периодическую дробь и предложите соседу, затем сверьте свои результаты.

В процессе работы следить за тем, чтобы весь класс участвовал. Нескольким учащимся, кто раньше закончил, показать свои примеры у доски.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями. Приложение 2.

1)      Определить является ли дробь чисто периодической или смешанно периодической:

а) ;          б) ;   в) ;             г) ;            д) .

2) Записать период бесконечной десятичной дроби в скобках:

а) 0,72323..; б) 2,444…;  в) 0,817777…; г) -5,6666…; д) - 0,0202….

3) Выразить в виде периодической десятичной дроби:

а) ;              б) ;              в) -3;             г) ;             д) .

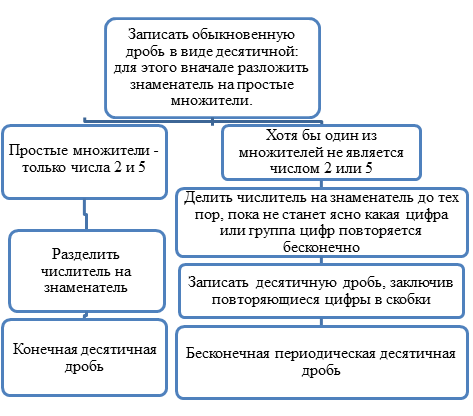
4) Составить алгоритм записи обыкновенной дроби в виде десятичной и оформить в виде блок – схем.

Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Помочь составить алгоритм записи в виде блок – схем. Можно задавать наводящие вопросы при затруднении.

Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Провести устный опрос по изученной теме:

1. Какую новую информацию получили о дробях: а) обыкновенных, б) десятичных?

2. Как можно перевести обыкновенную дробь в десятичную?

3. Что получили в результате?

4. Как называют полученные дроби?

5. Какие бесконечные дроби бывают?

6. Что называют периодом?

7. Как правильно читать периодические дроби?

Беседа. Рефлексия.

Обратите внимание на достижение целей обучения, которые поставлены вначале урока. урока.

•      Что вы узнали нового?

•      Что вам показалось интересным на уроке?

•      Какой вид работы понравился?

•      Какие задачи вызвали затруднения?

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в паре задания, самостоятельно выбирают уровень сложности.

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить период, выразить в виде периодической десятичной дроби обыкновенную дробь, является ли дробь чисто периодической или смешанно периодической, умение записать период бесконечной десятичной дроби в скобках.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В.