56 Перевод бесконечной Методическое указание Вариант 2

Методические рекомендации к уроку

Тема урока "Перевод бесконечной периодической десятичной дроби в обыкновенную дробь "

Цели обучения:

6.1.2.20

находить период бесконечной периодической десятичной дроби;

6.1.2.21

переводить бесконечную периодическую десятичную дробь в обыкновенную дробь;

Критерии оценивания

Учащийся:

знает:

·  как находить период бесконечной периодической десятичной дроби;

·  какие дроби называются чистыми или смешанными периодическими дробями;

·  как переводить бесконечную периодическую десятичную дробь в обыкновенную дробь;

умеет:

·  находить период бесконечной периодической десятичной дроби;

·  отличать чистые и смешанные периодические дроби;

· переводить бесконечную периодическую десятичную дробь в обыкновенную дробь.

Теоретический материал:

Если в записи десятичной дроби одна цифра или группа цифр начинают повторяться бесконечно много раз, такую дробь называют периодической дробью.

В краткой записи периодической дроби повторяющуюся цифру (или группу цифр) пишут в скобках. Эту цифру (или группу цифр) называют периодом дроби.

Чистые периодические дроби и смешанные периодические дроби

Периодические дроби делятся на чистые и смешанные, и они подчиняются разным алгоритмам перевода. Сам период представляет собой цифру или группу цифр, неизменно повторяющихся бесконечное количество раз в дробной части. У чистых периодических дробей период расположен сразу после запятой. Для них перевод в обыкновенную дробь заключается в том, что период записывается в числитель, а знаменатель состоит из количества цифр 9, равного количеству цифр в периоде.

В смешанных периодических дробях между запятой, отделяющей целую часть от дробной, и периодом могут присутствовать другие цифры. Смешанные периодические дроби следуют немного другим законам перевода в обыкновенные. Количество знаков в знаменателе остается равным количеству знаков после запятой, включая в период, но теперь знаменатель будет состоять не только из 9, но и из 0, где количество 9 – это количество цифр в периоде, а количество 0 – это количество цифр между запятой и периодом. Числитель же рассчитывается через разность числа записанного после запятой, включая период, и числа, представляющего набор цифр между запятой и периодом.

Пример: 

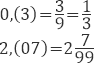
В смешанных периодических дробях между запятой, отделяющей целую часть от дробной, и периодом могут присутствовать другие цифры. Смешанные периодические дроби следуют немного другим законам перевода в обыкновенные. Количество знаков в знаменателе остается равным количеству знаков после запятой, включая в период, но теперь знаменатель будет состоять не только из 9, но и из 0, где количество 9 – это количество цифр в периоде, а количество 0 – это количество цифр между запятой и периодом. Числитель же рассчитывается через разность числа записанного после запятой, включая период, и числа, представляющего набор цифр между запятой и периодом. Пример: 

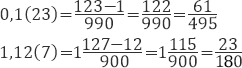
Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание. Провести опрос по теории: Как перевести обыкновенную дробь в десятичную? Какие десятичные дроби существуют? Привести примеры.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Индивидуальная работа. Для закрепления и оценки усвоения пройденного материала предложить следующие задания. Каждый выполняет самостоятельно.

Выполнить упражнения из Приложения 1.

1.      Записать дробь в виде обыкновенной:

2.      Записать дробь в виде конечной десятичной дроби:

3.      Записать дробь в виде бесконечной десятичной дроби:

4.      Определить: является ли дробь чисто или смешанно периодической:

a)    ; b) ; c) ; d) ; e)  

5.      Записать период бесконечной десятичной дроби в скобках

a)-3,037037…; b) 1,1212…; c) 4,151151…; d) 5,519519…

6.      Выразить в виде периодической десятичной дроби:

a)       ; b) ; c) ; d) .

После окончания выполнения, попросить обменяться тетрадями первый вариант со вторым. Взаимопроверка по ключу. Собрать информацию о выполнении.

Работа с классом. Вспомнить в процессе диалога, какие обыкновенные дроби представимы как конечные десятичные дроби, а какие невозможно представить конечной десятичной дробью. А также как представлять рациональное число в виде бесконечной периодической десятичной дроби (алгоритм), находить период бесконечной периодической десятичной дроби.

Рассмотреть на примере действие обратное изученному, т.е., перевод бесконечной дроби в обыкновенную дробь. Способ 1 – можно продемонстрировать блок –схему, затем разобрать алгоритм или в совместном диалоге вывести алгоритм, а затем составить блок – схему. Зависит от уровня обучаемости класса. Если слабый класс, то сначала продемонстрировать блок – схему и т.д.

Перевод бесконечной дроби в обыкновенную дробь.

Способ 1.

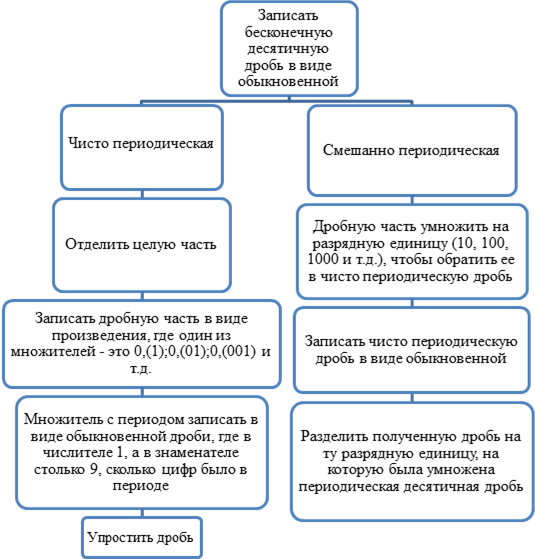
Способ 2

1. Посчитать, сколько цифр в периоде и после запятой, но до него.

2. Записать натуральным числом все цифры после запятой, включая период.

3. Записать натуральным числом все цифры после запятой до периода.

4. Записать разность этих двух натуральных чисел.

5. Разделить эту разность на число, в котором столько девяток, сколько цифр в периоде нашей дроби и столько нулей, сколько цифр до периода. Полученную дробь сократить – это дробная часть числа.

6. Целую часть числа надо добавить к полученной дробной части.

Пример 1: Представить бесконечную дробь  в виде смешанного числа.

1. В периоде две цифры (72), до периода цифр нет (0).

2. Записываем период натуральным числом – 72. Записываем натуральным числом цифры до периода – 0.

3. Считаем разность этих чисел: .

4. Делим эту разность на число: 99 – в нем две девятки (по числу цифр периода) и нет нулей, так как до периода в числе никаких цифр нет:  – это дробная часть.

5. Добавляем целую часть к дробной и получаем результат:

Пример 2: Представим в виде смешанного числа дробь 1,791666…=1,791(6).

1. В периоде одна цифра (6), до периода три цифры (791).

2. Записываем цифры после запятой, включая период, натуральным числом – 7916. Записываем натуральным числом цифры до периода – 791.

3. Считаем разность этих чисел:

4. Делим эту разность на число 9000 – в нем одна девятка (по числу цифр периода) и три нуля, так как до периода в числе три цифры: – это дробная часть.

5. Добавляем целую часть к дробной и получаем результат:  .

Пример 3: Представим в виде обыкновенной дроби число 0,6428571428571…=0,6(428571).

1. В периоде 6 цифр (428571), до периода одна цифра (6).

2. Записываем цифры после запятой, включая период, натуральным числом – 6428571. Записываем натуральным числом цифры до периода – 6.

3. Считаем разность этих чисел: 6428571 – 6= 6428565.

4. Делим эту разность на число 9999990 – в нем шесть девяток (по числу цифр периода) и один ноль, так как до периода в числе одна цифра:

 – это результат, так как у числа не было целой части.

Групповая работа.

Объединить учащихся в разноуровневые группы по 4 - 6 учеников. Раздать каждой группе карточки с заданиями. Приложение 2.

1) Определить является ли дробь чисто периодической или смешанно периодической и перевести в обыкновенную:

a); b) ; c) ; d)  

2) Записать период бесконечной десятичной дроби в скобках и перевести в обыкновенную:

a) 1,3333…; b) 1,5555…; c) 1,6666…; d) 3,231231…; e) 2,212212…

3)

Дополнительное задание:

4) Вычислить: 0,(45) + 0,(3) +  = 

5) Найди закономерность: ; ; ;  

Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения задания.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия. Подвести итог урока, определить отношение учащихся, их понимание темы. Разместить стикеры с именем под картинками по окончании урока.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в группе задания, самостоятельно выбирают уровень сложности.

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить период, определять является ли дробь чисто периодической или смешанно периодической, умение записать период бесконечной десятичной дроби в скобках, выразить периодическую десятичную дробь в виде обыкновенной дроби.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В.