62 Решение текстовых задач. Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока "Решение текстовых задач"

Цели обучения:

6.5.1.4  решать текстовые задачи с рациональными числами.

Критерии оценивания

Учащийся:

знает:

·         как решать текстовые задачи с рациональными числами;

умеет:

·         составлять математические модели при решении текстовых задач с рациональными числами;

·         решать текстовые задачи с рациональными числами;

·         обосновывает свое решение.

Теоретический материал:

Решить задачу арифметическим методом - значит найти ответ на требование задачи с помощью арифметических действий над значениями, указанными в задаче. Используя известные формулы при решении задач и, используя известные свойства умножения и действия, решить задачу.

Выполняя решение задачи, нужно провести анализ текста задачи и последовательно ответить на вопросы:

1. Какие величины надо знать, чтобы ответить на вопрос задачи?
2. Какая из величин известна, а какая нет?

3. Что нужно знать, чтобы найти эту величину?

4. Как это узнать, исходя из условия задачи?

Ход урока

Организационный момент. Мотивация к учебной деятельности.

Проверка домашнего задания.

Выполнить устно:

Приложение 1

1) Найдите значение выражения 8,65 – (– (–х)) – 4,2 при х = 2,34.

Ответ: 2,11.

2) Найдите сумму всех целых чисел n таких, что –10 < n < 12,3.

Ответ: n = 33.

3) Точки заданы своими координатами: О(0), М(m), N(n). Определите знак числа m, если при сравнении длины отрезков выражены неравенством: OM > ON,  а координаты  m < n.

Ответ: m < 0.

4) Посев семян моркови рекомендуется проводить при дневной  температуре воздуха не менее +12°С. На рисунке показан прогноз дневной температуры воздуха в первые три недели мая (точки, указывающие значение температуры, для наглядности соединены линией). Определите, в течение скольких дней за этот период можно будет производить посев семян  моркови, если прогноз окажется верным.

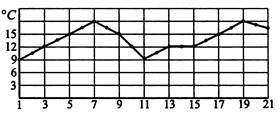
Ответ: 7 дней.

5) Выберите из числовых равенств правильный ответ для следующего выражения: удвоенная сумма чисел  и  равна частному от деления разности чисел 0,5  и (–0,1) на число 0,1.

а)                 б))

в)         г)

Ответ: б.

Совместно с учащимися определить тему и цели урока, «зону ближайшего развития».

Индивидуальная работа.  Организуйте любую игру, предусматривающую соревновательный момент и скорость ответа. Предложите учащимся выполнить задания из Приложения 2 для повторения опорных знаний из пройденного материала.

Приложение 2

Выбери правильный ответ.

1. Выражение, содержащее буквы, называется ... выражением.

a) целым; b) числовым; c) буквенным.

2. Запишите выражение: частное суммы чисел -103 и -47 и числа 15.

a) (-103 + (-47)) : 15; b) 103 – 47 : 15;

c) (103 – 47) : 15.

3. Найди значение выражения 5а – 12 при а = 30.

a) 143; b) 138; c) 120.

4. Сочетательное свойство сложения:

a) a ∙ b = b ∙ a;

b) a + b = b + a;

c) (a + b) + c = a + (b + c).

5. Упрости выражение, используя переместительное и сочетательное свойства сложения: (45 + х) + 16.

a) 16x + 45;                b) 45x + 16;               c) x + 61.

6. Упрости выражение, используя переместительное и сочетательное свойства умножения: 125∙х ∙ 8.

a) 133x; b) 1000x; c) 133 + x.

7. Чтобы умножить разность двух чисел на третье число, нужно умножить ... на это число и из первого произведения вычесть второе.

a) каждое слагаемое;

b) уменьшаемое и вычитаемое;

c) само это число.

8. Запиши данное выражение в виде суммы, используя распределительное свойство умножения: 25 ∙ (3 + х).

a) 25 + 3х; b) 75 + 25x; c) 28 + x.

9. Запиши выражение в виде произведения: 6с – 12.

a) 8c; b) 2 ∙ (c + 2); c) 6 ∙ (c – 2).

10. Уравнением называют ..., содержащее букву, значение которой надо найти.

a) неравенство;

b) произведение;

c) равенство.

11. Реши уравнение: 37 – 3х = 10.

a) 27; b) 10; c) 9.

12. Реши уравнение: 64 + 36 : (x ∙ 3 – 15) = 70.

a) 7; b) 12; c) 6.

13. Составь уравнение к решению задачи:

На рисунке изображены треугольники и четырехугольники. Сколько тех и других изображено на рисунке, если у всех фигур вместе 69 углов, а всего фигур - 18?

a) 4x + (18 – x ) ∙ 3 = 69;

b) 4x + (69 – x ) ∙ 3 = 18;

c) (4x + 3x ) ∙ 18 = 69.

Изучение нового материала. Работа с классом.

Существуют различные методы решения текстовых задач: арифметический, алгебраический, графический, геометрический. Причем, задача по выбранному методу может быть решена различными способами. Рассмотрим один из методов.

Решить задачу арифметическим методом - значит найти ответ на требование задачи с помощью арифметических действий над значениями, указанными в задаче.

Выполняя решение задачи, нужно провести анализ текста задачи и последовательно ответить на вопросы:

1. какие величины надо знать, чтобы ответить на вопрос задачи?

2. Какая из величин известна, а какая нет?

3. Что нужно знать, чтобы найти эту величину?

4. Как это узнать, исходя из условия задачи?

Решить с учащимися задачи на повторение. В зависимости от обучаемости класса, задачи можно решить устно, записать только 6 и 7 задачи.

Приложение 3

Пример 1: Два велосипедиста выехали одновременно навстречу друг другу с одинаковой скоростью. Через какое время они встретятся, если расстояние между ними - 72км, а скорость - 12 км/ч?»

Решение.

1. Какова скорость сближения велосипедистов? 12 + 12 = 24 км/ч.

2. Через какое время велосипедисты встретятся? 72 : 24 = 3 ч.

Ответ: велосипедисты встретятся через 3 часа.

Пример 2: В первый день продали 25 кг яблок, во второй - 40 кг, а в третий день продали 55 кг яблок. Сколько всего яблок продали за три дня?

Решение: 25 + 40 + 55 = 120 кг.

 Ответ: всего яблок продали за три дня 120 кг.

Пример 3: В одном куске — 150 м проволоки, а в другом — на 35 м меньше. Сколько метров проволоки в двух кусках вместе?

Решение:

1. Сколько метров проволоки во втором куске?

150 − 35 = 115 м.

2. Сколько метров проволоки в двух кусках вместе?

150 + 115 = 265 м.

Ответ: проволоки в двух кусках вместе — 265 м.

Пример 4: Двадцать ящиков весят 3 т. Сколько килограммов весит один ящик?

Решение:

3 т : 20 = 3000 кг : 20 = 150 кг.

Ответ: один ящик весит 150 кг.

Пример 5: В первый день бригада собрала 700 кг картофеля, а во второй день — в 2 раза больше, чем в первый. На сколько килограммов картофеля больше бригада собрала во второй день?

Решение:

1. Сколько килограммов картофеля собрала бригада во второй день?

700⋅2=1400 кг.

2.  На сколько килограммов картофеля больше собрала бригада во второй день?

1400 − 700 = 700 кг.

Ответ: на 700 кг картофеля больше собрала бригада во второй день.

Пример 6: На первой полке стояло в 3 раза больше книг, чем на второй. На двух полках вместе стояло 120 книг. Сколько книг стояло на каждой полке?

Решение:

1. сколько частей приходится на все книги?  1 + 3 = 4 части.

2. Сколько книг приходится на одну часть? 120 : 4 = 30 книг — число книг на второй полке.

3.  Сколько книг стояло на первой полке? 30⋅3=90 книг.

Ответ: 90 книг стояло на первой полке, 30 книг стояло на второй полке.

Пример 7: Два велосипедиста выехали одновременно навстречу друг другу с одинаковой скоростью.

Пример. Чтобы доставить письмо за 2 часа 40 минут из А в В, расстояние между которыми 70,5 км, почтальон ехал сначала на велосипеде со скоростью 12,75 км/ч, а затем на мотоцикле со скоростью 67,5 км/ч. Сколько времени ехал почтальон на велосипеде и сколько на мотоцикле?

Решение:

1)  (км) - проехал бы почтальон, если бы все 2 часа 40 минут ехал на велосипеде;

2)  

70,5 - 34 = 36,5 (км) - расстояние, которое осталось бы проехать на мотоцикле;

3)  (км/ч) - разность скоростей мотоцикла и велосипеда;

67,5 - 12,75 = 54,75(км/ч) - разность скоростей мотоцикла и велосипеда;

4)  (ч) - он ехал на мотоцикле;

5)  (ч) - ехал на велосипеде.

Ответ: 2 ч;  ч.

Эту же задачу, позже, мы решим с по мощью уравнений.

Провести тренинг на решение задач.

Приложение 4

Реши задачи арифметическим методом:

1) В классе 27 учеников. Четыре девятых из них девочки, а треть мальчиков носят очки. Сколько мальчиков носят очки?

Ответ: 5 мальчиков.

2) Три школьника купили одинаковые тетради. Один из них купил 5 тетрадей, второй - 3 тетради, третий - 4 тетради. Всего они уплатили 399 тенге. Сколько денег заплатил каждый?

Ответ: 1) 5 + 3 + 4 = 12 (шт.) – всего купили тетрадей;

 2) 399 : 12 = 33,25 (тг) – цена одной тетради;

3) 33,25 • 5 = 166,25 (тг) – заплатил первый школьник;

4) 33,25 • 3 = 99,75 (тг) – заплатил второй школьник;

5) 33,25 • 4 = 133 (тг) – заплатил третий школьник.

3) Читальный зал имеет размеры 9,6 м × 5 м ×4,5 м. На сколько мест рассчитан читальный зал, если на каждого человека необходимо 3 куб. м воздуха?

Ответ: 72 человека.

4) Бассейн наполняется двумя насосами различной мощности. Первый насос, работая один, может наполнить бассейн за 3,2 часа, а второй за 4 часа. За сколько времени наполнится бассейн при одновременной работе этих насосов? (Ответ округлить с точностью до 0,1.)

Ответ: 1,8 часа

Закрепление нового материала. Групповая работа.

На данном этапе урока у учащихся развивается умение сотрудничать с одноклассниками и учителем при совместной работе, умение прислушиваться к мнению других.

Разделите учащихся на группы по уровню усвоения знаний (базовый, средний, продвинутый). Каждая группа получает задания. Решая задания, учащиеся закрепляют вычислительные навыки, умение решать примеры на все действия. Задания у всех групп одинаковое. Предложить ученикам выбрать уровень сложности задания на более высоком уровне.

Приложение 5

После выполнения заданий, учащиеся проводят взаимопроверку правильности выполнения заданий по образцу, выданному учителем. Если в классе несколько одинаковых групп по уровням усвоения, то можно провести взаимопроверку групп.

Ответы:

Вопросы  учителя:

·         Все ли задания выполнили?

·         Какие задачи вызвали затруднения?

·         Как вы пытались найти решения таких задач?

Беседа. Рефлексия.

Обратите внимание на достижение целей обучения, которые поставлены вначале урока. урока.

•      Что вы узнали нового?

•      Что вам показалось интересным на уроке?

•      Какой вид работы понравился?

•      Какие задачи вызвали затруднения?

Домашнее задание: примеры и задачи из уровня В учебного пособия "Математика 6"№...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в группе задания, самостоятельно выбирают уровень сложности.

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение провести анализ, синтез задачи, производить арифметические действия, применять свойства действий.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В.