6.4D-5. Фигуры в пространстве. Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока " Расположение фигур в пространстве. Изображение пространственных фигур, «невидимые» линии. Понятие вектора "

Цели обучения:

6.3.2.4

распознавать фигуру по её изображению и изображать плоские и пространственные фигуры;

6.3.4.1

знать определение вектора и уметь изображать его.

Критерии оценивания

Учащиеся:

- комментируют  построение развёрток;

- описывают выбор изображения фигуры при повороте;

- обосновывают построение видов сверху, спереди, слева;

- знают определение вектора и умеют изображать его;

- различают скалярные и векторные величины.

Ход урока

Организационный момент.

Проверить домашнее задание. При необходимости разобрать примеры, вызвавшие затруднения.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Актуализация опорных знаний. Развитие пространственного мышления.

Приложение 1.

 Дайте ответ на вопросы.

1. Сидя за партой в кабинете, укажите тела, относительно которых вы двигаетесь.

2. Движутся или находятся в покое относительно друг друга люди, стоящие на двух одинаково поднимающихся эскалаторах метро?

3. Почему в тумане, не видя берегов реки, нельзя понять, в каком направлении движется лодка?

4. Розыскная собака идет по следу. Чью траекторию движения она повторяет?

5. Приведите примеры тел, которые участвуют в равномерном движении.

Наблюдайте за работой учащихся, если необходимо корректируйте их деятельность.

Взаимопроверка по окончанию.

Работа с классом. Повторение понятий прошлого урока:

– перемещение;
– траектория;
– путь.

и еще раз подвести итог.

Чем же отличается путь от перемещения?

Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия:

1.      Путь – скалярная величина и характеризуется только числовым значением.

2.      Перемещение – векторная величина и характеризуется как числовым значением (модулем), так и направлением.

3. При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
4. Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.

Упражнения и вопросы для повторения.

1. Путь или перемещение мы оплачиваем при поездке в такси? (Путь)
2. Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. найти путь и перемещение мяча. (Путь – 4 м, перемещение – 2 м.)

Подготовить сообщение обобщающее тему и небольшой исторический экскурс по теме "Фигуры в пространстве". Можно предварительно дать задание учащимся, чтобы они собрали материал и дать возможность презентовать свои сообщения.

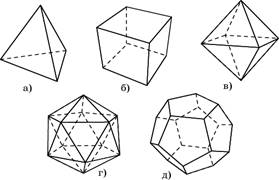Правильные многогранники были известны еще в древней Греции. Пифагор и его ученики считали, что все состоит из атомов, имеющих форму правильных многогранников. В частности, атомы огня имеют форму тетраэдра (его гранями являются четыре правильных треугольника (рис. а); земли - гексаэдра (куб – многогранник, гранями которого являются шесть квадратов, рис. б); воздуха – октаэдра (его гранями являются восемь правильных треугольников, рис. в); воды – икосаэдра (его гранями являются двадцать правильных треугольников, рис. г); вся Вселенная, по мнению древних, имела форму додекаэдра (его гранями являются двенадцать правильных пятиугольников, рис. д).

Групповая работа. Для выполнения следующих упражнений разделите учащихся на малые группы, для того чтобы они обсудили задание и выполнили его совместно. При выполнении задания учащиеся анализируют условие, в ходе обсуждения развивают математическую речь, самостоятельно принимают решение, развивают навыки работы в команде.  

Приложение 2

Практическая работа.

Задание 1.

а) Рассмотрите многогранники и заполните следующую таблицу, в которой В – число вершин, Р – число ребер, Г – число граней многогранника.

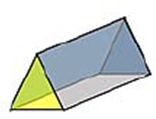
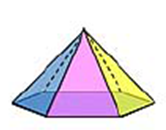
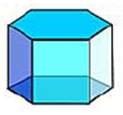
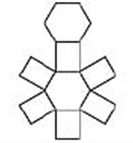
б) Определите для каждой строки значение алгебраической суммы: В - Р + Г.

в) Выведите общие формулы для а) n-угольной пирамиды; б) n-угольной призмы.

Вывод: Из приведенной таблицы непосредственно видно, что для всех выбранных многогранников имеет место равенство В - Р + Г = 2. Оказывается, что это равенство справедливо не только для рассмотренных многогранников, но и для произвольного выпуклого многогранника. Впервые это свойство выпуклых многогранников было доказано Леонардом Эйлером в 1752 году и получило название теоремы Эйлера.

Задание 2.

Векторы с равными модулями и одинаковыми направлениями называются равными векторами.

От любой точки М можно отложить вектор, равный данному вектору, и при том только один.

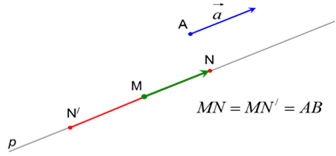
Постройте вектор  и постройте на прямой  несколько ему равных векторов. Опишите построение и сделайте вывод.

Наблюдайте за работой учащихся, если необходимо корректируйте их деятельность.

По окончании времени каждая группа представляет свою работу классу.

Работа в парах. (При наличии времени). Учебное пособие «Математика 6». Решить задачи по учебнику на изучаемую тему: "Расположение фигур в пространстве. Изображение пространственных фигур, «невидимые» линии". Задания по цели обучения на повторение основных знаний, полученных по теме, оформляя их в соответствии с требованиями. Взаимооценивание: ученики оценивают доступность объяснения при взаимообучении. Взаимопроверка по ответам.

Рефлексия.

По итогам полученных ответов примите решение о повторном изучении, закреплении темы или продолжении изучения материала по программе.

Домашнее задание.  Обязательное домашнее задание по целям обучения 6.3.2.4, 6.3.4.1

 «Фигуры в пространстве и понятие вектора» предполагает количество заданий, на выполнение которых учащиеся должны затрачивать не более 15-20 минут. Задания для выполнения дома рекомендуем дифференцировать по уровню сложности, включая задания на анализ, синтез и оценку. При этом, желательно, давать учащимся задачи практического содержания: решить из уровня В учебного пособия «Математика 6» №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.