6.4В-15.Прямая пропорциональность. Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока "Прямая пропорциональность и её график"

Цели обучения:

6.1.2.23

распознавать прямо пропорциональные зависимости и приводить примеры;

6.2.1.12

знать формулу и строить график прямой пропорциональности;

6.5.2.11

интерпретировать графики реальных зависимостей между прямо пропорциональными величинами;

6.5.2.12

записывать формулу прямой пропорциональности по описанию;

6.5.2.13

строить график прямой пропорциональности;

Критерии оценивания

Учащиеся:

знают

·         как распознать прямо пропорциональные зависимости и привести примеры;

·         как по формуле строить график прямой пропорциональности;

умеют

·         интерпретировать графики реальных зависимостей между прямо пропорциональными величинами;

·         записывать формулу прямой пропорциональности по описанию;

·         строить график прямой пропорциональности;

Теоретический материал:

Определение. Две величины называются прямо пропорциональными, если их отношение равно конкретному, отличному от нуля числу, то есть: , тогда .

Определение. Зависимость вида y=kx называется прямой пропорциональностью.

Число k называется коэффициентом пропорциональности.

Ход урока

Организационный момент.

Проверить домашнее задание. При необходимости разобрать примеры, вызвавшие затруднения.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Актуализация опорных знаний. Фронтальный опрос. Следить за активностью класса.

Приложение 1.

Задание 1.

Из приведённых ниже формул выпишите формулы, которые являются прямой пропорциональностью и запишите, что является их графиком:

P = 5,2b;         K = ;                        a = ;              M = m : 5;       G = ;

a = 8g + 1;      c = 4 : d;         s = vt;  ab = 18;           S = a²

Прямая пропорциональность:

P = 5,2b;    K = ;    M = m : 5

график — луч с началом в начале координат.

Задание 2.

Две величины  a  и b прямо пропорциональны. Заполните таблицу соответствующих значений этих величин.

Работа с классом. Вывести с учащимися в совместном диалоге свойства зависимости прямая пропорциональность и ее графика.

Сформулируем свойства прямой пропорциональности:

1) График любой такой прямой проходит через начало координат, так как в уравнении  при   независимо от значения   будет равен нулю;

2) Прямые не будут параллельны, так как их угловые коэффициенты не равны.

3) Для построения каждого графика нам достаточно выбрать одну точку, так как вторая уже известна – это точка (0; 0).

Итак, для первого графика возьмем точку (1; 1)

Для второго графика возьмем точку (1; 2)

Для третьего графика (1; -1)

Для четвертого (1; -2)

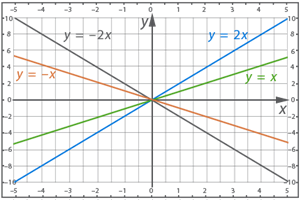
4) По графику очень хорошо видно, что прямая y=2x пошла круче, чем прямая y=x, угол прямой y=2x менее острый, при одинаковых значениях аргумента значение функцииy=2x больше чем y=x, но в обоих случаях угол острый и функция возрастает.

Обе прямые y=-2x и y=-x имеют тупой угол наклона, обе функции убывают, но у прямой y=-2x менее тупой и эта функция убывает быстрее.

Дальнейшее изучение и закрепление провести в группах.

Групповая работа. Для выполнения следующих упражнений разделите учащихся на малые группы, для того чтобы они обсудили задание и выполнили его совместно. При выполнении задания учащиеся анализируют условие, в ходе обсуждения развивают математическую речь, самостоятельно принимают решение, развивают навыки работы в команде.

Приложение 2

Задание 1. Определить соотношение между угловыми коэффициентами на рисунке, если единичный отрезок равен 1 клетке и сделать вывод:

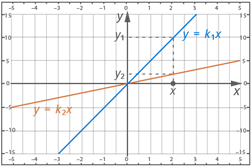
 отсюда 

Задание 2. Построить график прямой пропорциональности, если известно, что ему принадлежит точка с координатами (2; 8)

Решение: 1) Для построения прямой нам нужно две точки, первая из них (0; 0), так как все графики прямой пропорциональности проходят через точку (0; 0), а вторая точка задана – это точка (2; 8).

2) Можно поступить иначе. Из заданной точки (2; 8) мы понимаем, что х=2 и у=8 удовлетворяет нашему уравнению вида y=kx, подставим эти значения и найдем k: 8=2k, отсюда k=4. Итак, нам задано уравнение y=4x, которое легко можно построить.

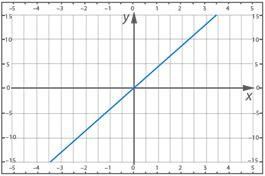
Задание 3. Построить график прямой пропорциональности y=0.4x и по нему ответить на следующие вопросы.

Решение:  Построим график. Первая точка нам известна – для любого графика прямой пропорциональности это точка (0; 0). Для второй точки возьмем x=10, тогда y=4:

а) По графику требуется определить значение функции при следующих значениях аргумента:  x=0, x=5, x=10, x=-5;

б) по заданному значению функции определить значение аргумента: y=8.

Решение: 8=0,4x, 80=4x, x=20.

в) Определить по графику решение неравенств: 0,4x<0; 0,4x>0.

Решение:

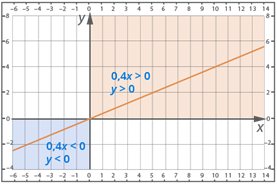
y<0 при x<0

y>0 при x>0

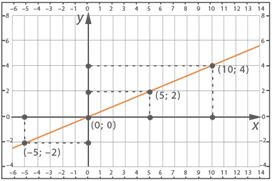
Задание 4. По заданному графику определить угловой коэффициент.

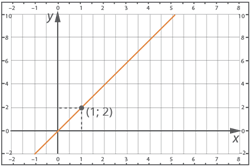
Решение: По графику видно, что он проходит через точку (1; 2), значит пара чисел х=1, у=2 удовлетворяет функции вида y=kx, значит, можем подставить значения в уравнение и найти k: 2=k∙1, k=2. Значит нам задан график функции y=2x.

Задание 5. График функции y = kx проходит через точку A (3; 6). Принадлежит ли графику этой функции точка:

а) B(-6; -3); б) C(4; 8); в) D(-1; -2); г) M(0; 0)?

Выполнив задания, сделать выводы, ответив на следующие вопросы.

1.    Через какую точку всегда проходит график прямой пропорциональной зависимости?

2.    При каких значениях углового коэффициента график прямой пропорциональной зависимости y = kx возрастает?

3.    При каких значениях углового коэффициента график прямой пропорциональной зависимости y = kx убывает?

4.    Как ведет себя график при увеличении углового коэффициента в плюс бесконечность?

5.    Как ведет себя график при приближении углового коэффициента к нулю?

6.    Какую формулу имеет прямая пропорциональная зависимость, график которой находится в первом и третьем координатных углах?

7.    Какую формулу имеет прямая пропорциональная зависимость, график которой находится во втором и четвертом координатных углах?

Наблюдайте за работой учащихся, если необходимо корректируйте их деятельность. По окончании времени каждая группа представляет свою работу классу.

Работа в парах.  Учебное пособие «Математика 6». Решить задачи по учебнику на изучаемую тему: задания по цели обучения 6.1.2.23, 6.2.1.12, 6.5.2.11, 6.5.2.12, 6.5.2.13

«Прямая пропорциональность и её график», на повторение основных знаний, полученных по теме, оформляя их в соответствии с требованиями. Взаимооценивание: ученики оценивают доступность объяснения при взаимообучении. Взаимопроверка по ответам.

Рефлексия. Для формативного оценивания примените технику «Светофор».

Попросите учащихся показать карточками сигналы, обозначающие их понимание или непонимание материала, затем задайте вопросы в соответствии с тем, какие карточки подняты учащимися. По итогам полученных ответов примите решение о повторном изучении, закреплении темы или продолжении изучения материала по программе.

Домашнее задание.  Обязательное домашнее задание по целям обучения 6.1.2.23, 6.2.1.12, 6.5.2.11, 6.5.2.12, 6.5.2.13 «Прямая пропорциональность и её график» предполагает количество заданий, на выполнение которых учащиеся должны затрачивать не более 15-20 минут. Задания для выполнения дома рекомендуем дифференцировать по уровню сложности, включая задания на анализ, синтез и оценку. При этом, желательно, давать учащимся задачи практического содержания: решить из уровня В учебного пособия «Математика 6» №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.