68 Раскрытие скобок. Коэффициент. Метод

Методические рекомендации к уроку

Тема урока "Раскрытие скобок. Коэффициент. Подобные слагаемые. Приведение подобных слагаемых "

Цели обучения:

6.2.1.5

знать правила раскрытия скобок;

6.2.1.6

знать определения понятий коэффициента, подобных слагаемых;

6.2.1.7

приводить подобные слагаемые в алгебраических выражениях;

Критерии оценивания

Учащийся:

знает:

·         правила раскрытия скобок;

·         определения понятий коэффициента, подобных слагаемых.

умеет:

·         приводить подобные слагаемые в алгебраических выражениях.

Теоретический материал:

Распределительное свойство умножения относительно сложения:

Следовательно, для любых чисел a, b и m верно равенство:

m· (a + b) = m ·a + m ·b  или (a + b) · m = a · m + b · m

выражающее распределительное свойство умножения.

Распределительное свойство умножения относительно вычитания:

Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

m · (a - b)   m · a – m · b или (a - b) · m = a · m – b · m

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

Устный опрос:

1) Что называется алгебраическим выражением и переменной?

2) Как вычислить значение алгебраического выражения при данных значениях переменных?

Озвучь:

а) распределительный закон умножения,

б) правило знаков.

Совместно с учащимися определить тему и цели урока, «зону ближайшего» развития.

Индивидуальная работа. Контроль усвоения материала (письменный опрос).

Выполнить задания на повторение из Приложения 1 индивидуально по вариантам.

Приложение 1.

Вариант 1

1. Было закуплено 5 телевизоров стоимостью  тенге, 7 приемников стоимостью  тенге и 8 магнитофонов стоимостью  тенге. Напишите алгебраическое выражение для вычисления стоимости покупки и найдите его значение при
.

2. Найдите значение выражения , если   y.

3. Найти допустимые значения переменных:

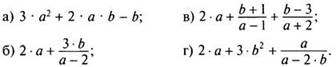
Вариант 2

1. Было закуплено 7 телевизоров стоимостью  тенге, 6 приемников стоимостью  тенге и 5 магнитофонов стоимостью  тенге. Напишите алгебраическое выражение для вычисления стоимости покупки и найдите его значение при
.

2. Найдите значение выражения , если  и .

3. Найти допустимые значения переменных:

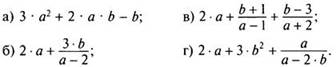
Взаимопроверка по кодам ответов. Разобрать последнее задание подробно с классом.

Работа с классом. I) Совместно с учащимися в интерактивном режиме изучить новую тему.

Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом (или просто коэффициентом).

Например: ;  5- коэффициент.

Коэффициент обычно пишут перед буквенными множителями.

Коэффициентом такого выражения, как   или , считают 1, так как: ; .

При умножении –1 на любое число  получается число , т.е.: .

Поэтому числовым коэффициентом выражения  считают число –1

Упростить выражение: , коэффициент (-0,21).

Задание. Упростить выражение и подчеркнуть коэффициент:

а)– 2,7 ∙ a ∙ 10; коэффициент равен -27

б) ; коэффициент -25

в) ; коэффициент равен 2

Вспомним еще раз правило знаков, стоящих перед скобками.

Рассмотрим выражения:  и .

Чем они отличаются? (Они отличаются только знаками, стоящими перед скобками).

Вспомнив правила прибавления суммы к числу и вычитания суммы из числа, произвести преобразования совместно с учащимися.

 и .

Сравнить полученные выражения и сделать вывод.

Вывод: Если перед скобками стоит знак «+», то при раскрытии скобок знаки слагаемых в скобках сохраняются.

Если перед скобками стоит знак «-», то при раскрытии скобок знаки слагаемых в скобках меняются на противоположный.

II) Составить буквенные выражения, к каждому правилу, дать задание соседу. Совместно с соседом обсудить решение примера.

Пример:             

Проверим: Как будет работать распределительное свойство умножения числа на сумму при умножении на:

а) положительное число? б) отрицательное число?

Проверить на частных примерах и сделать вывод.

Пример:                   .

 Вывод: а) При умножении на положительное число знаки слагаемых не изменяются.

 б) При умножении на отрицательное число изменяются на противоположное.

То есть получили, что при умножении суммы на число применяются те же правила раскрытия скобок, что мы вывели.

Переход от умножения:  и  соответственно к сложению и вычитанию:  называется раскрытием скобок.

III) а) Открыть учебное пособие "Математика 6", прочитать теорию к теме, сравнить свои составленные определения с текстом, оценить правильность рассуждений, при необходимости - откорректироать информацию. Закрепить выведенные правила на примерах. б)) Решить задания из учебного пособия «Математика 6» по данной теме уровня В, применив прием «Активный класс», проверить решения по заготовленным ответам.

Групповая работа. С целью дальнейшего закрепления и углубления темы провести работу в группах. Объединить учащихся в разноуровневые малые группы. Раздать задания. Можно для каждой группы дать разные варианты заданий. Если раздать одинаковые задания, то между группами можно провести взаимопроверку.

Приложение 2.

1. Раскройте скобки:

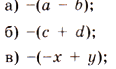
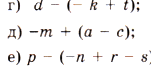
2. Раскройте скобки и найдите значение выражения:

              .

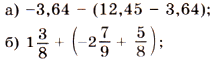
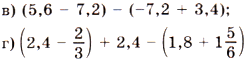3. Упростите выражение:

                         .

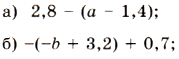
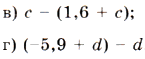4. Дополнительные задания:

Решите уравнения, предварительно упростив:

               .

Можно в зависимости от обучаемости класса дать меньше подпунктов в каждом заданий.

Учитель проходит по рядам, слушает, при необходимости корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям.

Каждая группа демонстрирует свой результат выполнения задания.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости). Ученики, распределяя в паре задания, самостоятельно выбирают уровень сложности. Предусмотрена самопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить правильно решение, навыки устного счета, умение производить арифметические действия, умение применять правило знаков, распределительный закон умножения, правильно применять правила, изученные на даном уроке. Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

"Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

"Математика 6", Алдамуратова Т.А, Байшоланов Т.С.;

Самостоятельные и контрольные работы, Ершова А.П., Голобородько В.В.