8. Методические рекомендации к проведению урока. Вариант 2.

Методические рекомендации к уроку

Тема урока: «Прямая пропорциональность и ее график».

Цели обучения:

Учащиеся:

6.2.1.12 знать формулу и строить график прямой  пропорциональности;

6.5.2.13 строить график прямой пропорциональности.

Критерии оценивания:

Учащиеся достигнут цели, если

·        знают формулу прямой  пропорциональности;

·        строят график прямой пропорциональности.

1.   Организационный момент.

2.   Проверка домашнего задания.

3.   ФО по цели прошлого урока

Проверка ФО: Взаимопроверка в парах по посадке по слайдам.

Учитель у себя фиксирует результаты.

Учащийся достиг цели, если

- распознает прямо пропорциональные величины;

- находит формулы, имеющие переменные в прямо пропорциональной зависимости;

- находит формулы, не имеющие переменные в прямо пропорциональной зависимости;

4.   Объявление цели урока  и обсуждение критериев оценивания.

Предлагаю начать урок с изречения, которое придаст уверенность, деловой настрой и позитив настроения. Для этого решим пропорцию и найденные числа заменим соответствующей буквой. Учащимся раздаются карточки с заданиями (количество карточек можно распечатать на количество учащихся, несколько учащихся будут иметь одинаковые задания, здесь кто первый вычислит, его ответ – зачтется при угадывании высказывания).

При выполнении этого задания было использовано знание свойства пропорции ( при необходимости повторяем свойство пропорции для тех учащихся, которые забыли это свойство)

ФО: учитель отмечает у себя учащихся быстро и правильно выполнивших задания.

Результаты заданий можно использовать для деления на группы: 1 группа – четные числа первой десятки, 2 группа – нечетные числа второй десятки, 3 группа – числа, большие десяти. (по усмотрению учитель сам выбирает критерии для деления на группы в зависимости от числа учащихся в классе и количества заданий – «повторов», которые им распечатаны).

Изучение новой темы.

Для достижения цели уроке используются знания предыдущих уроков, а именно график прямо пропорциональной зависимости. Беседа с учащимися строится таким образом, что в ходе беседы и наводящих вопросов учащиеся сами вместе с учителем обсуждают материл новой темы, приходят к мнению, что графиком прямой пропорциональности является прямая, проходящая через начало координат. Выясняют сколько точек достаточно для построения графика зависимости. Выясняют как располагается график зависимости в зависимости от знака  по координатным четвертям.

Теоретический материал.

Отмечается, график прямой пропорциональности является частным случаем графика зависимости между величинами, если , то зависимость имеет вид . Такую зависимость называют прямой пропорциональностью. Число в формуле  называется коэффициентом пропорциональности.

Определение: Прямой пропорциональностью называется зависимость, заданная формулой вида , где х -  независимая переменная и  - не равное нулю число. Например, , , - прямо пропорциональные зависимости.

График прямой пропорциональности  – прямая, проходящая через начало координат, при  .

Если , то график прямой пропорциональности находится в І и ІІІ координатной четвертях, если , то график находится во ІІ и ІV координатной четвертях.

Работа в группах:

1.      Построить график зависимости . Определить, в каких координатных четвертях расположен график. Сколько точек достаточно для построения графика функции?

2.Постройте график прямой пропорциональности .

Найдите: 1) значение зависимости, соответствующее значению х, равному -3; 2; 4;

2) значение х, которому соответствует значениям зависимости, равным 4; 2; -2.

Оценивание: Учащиеся оценивают друг друга в группе и затем между группами, ответы проверяются учителем или выдаются листочки с правильными ответами.

Закрепление новой темы:

Задания для парной работы:

1.      Дана точка . Постройте график прямой пропорциональности , проходящей через точку . Найдите значение , соответствующее этой прямой. Запишите формулу прямой пропорциональности.

2. Постройте в одной системе координат графики прямой пропорциональностей:

1)  ; 2)  

  3)  4) 5) Рассмотрите их расположение и сделайте вывод. Как меняется угол между графиком прямой пропорциональности и осью ?

Критерии оценивания:

- построен график зависимости;

- вычислено значение ;

- написана формула прямой пропорциональности;

- построены графики заданных зависимостей;

- сделан вывод об их расположении.

Оценивание осуществляется между парами по ответам, которые предложены учителем и висят на нескольких листочках в разных местах кабинета (на боковых стенах и на боковых досках. В результате выполнения этого задания учащиеся получают сведения о том, что угол между осью и графиком прямой пропорциональности увеличивается с увеличением величины .

Задания индивидуального оценивания предусмотрены

для учащихся со средними способностями: №1,

 для учащихся с более высокими способностями - № 2.

Задание для индивидуального выполнения:

1. Составьте формулу прямой пропорциональности, графиком которой является прямая , проходящая через точку . По графику определите:

а) значения функции, соответствующие значениям аргумента -2; 2; 5;

б) значения аргумента,соответствующие значениям функции -4,5; -6; 1,5.

2. На чертежах представлены графики прямой пропорциональности. Определи по ним коэффициенты пропорциональности и запиши формулы. Какие значения может принимать , когда  изменяется в границах: 1) для чертежей а) и б); 2)  для чертежа в)?

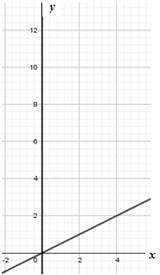
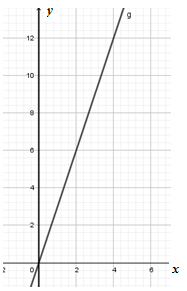
а)                                                                       б)

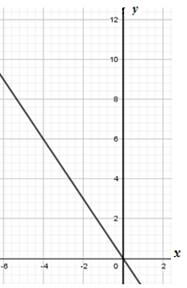
в)

Критерии оценивания:

На доске вывешены правильные ответы, на их основе каждый учащийся проверяет себя сам.

Учитель наблюдает, делает записи о работе всех учащихся.

Провести рефлексию учащихся в конце урока:

- что узнал, чему научился

- что понято не полностью

- над чем еще предстоит поработать

Домашнее задание

1.                 Дана точка  Постройте график прямой пропорциональности , проходящей через точку . Найдите значение , соответствующее этой прямой. Запишите формулу прямой пропорциональности.

2. Постройте в одной системе координат графики прямой пропорциональностей:

1)  ; 2)  

3) ;     4)   . Рассмотрите их расположение и сделайте вывод. Как меняется угол между графиком прямой пропорциональности и осью ?

Более способные ученики смогут выполнить более сложное задание и объяснить решение другим.

Прогресс учащихся будет оцениваться через наблюдение за их работой в течение урока, проверку ответов, чтобы понять есть ли какие-то ошибки.

Учащиеся будут анализировать свою работу с помощью учителя.

Работа в обстановке взаимного доброго отношения, здоровое чувство соперничества и взаимопомощи.

Список полезных ссылок и литературы

1.     Математика. 6 класс. – Т. А. Алдамуратова, Т. С. Байшоланов. – Алматы: «Атамұра», 2011.

2.     Математика. 6 класс. Часть 2. – Г. В. Дорофеев, Л. Г. Петерсон. – Москва: «Ювента», 2010.