Аксиоматическое система исчисления высказываний

Аксиоматическое система исчисления высказываний

 

Табличное построение функций истинности не является единственным способом построения логики высказываний. Существуют и другие способы обоснования истинности тех или иных высказываний. Среди них особо существенно аксиоматическое представление логики высказываний. В чем его суть?

Выбираются некоторые тавтологии логики высказываний и рассматриваются, как такие высказывания, истинность которых дана заранее. При этом не обязательно, что эти высказывания будут очевидны сами по себе. Важно, чтобы они были удобны для получения вывода. Могут быть выбраны в качестве аксиоматических различные высказывания. Число их так же может быть разным. Большее число аксиом иногда облегчает процесс получения вывода. В известной книге Д. Гильберта и В. Аккермана “Основы теоретической логики” в качестве аксиом берутся четыре формулы логики высказываний:

a) a v a ® а

b) а ® a v b

c)a v b ® b v a

d) (а ® b) ® [d v a ® d v b]

Обозначим А и В не отдельные высказывания, которые обозначались а и b, а целые формулы логики высказываний. Например, те, которые выше были приведены в качестве аксиомы. С помощью этих символов можно сформулировать

правила вывода:

а) Правило подстановки. Вместо А (переменного высказывания) везде, где эта буква встречается, можно подставить одну и ту же формулу исчисления высказываний.

b) Схема заключения. Из двух формул А и А ® В получаем новую формулу В.

Формула считается доказуемой, если она или аксиома, или получена из аксиомы с помощьюуказанных правил или же из таких формул, которые уже доказаны.

Аксиоматическое построение именно логики высказываний обладает рядом серьезных преимуществ в сравнении с аксиоматическим построением других разделов логики. Легко доказать, что система аксиом логики высказываний является непротиворечивой, т. е. что с помощью этих аксиом нельзя доказать одновременно а и ¬а. Приведенные аксиомы логики высказываний являются также независимыми друг от друга, т. е. нельзя вывести хотя бы одну из них из других аксиом. И самое интересное, что система аксиом логики высказываний полна в том смысле, что присоединение к этой системе аксиом какой-либо новой аксиомы, которая не выводима из этой системы аксиом, приводит к противоречию.

Для нас наиболее существенно то, что в рамках логики высказываний можно доказать в качестве теорем любую из тех тавтологий, которые мы рассматривали выше, а также все те тавтологии, которые мы не

рассматривали.

В рамках аксиоматического построения логики высказываний имеется большая литература, к которой мы и отсылаем читателя. Для наших целей, т. е. для практического применения логики высказываний к анализу нашего мышления, сказано достаточно.

 

 

Проблемы аксиоматического исчисления высказываний

Теорема. Проблема разрешимости для исчисления высказываний разрешима.

Доказано существование алгоритма, который позволяет для любой заданной формулы исчисления высказываний определить, является ли она доказуемой или не является.

Определение. Логическое исчисление называется непротиворечивым, если в нем не доказуемы никакие две формулы, из которых одна является отрицанием другой.

Определение. Аксиоматическое исчисление называется непротиворечивым, если в нем не существует такая формула A, что доказуема A и доказуема , в противном случае (если такая формула существует), исчисление противоречиво.

Теорема. Исчисление высказываний непротиворечиво.

Определение. Аксиоматическое исчисление называется полным в узком смысле, если добавление к списку его аксиом любой недоказуемой в исчислении формулы в качестве новой аксиомы приводит к противоречивому исчислению.

Определение. Исчисление высказываний называется полным в широком смысле, если любая тавтология в нем доказуема.

Теорема. Исчисление высказываний полно в узком смысле.

Теорема. Исчисление высказываний полно в широком смысле.

Определение. Аксиома A называется независимой от всех остальных аксиом, если она не может быть выведена из остальных аксиом.

Определение. Система аксиом исчисления называется независимой, если каждая аксиома системы независима.

Теорема. Система аксиом исчисления высказываний независима.

 

Определение логического следствия

Если Q - тавтология, то ее обозначают как ъ= Q. Если E – множество формул, то запись E ъ= Q означает, что при всех интерпретациях, при которых истинны все формулы из E, истинна также формула Q. Формула Q называется логическим следствием из E. Таким образом, тавтология – логическое следствие из пустого множества.

Если E содержит единственный элемент P, то P ъ= Q. Тогда Q является логическим следствием P тогда и только тогда, когда импликация P ® Q есть тавтология, или P ъ= Q « ъ= (P® Q).

В более общем виде, можно написать:

{ F₁, F₂,…, F_n }ъ= Q « ъ= (F₁ Щ F₂ Щ…F_n) →ъъ= Q.

Выявление того факта, что из множества высказываний (формул исчисления) логически следует некоторое другое высказывание (формула) и является, по существу, одной из основных задач исчисления.

Определение 5: Пусть даны формулы F₁, F₂,…, F_n и формула Q. Говорят, что Q есть логическое следствие формул F₁, F₂,…, F_n тогда и только тогда, когда для всякой интерпретации I, в которой F₁ Щ F₂ Щ…F_n истинна, Q также истинна. F₁, F₂,…, F_n называются аксиомами (или постулатами, или посылками, или гипотезами).

Если формулы P и Q – логические следствия друг друга, то они называются логически эквивалентными. Такая ситуация имеет место тогда и только тогда, когда формула (P « Q) является тавтологией.

 

Понятие тавтологии совпадает с понятием теоремы в аксиоматической системе. Аксиоматическая система обладает свойством адекватности, то есть она состоит из множества аксиом, считающихся тавтологиями. Кроме аксиом в аксиоматическую систему входит множество правил вывода, позволяющих строить новые тавтологии из аксиом и уже полученных тавтологий. Выводимая формула обозначается ъ--P.

Исчисление высказываний тоже является аксиоматической системой. Любая аксиоматическая система должна удовлетворять следующим требованиям:

1. Непротиворечивость: невозможность вывода отрицания уже доказанного выражения (которое считается общезначимым);

2. Независимость (минимальность): система не должна содержать бесполезных аксиом и правил вывода. Некоторое выражение независимо от аксиоматической системы, если его нельзя вывести с помощью этой системы. В минимальной системе каждая аксиома независима от остальной системы, то есть, не выводима из других аксиом.

3. Полнота (взаимность адекватности): любая тавтология выводима из системы аксиом. В адекватной системе аксиом любая выводимая формула есть тавтология, то есть верно, что ъ-- P® ъ= P. Соответственно в полной систем верно: ъ= P® ъ--P.

Некоторое множество тавтологий составляет систему аксиом A. Приведем две наиболее известные системы аксиом, обладающие всеми вышеперечисленными свойствами.

Классическая система аксиом:

1. P ®(Q ® P);

2. (P ®(Q ® R))®((P ® Q)®(P ® R));

3. (ШP ® Ш Q) ® ((ШP ® Q) ® P).

Система аксиом Новикова:

1. P ®(Q ® P);

2. (P ®(Q ®R))®((P ® Q)®(P ® R));

3. P Щ Q ® P;

4. P Щ Q ® Q;

5. (P ® Q) ®((P ® R) ®(P ® Q Щ R));

6. P ® P Ъ Q;

7. Q ® P Ъ Q;

8. (P ® R) ®((Q ® R) ®(P Ъ Q ® R));

9. (P ® Q) ®(Ш Q ®Ш P);

10. P ®ШШ P;

11. ШШ P ® P.

 

 

 

ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ

Построение и анализ логических исчислений (высказываний и предикатов) составляют содержание одного из наиболее важных разделов современной логики как науки. Это – существенная часть теории дедукции. Теория дедукции включает: 1) описание формализованного языка; 2) логику языка; 3) исчисление.

Исчисление – это формализация соответствующей логики. Исчисления составляют основное содержание современной логики. Теория дедукции, включающая логические исчисления,– это формальная логика в строгом смысле этого слова. Однако в данном случае речь идет о современном этапе логики. Как в традиционной, так и в современной логике предметом изучения формальной логики (теории дедукции) являются формы правильных рассуждений (выводов, доказательств), или, как их было принято называть прежде, формы дедуктивных умозаключений.

Умозаключением вообще называют один из приемов познания – выведение из имеющихся высказываний нового высказывания, то есть некоторый логический прием получения нового знания на основе имеющегося.

Наряду с дедуктивными выводами (умозаключениями) существуют также индуктивные (а некоторые авторы выделяют еще и традуктивные выводы).

Специфика дедуктивных выводов состоит в том, что они обеспечивают истинность выводимого высказывания – заключения – при истинности исходных суждений – посылок вывода (умозаключения). Это свойство дедуктивных выводов обусловлено, в свою очередь, наличием определенной связи между их посылками и заключением. Их связь воспроизводит отношения логического следования между соответствующими высказываниями.

Имеется принципиальное различие между теорией дедукции в традиционной логике и современной. В традиционной логике теория сводилась, в основном, лишь к эмпирическому выделению и описанию некоторых форм правильных рассуждений – правил дедуктивного вывода – без какого-либо полного их обоснования. Дело в том, что в прежней логике не было необходимых для этой цели понятий логического закона и отношения логического следования.

Основой метода построения теории дедукции с применением метода логических исчислений является, как мы увидим позднее, наличие взаимосвязей между самими законами и правилами вывода, в силу которых одни законы и правила можно обосновывать с помощью других. Исчисление (логическое) – это теория, которая строится, как уже ясно из предыдущего, на базе некоторого формализованного языка, например, исчисление высказываний на базе описанного языка логики высказываний. При построении исчисления, во-первых, в качестве исходных выделяется минимальное множество формул – законов логики – и правил вывода (в аксиоматических системах) или только правил (в натуральных системах). Во-вторых, определяются понятия вывода и доказательства. Понятие вывода – какой-либо формулы из множества формул – и понятие доказательства формулы являются основными в логическом исчислении. Эти понятия определяются таким образом, чтобы а) всякая доказуемая формула представляла собой закон логики, формулируемый в данном языке, и чтобы б) была возможность осуществить доказательство любой формулы, представляющей собой закон логики. При этом в случае доказательства формул вида  осуществим также вывод формулы В из множества формул A₁, A₂, ..., А_n, соответствующий имеющемуся в таком случае отношению логического следования: A₁, A₂, ..., А_n ╞ В. Показательно, что выводы и доказательства осуществляются при этом по формальным правилам, то есть по таким правилам, для применения которых не требуется учитывать смысл употребляемых высказываний, надо учитывать лишь характер знаковых форм этих высказываний (состав и порядок расположения знаков языка, из которого они построены). Более того, правильность или неправильность осуществляемых выводов и доказательств оценивается без учета смысла имеющихся высказываний. Последний может приниматься во внимание лишь в эвристических целях – при поиске и составлении плана доказательства или вывода, при определении необходимых средств его построения и т.д.

Все сказанное означает, что в исчислении осуществляется формализация основных понятий логики, а именно: закона логики и отношения логического следования. Для каждого из этих семантических понятий формулируется его синтаксический (формальный) аналог: для закона логики – доказуемая формула, для отношения логического следования – формальный вывод, в результате осуществления которого устанавливается формальная выводимость. Употребляя для доказанности формулыА обозначение ├ А, а для выводимости формулы В из некоторого множества формул Г обозначение Г ├ В, получаем – при правильном построении исчисления – следующие соотношения между указанными семантическими понятиями и их синтаксическими аналогами:

 

├ А е. т. е. ╞ А и Г ├ В е. т. е. Г ╞ В.

 

Если выполняются эти соотношения, то говорят, что в исчислении осуществлена адекватная формализация основных понятий: закона логики и отношения логического следования. Важно заметить, что, в силу сказанного, построение логического исчисления означает также формализацию рассуждений. Естественные рассуждения заменяются здесь формальными преобразованиями знаковых форм высказываний. Это обеспечивает точность и проверяемость выводов и доказательств и открывает возможность передачи осуществления соответствующих видов интеллектуальной деятельности человека машине. Однако в тех или иных случаях оказывается, что формализация неполна, а для некоторых языков она и в принципе не может быть полной. При неполной формализации имеем: если ├ А, то ╞ А, но обратное имеет место не для любых формул. Аналогично, при наличии выводимости Г ├ В имеется отношение Г ╞ В, но не для всякого отношения логического следования может быть построен формальный вывод, то есть получена соответствующая формальная выводимость. В последнем случае говорят, что логическое исчисление непротиворечиво относительно заданной семантики языка, но не является полным. При адекватной же формализации основных семантических понятий оно семантически непротиворечиво и полно относительно заданной семантики. Утверждения о наличии у исчисления этих и других подобных свойств называются метатеоремами исчисления. Их доказательство осуществляется иными средствами, чем доказательство теорем самого исчисления (Важную роль здесь играет метод математической индукции.).

Существуют различные способы формализации логики и соответственно различные формы (или типы) логических исчислений. В качестве основных выделяются аксиоматические системы, натуральные системы и системы секвенциального типа. Внутри каждого типа возможны также различные, но эквивалентные между собой (представляющие формализацию одной и той же содержательной логической теории) системы, различающиеся составом постулатов (аксиом и исходных правил вывода – в аксиоматических системах; исходных правил вывода – в натуральных системах; исходных секвенций и правил вывода для секвенций – в исчислениях секвенций).

Построение систем логических исчислений имеет двоякое значение. Во-первых, теоретическое для самой логики, поскольку в процессе и в результате этого построения выявляются связи между логическими законами, правилами вывода. Из бесконечного множества тех и других выделяется множество исходных, достаточных для доказательства всех формул, представляющих логические законы, для воспроизведения всех возможных отношений следования, для обоснования любого из допустимых правил рассуждения и т.п. Во-вторых, построенное логическое исчисление может быть использовано как логический аппарат для осуществления выводов и доказательств в тех или иных нелогических теориях, построенных на базе соответствующего прикладного формализованного языка. Построение теории при этом осуществляется просто добавлением специальных ее аксиом к постулатам логического исчисления.

 

 

При построении аксиоматических исчислений качественно различаются системы с конечным и бесконечным множеством аксиом, или – системы с аксиомами и системы со схемами аксиом. Бесконечное множество аксиом задается перечислением некоторого конечного множества схем аксиом.

 

 

III. Доказательством некоторой формулы В в данной системе называется непустая конечная последовательность формул B₁, B₂,.... В_т, в которой каждая формула есть или аксиома (частный случай какой-либо из схем аксиом) или получается из предыдущих формул последовательности по правилу вывода и последняя формула В_ткоторой есть В.

Формула, для которой имеется доказательство, называется теоремой системы.

Нетрудно проверить, что последовательность, состоящая из одной аксиомы, есть доказательство этой аксиомы. Значит, все аксиомы системы являются и ее теоремами.

В практике познания в определенных случаях возникает необходимость проводит рассуждения с использованием некоторых допущений, то есть высказываний, которые не являются доказанными, например, в той или иной теории (Ничто не мешает нам, конечно, рассматривать в качестве допущения и некоторую формулу, фактически являющуюся теоремой, отвлекаясь от того, что существует ее доказательство.). Формальным аналогом таких рассуждений у нас будет понятие вывода из допущений.

Выводом формулы В из множества допущений Г называется непустая конечная последовательность формул B₁, B₂,.... В_т, в которой каждая формула есть или некоторое допущение из Г, или аксиома системы, или получается из предыдущих формул по правилу вывода, и последняя формула В_т этой последовательности есть В.

Очевидно, что понятие вывода из допущений является обобщением понятия доказательства. Доказательство есть вывод из пустого множества допущений. Утверждение о наличии вывода (выводимости) формулы В из множества допущений Г записывается (в метаязыке, конечно) в виде Г ├ В; в случае пустого Г (то есть при наличии доказательства В) имеем ├ В (читается: «В доказано» или «В есть теорема системы»).

Рассмотрим в качестве примера доказательство формулы  Для удобства нумеруем члены последовательности и указываем для каждой формулы, является ли она аксиомой или получена из других формул; указания такого рода называются анализом доказательства (вывода).

 

 

Итак, имеем  есть теорема нашей системы».

Если вместо формул (выражений языка) использовать схемы формул (выражения метаязыка), а вместо аксиом – схемы аксиом и их варианты, то получим схему доказательства формул определенной структуры. Соответственно вместо выводов можем строить схемы выводов. Каждый вариант той или иной из схем аксиом мы обозначаем тем же названием.

Схема доказательства формул вида  (Ясно, конечно, что к формулам данного вида будут принадлежать такие, например, как: и др.).

 

 

В символической логике имеется доказательство того, что приведенная формулировка исчисления высказываний представляет собой адекватную формализацию понятий закона логики и отношения логического следования.

Мы не останавливаемся здесь подробно на рассмотрении этой системы, как и вообще аксиоматических построений, поскольку имеются значительные сложности в применении их как аппарата дедукции. Уже из рассмотренного примера доказательства казалось бы самого простейшего закона логики видно, насколько трудно осуществимы в этой системе доказательства и выводы. Трудно определить в каждом конкретном случае доказательства, какие именно из аксиом нужно выбрать в качестве посылок для его осуществления. К тому же выводы здесь значительно отличаются от тех, которые мы имеем в естественном языке. И отличаются именно тем, что в последних не употребляются в качестве частей – посылок выводов и доказательств – законы логики, а ведь аксиомы, как мы помним, и являются таковыми. В математических доказательствах, например, в геометрии, посылками доказательств являются аксиомы геометрии или уже доказанные на их основе утверждения. В ряде других случаев, и особенно вне аксиоматических теорий, это могут быть просто какие-то допущения (гипотезы). Указанные трудности в построении выводов и доказательств и несоответствие естественным рассуждениям преодолеваются в определенной мере в системах натурального типа, к рассмотрению которых мы и переходим; там мы увидим, в частности, что доказательство того же закона тождества  мы получим всего в два шага! Однако в натуральных системах возникают свои трудности. Они связаны с определением вывода. Обычно его определения получаются здесь весьма усложненными. Дело в том, что, устраняя из множеств возможных посылок выводов и доказательств законы логики, мы должны использовать так называемые непрямые правила рассуждения (см. дальше). В силу этого опять-таки происходит отдаление способов построения выводов в этих исчислениях от естественных рассуждений. Мы же даем здесь систему, которая максимально приближена к естественным рассуждениям.

НАТУРАЛЬНАЯ СИСТЕМА ИСЧИСЛЕНИЯ ВЫСКАЗЫВАНИЙ

Постулатами натуральной системы являются только правила вывода. В выводах и доказательствах в качестве посылок используются только допущения. К их числу можно относить, конечно, и специальные аксиомы теорий, отличая их при этом от таких допущений, которые играют в доказательствах промежуточную роль и, в конечном счете, исключаются из доказательств. Более того, всякий вывод (и в частности, доказательство) начинается с некоторых допущений.

Мы будем строить выводы, учитывая зависимость получаемых в них на каждом шаге результатов – формул вывода – от введенных допущений. Указания на эту зависимость будут называться характеристиками зависимости формул вывода от допущений. Каждый шаг вывода, представляющий собой некоторую формулу этого вывода с характеристикой зависимости, будет иметь вид: А [Г], где А – сама формула вывода, а Г – множество формул, от которых зависит А в этом выводе. Г – может быть, конечно, и пустым множеством. Этот случай будет указывать, что формула является законом логики и вместе с этим – теоремой логического исчисления.

Понятие зависимости формул определяется индуктивно:

1. Каждое допущение вывода зависит от самого себя. Это означает, что характеристикой зависимости допущения А является одноэлементное множество {А}, однако фигурные скобки мы далее будем опускать и будем употреблять обозначение А [А].

2. Для остальных формул вывода, получаемых по правилам вывода из других, зависимости определяются в самих формулировках правил.

Правила вывода. Мы будем рассматривать систему, включающую в качестве постулатов правила вывода (исходные правила) относительно всех ранее выделенных в языке логики высказываний логических констант (связок): конъюнкции – &, дизъюнкции – v, импликации –  и отрицания  Как обычно в натуральных системах, для каждой логической константы имеется правило введения этой константы и правило удаления ее (этим объясняются специальные обозначения правил, например, «&_В» – правило введения конъюнкции;  – первое и второе правило исключения конъюнкции; А, В, С – далее любые формулы; Г, Δ – любые, возможно пустые, множества допущений. В правилах мы различаем также посылки применения данного правила с характеристиками зависимости (записываются над чертой) и заключения применения данного правила,– формула с характеристикой зависимости (указывают под чертой). Посылки – уже имеющиеся в выводе формулы, а заключение – формула, которую согласно правилу мы имеем право добавлять (и добавляем при применении правила) к имеющемуся выводу. Итак, мы принимаем следующую систему правил:

 

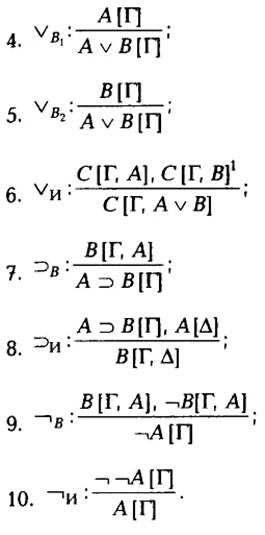
¹По данной формулировке это правило выглядит как введение дизъюнкции. В каком смысле оно является исключением дизъюнкции, будет разъяснено позже.

 

Вместо правила v_и может быть взято прямое правило 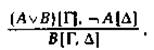 Это известная форма вывода, называемая modus tollendo ponens разделительного силлогизма 

 

Для завершения описания исчисления необходимо сформулировать понятие вывода и доказательства.

Выводом некоторой формулы В из множества допущений Δ называется непустая конечная последовательность формул с характеристиками зависимости B₁[Г₁], ... ,В_n[Г_n], в которой каждая формула есть либо допущение, либо поручена из предыдущих по какому-либо правилу вывода, причем В_n есть В (заключение вывода), а Г_n – некоторое множество допущений Г, являющееся подмножеством  Ясно, что данную последовательность можно охарактеризовать также как вывод В из Г. Характеризуя же его как вывод из Δ, мы подчеркиваем то обстоятельство, что каждый вывод формулы В с характеристикой Г, представляет бесконечное множество выводимостей, поскольку Δ может быть любым расширением Г. Выводимость Г ├ В является для данного вывода наиболее сильной, так как в выводе использованы все допущения из данного множества Г (хотя возможен и другой вывод с меньшим числом использованных допущений).

Данная система исчисления эквивалентна рассмотренной выше аксиоматической формулировке исчисления высказываний. Это значит, что формализация следования здесь адекватна, то есть каждому случаю отношения следования Г ╞ A в системе соответствует отношение формальной выводимости Г ├ А и наоборот. Поскольку согласно определению следования «Если В следует из Г, то оно следует из любого расширения Г», постольку аналогичное свойство имеет и отношение формальной выводимости (если Г ├ В, то и Δ ├ В, где Δ – любое расширение Г, то есть ).

Итак, вывод с заключением В, зависящим от множества допущений Г – при непустом Г – мы будем обычно характеризовать как Г ├ В. В случае если Г пусто, вывод называется доказательством формулы В и характеризуется как ├ В (вывод В из пустого множества допущений). Но и в этом случае любое доказательство В представляет собой также вывод Δ ├ В, при любом Δ. Очевидно, что в силу указанного понятия выводимости правомерно правило: 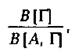 допускающее возможность расширения характеристик зависимости. Это правило, называемое часто правилом утончения и являющееся производным, мы будем применять наряду с указанными выше основными правилами (как будет показано дальше, его применение может быть исключено за счет более сильной формулировки правил  Формально – как производное правило – оно может быть получено из основных правил системы.) В самом деле, положим, что в каком-то выводе получено заключение В с характеристикой зависимости Г, то есть имеем В [Г]. Тогда мы можем продолжить этот вывод, добавив допущение А, то есть А [А] и получить (по правилу &_B) A & В [A, Г], а отсюда (по правилу  – В [А, Г]. Итак, имея в выводе В [Г], мы по основным правилам системы получили В [А, Г].

Рассмотрим теперь несколько примеров выводов и доказательств. Допущения будем выделять знаком «+». Как и обещали, приведем доказательство закона тождества.

 

 

В дальнейшем, как и в приведенном примере, будем нумеровать все формулы вывода и для упрощения записей вместо формул в характеристиках зависимости будем указывать их номера в выводе.

 

 

Решение вопроса о том, какие вспомогательные допущения использовать для построения того или иного вывода, относится к числу творческих моментов. При данном построении системы (с характеристиками зависимости) в вывод могут вводиться, вообще говоря, любые допущения, они просто не найдут отражения в характеристиках зависимости. Любое допущение может использоваться независимо от того, применялись ли правила, исключающие его. Однако при введении вспомогательных допущений существенно иметь в виду возможность устранить в конечном счете зависимость от них подлежащей выведению или доказательству формулы. Это может быть осуществлено только применением правил 

 

 

Упражнения

 

1. Осуществите доказательства, данные в примерах 3 и 4, без применения правила утончения, пользуясь только что введенными формулировками правил 

 

 

Мы уже употребляли такие понятия, как основные правила и производные. Основные – это исходные правила системы (постулаты системы). Производным является правило, заключение которого может быть выведено из его посылок по основным правилам. Мы могли видеть это уже на примере правила утончения. По существу, таким образом, производные правила – это некоторые выводы по основным правилам системы. Они используются в системах для сокращения выводов; применение производного правила есть сокращение именно того вывода, которое оно представляет. Если читатель выполнил предшествующее упражнение 3, то тем самым он получил три производных правила:

 

 

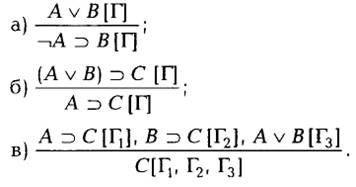
Ясно, что применение производных правил не является обязательным; каждое такое применение может быть заменено соответствующей этому правилу последовательностью формул. Читателю должно быть ясно и то, что каждой доказуемой в системе формуле (теореме) вида  соответствует производное правило 

 

Упражнение

 

1. Доказать теоремы:

 

 

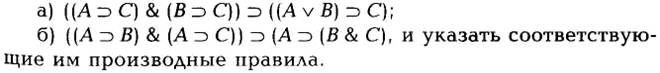
Существенное значение при анализе рассуждений имеет различение прямых и непрямых правил. Прямые правила указывают на выводимость какого-то высказывания из каких-либо высказываний (в исчислении – выводимость формулы из формул). В предлагаемой системе все правила сформулированы как прямые. Однако существенной особенностью обладают правила введения импликации  введения отрицания  и правило исключения дизъюнкции (v_и). В отличие от других они позволяют исключать некоторые допущения из характеристик зависимости формул (возможно с заменой их – как при v_и – другими допущениями), что характерно для непрямых правил рассуждения. При применении «v_и» исключаются допущения А и В с заменой их на A v В; при  исключается допущение А.

В других системах (без характеристик зависимости) они формулируются явным образом как непрямые, соответственно:

 

 

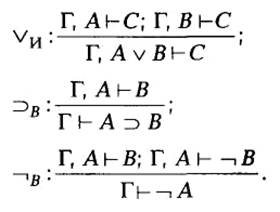
В этой формулировке очевидна их особенность, состоящая в том, что они указывают на возможность заключения о наличии некоторой выводимости на основе других выводимостей. Специфика их в рассуждениях состоит в том, что они дают возможность использовать в рассуждениях наряду с данными посылками вспомогательные допущения с последующим исключением их из рассуждения. Так, желая получить вывод Г, A v В ├ С, мы совершаем «обходной» маневр, используя правило v_и: учитывая указанные в дизъюнкции A v В возможности – истинность А или истинность В – рассуждаем «по случаям (В силу того, что само это правило часто называют правилом рассуждения «по случаям».)» – осуществляем вывод Г, А ├ С, соответствующий случаю истинности А, и вывод Г, В ├ С, соответствующий случаю истинности В. Пользуясь указанным правилом v_и, заключаем после этого о наличии нужной нам выводимости Г, A v В ├ С (здесь содержится обещанное ранее разъяснение, почему именно данное правило называется правилом исключения, а не введения дизъюнкции: дизъюнкция A v B исключается из рассуждения). Например, надо вывести, что «данное число делится на 5» – (С) из дизъюнкции «это число оканчивается на 0 или на 5» – (A v B). С учетом множества аксиом арифметики и выводимых из них утверждений – Г и рассуждая «по случаям», осуществляем сначала вспомогательные выводы Г, А ├ С и Г, В ├ С, затем заключаем о наличии нужной нам выводимости: Г, A v В ├ С.

По правилу  вместо того, чтобы непосредственно выводить условное высказывание  из посылок Г (что обычно представляет определенную сложность), мы заключаем о наличии этой выводимости на основе вспомогательного вывода Г, А ├ В. Из аксиом геометрии Г, например, можно вывести «если углы, полученные при пересечении двух параллельных линий третьей, являются соответственными (А), то они равны (В)» на основании вспомогательного вывода Г, А ├ В.

Правило  в истории логики, как и в конкретных науках, например, в математике, известно как правило опровержения путем «сведения к абсурду».

Часто этот прием опровержения составляет часть другого рассуждения, которое называется «доказательством от противного». Этой форме рассуждения соответствует также непрямое правило: 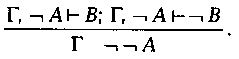Оно может быть получено из предыдущего с использованием правила снятия двойного отрицания обозначенного в нашей системе как  По правилу опровержения имеем 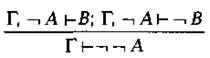 и теперь по правилу  получаем: Г ├ А. Желая доказать, например, что согласно аксиомам геометрии (Г) «из данной точки плоскости, лежащей вне этой плоскости, можно опустить только один перпендикуляр на прямую, принадлежащую этой плоскости», предположим, что это А неверно, то есть имеет место  (можно опустить не один, по крайней мере, два перпендикуляра). Теперь оказывается, что если из точки опущено два перпендикуляра, то сумма углов полученного треугольника больше 180°, поскольку каждый перпендикуляр образует с соответствующей прямой угол, равный 90° (обозначим это утверждение –  оно представляет собой отрицание утверждения В о том, что сумма углов всякого треугольника равна 180°, которое является следствием аксиом геометрии, а значит, и расширения множества Г за счет добавления нашего утверждения ). Таким образом, мы имеем две выводимости:  по указанному правилу доказательства «от противного» получаем отсюда: Г ├ А.

В дополнение к уже рассмотренным примерам законов логики приведем список некоторых других наиболее важных схем законов логики (которые читатель может использовать в качестве упражнений для доказательств):

 

 

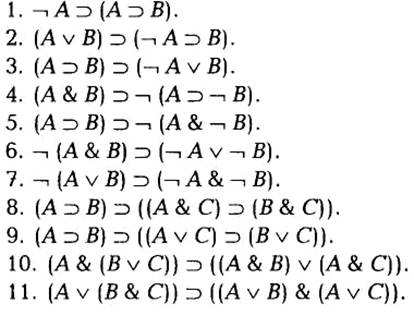
Эти законы, как нетрудно заметить, выражают связь между логическими константами языка логики высказываний.

 

Язык, логика и исчисление предикатов

ЯЗЫК ЛОГИКИ ПРЕДИКАТОВ

Приступая к изучению языка логики предикатов, полезно вспомнить основные особенности языков этого типа (см. § 9). К языку логики предикатов (сокращенно – ЯЛП) мы переходим от языка логики высказываний, устраняя те недостатки последнего, которые были связаны с лежащим в его основе абстракциями относительно пропозициональных переменных. В ЯЛП явно должны быть представляемы субъектно-предикатные структуры высказываний, от которых происходило отвлечение при введении пропозициональных символов. Выражаемыми должны быть, например, высказывания видов: «а обладает свойством Р», «а и b находятся в отношении Р», «Для всякого предмета из некоторого множества S верно, что он обладает свойством Р», «Для всякого предмета из множества S существует предмет этого множества такой, что эти предметы находятся в отношении R», «Если неверно, что всякие два предмета некоторого множества находятся в отношении R, то существуют по крайней мере два предмета этого множества, не находящиеся в этом отношении», «Если в множестве S существует предмет х, который находится в отношении R с любым предметом уэтого множества, то для всякого предмета у того же множества существует предмет х такой, что последний находится в отношении R к первому» и т.п.

Ясно, во-первых, что для выражения таких утверждений у нас нет средств в языке логики высказываний. Ясно и то, что для выражения подобных высказываний в ЯЛП мы должны иметь в числе его исходных символов общие имена предметов; аналогами последних в ЯЛП будут предметные переменные х, у, z, а также они же с числовыми индексами х₁, х₂, ... и т.д. Потребность в общих именах при употреблений ЯЛП сохранится лишь для описания областей возможных значений этих переменных, что относится уже не к самому языку, а к метаязыку. Нужны также знаки свойств и отношений. Для выражения высказываний вида «Объем тела а больше объема тела b» или «Синус х меньше косинуса y» и т.п. необходимы, конечно, и предметные функторы. Впрочем, перечислим систематически основные типы выражений описываемого языка, каковыми являются: исходные символы, термы и формулы. Описание этих выражений составит синтаксис ЯЛП.

СИНТАКСИС ЯЗЫКА ЛОГИКИ ПРЕДИКАТОВ (ИСХОДНЫЕ СИМВОЛЫ, ТЕРМЫ, ФОРМУЛЫ)

I. Исходные символы языка.

1. Предметные переменные х, у, z, а также х с числовыми индексами:

x₁, x₂, ..., х_n, ... (бесконечное счетное множество).

2. Предметные константы (аналоги собственных имен естественного языка):

а₁, а₂, ..., а_n, ... (также бесконечное счетное множество).

3. Знаки свойств и отношений различных местностей – предикатные символы, или предикаторы:

 

 

(верхние индексы указывают на местность предикатора, нижние индексы используются для расширения множества предикаторов той или иной местности; количество предикатных символов той или иной местности вводится в зависимости от предназначения языка. Однако, поскольку речь идет о языке логики предикатов, должен быть введен по крайней мере один предикатный символ).

4. Знаки предметных функций различных местностей (предметные функторы):

f¹₁, f¹₂, …

f²₁, f²₂, …

…………

f^k₁, f^k₂, …

 

(число функциональных символов той или иной местности зависит также от предназначения языка, возможно отсутствие символов этого рода вообще).

5. Логические константы:  – соответственно – импликация, конъюнкция, дизъюнкция, отрицание, квантор общности и квантор существования. (Зачастую вводят лишь некоторые из этих символов. Из кванторов достаточны только  из остальных, называемых логическими связками, достаточно  Другие константы, как, впрочем, и другие знаки, могут вводиться по определению.)

6. Технические знаки: ( – левая скобка, ) – правая скобка, ,– запятая.

Предметные константы, предикаторы, предметные функторы и предметные переменные называют дескриптивными терминами языка, при этом три первых категории (в отличие от предметных переменных) суть – дескриптивные постоянные данного языка.

II. Термы. Выражения этого типа являются аналогами имен естественного языка.

Определение: а) любая предметная переменная и предметная константа есть терм; б) если t₁, t₂, ..., t_n есть термы и fⁿ_i есть n-местный предметный функтор, то fⁿ_i (t₁,t₂, ..., t_n есть терм; в) ничто, кроме указанного в пунктах а) и б), не есть терм.

III. Формулы. В числе этих выражений имеются аналоги повествовательных предложений естественного языка, а также высказывательные формы – предакаты, представляющие собой особую семантическую категорию, которая не выделяется – по крайней мере явным образом – в естественном языке.

Определение: а) если t₁, t₂, ..., t_n термы и Рⁿ_i n-местный предикатор, то Рⁿ_i (t₁, t₂, ..., t_n) есть формула (атомарная); б) если А и В – формулы, то  – формулы; в) если х есть предметная переменная и А – формула,  – формулы; г) ничто, кроме указанного в пунктах а) – в), не есть формула.

Договоримся в дальнейшем опускать, когда это удобно, внешние скобки в отдельно взятых формулах; например, вместо (А & В) писать просто А & В.

Использованные в определениях терма и формулы символы t₁, t₂, ..., t_n и fⁿ_i, Pⁿ_i, А, В, х (и в дальнейшем возможно x₁, х₂ и т.д.) – знаки метаязыка называемые также синтаксическими переменными, возможными значениями которых являются выражения соответствующей категории описываемого (объектного) языка.

Формулы А и В, встречающиеся в пунктах б) и в), называются подформулами указанных здесь формул.

Введенные понятия исходного символа, терма и формулы языка являются эффективными (иначе: рекурсивными). Последнее означает, что имеется точный способ, с помощью которого всегда можно определить, относится ли некоторый символ к числу исходных символов языка, а для каждой последовательности исходных символов можем определить, представляет ли она терм или формулу. Для термов и формул такой способ заключен в их индуктивных определениях. Так, в каждой формуле, содержащей логические константы (знаки логических операций), имеется главная, или, что то же, последняя, в построении формулы операции. Выделив ее, мы выделяем тем самым собственные подформулы этой формулы. В последних снова выделяем главную операцию и так далее, пока не дойдем до какой-либо атомарной формулы. Если в процессе такого анализа исходного выражения в какой-либо части его, не являющейся атомарной формулой, нельзя выделить знак главной операции, то эта часть не является формулой, а следовательно, таковой не является все выражение. Возможность распознавания атомарных формул среди последовательностей символов является очевидной. (При констатации эффективности введенных понятий подразумевается так называемая абстракция отождествления, согласно которой все различные случаи употребления некоторого символа, например а, рассматриваются как различные экземпляры одного и того же символа, и предполагается, что мы умеем узнавать символ, несмотря на некоторые, всегда имеющиеся различия в его написаниях.)

 

Упражнения

 

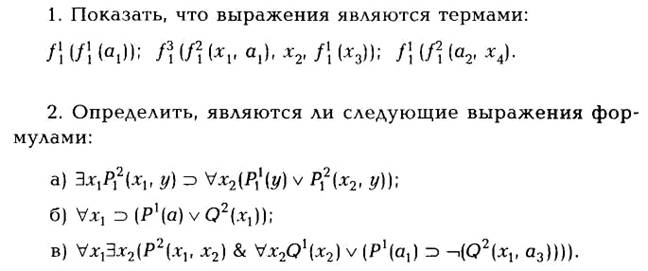
СВОБОДНЫЕ И СВЯЗАННЫЕ ВХОЖДЕНИЯ ПЕРЕМЕНЫХ В ФОРМУЛЫ

Каждый случай, когда в последовательности знаков, представляющей собой формулу А, встречается предметная переменная х, называется вхождением этой переменной; каждое вхождение в формулу А предметной переменной х в часть вида  называется связанным. Подформула В формул указанного вида называется областью действия соответственно квантора общности  и квантора существования  с переменной х. Связанным является вхождение переменной, стоящей непосредственно за квантором, и каждое вхождение ее в область действия квантора. Всякое вхождение х в отличие от указанного, называется свободным. Переменная х, имеющая связанные вхождения в формулу A, называется связанной в этой формуле; переменная, имеющая свободные вхождения в формулу А, называется свободной в этой формуле.

Обратим внимание на то, что согласно определению свободной и связанной переменной одна и та же переменная в одной и той же формуле может быть свободной и связанной. Такова, например, переменная x₁ в формуле  переменная х₂ является здесь свободной, но не связанной. Мы рассматриваем здесь только такие термы, в которых все переменные могут иметь лишь свободные вхождения и, значит, являются свободными переменными. Формула и терм, не содержащие свободных переменных, называются соответственно замкнутой формулой и замкнутым термом (очевидно, что для рассматриваемых здесь термов, если терм замкнут, то он вообще не содержит переменных).

 

Упражнения

 

1. Указать, связанные и свободные вхождения переменных в следующие формулы:

 

 

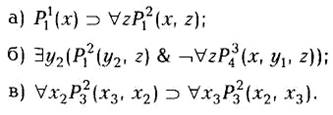
2. Укажите, какие переменные в формулах упр. 1 являются свободными и какие связанными в них.

СЕМАНТИКА ЯЗЫКА ЛОГИКИ ПРЕДИКАТОВ

Семантику языка, как мы видели при анализе естественного языка, составляет совокупность предметных значений и смысловых содержаний его выражений. Но в данном случае, поскольку речь идет не об анализе уже имеющегося языка, а о построении – в данном случае логического формализованного языка – то семантикой называют совокупность правил приписывания значений выражениям этого языка. Точнее говоря, здесь даже не ставится задача построения какого-то определенного языка. Создается лишь некоторая схема языка определенного типа, в данном случае языка так называемой классической логики предикатов первого порядка. Этот тип языка отличается от языков других типов, даже языков с тем же синтаксисом (например, языка интуиционистской логики предикатов, определенной системы релевантной логики) своей семантикой. Приписывание значений отдельным выражениям языка, составляющим дескриптивным терминам, употребляемым при построении формул, осуществляется лишь в составе тех или иных формул и при этом различно от случая к случаю в зависимости от характера решаемых логических задач, (например, при переводе каких то высказываний с естественного языка на данный формализованный, при анализе логических отношений между формулами данного языка, при аксиоматизации некоторых теорий, а именно при формулировке их аксиом в языке данного типа). Совокупность всех правил приписывания значений выражениям языка разбивается на следующие три группы (I, II, III).

I. Правила определения (задания) возможных значений предметных переменных и правила приписывания предметных значений дескриптивным постоянным в составе рассматриваемых в том или ином случае формул – интерпретация выражений языка. II. Правила приписывания значений свободным переменным в составе тех или иных рассматриваемых формулу. III. Правила приписывания истинностных значений интерпретированным формулам, не содержащим свободных переменных.

I. Интерпретация состоит, во-первых, в выборе некоторого непустого множества D индивидов, предметов того или иного типа, к которым могут относиться образуемые из тех или иных формул языка высказывания. Индивиды – любые предметы в широком смысле этого слова, структура которых не учитывается и которые можно отличать друг от друга. В качестве такой области D можно взять множество людей, растений, городов, чисел и т.д.; возможно также объединение в одной области множеств различных предметов, например, людей, городов, домов (положим, для выражения высказываний о местах жительства людей). Но при этом все различные предметы рассматриваются именно как индивиды (Здесь имеются в виду так называемые односортные языки, в которых все переменные – в нашем случае все предметные переменные – имеют одну и ту же область значений. В принципе можно употреблять языки с несколькими сортами переменных, различающимися областями значений, однако всегда можно объединить эти области в одно множество, отражая принадлежность тех или иных предметов, о которых речь идет в некотором высказывании, к той или иной области в самих записях высказываний; напоминаем, что эта возможность была разъяснена при общей характеристике ЯЛП.). Область D – это область возможных значений предметных переменных символы предметных переменных х, у, z, становятся именно переменными лишь при указании области их возможных значений.

Предполагается, что на области D определено некоторое множество свойств, отношений и характеристик предметно-функционального типа (то есть возможных значений предикаторов и предметных функторов).

Второй момент интерпретации языка состоит в задании некоторой функции φ (интерпретационная функция) приписывания значений дескриптивным постоянным (предметным константам, предикаторам, предметным функторам опять-таки в составе рассматриваемых формул). Задание φ в каждом конкретном случае представляет собой просто указание на то, какие значения должны быть приписаны упомянутым исходным символам языка в составе рассматриваемых формул. При этом предметным константам (простые постоянные термы) приписываются в качестве предметных значений определенные предметы из заданной области D. Предикатному (л-местному) символу Рⁿ_i при n = 1 в качестве значения приписываются некоторые свойства а при n > 1 – n-местное отношение (между предметами В (Имея в виду языки экстенсионального типа, каковым является описываемый здесь язык классической логики предикатов, свойства и отношения отождествляются – ради достижения максимальной точности в описании семантики – с их объемами. Так, свойство рассматривается как множество предметов – некоторое подмножество предметной области. Отношение местности, равной n (n-местное отношение), n ≥ 2 – трактуется как множество последовательностей из n предметов (n-ок предметов). Однако мы здесь не прибегаем к такого рода отождествлениям, предполагая, что читателю ясно, что такое свойство и отношение (хотя бы из предшествующего анализа естественного языка).)). Например, если область D есть множество целых положительных чисел, то предикатному символу P¹₁ можно приписать в качестве значения свойство «четно», а предакатору Р₁² отношение «больше» или «меньше». Предметному функтору fⁿ₁ в качестве предметного значения функция φ приписывает какую-нибудь n-местную предметную функцию, определенную на области D. Например, для области чисел таковыми могут быть синус, косинус (одноместные функции), сумма, произведение (двухместные функции), для области людей – одноместные (возраст, рост), для области материальных тел – объем, удельный вес.

Значения сложных термов, каковыми являются также предметы из области D, и приписывание которых составляет их интерпретацию, вычисляются в зависимости от приписанных уже значений их простым составляющим – предметным константам, предметным функторам, а также и возможным предметным переменным, значения которых приписываются по правилам II). Вычисление происходит в соответствии с правилами построения сложного терма. Сложные термы образуются, как мы видели, с применением предметных функторов и строятся индуктивно. Значение такого терма вычисляется последовательно в соответствии с порядком его построения.

Пример. Имеем терм f²₁ (f²₁ (a₁, a₂), f²₂ (a₁, a₃)).

Пусть область D – целые положительные числа, а₁ есть число 3, а₂ = 4, а₃ = 5, f²₁ – сумма, f²₂ – произведение.

Тогда

f²₁ (а₁, а₂) = 7;

f²₂ (а₁, а₃) = 15;

f²₁ (f²₁ (а₁, а₂), f²₂ (а₁, а₃)) = 22.

 

II. Свободным переменным в той или иной формуле (а тем самым и в составе термов этой формулы) в качестве значений приписывают, также как и постоянным термам, предметы из области D. Такие приписывания осуществляются когда мы хотим получить из интерпретированной формулы со свободными переменными высказывание нашего языка. Приписывание осуществляют заменой каждого вхождения некоторой свободной переменной какой-либо предметной константой с одновременной интерпретацией таковой, если она еще не была интерпретирована в формуле.

Будем говорить, что при осуществлении этих приписываний в добавление к уже имеющейся интерпретации формулы, формула оказывается полностью интерпретированной.

Однако важно заметить, что формулы со свободными переменными нужны не только для образования высказываний из них. Они представляют собой особые высказывательные формы, называемые предикатами. Это сложные знаковые формы возможных свойств предметов заданной области и возможных отношений среди этих предметов. По типу их предметных значений они должны быть отнесены к категории предакаторов. Можно назвать их сложными предикаторами (в отличие от простых, указанных среди исходных символов). Надо отметить, что эти формы не выделяются и даже не замечаются в естественных языках. Они играют, однако, решающую роль в теории понятия (см. гл. IV, V). Имея тот или иной предикат, можно ставить вопрос, для каких предметов, которые могут представлять свободные переменные, этот предикат выполняется или не выполняется. В таком случае мы просто указываем предметы для соответствующих переменных (не осуществляя указанных подстановок предметных констант вместо них). Например, можно сказать, что предикат  – выражающий свойство какого-то числа х из области натуральных чисел, состоящее в том, что «если это число больше 5 (знаками отношения «больше» и «5» является соответственно Р² и a₁, то оно делится без остатка (Q²) на некоторое число y», выполняется для чисел 6, 8, 9 и т.д., но не выполняется для 7, 11 и др.

III. Приписывание истинностных значений полностью интерпретированным формулам.

Напомним, что полностью интерпретированная формула – это формула, в которой осуществлена интерпретация дескриптивных постоянных и приписано значение всем свободным переменным, если таковые имеются в ней. Каждая такая формула представляет собой определенное высказывание – с определенным смыслом и истинностным значением – но лишь при условии, если нам известны значения встречающихся в ней – явным или неявным образом – логических констант, (которые и определяются рассматриваемыми правилами III). Явным образом указываются – в сложных формулах – логические константы, перечисленные в списке исходных символов. Простые (атомарные формулы видов Pⁿ(t₁, ..., t_n), по-видимому, не содержат логических констант. Однако, неявным образом здесь присутствует логическое отношение принадлежности свойства Р некоторому предмету t при n = 1 или о наличии отношения Рⁿ между предметами t₁, ..., t_n из области D.

Определение значений всех логических терминов, как явно обозначенных, так и неявно содержащихся в формулах, осуществляется как раз посредством правил приписывания истинностных значений полностью интерпретированным формулам нашего языка (строго говоря, мы имеем здесь гак называемое неявное определение логических констант, по они достаточны для понимания того, какой именно смысл они придают нашим высказываниям).

Правила эти таковы. Значение простого (атомарного) высказывания Pⁿ(t₁, ..., t_n), n ≥ 1, определяется в зависимости от заданных значений термов t₁, ..., t_n и предикатора Рⁿ. Оно зависит от характера предметов данной предметной области. Положим, имеем формулу: Р² (f¹₁(a₁), f¹₁(a₂)). Предположим, что согласно заданной интерпретации D – множество людей: Р² означает «больше»: f¹₁ «возраст»: а₁ – Петров, а₂ – Сидоров. Вся формула представляет собой высказывание «Возраст Петрова больше, чем возраст Сидорова». Высказывание истинно или ложно в зависимости от того, имеет или не имеет место данное отношение между возрастами Петрова и Сидорова.

Заметим, что в части лексики мы перевели здесь высказывание, полученное из определенной формулы рассматриваемого языка (ЯКЛП), по существу на обычный естественный русский язык. В самом ЯКЛП знаковой формой его является упомянутая формула. Подобные переводы обычно напрашиваются сами собой в силу того, что задание значений отдельных терминов – составляющих формулу – осуществляется посредством выражений естественного языка. Мы говорим «значение Р² – больше, а₁и а₂ – соответственно Сидоров и Петров» и т.п.). Это значит, что приписывание предметных значений выражениям описываемого языка осуществляется методом перевода их в тот или иной естественный язык. Может показаться, что при упомянутых переводах высказываний данного языка на естественный теряется та самая точность их выражений, ради достижения которой как раз и строятся формализованные языки. Однако точность здесь по сравнению с естественными языками достигается не за счет более точною употребления отдельных терминов,– достаточная точность их уже должна быть обеспечена при осуществлении интерпретации выражений формализованного языка – а за счет определенных, стандартных способов построения высказываний и их логических форм. И она именно сохраняется, или точнее сказать, должна сохраняться при указанных переводах.

Для сложных формул имеем, предполагая, что все составляющие их формулы полностью интерпретированы.

Формула вида А & В имеет значение «истина» – при данной интерпретации и приписывании значений свободным переменным – е. т.е. А имеет значение И и В имеет значение И.

 

 

Примеры

 

Определим значение формулы –

 

 

при условии, что область возможных значений переменных D есть множество целых положительных чисел, константам а₁ и а₂ приписаны соответственно числа 2 и 3, свободной переменной у – значение 6; предикатный символ Р² имеет в качестве значения отношения «делится». Ясно, что при указанной интерпретации данная формула выражает определенное высказывание: в переводе на русский язык, «Для всякого целого положительного числа х верно, что если оно делится на 2 и на 3, то оно делится на 6». Ясно, что это высказывание и соответственно наша формула истинны. Рассмотрим формулу  Если D – множество людей, Р² – отец, то она представляет собой высказывание «Для всякого человека х существует человек у такой, что он является отцом первого».

Как уже сказано, полностью интерпретированные формулы языка при учете правил III представляют собой высказывания этого языка, а интерпретированные формулы со свободными переменными – предикаты (знаковые формы сложных свойств и отношений соответствующей области предметов D). Неинтерпретированные формулы, не содержащие свободных переменных,– суть логические формы высказываний, а со свободными переменными – логические формы предикатов. Однако предикаты могут трактоваться и трактуются в процессах выводов и доказательств, а также в определении отношения логическою следования и законов логики как специфические высказывания с какими-то подразумеваемыми значениями переменных, как это делается, например, в записи математических уравнений.

Возможность различных истолкований формул со свободными переменными указывает на существование различных истолкований или, как говорят, различных интерпретаций самих свободных переменных в формулах. Вообще различают три возможных интерпретации свободных переменных в составе формул ЯКЛП.

1) Предикатная интерпретация. Она означает, что свободные переменные в формуле рассматриваются как знаки пустых мест в предикате, на которые могут подставляться имена предметов из заданной области D для образования высказываний из предикатов. 2) Условная интерпретация. 3) Интерпретация всеобщности.

При второй и третьей интерпретации свободных переменных формула, содержащая эти переменные, трактуется как высказывание или логические формы таковых (в зависимости от того, являются они интерпретированными или нет). При условной интерпретации некоторой переменной в нем эта переменная рассматривается как знак какого-то – одного и того же во всех своих вхождениях – предмета из области D. А при интерпретации всеобщности какой-либо переменной она рассматривается как знак любого предметы из области D, но одного и того же во всех своих вхождениях в формулу. Иначе говоря, высказывание со свободными переменными равносильно высказыванию, которое получается из данного посредством связывания всех его свободных переменных, взятых в условной интерпретации, квантором существования, а переменных, рассматриваемых в интерпретации всеобщности, квантором общности. В предыдущем описании семантики мы подразумеваем предикатную интерпретацию свободных переменных. А высказывание, получаемое из предиката,– как результат применения этого предиката к предметам, имена которых подставляются вместо свободных переменных. Однако в дальнейшем, например при анализе понятия следования, формулы со свободными переменными трактуются как высказывания с условной интерпретацией этих переменных.

Подчеркнем еще раз значение интерпретации (совокупность правил I). При наличии правил III, то есть при заданном понимании логических констант, определяющих тип языка, различные интерпретации порождают из заданной синтаксической системы фактически различные языки данного типа (в которых используется каждый раз лишь какая-то часть исходных дескриптивных символов).

В заключение данного раздела, касающегося семантики языка, важно заметить, что хотя правила приписывания значений выражениям языка, составляющих в совокупности эту семантику, ориентированы на приписывание значений в каких-то конкретных случаях, их основное значение состоит в том, что они указывают общие принципы, общие способы превращения формул языка в осмысленные выражения. При таком истолковании указанных правил семантика представляет собой теорию означивания выражений данного языка (которую называют также теорией референции).

 

Упражнения

 

Для каждой из следующих формул укажите какую-нибудь интерпретацию (область D) значение дескриптивных постоянных, а также значения свободных переменных, при которых соответствующие формулы, соответственно, истинны и такие, при которых они ложны:

 

 

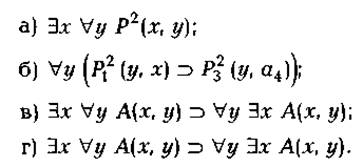
Данные выше разъяснения относительно тех смыслов, которые формулы получают при интерпретации, указывают на принципы перевода высказываний языка логики предикатов на естественный язык. Однако в них можно усмотреть решение и обратной задачи – перевод с естественного на язык логики предикатов, хотя здесь требуются и определенные дополнительные разъяснения. Прежде всего они связаны с отсутствием в формулах ЯЛП общих имен. Общие имена здесь используются только для характеристики задаваемой каждый раз при выражении некоторого высказывания области D значений предметных переменных. В составе самих формул общие имена – в предложениях обычного языка – заменяются предикаторами. Так, предложение «Все студенты пединститута готовятся стать преподавателями» может быть переведено на язык логики предикатов двояко в зависимости от выбора значений переменных. Мы можем взять в качестве таковой «множество студентов пединститута». Обозначив тогда через Р¹ свойство «готовятся стать преподавателями», получим  С учетом заданной области это должно быть прочитано как «всякий студент пединститута х готовится стать преподавателем». Для более полного выражения смысла высказывания можем взять в качестве области «студенты» вообще, а общее имя «студент пединститута» истолковать как предикатор, взяв для него, например, знак (предикатор) S¹ получим  Предложение звучит теперь так: «Для всякого студента х верно, что если он учится в пединституте, то он готовится стать преподавателем». Высказывание «Некоторые студенты пединститута готовятся стать преподавателями» при том же выборе области D и предикаторов запишется в виде  (В дальнейшем, как это обычно делается, будем опускать верхние индексы – указатели местности предикаторов, учитывая, что перечисление следующих за предикаторами аргументов указывает на эту местность предикатора, конечно, при правильно построении формул (что будет предполагаться).).

Обратите внимание, когда высказывание предваряет квантор общности (то есть исходное высказывание является общим), то далее используется логическая связка  в случае, когда таковым является квантор существования (высказывание является частным), то для его записи на ЯЛП употребляется связка &.

Для полной записи предложения «Во всяком государстве имеется город, который является его столицей» напрашивается необходимость ввести предикаторы: государство с аргументом – х (возьмем для обозначения из исходных символов предикатор Р¹), город с аргументом – у (обозначим его Q), принадлежит – город угосударству х (обозначим R²) и столица – город у государства х (обозначение S²). В таком случае возникает трудность с характеристикой области значений переменных х, у. Можно считать, что таковой является множество населенных людьми территорий. Взяв в качестве области D множество таких территорий и используя указанные предикаторы, получим запись нашего суждения в ЯЛП:  Буквальное произнесение его таково: «Для всякой населенной территории х верно, что если х есть государство, то существует населенная территория у, такая, что у – город и у принадлежит государству х, а у есть столица х.

Как мы видели, высказывания естественного языка, подлежащие переводу на ЯЛП, определенным образом стандартизируются, четко выделяются части высказывания: классы или отдельные предметы, о которых нечто утверждается (или отрицается). Если это классы, то выясняется, ко всем предметам класса или лишь к части их относится утверждение или отрицание (соответственно употребляются кванторы общности  или существования ). И наконец, определяется то, что именно в высказывании утверждается (или отрицается). Примеры таких стандартизации высказываний естественного языка, осуществленные еще до записи их на ЯЛП, читатель может найти в самом начале данного параграфа.

 

Упражнение

 

1. Выразите логические формы видов высказываний, приведенных на с. 133.

2. Укажите способ прочтения формул, полученных Вами в упр. 1, на языке логики предикатов.

 

ЛОГИКА ПРЕДИКАТОВ

Логика предикатов формируется аналогично тому, как это происходит относительно логики высказываний. При наличии определений логических констант – как логики высказываний, так и логики предикатов,– последняя определяется введением понятий логического следования для формул ЯЛП и закона логики предикатов.

ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ

Как и в логике высказываний, мы говорим, что для высказываний А₀ и В₀ (выраженных теперь в описанном языке логики предикатов), имеет место отношение логического следования А₀ ├ В_о, если и только если оно имеет место для формул А и В (А и В – метапеременные для формул ЯЛП.) представляющих собой логические формы указанных высказываний.

Последнее получается из А₀ и В₀ просто отвлечением от имеющихся значений их дескриптивных терминов. При этом возможно, что А₀ или В₀, а также и то и другое, содержат свободные переменные и трактуются при этом как высказывания с неопределенными истинностными значениями, в которых подразумевается, что каждая свободная переменная имеет какое-то определенное значение (во всех местах, где она встречается в том или ином выводе или доказательстве, или вообще в некотором рассуждении).

Очевидно, что в упомянутых высказываниях со свободными переменными эти переменные имеют условную интерпретацию, которой мы будем придерживаться и в дальнейшем, хотя не исключаем возможность употребления таких высказываний, например в выводах и доказательствах с интерпретацией всеобщности их свободных переменных. Строго говоря, именно условная интерпретация соответствует понятию логического следования. А в случае интерпретации всеобщности при построении выводов и доказательств, требуются особые ограничения.

Отношение следования между формулами A ╞ В имеет место е. т.е. при любой интерпретации дескриптивных терминов в А и В и при любых приписываниях значений свободным переменным при истинности первого истинно и второе, иначе говоря, ложно первое или истинно второе. Имеется в виду при этом, что, во-первых, если некоторый дескриптивный термин каким-то образом интерпретирован в А, то таким же образом он интерпретирован и в В (конечно, при наличии его в этой формуле), а, во-вторых, всем свободным вхождениям одной и той же переменной в А и В приписывайся одно и то же значение.

Из множества высказываний Г₀ следует высказывание В₀ если и только если это отношение имеет место соответственно между множеством формул Г и В, представляющих собой логические формы упомянутых высказываний. Последнее же отношение Г ╞ В имеет место, е. т. е. в составе Г имеется конечное подмножество формул А₁, ..., А_n (n ≥ 1) такое, что (A₁ & ... & А_n) ╞ В. Последнее соотношение, как и в логике высказываний, равносильно тому, что из множества высказываний А₁, А₂, ..., А_nследует В, что в свою очередь указывает на отмеченное ранее – в логике высказываний – свойство отношения следования, состоящее в том, что если некоторое высказывание следует из какого-то множества высказываний, то оно является следствием также любого расширения этого множества.

 

ЗАКОН ЛОГИКИ ПРЕДИКАТОВ

Формула А описанного языка логики предикатов является законом данной логической системы, то есть (╞ А) е. т.е. при любой ее интерпретации и при любых приписываниях значений ее свободным предметным переменным в заданной области D. Получаемое высказывание является истинным. Законы логики предикатов называются также универсально-общезначимыми формулами логики предикатов.

• Формула А называется общезначимой в некоторой области D е. т.е. она истинна при любых приписываниях значений ее дескриптивным терминам и свободным переменным в этой области D. Формула А называется выполнимой, если она истинна при какой-нибудь интерпретации и при каком-нибудь приписывании значений ее свободным предметным переменным. В противном случае она называется невыполнимой.

Поскольку в язык логики предикатов, как это иногда делается, мы не включаем пропозициональные переменные, никакая формула логики высказываний не является формулой логики предикатов. Однако из любого закона логики высказываний получается закон логики предикатов при подстановке вместо пропозициональных переменных любых формул логики предикатов (при замене каждого вхождения какой-нибудь пропозициональной переменной одной и той же формулой логики предикатов; хотя не исключается при этом замена разных пропозициональных переменных одной и той ясе формулой логики предикатов).

Так же, как и в логике высказываний, здесь введением указанных понятий – законов логики предикатов и логического следования – в сочетании с определениями логических констант задается бесконечное множество случаев отношения логического следования и бесконечное множество законов логики. Однако в отличие от логики высказываний мы не имеем теперь общих процедур для решения вопросов о том, имеет ли место отношение логического следования между множеством формул Г и формулой В (или между двумя формулами А и В) и является ли некоторая формула А законом логики. Эта специфика логики предикатов характеризуется как неразрешимость этой теории относительно универсальной общезначимости формул. Эта ограниченность наших возможностей здесь является платой за отказ от принимаемых в логике высказываний абстракций относительно структур некоторых высказываний.

Как и в логике высказываний, мы имеем здесь связь между отношением следования и законами логики. Она позволяет сводить вопрос о наличии или отсутствии отношения следования для конечных множеств формул к вопросу о том, является ли некоторая формула универсально общезначимой. Имеется в виду связь

 

 

В связи с отмеченной неразрешимостью логики предикатов особое значение приобретает здесь формализация понятий следования и закона логики посредством построения логических исчислений. Именно исчисление дает возможность во многих случаях синтаксическим образом решать вопрос, является ли некоторая формула законом, или соответственно есть ли некоторое отношение следования, когда мы не можем решить этот вопрос посредством семантического анализа. Для логики высказываний исчисление высказываний, вообще говоря, не является необходимым. Оно скорее нужно как часть логического исчисления для формул ЯЛП.

ИСЧИСЛЕНИЕ ПРЕДИКАТОВ

В основе исчисления предикатов лежит язык логики предикатов. В остальном оно является расширением исчисления высказываний.

Аксиоматическую систему исчисления предикатов мы получим, добавив к перечисленным выше схемам аксиоматического исчисления высказываний (имея в виду, конечно, переход к языку логики предикатов) следующие четыре схемы и одно правило:

 

 

НАТУРАЛЬНАЯ СИСТЕМА ИСЧИСЛЕНИЯ ПРЕДИКАТОВ

Постулатами системы (исходными правилами) являются все правила натуральной системы исчисления высказываний и правила для кванторов. Как и раньше, мы используем понятие зависимости формул в выводах от имеющихся в выводах допущений; точнее говоря, это понятие, определенное ранее для исчисления высказываний, расширяется в формулировках правил для кванторов.

Правила вывода для выражений с кванторами:

 

 

¹В других системах – без характеристик зависимости – это правило формулируется в виде явно непрямого: оно позволяет вместо вывода В из допущений  заключать о наличии нужной здесь выводимости на основании вспомогательного вывода, представляющего выводимость Г, А(х) ├ В, что значительно проще. Ситуация здесь аналогична той, что связана с правилом v_и.

 

Понятие вывода и доказательства остаются формально теми же, которые были сформулированы в исчислении высказываний, разница лишь в том, что при ссылке на правила вывода теперь имеются в виду и вновь введенные правила для выражений с кванторами. К числу указанных в предыдущем параграфе эвристических принципов введения допущений может быть добавлен еще один.

 

 

Сформулированное здесь исчисление, как и приведенная выше аксиоматическая система исчисления предикатов, представляет собой адекватную формализацию понятий логического следования и закона логики. Это значит, что для них справедливы теоремы:

 

Г ╞ В е. т. е. Г ├ В и ╞ А е. т. е. ├ А.

 

В заключение параграфа в дополнение к ранее сформулированным эквивалентностям языка логики высказываний приведем схемы наиболее важных законов логики, относящихся к языку логики предикатов, которые читатель может использовать также в качестве упражнений для выводов и доказательств:

 

 

 

Упражнение

 

Укажите эквивалентности, применяемые на каждом шаге преобразований в вышеприведенном примере.

Разработанный в современной символической логике метод построения логических исчислений является важнейшим ее результатом. Его теоретическая и практическая значимость состоит в том, что благодаря ему возникает возможность доказательства любой формулы, представляющей закон логики, из бесконечного множества таких формул, а также осуществлять соответствующий вывод для любого случая – опять-таки из бесконечного множества случаев – отношения логического следования. В основе логических исчислений, как мы видели, лежат специальные логические языки. Наряду с рассмотренными выше возможностями использования этих языков для решения многих логических вопросов, и в первую очередь для точного определения основных понятий логики (логическое следование и закон логики), следует заметить, что в этих языках имеются, по существу, точные понятия логической формы и логического содержания мыслей, которые мы используем в дальнейшем.

 

Упражнения

 

Постройте доказательства следующих формул:

 

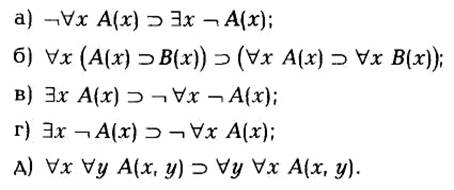
ТИПЫ ОБЪЕКТОВ ПОЗНАНИЯ И ИХ ВОЗМОЖНЫЕ ХАРАКТЕРИСТИКИ

§ 12. Возможные объекты познания (предметы мысли)

Мы уже отмечали, что в каком-то смысле многообразие предметов познания шире, чем многообразие предметов действительности. Неумение правильно оперировать с предметами мысли и неумение различать предметы разных типов может приводить к нелепым рассуждениям типа: «Человек произошел от обезьяны. Н.– человек, следовательно, Н. произошел от обезьяны», или «Иванов – токарь, токарь – не слесарь, значит, Иванов – не токарь».

Относительно объектов познания читателю следует вспомнить то, что было сказано о предметных значениях знаков, в особенности, о предметных значениях единичных и общих имен (5 и 6 гл. II). Напомним, что предметами познания могут быть не только вещи, явления, процессы реального мира, но и их свойства, отношения, а также воображаемые объекты, продукты мыслительной деятельности и т.д., и т.п. Предметом в широком смысле слова, как мы помним, является все, что обозначено именем. Давая чему-либо имя, мы превращаем его в предмет мысли. Именем же можно обозначить все, что обладает некоторой качественной определенностью, то есть имеет какие-то характеристики или их совокупности, отличающие это нечто от всякого другого и позволяющие мысленно или, по крайней мере, чувственным образом выделить его и рассуждать о нем. Разнообразие объектов, как возможных предметов мысли, можно, по-видимому, свести к следующим основным видам:

Во-первых, мы делим их на эмпирические и теоретические в зависимости от того, каким образом, за счет какого источника познания (орган чувств или мысленно-интеллектуальная деятельность) они вводятся в состав нашего знания.

Эмпирические объекты познания – это реальные, чувственно-воспринимаемые, наблюдаемые предметы действительности.

Как объекты теории – это результаты наблюдения и вообще чувственной деятельности, хотя, как мы уже говорили, при характеристике эмпирического уровня познания они могут быть уже в той или иной степени «обработаны» нашим мышлением. Сюда относятся:

1. ВЕЩИ – индивиды (люди, реки, минералы), системы объектов (созвездия, планетные системы), более или менее цельные ситуации (противостояние планет, те или иные взаиморасположения планет, сезонные состояния природы и т.п.).

2. СОБЫТИЯ (явления) – гром, молния, солнечное затмение и т.п.

3. ПРОЦЕССЫ – испарение, похолодание, рассвет, перемещение материков и т.д.

Это различение, конечно, является примерным.

Эмпирические объекты познания иногда характеризуют как наблюдаемые объекты, а обозначающие их термины – как термины наблюдения.

Источником появления теоретических объектов познания является наша мыслительная деятельность.

К теоретическим объектам познания относятся:

1. Реальные – по крайней мере по предположению при их введении – объекты, то есть объекты, которые вводятся мышлением при построении объяснительных теорий. Объясняя, например, тепловые явления, химические превращения, излучение или поглощение света, процессы и явления, связанные с изменением агрегатных состоянии тел, и другие явления в области физики макротел, вводятся такие объекты, как молекулы, а затем и атомы (особенно при объяснении химических взаимодействий), далее – электроны и атомные ядра, нейтроны, протоны и т.д. Эти объекты, по крайней мере до некоторых пор в развитии теории, имеют гипотетический характер. Иногда оказывается, что какие-то из них не существуют в действительности и исключаются из сферы теории (флогистон, теплород, жизненная сила и т.п.). 2. Абстрактные объекты – два основных вида:

а) объекты, возникающие в познании при интенсиональном употреблении имен (см. § 8);

б) объекты, представляющие собой некоторые свойства или отношения (характеристики вообще) предметов действительности, превращенные в самостоятельные предметы мысли,– результаты изолирующего абстрагирования (упругость, электропроводность, теплопроводность и теплопроводность меди, вращение и вращение Земли, любовь, дружба, красота, числа, геометрические фигуры и т.д.).

ЗАМЕЧАНИЕ. Обратим внимание на одно широко распространенное в философии недоразумение. Утверждают часто, что объектами научного познания никогда не являются реальные приметы действительности. Даже в тех случаях, когда, по-видимому, мы изучаем реальные предметы действительности (животные, растения, металлы), мы фактически имеем дело в теории уже с результатами определенной логической обработки этих предметов. И утверждения науки относятся к этим так называемым абстрактным объектам. В этом случае не различают: 1) КАК мы можем оперировать объектами в процессе познания и то, 2) ЧТО является объектами нашего изучения.

Пользуясь языком как средством познания, обозначая предметы и их свойства и отношения посредством знаков языка, мы определенным образом огрубляем их, поднимаем их, как выразился А.И. Герцен, из сферы частностей в сферу всеобщностей. Обобщая предметы в понятиях уже даже на эмпирическом уровне познания, мы представляем их (опять-таки в языке) в той или иной мере абстрактно, обобщаем их лишь по тем или иным общим для предметов некоторого класса признакам, отвлекаясь от имеющихся в этом классе различий (см § 15). В этом смысле мы всегда, конечно, имеем дело не с конкретными предметами (во всей совокупности их признаков). Но данные представления предметов в языке являются лишь необходимым средством представления конкретных, реальных предметов действительности. И конечно, когда мы говорим, например, что все люди нуждаются в пище, пользуясь общим понятием человека, в котором все люди определенным образом отождествляются,– мы говорим не об этих абстрактных людях, а о реальных – существующих в пространстве и времени: в пище нуждаются не абстрактные, а конкретные, живые люди!

Итак, в этом разделе мы говорим об объектах познания и лишь некоторые из них действительно являются абстрактными.

3. Идеализированные объекты познания – результаты определенного типа мысленной «обработки» предметов реальной действительности – идеализации (абсолютно черное тело, идеальный газ, абсолютно упругое тело и т.п.). Мысленная «обработка» состоит здесь в том, что мы наделяем реально существующие предметы некоторыми свойствами, которых они в действительности не имеют (тело, поглощающее все падающие на него лучи – абсолютно черное тело), или лишаем их некоторых свойств, которыми они обладают в действительности (тело, абсолютно не проводящее электрический ток). Впрочем, «лишение» и «наделение» – обычно операции относительные: лишение предмета одного свойства означает наделение его другим и наоборот (абсолютно гладкая плоскость – то же, что плоскость не вызывающая трения; тело, поглощающее все лучи – тело, не отражающее никаких лучей, и т.д.).

Существуют объекты, которые одновременно являются и абстрактными и в то же время идеализированными объектами познания – таковы, например, геометрические фигуры, как они мыслятся в геометрии. Чтобы представить себе, насколько широк круг идеализированных объектов в познании и даже в повседневной практике вспомните о том, как мы идеализируем наших друзей и любимых, об идеализации событий и фактов истории и т.д.

Особый вид идеализированных объектов составляют классы, множества как предметы мысли. В реальной действительности класс тех или иных предметов, например, металлов, растений, животных – это совокупности в каком-то отношении качественно-однородных предметов, существующих в разных местах, в разное время, обычно с постоянно изменяющимся составом. Превращая их в предметы мысли, мы мысленно «собираем» их в нечто единое, в единую совокупность как бы одновременно и в одном месте существующих предметов. Но существующих отдельно и независимо Друг от друга. Когда же предполагается какая-то связь между предметами множества, таких, например, как семья, футбольная команда, производственный коллектив,– тогда такое множество называется агрегатом.

4. Идеальные объекты познания – результаты творческой деятельности мышления, не имеющие прообразов в действительности.

Выделяются два вида идеальных объектов:

А. Мысли, знания, информация. Они имеют, безусловно, некоторые прообразы в действительности по содержанию, поскольку в них воспроизводятся какие-то аспекты действительности, но не имеют прообразов как особого рода объекты познания.

Идеальными считают иногда также и формы, приемы познания. Точнее, их скорее надо относить к числу абстрактных объектов, хотя бы потому, что они не являются, как правило, продуктами нашего мышления.

Абстрактные и идеальные, идеальные и идеализированные объекты обычно вообще не различают, называя все их идеальными. Нужно признать, что различие этих видов, как впрочем и разграничение видов предметов в реальной действительности – отнюдь не всегда теоретически простая задача. Часто существенно лишь само знание о существовании объектов качественно различных типов.

Б. Объекты играющие чисто инструментальную роль в познании – системы координат, тензоры, векторы, параллели, меридианы и т.п.

В данном случае мы говорим здесь о них как об объектах познания в том смысле, что имеем дело с ними в процессе познания (хотя они могут быть и в ряде случаев являются также объектами изучения).

ТЕОРЕТИЧЕСКИЕ ОБЪЕКТЫ ПОЗНАНИЯ И ВОПРОС О НЕПУСТОТЕ ТЕРМИНОВ

Проблема, которая здесь имеется в виду, относится к абстрактным, идеализированным и особенно к идеальным объектам. Она заключается в вопросе о том, имеют ли обозначающие их термины предметные значения, то есть являются ли они пустыми или не являются таковыми? Вопрос возникает в силу именно того, что идеальные объекты не имеют даже прообразов в действительности, абстрактные не существуют как самостоятельные, идеализированные не существуют как таковые. Мы обращаемся здесь к этому вопросу потому, что нередко можно встретить мнение о том, что именно в этих случаях мы имеем дело с пустыми терминами. Однако мы уже раньше говорили о том, что пустые термины характеризуются тем, что высказывания, содержащие их, по крайней мере, в качестве логических подлежащих, лишены реального содержания: они не истинны и не ложны и, значит, не являются осмысленными (Исключения составляют так называемые экзистенциальные высказывания, в которых утверждается существование или несуществование, возможность или невозможность тех или иных объектов (см. § 29). Указанное мнение о неосмысленности высказываний с пустыми терминами в качестве логических подлежащих, разделяют не все логики. Существуют даже логически-дедуктивные теории, так называемые свободные логики (логики, свободные от экзистенциальных допущений), в которых допускаются высказывания (и выводы из них) именно с пустыми терминами и относящиеся к пустым областям предметов.

Поскольку возможны вообще рассуждения, оторванные от реальной деятельности, постольку имеет некоторое теоретическое значение и описание их. Но по существу – это рассуждения, которые рождают лишь одни словосочетания из других. Они бесполезны как практически, так и теоретически.

Иного рода системы представляют, например, так называемые силлогистические теории, в которых суждения с пустыми терминалами допускаются наряду с обычными. При этом, стремясь придать таким суждениями некоторую осмысленность, сами авторы систем вводят конвенциальным образом те или иные критерии их истинности (см. § 36).). Однако, вводя в свои теории объекты указанных типов, ученые в каждом случае определяют критерии истинности или ложности содержащих их высказываний. Установление таких критериев для абстрактных объектов не представляет обычно особых сложностей. Для идеализированных тем более, поскольку суждения, относящиеся к идеализированным объектам,– это случаи более или менее точного, приблизительного знания о реальных предметах действительности. Что касается идеальных, то активность нашего познания и специфика отражения мира в мышлении в связи с этими объектами доходят до того, что они часто включаются даже в число реальных предметов действительности. Примерами этого могут служить суждения «Полярная звезда находится в одной из точек пересечения небесной оси с небесной сферой», «Москва находится между 54 и 55 параллелями северной широты» и т.п. Таким образом, рассматриваемые термины отнюдь не являются, конечно, пустыми. И очевидно, что истинность таких утверждений нетрудно установить, зная, например, где «проходят» на Земном шаре соответствующие параллели.

Но истинность таких высказываний в проективной геометрии, что две параллельные прямые пересекаются в бесконечно удаленной точке и что через две бесконечно удаленные точки можно провести единственную прямую, а именно бесконечно удаленную,– это уже конвенциальные истины (то есть истины, принимаемые по соглашению). Однако конвенция в составе системы утверждений и в соответствии с этой системой – это не просто произвол. А инструментальная роль таких идеальных объектов как бесконечно удаленные точки и бесконечно удаленная прямая состоит в проективной геометрии лишь в том, чтобы придать общность основным утверждениям этой геометрии.

Это нужно для того, в частности, чтобы избегать таких, например, оговорок для обычной эвклидовой геометрии, что общую точку имеют любые две прямые на плоскости кроме параллельных. Аналогична инструментальная роль таких идеальных объектов теории чисел и алгебры как мнимое число и комплексное число.

Понятие признака. Виды признаков

Наряду с множеством возможных предметов мысли существует также множество способов их мысленного выделения, обусловленное многообразием их возможных характеристик. Речь идет прежде всего о некотором многообразии типов возможных характеристик предметов или, как их принято называть в логике, типов признаков предметов. Знание этих типов позволяет, во-первых, уяснить многообразие мысленных способов выделения предметов (результатами такого выделения являются понятия), а, во-вторых, оно весьма существенно для понимания смыслов высказываний (суждений) о предметах.

Признаками в логике называют любые возможные характеристики предметов, все, что можно высказать о предмете. В объектной действительности это все то, в чем одни предметы сходны между собой, другие – различны. Сходство и различие предметов в самой действительности служат объектным основанием для отождествления и различения их по соответствующим признакам в процессе познания. Признаком может быть наличие или отсутствие у предмета того или иного качества, свойства, состояния и т.п. или отношения предмета к другим предметам. Так, признаками металлов являются их кристалличность (качество), хорошая электропроводность (свойство), а также то, что они не являются сложными веществами (отсутствие качества); признаком Парижа является наличие у него такого отношения (к Франции как государству) как «быть столицей», а одним из признаков Лиона – отсутствие такого отношения.

Качественная определенность вещей позволяет характеризовать их как некоторые системы признаков и мысленно выделять их таким образом, отличая от всего остального. Каждый читатель без труда может, очевидно, указать множество характеристик своих друзей и известных ему предметов, и при этом он заметит, что иногда характеристики сводятся к наличию каких-то черт, а иногда – к их отсутствию. В качестве упражнения предлагается здесь осуществить подобную процедуру хотя бы по отношению к самому себе, как наиболее знакомому для читателя предмету.

В истории философии и логики постоянно предпринимались попытки выделения основных типов возможных характеристик объектов. Аристотель, например, усматривал 10 типов таких характеристик, которые называл категориями, а также предикабилиями: сущность или субстанция (человек, лошадь); количество (в два локтя); качество (белое); отношение (двойное, большее); место (на площади, в Ликее); время (вчера); положение (лежит, сидит); состояние (обут); действие (разрезает); страдание (разрезается). Однако столь детальная дифференциация признаков едва ли необходима. Перечень их у Аристотеля является к тому же неполным.

В современной логике все указанные характеристики, как и все другие характеристики отдельного предмета, обобщенно называют свойствами. Свойства, в данном широком смысле, то же самое, что признак, когда речь идет о характеристиках именно отдельных предметов. Оно отличается от отношения, представляющего собой характеристику (признак) не отдельного предмета, а характеристику некоторых систем – пар, троек, четверок, вообще, n-ок предметов. Таковы отношения «брат», «отец», «сын», «находится между», «параллельный» и т. п. Конечно, у читателя должен возникнуть вопрос, как же определить, что такое свойство и что такое отношение? Ответ на этот вопрос можно дать, указав специфику представляющих их знаковых форм. Знаками свойств – в Указанном широком смысле – являются одноместные предикаты. В формализованном языке – это высказывательные формы с одной свободной переменной (Следует различать предикаты и предикаторы. Последние являются составными частями предикатов (см. § 1, гл. III). Ранее, в § 6 гл. II, мы характеризовали сами предикаторы как знаки характеристик (свойств и отношений) предметов, а также знаки предметных функторов (характеристик предметно-функционального типа). Там имелись в виду характеристики общего плана – без соотнесения их к определенным предметам. Здесь же рассматриваются типы характеристик именно определенных, отдельных, данных предметов, и таким образом,– конкретные формы таких применений. Все эти формы, как видно из рассматриваемой классификации, представляют собой одноместные предикаты.), то есть выражение типа: «город (х)», «твердый (х)», «электропроводник (х)»,  (свойство быть отцом кого-то). В естественном языке формы такого рода специально не выделяются, что затрудняет его применение для логического анализа. Однако при желании их можно выделить, употребляя общие имена вместо специальных символов для переменных, при этом иногда с числовыми индексами для экземплификации предметов: «населенный пункт есть город», «человек₁ (мужчина), отец какого-то человека₂) и т.п. Знаками отношений являются многоместные (двух-, трех- и т.д.– местные) предикаты, то есть высказывательные формы более чем с одной свободной переменной. Например, «столица (х, у)», «мать (х, у)», «отец (х, у)», «находится между (х, у, z)» («х находится между у и z»).

В пределах введенного обобщенного понятия свойства полезно теперь выделить некоторые виды характеристик отдельных предметов (признаков данных предметов или, что то же, свойств предметов в широком смысле этого слова). Мы разделим при этом признаки отдельных предметов на простые и сложные, а простые в свою очередь на положительные и отрицательные, атрибутивные и реляционные, пропозициональные и предметно-функциональные. Среди последних – выделим также характеристики качественного и количественного типа.

Простые и сложные признаки различаются по форме представляющих их предикатов. Простыми назовем такие признаки, знаки которых (предикаты) не содержат логических констант: 

В противном случае, признак называется сложным, например: «студент (х) & живет (х, Москва)» – человек является студентом и живет в Москве; «делится (х, 2)  четно (х)» – число делится на 2 или не является четным. Ясно, что составляющие приведенных выражений являются простыми признаками (свойствами).

Дальнейшее деление признаков отдельных предметов осуществляется лишь для простых признаков.

Также по форме предикатов, представляющих простые признаки, делим их на положительные и отрицательные. Признак называется положительным, если представляющий его предикат не содержит знаков отрицания (или содержит четное число таковых (По закону логики – согласно которому  эквивалентно А – при наличии четного числа отрицаний в предикате все они могут быть исключены. А при наличии нечетного числа отрицаний можно исключить все, кроме одного.)). В противном случае – при наличии нечетного числа отрицаний – признак называется отрицательным. Например, «  у столица (х, у)», (где область значений х – города, а у – государства) – положительный признак; в естественном языке – «город является столицей некоторого государства». «  у столица (х, у)» («город не является столицей какого-либо государства») – отрицательный признак.

Важное значение в процессе познания имеет различение атрибутивных и реляционных свойств (признаков). Первые представляют собой характеристики предметов самих по себе, например, «является человеком», «жидкий», «способный», «неспособный» и т.п. Реляционные свойства указывают на наличие или отсутствие отношения данного предмета к каким-то другим предметам: «столица (х, Кубы)», «  столица (х, у)» («город является столицей Кубы», «город является столицей какого-нибудь государства»). Нетрудно заметить, что одноместный предикат, который представляет реляционное свойство, образуется из многоместного – в последних двух случаях из предиката «столица (х, у) (Из предиката с некоторым числом мест более одного образуется предикат с меньшим числом мест посредством устранения каких-то его свободных переменных. Устранить некоторую свободную переменную можно, либо связывая ее каким-то из кванторов, либо подставляя на места всех ее свободных вхождений в формулу имя какого-то предмета из области значений этой переменной (постоянного терма – терма, не содержащего переменных). Из одноместного предиката таким образом получается высказывание (высказывание характеризуется иногда как ноль-местные предикаты).)».

Таким образом, реляционное свойство образуется всегда из некоторого отношения.

В другом плане, в зависимости от того, использованы ли для образования свойств пропозициональные или предметно-функциональные характеристики (6, гл. II), мы получаем соответствующие им характеристики отдельных предметов и формы предикатов. Употребляя, например, предикаторы «логичный», «научный» (то есть характеристики пропозиционального типа) можем образовать предикаты (признаки, свойства): «логично (х)» (где область значений х – рассуждения; в естественном языке – «рассуждение логично»); «научно (х)» (возможные значения х – утверждения; в естественном языке – «утверждение научно»). Читателю рекомендуется просмотреть примеры всех предшествующих делений понятия признака для того, чтобы убедиться, что все они относятся к числу характеристик пропозиционального вида, то есть все они образованы из предикаторов – знаков свойств и отношений.

Используя теперь предметно-функциональные характеристики (знаки, представляющие собой предметные функторы), например, «возраст» и «темперамент», получаем предикаты: «= (возраст (х), 17 лет)»; « = (темперамент (х), флегматик»). Область х во всех случаях – люди. В естественном языке соответственно: «Возраст человека равен 17 годам», «по темпераменту человек относится к флегматикам». Обратите внимание, что предикаты, образованные из предметно-функциональных характеристик, представляют реляционные свойства. Все они образованы в конечном счете из двухместных предикаторов «больше», «меньше», «равно».

 

Упражнение

 

Образуйте простые одноместные предикаты, положительные и отрицательные, используя предметные функторы: пол, профессия, образование, местожительство, память (у человека), внимание, национальность, способность, рост, талант, партийность.

Здесь мы подошли к важному различению признаков: а именно к разделению признаков на такие, которые представляют собой качественные характеристики предметов и те, что являются количественными характеристиками предметов. Эти различения имеют существенное значение в философии. В учении о диалектике развития есть даже специальный закон «перехода количественных изменений в качественные», согласно которому всякое качественное изменение является результатом некоторого количественного изменения.

Количественные характеристики представляют предикаты, образованные из предметных функторов, значения которых допускают сравнения типа: «больше», «меньше», «равно». Это значит, соответствующие этим характеристикам предикаты образованы посредством любого из этих отношений. При этом значения количественных предметных функторов могут быть, и обычно являются, числа с некоторой размерностью или некоторые градации (степени) типа: средний, высокий, низкий – для характеристик роста, температуры; высокая, низкая – для скоростей и т.п. Характеристики такого типа употребляются, в частности, в тех случаях, когда для значений соответствующих функторов не разработана (или не применима по тем или иным причинам) процедура измерения. Когда процедура разработана, функтор становится числовым. Функторы, представляющие количественные характеристики предметов, называются величинами.

Таким образом, признаки, представляющие собой количественные характеристики предметов, образуются с использованием предметных функторов – величин (наряду с предикаторами «больше», «меньше», «равно»). Все другие, то есть не количественные характеристики, в том числе и пропозициональные, называются качественными. Термины, представляющие собой величины, фиксируют и обобщенно представляют такие именно стороны предметов, относительно которых возможны указанные выше сравнения «больше», «меньше», «равно». Тогда как значения предметно-функциональных терминов другого типа (национальность, образование, пол, агрегатное состояние и т.п.) таковы, что о них можно говорить только, что какой-то предмет обладает или не обладает этим свойством: человек – москвич или не москвич; мужчина или не мужчина; образование у него высшее или не высшее. Аналогичным образом обстоит дело относительно тех характеристик предметов, которые обозначают предикаторы: любая плоская, замкнутая фигура является квадратом или не является им; дерево является хвойным или не является хвойным.

В философии среди качественных характеристик, которые представляют предикаторы, выделяют качества, свойства (в узком смысле этого слова) и отношения. В последнем случае имеется в виду отношение как реляционное свойство, то есть отношение не между какими-то предметами, а отношение данного предмета к каким-то предметам.

Качеством называют нечто, присущее предмету самому по себе (хотя оно возникло, возможно, в связи с другими предметами). Качеством некоторого предмета является то, что он представляет собой металл, дерево, жидкость и т.п., а также то, что он имеет кристаллическое строение, что в его составе имеются свободные электроны (как у металлов). Свойство есть проявление некоторого качества во взаимодействии предмета с какими-либо другими предметами. Так, наличие кристаллического строения у какого-либо вещества, то есть качества, проявляется при нагревании в том, что это вещество имеет определенную температуру плавления. Наличие свободных электронов при наличии электрического поля проявляется в том, что в веществе появляется электрический ток (поток электронов). Таким образом, наличие у вещества определенной температуры плавления, хорошая его электропроводность – это свойства. Точно так же цвет предмета есть его свойство, представляющее собой проявление некоторого качества отражающей способности поверхности предмета, то есть проявляющееся во взаимодействии со световыми лучами. Качество иногда характеризуют как структурное свойство предметов, однако это не всегда характеристика структурного характера. К качественным характеристикам человека относятся его характер, культурный и интеллектуальный уровень, наличие определенных принципов и т.д., а свойствами, представляющими собой проявление указанных и иных качеств, являются, например, вежливость, честность, аккуратность и т.д.

Наконец, среди свойств – в указанном узком смысле этого слова – полезно выделить так называемые диспозиционные предикаты. Это – способности предметов вести себя определенным образом в определенных ситуациях в силу некоторых имеющихся у них качеств. С понятием диспозиционного предиката связывают обычно представление о необходимости определенного поведения предмета при определенных условиях (растворимое вещество необходимо растворяется при погружении в воду, упругое тело необходимо восстанавливает форму и размеры при устранении деформирующих его сил). «Способность» же предмета вести себя некоторым образом в определенных ситуациях может не исключать лишь возможность предмета вести себя определенным образом, но не необходимо ведет себя так. Трусливый человек, например, может при наличии опасности проявить малодушие, отступить перед нею, но не обязательно поведет себя таким образом. В понятии свойства предмета подразумевается как необходимость, так и возможность для этого предмета вести себя при определенных условиях определенным образом.

 

Упражнение

 

Определите, какие из характеристик предшествующего упражнения являются качественными, а какие – количественными. Обоснуйте свой ответ.

 

Деление признаков по месту и роли в системе признаков. Сущность предметов

До сих пор мы рассматривали виды признаков, имея в виду множество возможных признаков вообще. Однако можно говорить о множестве признаков того или иного конкретного предмета или вида некоторых предметов (металлов, жидкостей, млекопитающих). Каждый предмет мыслится, вообще говоря, как некоторая субстанция. Однако его можно для некоторых научных целей рассматривать и как систему признаков (качеств, свойств, отношений, количественных характеристик). Более строго говоря, мы всегда имеем возможность рассматривать предмет как систему (множество) известных – на данной ступени познания – признаков. Среди таких признаков предмета прежде всего различаются случайные для него и неслучайные. Случайные обусловлены некоторыми внешними обстоятельствами и ни в какой мере не определяют качественную специфику предмета. Случайными признаками металлов, например, являются наличие тех или иных примесей, та или иная их температура в определенных ситуациях. То же можно сказать о воде. Для человека случайными могут быть – особенно при командно-бюрократической организации общества – то или иное его служебное положение, окружение и т.п.

Между неслучайными признаками существуют внутренние для данных предметов связи: одни из них обусловливают другие. Их множество представляет собой таким образом некоторую систему. Для предметов некоторого вида, и тем более для отдельных конкретных предметов, это множество бесконечно. Иное дело множество признаков этого рода, познанных на том или ином этапе развития знания. Оно всегда конечно, причем в определенных случаях – при относительно завершенности процесса познания предметов на некотором этапе – это множество также представляет собой определенную систему, по крайней мере когда речь идет о признаках некоторого вида предметов (вопрос о том, в какой мере это относится к признакам отдельных предметов, является для науки пока открытым). Одни признаки здесь обусловливают другие, эти последние – третьи и т.д. В силу этих отношений субординации одни признаки системы можно охарактеризовать как более существенные, другие – как менее существенные.

Системами указанного типа являются, например, множества известных признаков металлов, жидкостей, признаков, характеризующих общественное устройство. Наличие ионной кристаллической решетки у металлов обусловливает их ковкость, пластичность; в силу наличия свободных электронов в массе металла они являются хорошими проводниками электрического тока; благодаря наличию кристаллического строения металлы, как и другие кристаллические вещества, имеют определенную температуру плавления.

Среди неслучайных признаков предметов можно выделить совокупность некоторых наиболее существенных – основных признаков, обусловливающих все остальные, общие для данных предметов. Из этой совокупности, в сочетании с известными законами соответствующей области действительности, могут быть логически выведены все известные общие для данных предметов и неслучайные для них признаки, а для абстрактных объектов – в так называемых полных теориях – вообще все признаки, общие для предметов вида.

• Совокупность основных существенных признаков того или иного вида конкретных предметов действительности называется их СУЩНОСТЬЮ.

Так, сущностью металлов, как химически простых веществ, является то, что они состоят из однородных атомов, а именно атомов с одним и тем же зарядом ядра, и атомы их обладают низким потенциалом ионизации, в силу чего легко теряют свои внешние электроны. Этим обусловлены общие для металлов химические свойства, особое строение их кристаллической решетки, хорошая электропроводность, пластичность и т.д.

Основным признаком общества (его сущностью) является господствующий в нем способ производства, характеризующийся определенным уровнем развития производительных сил и типом производственных отношений, то есть тем, что называется экономическим базисом общества. Экономический базис общества определяет характер господствующих в обществе политических взглядов, правовых отношений, идеологии, морали.

Сущность предметов некоторого качества (предметов некоторого класса), выявленная на некотором уровне познания, является основой качественной специфики этих предметов, но лишь в той мере, в какой эта специфика нам известна на данном этапе познания. Исходя из этой сущности мы можем объяснить известные общие, специфические для данных предметов (неслучайные) их признаки. В процессе дальнейшего развития знания о соответствующих предметах открываются новые качества, свойства предметов, отношения их к другим предметам, которые нельзя объяснить исходя из познанной сущности. В таком случае происходит – в результате поиска нужных объяснений – проникновение в «более глубокую» сущность предметов, открытие таких же признаков, исходя из которых могут быть объяснены все известные ранее и вновь открытые их особенности. Таким образом, существуют сущности разных уровней или порядков.

В истории философии имело широкое распространение представление о том, что у предметов того или иного вида или даже отдельных предметов имеется некоторая абсолютная сущность, основа всех его признаков. Эта «последняя сущность» должна быть, согласно этим представлениям, пределом познания соответствующих явлений. На такое понимание наводит нередко встречающееся в философской литературе определение сущности как некоторого внутреннего содержания вещи, определяющего специфику ее многообразных проявлений.

Однако исторический опыт развития знания указывает на другое, а именно на то, что сущность предмета в диалектическом ее понимании – это есть лишь тот предел, до которого дошло познание предмета на данной ступени развития знания. Познание мира, как и отдельных его областей и явлений, есть бесконечный процесс углубления знания. А это означает, что сущность может быть менее и более глубокой, и этим, в частности, объясняется смена одних теорий другими,– более высокого порядка.

Так, еще в недалеком прошлом свет в физике понимали как поток волн электромагнитного излучения определенного диапазона частоты. Но при этом не объяснялись некоторые открытые позже явления, например, явление фотоэффекта. В настоящее время господствует уже корпускулярно-волновая теория света, согласно которой свет представляет собой поток фотонов, обладающий как волновыми, так и корпускулярными свойствами.

Окисление какого-либо вещества понималось до некоторых пор как присоединение к атомам данного вещества атомов кислорода. В настоящее время этот механизм соединения атомов объясняется как результат взаимодействия внешних электронов атомов. Вообще на некотором этапе от понимания химических реакций как взаимодействий между атомами веществ произошел переход к пониманию их как взаимодействия внешних электронов и образующихся при этом ионов веществ.

Совокупность основных, существенных признаков может быть выделена также, по-видимому, в любом случае, в множестве признаков, общих для абстрактных предметов того или иного вида,– геометрических фигур, чисел, алгебраических систем и т.п. Для ромбов, например, это то, что указывается в определении фигур этого вида (и соответственно в содержании понятия ромба): плоская геометрическая фигура, замкнутая, ограниченная четырьмя сторонами, все стороны которой равны. В аксиоматической теории алгебраических систем того или иного вида (теории групп, булевой алгебры и т.д. и вообще в теории некоторой структуры, например, в геометрии, как математической, формальной теории) эту совокупность признаков (и соответственно содержание понятия рассматриваемой структуры) представляет множество аксиом. Однако эту совокупность признаков неправомерно, видимо, рассматривать как сущность структуры соответствующего вида, поскольку для одного и того же множества признаков, общих для структур некоторого вида, существует, вообще говоря, не одна такая совокупность. Так вместо указанной совокупности, основных существенных признаков ромба может быть другая, получающаяся из нее заменой признака «равносторонняя фигура» на «фигура, диагонали которой взаимно перпендикулярны и в точке пересечения делятся пополам». Известно также, что существуют эквивалентные теории с различными составами аксиом. Неестественно, конечно, было бы считать, что объекты одного и того же типа имеют на одном и том же уровне познания различные сущности.

Специфическими являются случаи, когда дело касается предметов, созданных людьми для тех или иных определенных целей. Обычно сущность такого рода предметов усматривают именно в их назначении, что отражается в определениях. Часы – это прибор, с помощью которого можно отсчитывать время; термометр – прибор, служащий для измерения температуры, и т.д. Назначением предмета определяются и все его другие качества. Это и служит причиной того, что оно принимается за сущность. Хотя верно и другое: благодаря наличию определенных качеств (особому устройству) та или иная вещь выполняет определенные функции. Качества вещи, предназначенной для определенной цели, вытекают из ее назначения логически. Способность же вещи служить определенной цели обусловлена ее качеством фактически, как действие – причиной. Но поскольку человек мысленно конструирует вещь прежде, чем создает ее, и при этом выводит все ее качества именно из предназначения вещи, то это последнее оказывается решающим. Здесь, как видим, сущность вещей определяется практическими потребностями людей. Но это не указывает на субъективный характер данного понятия, поскольку сами вещи, которые здесь имеются в виду, создаются людьми именно для удовлетворения своих потребностей.

В любом случае основные существенные признаки предметов некоторого вида составляют основу их качественной специфики, поскольку они обусловливают все другие общие и, в совокупности, специфические для данных предметов признаки. В случае конкретных предметов действительности обусловленность имеет причинный или целевой характер, в случае абстрактных объектов – структурный или функциональный характер. Но в том и другом случае из совокупности указанных основных признаков в сочетании с законами данной области действительности все другие неслучайные признаки предметов выводимы логически.

Сущность предметов того или иного вида составляют обычно признаки, недоступные наблюдению. Они выявляются теоретическим способом именно в результате построения и обоснования теории, объясняющей известные признаки изучаемых предметов. Кстати, именно в процессе построения такой теории прежде всего происходит отделение неслучайных признаков от случайных. Случайные выделяются тем, что не поддаются объяснению и не вписываются в возникающую при построении теории систему.

Еще в XVIII веке возник, например, вопрос о сущности воды. Речь шла именно о том, как объяснить известные в то время общие для всех случаев существования воды ее свойства. Основой обобщения всех этих случаев под общим названием – именем «вода» – являлось первоначально практическое использование воды и связанная с этим обобщением интуиция. Как обычно при построении теории возникло несколько гипотез. Одна из них, которая затем получила теоретическое и экспериментальное подтверждение и стала общепризнанной,– гипотеза Лавуазье о том, что вода есть химическое соединение кислорода и водорода. Экспериментальным подтверждением оказалось получение воды из «гремучего газа». При этом как раз выяснилось, что наблюдаемые в различных случаях примеси воды не связаны с ее сущностью, то есть представляют собой случайные признаки. Углублением знания сущности воды, указанной Лавуазье, стало в дальнейшем понимание того, что вода есть химически сложное вещество, молекулы которого состоят из двух атомов водорода и одного атома кислорода. При этом удалось объяснить и такое примечательное свойство воды, как сжатие ее при нагревании от 0°С до 4°С, обусловленное перестройкой молекулярной структуры воды в этом температурном промежутке.

Итак, в системе познанных признаков некоторого вида выделяются: 1) основные, существенные признаки для конкретных предметов действительности, составляющие их сущность; 2) производные – обусловленные основными, а также 3) случайные признаки. Явно несостоятельным является также определение в философской и логической литературе сущности предмета как того, что необходимо принадлежит предмету, без чего он не может существовать, не может быть тем, что он есть. Попытка применить его практически обнаруживает даже, что оно содержит скрытый круг. Попробуем, например, руководствуясь им, выделить существенные признаки квадрата. Для этого нужно установить, без каких признаков ту или иную фигуру нельзя отнести к квадратам. Но это уже требует знания существенных признаков квадрата. Мы не назвали бы квадратом, например, четырехугольник, углы которого не являются прямыми, а стороны равными, но именно потому, что знаем, что эти признаки являются существенными для квадрата.

Вообще, для решения вопроса о том, без каких признаков предмет не был бы тем, что он есть, надо знать, чем именно этот предмет является, какими существенными признаками выделяется из числа других предметов.

Если сущность предмета выявлена, то оказывается, что одни признаки необходимо принадлежат ему, потому что вытекают из сущности, другие являются случайными, потому что не связаны с нею. Из определения квадрата как прямоугольного и равностороннего четырехугольника с необходимостью следует, что диагонали его равны, что они образуют со сторонами квадрата равные углы, что при пересечении их образуются равные треугольники и т.д. Все эти признаки необходимо принадлежат квадрату. Но, поскольку основные определяющие признаки не выводятся из чего-либо, не ясно, какой смысл может иметь утверждение об их необходимой принадлежности квадрату. Они могут быть необходимы лишь в том смысле, что необходимо обусловленным было появление самих предметов данного качества, но это обусловленность какими-то внешними обстоятельствами, а не внутри самого предмета.

Столь же не ясно, что имеют в виду, когда говорят, что без существенных признаков предмет «не может существовать», если речь идет о предметах, уже существующих или существовавших. Если же объектом мысли является предмет, который предполагается создать, например, корабль для межпланетных путешествий, то здесь имеет смысл обсуждать вопрос не о том, без каких признаков предмет не сможет существовать, а о том, без чего он не будет соответствовать своему назначению. Но сущность предмета составляют здесь скорее не эти признаки, а, как уже говорилось, само назначение предмета. Сущность шахматного коня, например, состоит в его роли в игре, определяемой установленными для него правилами.

От введенного понятия существенности того или иного признака, в котором имеется в виду в определенной мере безотносительная существенность, то есть существенность для самого предмета, надо отличать относительную существенность. Относительно существенным является признак, который обусловливает тот или иной характер взаимодействия предмета с другими предметами, тот или иной способ его использования, например, в практической деятельности. Так, особенность воды, состоящая в том, что она имеет максимальную плотность при 4°С, существенна для нее как среды обитания водных животных. В силу именно этой особенности воды в холодное время года вода в водоемах обычно не промерзает до дна, благодаря чему на дне водоемов сохраняется жизнь обитателей водных бассейнов. В этом смысле многие признаки, не существенные для самих предметов, существенны для использования этих предметов человеком. Пластичность, гибкость меди при особенно хорошей ее электропроводности существенны при использовании ее в качестве электропроводов. При выборе артиста на некоторую роль существенны рост, фигура, а также то, является ли он брюнетом или блондином.

Результатом того, что относительно существенные признаки не отличают часто от признаков, существенных для предметов – того или иного качества – самих по себе, является распространенное в философской литературе мнение об относительности существенного и в том числе сущности вообще.

Один из наиболее видных представителей логики прагматического направления Ф. Шиллер, писал, что «сущность», которую пытается установить каждое определение, является просто пунктом, который важно выяснить для данного времени» (в связи с данной целью, ради которой рассматривается предмет). «Отсюда следует, что сущности и определения вещей являются неизбежно множественными, изменчивыми, относительными (Schiller F.I.S. Formal Logic.– London, 1912.– P. 70.)...». Так, например, по Шиллеру, нет сущности человека как таковой. Каждый может ее усмотреть в различном в зависимости от того, с какой стороны его интересует человек. «Для теолога сущностью человека является то, что он имеет душу; для врача – то, что он имеет тело; для повара – что он имеет желудок. Все эти определения закономерны... с различных точек зрения. Для существования человека одинаково существенно и то, что он делает деньги, и то, что он может любить (Там же.– P. 54.)?

За сущность предмета люди принимают обычно, по мнению Шиллера, то, что в нем больше всего бросается в глаза или является наиболее важным с точки зрения потребностей людей.

Следует иметь в виду, что в истории логики и философии слово «сущность» употреблялось и в смысле «нечто», «вещь», «предмет», «некая субстанция» (объект мысли). В этом смысле Аристотель говорил о первых и вторых сущностях. (Первая сущность – отдельная вещь. Вторичные сущности – это так называемые универсалии – нечто, обозначаемое общими именами: «лошадь», «человек», «дерево» и т.д.) Если в этом смысле про вещь говорят, что она есть некая сущность, то, понимая сущность как основу качественной специфики вещи, правомерно поставить вопрос: «Какова сущность этой сущности?», например, «Какова сущность человека?».

 

Деление признаков по месту и роли в системе признаков. Сущность предметов

До сих пор мы рассматривали виды признаков, имея в виду множество возможных признаков вообще. Однако можно говорить о множестве признаков того или иного конкретного предмета или вида некоторых предметов (металлов, жидкостей, млекопитающих). Каждый предмет мыслится, вообще говоря, как некоторая субстанция. Однако его можно для некоторых научных целей рассматривать и как систему признаков (качеств, свойств, отношений, количественных характеристик). Более строго говоря, мы всегда имеем возможность рассматривать предмет как систему (множество) известных – на данной ступени познания – признаков. Среди таких признаков предмета прежде всего различаются случайные для него и неслучайные. Случайные обусловлены некоторыми внешними обстоятельствами и ни в какой мере не определяют качественную специфику предмета. Случайными признаками металлов, например, являются наличие тех или иных примесей, та или иная их температура в определенных ситуациях. То же можно сказать о воде. Для человека случайными могут быть – особенно при командно-бюрократической организации общества – то или иное его служебное положение, окружение и т.п.

Между неслучайными признаками существуют внутренние для данных предметов связи: одни из них обусловливают другие. Их множество представляет собой таким образом некоторую систему. Для предметов некоторого вида, и тем более для отдельных конкретных предметов, это множество бесконечно. Иное дело множество признаков этого рода, познанных на том или ином этапе развития знания. Оно всегда конечно, причем в определенных случаях – при относительно завершенности процесса познания предметов на некотором этапе – это множество также представляет собой определенную систему, по крайней мере когда речь идет о признаках некоторого вида предметов (вопрос о том, в какой мере это относится к признакам отдельных предметов, является для науки пока открытым). Одни признаки здесь обусловливают другие, эти последние – третьи и т.д. В силу этих отношений субординации одни признаки системы можно охарактеризовать как более существенные, другие – как менее существенные.

Системами указанного типа являются, например, множества известных признаков металлов, жидкостей, признаков, характеризующих общественное устройство. Наличие ионной кристаллической решетки у металлов обусловливает их ковкость, пластичность; в силу наличия свободных электронов в массе металла они являются хорошими проводниками электрического тока; благодаря наличию кристаллического строения металлы, как и другие кристаллические вещества, имеют определенную температуру плавления.

Среди неслучайных признаков предметов можно выделить совокупность некоторых наиболее существенных – основных признаков, обусловливающих все остальные, общие для данных предметов. Из этой совокупности, в сочетании с известными законами соответствующей области действительности, могут быть логически выведены все известные общие для данных предметов и неслучайные для них признаки, а для абстрактных объектов – в так называемых полных теориях – вообще все признаки, общие для предметов вида.

• Совокупность основных существенных признаков того или иного вида конкретных предметов действительности называется их СУЩНОСТЬЮ.

Так, сущностью металлов, как химически простых веществ, является то, что они состоят из однородных атомов, а именно атомов с одним и тем же зарядом ядра, и атомы их обладают низким потенциалом ионизации, в силу чего легко теряют свои внешние электроны. Этим обусловлены общие для металлов химические свойства, особое строение их кристаллической решетки, хорошая электропроводность, пластичность и т.д.

Основным признаком общества (его сущностью) является господствующий в нем способ производства, характеризующийся определенным уровнем развития производительных сил и типом производственных отношений, то есть тем, что называется экономическим базисом общества. Экономический базис общества определяет характер господствующих в обществе политических взглядов, правовых отношений, идеологии, морали.

Сущность предметов некоторого качества (предметов некоторого класса), выявленная на некотором уровне познания, является основой качественной специфики этих предметов, но лишь в той мере, в какой эта специфика нам известна на данном этапе познания. Исходя из этой сущности мы можем объяснить известные общие, специфические для данных предметов (неслучайные) их признаки. В процессе дальнейшего развития знания о соответствующих предметах открываются новые качества, свойства предметов, отношения их к другим предметам, которые нельзя объяснить исходя из познанной сущности. В таком случае происходит – в результате поиска нужных объяснений – проникновение в «более глубокую» сущность предметов, открытие таких же признаков, исходя из которых могут быть объяснены все известные ранее и вновь открытые их особенности. Таким образом, существуют сущности разных уровней или порядков.

В истории философии имело широкое распространение представление о том, что у предметов того или иного вида или даже отдельных предметов имеется некоторая абсолютная сущность, основа всех его признаков. Эта «последняя сущность» должна быть, согласно этим представлениям, пределом познания соответствующих явлений. На такое понимание наводит нередко встречающееся в философской литературе определение сущности как некоторого внутреннего содержания вещи, определяющего специфику ее многообразных проявлений.

Однако исторический опыт развития знания указывает на другое, а именно на то, что сущность предмета в диалектическом ее понимании – это есть лишь тот предел, до которого дошло познание предмета на данной ступени развития знания. Познание мира, как и отдельных его областей и явлений, есть бесконечный процесс углубления знания. А это означает, что сущность может быть менее и более глубокой, и этим, в частности, объясняется смена одних теорий другими,– более высокого порядка.

Так, еще в недалеком прошлом свет в физике понимали как поток волн электромагнитного излучения определенного диапазона частоты. Но при этом не объяснялись некоторые открытые позже явления, например, явление фотоэффекта. В настоящее время господствует уже корпускулярно-волновая теория света, согласно которой свет представляет собой поток фотонов, обладающий как волновыми, так и корпускулярными свойствами.

Окисление какого-либо вещества понималось до некоторых пор как присоединение к атомам данного вещества атомов кислорода. В настоящее время этот механизм соединения атомов объясняется как результат взаимодействия внешних электронов атомов. Вообще на некотором этапе от понимания химических реакций как взаимодействий между атомами веществ произошел переход к пониманию их как взаимодействия внешних электронов и образующихся при этом ионов веществ.

Совокупность основных, существенных признаков может быть выделена также, по-видимому, в любом случае, в множестве признаков, общих для абстрактных предметов того или иного вида,– геометрических фигур, чисел, алгебраических систем и т.п. Для ромбов, например, это то, что указывается в определении фигур этого вида (и соответственно в содержании понятия ромба): плоская геометрическая фигура, замкнутая, ограниченная четырьмя сторонами, все стороны которой равны. В аксиоматической теории алгебраических систем того или иного вида (теории групп, булевой алгебры и т.д. и вообще в теории некоторой структуры, например, в геометрии, как математической, формальной теории) эту совокупность признаков (и соответственно содержание понятия рассматриваемой структуры) представляет множество аксиом. Однако эту совокупность признаков неправомерно, видимо, рассматривать как сущность структуры соответствующего вида, поскольку для одного и того же множества признаков, общих для структур некоторого вида, существует, вообще говоря, не одна такая совокупность. Так вместо указанной совокупности, основных существенных признаков ромба может быть другая, получающаяся из нее заменой признака «равносторонняя фигура» на «фигура, диагонали которой взаимно перпендикулярны и в точке пересечения делятся пополам». Известно также, что существуют эквивалентные теории с различными составами аксиом. Неестественно, конечно, было бы считать, что объекты одного и того же типа имеют на одном и том же уровне познания различные сущности.

Специфическими являются случаи, когда дело касается предметов, созданных людьми для тех или иных определенных целей. Обычно сущность такого рода предметов усматривают именно в их назначении, что отражается в определениях. Часы – это прибор, с помощью которого можно отсчитывать время; термометр – прибор, служащий для измерения температуры, и т.д. Назначением предмета определяются и все его другие качества. Это и служит причиной того, что оно принимается за сущность. Хотя верно и другое: благодаря наличию определенных качеств (особому устройству) та или иная вещь выполняет определенные функции. Качества вещи, предназначенной для определенной цели, вытекают из ее назначения логически. Способность же вещи служить определенной цели обусловлена ее качеством фактически, как действие – причиной. Но поскольку человек мысленно конструирует вещь прежде, чем создает ее, и при этом выводит все ее качества именно из предназначения вещи, то это последнее оказывается решающим. Здесь, как видим, сущность вещей определяется практическими потребностями людей. Но это не указывает на субъективный характер данного понятия, поскольку сами вещи, которые здесь имеются в виду, создаются людьми именно для удовлетворения своих потребностей.

В любом случае основные существенные признаки предметов некоторого вида составляют основу их качественной специфики, поскольку они обусловливают все другие общие и, в совокупности, специфические для данных предметов признаки. В случае конкретных предметов действительности обусловленность имеет причинный или целевой характер, в случае абстрактных объектов – структурный или функциональный характер. Но в том и другом случае из совокупности указанных основных признаков в сочетании с законами данной области действительности все другие неслучайные признаки предметов выводимы логически.

Сущность предметов того или иного вида составляют обычно признаки, недоступные наблюдению. Они выявляются теоретическим способом именно в результате построения и обоснования теории, объясняющей известные признаки изучаемых предметов. Кстати, именно в процессе построения такой теории прежде всего происходит отделение неслучайных признаков от случайных. Случайные выделяются тем, что не поддаются объяснению и не вписываются в возникающую при построении теории систему.

Еще в XVIII веке возник, например, вопрос о сущности воды. Речь шла именно о том, как объяснить известные в то время общие для всех случаев существования воды ее свойства. Основой обобщения всех этих случаев под общим названием – именем «вода» – являлось первоначально практическое использование воды и связанная с этим обобщением интуиция. Как обычно при построении теории возникло несколько гипотез. Одна из них, которая затем получила теоретическое и экспериментальное подтверждение и стала общепризнанной,– гипотеза Лавуазье о том, что вода есть химическое соединение кислорода и водорода. Экспериментальным подтверждением оказалось получение воды из «гремучего газа». При этом как раз выяснилось, что наблюдаемые в различных случаях примеси воды не связаны с ее сущностью, то есть представляют собой случайные признаки. Углублением знания сущности воды, указанной Лавуазье, стало в дальнейшем понимание того, что вода есть химически сложное вещество, молекулы которого состоят из двух атомов водорода и одного атома кислорода. При этом удалось объяснить и такое примечательное свойство воды, как сжатие ее при нагревании от 0°С до 4°С, обусловленное перестройкой молекулярной структуры воды в этом температурном промежутке.

Итак, в системе познанных признаков некоторого вида выделяются: 1) основные, существенные признаки для конкретных предметов действительности, составляющие их сущность; 2) производные – обусловленные основными, а также 3) случайные признаки. Явно несостоятельным является также определение в философской и логической литературе сущности предмета как того, что необходимо принадлежит предмету, без чего он не может существовать, не может быть тем, что он есть. Попытка применить его практически обнаруживает даже, что оно содержит скрытый круг. Попробуем, например, руководствуясь им, выделить существенные признаки квадрата. Для этого нужно установить, без каких признаков ту или иную фигуру нельзя отнести к квадратам. Но это уже требует знания существенных признаков квадрата. Мы не назвали бы квадратом, например, четырехугольник, углы которого не являются прямыми, а стороны равными, но именно потому, что знаем, что эти признаки являются существенными для квадрата.

Вообще, для решения вопроса о том, без каких признаков предмет не был бы тем, что он есть, надо знать, чем именно этот предмет является, какими существенными признаками выделяется из числа других предметов.

Если сущность предмета выявлена, то оказывается, что одни признаки необходимо принадлежат ему, потому что вытекают из сущности, другие являются случайными, потому что не связаны с нею. Из определения квадрата как прямоугольного и равностороннего четырехугольника с необходимостью следует, что диагонали его равны, что они образуют со сторонами квадрата равные углы, что при пересечении их образуются равные треугольники и т.д. Все эти признаки необходимо принадлежат квадрату. Но, поскольку основные определяющие признаки не выводятся из чего-либо, не ясно, какой смысл может иметь утверждение об их необходимой принадлежности квадрату. Они могут быть необходимы лишь в том смысле, что необходимо обусловленным было появление самих предметов данного качества, но это обусловленность какими-то внешними обстоятельствами, а не внутри самого предмета.

Столь же не ясно, что имеют в виду, когда говорят, что без существенных признаков предмет «не может существовать», если речь идет о предметах, уже существующих или существовавших. Если же объектом мысли является предмет, который предполагается создать, например, корабль для межпланетных путешествий, то здесь имеет смысл обсуждать вопрос не о том, без каких признаков предмет не сможет существовать, а о том, без чего он не будет соответствовать своему назначению. Но сущность предмета составляют здесь скорее не эти признаки, а, как уже говорилось, само назначение предмета. Сущность шахматного коня, например, состоит в его роли в игре, определяемой установленными для него правилами.

От введенного понятия существенности того или иного признака, в котором имеется в виду в определенной мере безотносительная существенность, то есть существенность для самого предмета, надо отличать относительную существенность. Относительно существенным является признак, который обусловливает тот или иной характер взаимодействия предмета с другими предметами, тот или иной способ его использования, например, в практической деятельности. Так, особенность воды, состоящая в том, что она имеет максимальную плотность при 4°С, существенна для нее как среды обитания водных животных. В силу именно этой особенности воды в холодное время года вода в водоемах обычно не промерзает до дна, благодаря чему на дне водоемов сохраняется жизнь обитателей водных бассейнов. В этом смысле многие признаки, не существенные для самих предметов, существенны для использования этих предметов человеком. Пластичность, гибкость меди при особенно хорошей ее электропроводности существенны при использовании ее в качестве электропроводов. При выборе артиста на некоторую роль существенны рост, фигура, а также то, является ли он брюнетом или блондином.

Результатом того, что относительно существенные признаки не отличают часто от признаков, существенных для предметов – того или иного качества – самих по себе, является распространенное в философской литературе мнение об относительности существенного и в том числе сущности вообще.

Один из наиболее видных представителей логики прагматического направления Ф. Шиллер, писал, что «сущность», которую пытается установить каждое определение, является просто пунктом, который важно выяснить для данного времени» (в связи с данной целью, ради которой рассматривается предмет). «Отсюда следует, что сущности и определения вещей являются неизбежно множественными, изменчивыми, относительными (Schiller F.I.S. Formal Logic.– London, 1912.– P. 70.)...». Так, например, по Шиллеру, нет сущности человека как таковой. Каждый может ее усмотреть в различном в зависимости от того, с какой стороны его интересует человек. «Для теолога сущностью человека является то, что он имеет душу; для врача – то, что он имеет тело; для повара – что он имеет желудок. Все эти определения закономерны... с различных точек зрения. Для существования человека одинаково существенно и то, что он делает деньги, и то, что он может любить (Там же.– P. 54.)?

За сущность предмета люди принимают обычно, по мнению Шиллера, то, что в нем больше всего бросается в глаза или является наиболее важным с точки зрения потребностей людей.

Следует иметь в виду, что в истории логики и философии слово «сущность» употреблялось и в смысле «нечто», «вещь», «предмет», «некая субстанция» (объект мысли). В этом смысле Аристотель говорил о первых и вторых сущностях. (Первая сущность – отдельная вещь. Вторичные сущности – это так называемые универсалии – нечто, обозначаемое общими именами: «лошадь», «человек», «дерево» и т.д.) Если в этом смысле про вещь говорят, что она есть некая сущность, то, понимая сущность как основу качественной специфики вещи, правомерно поставить вопрос: «Какова сущность этой сущности?», например, «Какова сущность человека?».

ПОНЯТИЕ КАК ФОРМА МЫШЛЕНИЯ

§ 15. Понятие как форма мышления. Общая характеристика

Понятие обычно определяют как одну из основных форм мышления; этим подчеркивается важная роль его в познании. Переход от чувственной ступени познания к абстрактному мышлению характеризуется прежде всего как переход от отражения мира в формах ощущений, восприятий и представлений к отражению его в понятиях и на их основе в суждениях и теориях. Мышление, таким образом, может рассматриваться как процесс оперирования понятиями. Именно благодаря понятиям мышление приобретает характер обобщенного отражения действительности.

Мышление, а именно абстрактное мышление, как мы уже определили,– это отражение действительности посредством языка. Наиболее существенным моментом, определяющим возможность познания действительности с помощью языка, является обобщение предметов некоторого класса, вида (например, животных, растений, металлов и т.д.) и мысленное выделение их при этом. Результатам таких обобщений, по крайней мере, в нетривиальных случаях (когда предметы не могут быть отображены в чувственных образах) являются именно понятия. Более того, применение понятий в мышлении необходимо всегда, когда к мышлению предъявляются требования определенности, точности и особенно доказательности. Специфика этой формы мышления состоит в том, что она прежде всего представляет собой результат мысленного и, значит, словесно-языкового выделения предметов некоторого класса, то есть предметов, качественно сходных в каком-то отношении. Выделение осуществляется по определенной совокупности признаков, отличительной для данных предметов, такой, что все признаки данной совокупности вместе достаточны, чтобы отличить эти предметы от всех остальных. Это означает, что каждый признак из этой совокупности необходим для выделения данного класса. Для выделения, например, класса студентов используются признаки: «человек», «учащийся», притом «учащийся высшего или среднего специального гражданского учебного заведения». Аналогично «материальный предмет, который в процессах мышления и общения людей является представителем каких-либо других объектов» (знак), «целое положительное число, отличное от единицы и имеющее ровно два различных делителя» (простое число) и т.п. Но, для того чтобы выделить класс предметов по какой-то совокупности признаков, необходимо обобщить данные предметы по этим признакам. Обобщение состоит в том, что мы отвлекаемся от всех индивидуальных и иных различий внутри класса, от того, например, что есть студенты технических и гуманитарных вузов, есть хорошо и плохо успевающие и т.п. В результате предметы мыслятся абстрактно: только как обладающие указанной отличительной совокупностью признаков. Таким образом, мы имеем мысленное образование: «Человек, являющийся учащимся высшего или среднего специального гражданского учебного заведения».

В силу обобщенного характера отражения предметов в понятии они мыслятся в понятии всегда в той или иной мере абстрактно. Но это не означает, как часто представляется, что сами мыслимые в них предметы всегда суть некоторые абстракции и что именно эти абстракции, а не конкретные предметы действительности являются объектом изучения науки. Верно, что в каждом понятии мы мыслим те или иные предметы в той или иной мере абстрактно, но используем понятия для утверждения о конкретных, обобщенных в них предметах. В понятиях: «металл», «растения», «атомы» и т.п.– имеются в виду в качестве элементов объема некоторые предметы действительности. Когда мы утверждаем, что все студенты обязаны сдавать экзамены, то, конечно, относим эту обязанность к конкретным людям, а не к неким абстрактным объектам. Лишь в некоторых случаях предметами понятий являются те или иные идеализированные предметы действительности («абсолютно упругая жидкость», «идеальный газ», «материальная точка» и т.п.); идеальные предметы («земной меридиан», «сила»), абстрактные объекты (характеристики реальных предметов или множеств предметов, отвлеченные от них и ставшие самостоятельными объектами мысли, результаты изолирующего абстрагирования – пространство, время, упругость, числа, геометрические фигуры и т.п.) и, конечно,– в соответствии с широким пониманием термина «предмет» – предметами понятия, элементами его объема могут быть также и явления, события, процессы (восход солнца, революция, перестройка, механическое движение и т.п.).

Подводя итог изложенному, можно сказать, что понятие как форма (вид) мысли, или как мысленное образование, есть результат обобщения предметов некоторого вида и мысленного выделения соответствующего класса (множества) по определенной совокупности общих для предметов этого класса – ивсовокупности отличительных для них – признаков.

Характеристика понятия как формы познания, как способа мыслительной деятельности явствует из данного определения. Это – способ мысленного выделения классов предметов посредством обобщения этих предметов. Этот процесс включает, как правило, более или менее широкое множество приемов познания. Наибольшую ценность в познании представляют собой понятия, в которых предметы обобщаются по существенным признакам. Однако с гносеологической точки зрения мысль представляет собой понятие независимо от того, насколько существенными являются признаки, составляющие основу обобщения предметов, тем более, что для предметов одного и того же класса возможны, как мы уже говорили, и менее» и более существенные признаки, существенные для характеристики самих этих предметов или с какой-то точки зрения в связи с тем или иным использованием предметов (см. § 14).

Понятие в строгом и не в строгом смысле. В гл. II отмечалось, что общие (как и единичные) имена употребляются интуитивно более или менее точно и без осознания того, по каким именно признакам выделяются или могут быть выделены обозначаемые ими предметы. В этом случае не выявлен смысл соответствующих общих имен, а следовательно, строго говоря, они не выражают понятий. Так, человек может пользоваться словами «дерево», «человек», «болезнь», не умея отвечать на вопрос, что именно он имеет в виду, какие признаки специфичны для мыслимых здесь предметов. В одних случаях подобного рода со словами связываются лишь некоторые более или менее четкие представления (чувственные интуиции) и через посредство именно этих представлений осуществляется связь слов с предметами действительности. В других – некоторые интеллектуальные интуиции, возникшие в процессе усвоения языка. Первоначальной основой указанных интуитивных связей имен с обозначаемыми ими предметами является совместная практическая деятельность людей и, конечно, общение их в процессе деятельности. Люди выделяют предметы некоторых классов и дают им общие названия благодаря способности этих предметов удовлетворять их определенные потребности.

В практике научного познания понятиями называют и те абстракции, которые представляют интуитивно употребляемые имена. Таким образом, термин «понятие» употребляется в более широком, чем указано выше, смысле. Так, говорят, например, «дерево» – это понятие, «человек» – это понятие, независимо от того, связываются или нет с этими словами знания о том, что представляют собой обозначаемые ими предметы, выделены ли в этих предметах те признаки, которые составляют основу их обобщения, или же имеются лишь более или менее ясные, нерасчлененные интуиции.

Иначе говоря, понятием в этом значении термина называют просто любой предмет, ставший объектом мысли (следовательно, названный и мыслимый в той или иной степени абстрактности). Часто в философии прошлого, для этого употреблялся термин «идея». Например, Д. Локк, используя этот термин, указывает, что под ним подразумевается «все, что является объектом мышления человека (Локк Д. Избранные философские произведения: В 2 т.– М., 1960.– Т. 1.– С. 75.)». Оперируя таким понятием, человек может не иметь о нем понятия. Это парадоксальное, на первый взгляд утверждение означает лишь то, что дважды употребленный в этой фразе термин «понятие» имеет в одном и другом случаях разные значения. Так, А.И. Герцен в письме «Эмпирия и идеализм» говорит о существовании в науках понятий, которые еще не понятны (Герцен А.И. Избранные философские произведения.– М., 1948.– С. 93.). Однако во всех случаях, где необходимо точное понимание смыслов утверждений, и особенно если возникает надобность в доказательствах наших высказываний, мы не можем ограничиваться интуициями. В подобных ситуациях необходимы понятия в строгом смысле этого слова, которых мы и будем придерживаться.

 Логическая структура и основные характеристики понятия

Совокупность признаков, по которым обобщаются предметы в понятии, называется содержанием данного понятия, точнее было бы сказать основным содержанием. Далее, мы будем различать основное и полное содержание понятия и в связи с этим различать само понятие просто как охарактеризованное выше обобщение предметов, то есть как смысл общего имени и как некоторую систему знаний. При корректном способе образования понятия основное содержание его – это совокупность признаков, которые все вместе достаточны, а каждый необходим для того, чтобы выделить данный класс предметов, то есть отличить эти предметы от других. Например, добавление перпендикулярности диагонали к содержанию указанного понятия квадрата делает совокупность избыточной; данный признак является производным – выводимым из основного содержания понятия квадрата. Класс обобщаемых в понятии предметов называется его объемом. Мыслимые (обобщаемые в понятии) предметы – носители признаков, составляющих содержание понятия,– суть элементы объема этого понятия. Части объема – это виды предметов, обобщенных в понятии, и выделение их означает выявление определенных различий внутри класса предметов. Обобщая предметы в понятиях, как было сказано, мы отвлекаемся от всяких различий внутри соответствующего класса предметов. Но когда понятие образовано, возникает обычно необходимость выявления их уже на основе полученного обобщения. Это выявление осуществляется в форме особой операции, называемой делением понятия, и представляет собой определенную конкретизацию данного понятия.

 

¹ « ≡ » – знак равносильности.

 

Выше была указана совокупность признаков, составляющая содержание понятия «студент». Объем этого понятия есть класс всех людей, обладающих этими признаками, то есть класс всех тех, кого мы называем студентами. Отдельные люди этого множества – элементы его объема. Частями объема являются, например, множество студентов технических вузов, а также гуманитарных, множество студентов выпускников и начинающих обучение и т.д. Следует обратить внимание на то, что объем понятия в отличие от содержания понятия не является частью понятия как мысли. Он представляет собой класс реально или, по крайней мере, независимо от понятия существующих объектов. Указание на объем понятия при его характеристике есть указание именно на то, к чему относится данное понятие, на то, что обобщается в нем.

Для понимания структуры понятия существенно учитывать, что выделение мыслимого в нем множества предметов осуществляется всегда в пределах некоторого более широкого класса. Интересующие нас предметы мы мыслим в понятии как вид предметов некоторого рода, как нечто особенное в пределах чего-то общего. Так, треугольники мыслятся как вид плоских геометрических фигур; механическое движение – как вид изменения (именно изменение положения тела в пространстве), деревья – как вид растений; хозрасчет – как вид способов (методов) ведения хозяйства и т.д. В соответствии с этим среди признаков, составляющих содержание понятия, выделяются родовые и те, что составляют видовые отличия мыслимых в понятии предметов. Так, например, в формулировке понятия квадрата: «Четырехугольник с прямыми углами и равными сторонами» или более развернуто: «Плоская, замкнутая, ограниченная четырьмя равными сторонами фигура, все стороны которой равны и углы прямые» – слова «плоская, замкнутая, ограниченная четырьмя сторонами фигура» указывают родовые признаки понятия, а «прямоугольность» и «равносторонность» составляют видимое отличие «квадрата», именно то, что выделяет квадраты в множестве четырехугольных геометрических фигур. Род понятия составляет субстанционная часть, а видовое отличие – его атрибутивная часть.

Вместе с тем указанное разделение признаков на родовые и видовые не является абсолютным. В зависимости от задач, с которыми связано образование понятия, в качестве рода может быть взят один или другой, более широкий класс. Те же квадраты мы можем мыслить и как вид четырехугольников, и как вид замкнутых плоских геометрических фигур, относя «четырехугольность» в таком случае к видовому их отличию, а также вид геометрических фигур вообще. В каждом из указанных случаев мы получим различные понятия об одних и тех же предметах, более того, возможно обобщение одних и тех же предметов в различных понятиях по различным совокупностям признаков вообще. Металлы, например, можно мыслить как химически простые вещества с особой, ионной, кристаллической решеткой или как химически простые вещества, атомы которых обладают низким коэффициентом ионизации. Один и тот же класс треугольников может быть обобщен в понятиях «равносторонний треугольник» и «равноугольный треугольник».

Надо иметь также в виду, что элементами объема понятия могут быть отдельные предметы (индивиды) и некоторые системы объектов: пары, тройки и т.д. Например, в понятиях «изотопы», «братья», «родственники» мыслятся некоторые пары этих предметов, обобщаемые по признакам, представляющим собой двухместное отношение: «изотоп», «брат», «родственник» и т.д. Вообще, элементами объема понятия могут быть системы, представляющие собой некоторые множества предметов с заданными на них отношениями (в математике называемых структурами). Таковы, например, группы, составляющие предмет теории групп, решетки, булевы алгебры и т.д.

Необходимо заметить также, что совокупность признаков, составляющих видовое отличие понятия, можно и полезно мыслить как некоторый один признак, объединяющий все признаки в конъюнкцию. В таком случае видовое отличие представляется в виде некоторого предиката – либо одноместного, либо многоместного,– в зависимости от того, являются ли элементами объема понятия индивиды или системы предметов.

Учитывая это, для выражения видовых отличий понятий можно использовать язык логики предикатов. Если при этом видовое отличие представляет одноместный предикат А(х), то структура понятия может быть представлена в виде хА(х).

Родовые признаки понятия в таком случае составляют характеристику области D – возможных значений переменной х, а все выражение «хА(х)» означает: «предмет хиз области D такой, что он обладает признаком А(х)». Например, «плоская геометрическая фигура, замкнутая, ограниченная четырьмя сторонами, имеющая равные стороны и прямые углы» (квадрат) можно представить в виде: хА(х), где область х – множество плоских геометрических фигур, а А(х) есть конъюнкция признаков: замкнутая, ограниченная четырьмя сторонами, имеющая равные стороны и прямые углы.

Понятие «изотопы» будет нами представлено в виде: (х, у) А(х, у). Область х и у – химические элементы, а А(х, у) означает: заряд ядра атома х равен заряду ядра у. С лингвистической точки зрения выражение хА(х), как и (х, у) А(х, у) и (х, у, z) А (х, у, z), представляют собой описательные общие имена. На их основе могут быть образованы единичные описательные имена с использованием оператора «?» («тот ..., который ...»): если объем понятия хА(х) является единичным классом, то правомерно образовать единичное имя – ?хА(х) (тот предмет х из области D, который обладает свойством A(x)). Например, из общего понятия «небесное тело (D),вращающееся вокруг Солнца и являющееся ближайшим к Солнцу (А(х))» образуем: «то небесное тело, которое вращается вокруг Солнца и является ближайшим к нему». Это описательное единичное имя планеты Меркурий. Смысл единичного описательного имени ?хА(х) – это своеобразное понятие, которое в отличие от общего понятияхА(х) содержит дополнительную информацию о мыслимом предмете, о том, что этот предмет является единственным обладателем свойства А(х). Такие понятия принято называть индивидными концептами.

 

Упражнения

 

1. Проанализируйте следующие понятия (укажите содержание, объем, какие-нибудь элементы и части – если можно выделить таковые – объема, выделите родовые признаки и признаки, составляющие видовое отличие):

а) слово, обозначающее какое-нибудь действие или состояние;

б) самый большой город Кубы;

в) город, который является столицей какого-нибудь государства;

г) город, который является столицей Китая.

2. Укажите, из каких вышеприведенных понятий можно (осмысленным образом) образовать описательные единичные имена. Образуйте такие имена.

3. Сформулируйте какие-нибудь понятия, относящиеся к физике, химии, географии, истории, литературе, и осуществите их анализ.

 

Слово и понятие. Понятие и представление

Как и всякая мысль, понятие выражается в определенной знаковой форме. Непосредственно такими формами в естественном языке являются общие описательные имена. Обычно вместо них используются всякого рода сокращения («студент», «треугольник»). Понятия составляют смысл имен такого рода и в силу указанной их функции – мысленного выделения предметов – связывают эти имена с теми объектами, которые они должны представлять как знаки языка в процессах коммуникации и мышления.

Напомним, что смысл является категорией семиотики, конкретнее – семантики, и представляет собой одну из характеристик знаков. Говоря о понятии, мы выходим за пределы теории знаков, рассматривая понятие не как некоторую характеристику знаков, а как определенную форму отражения действительности на ступени абстрактного мышления, то есть на ступени познания действительности с помощью языка. То, что в семантике называется смыслами знаков, представляет собой определенные мысленные образования, результаты определенной мысленной переработки предметов действительности и фиксации их в языке. В этих образованиях, как увидим далее, весьма различных по своим структурам, находит выражение своеобразие и многообразие форм мыслительной, познавательной деятельности человека. В связи с вопросом о соотношении знаковой формы понятия и сокращающих слов следует различать два типа ситуаций.

1. В процессе той или иной научной деятельности или в повседневной жизни человек вводит некоторые понятия, выделяя интересующий его класс предметов, и затем подбирает какое-нибудь сокращающее слово – общее имя для этих предметов.

2. Имеется уже более или менее точно интуитивно употребляемое в научном или повседневном обиходе некоторое имя, обозначающее предметы некоторого класса, и затем образуется понятие о соответствующих предметах, отвечающее на вопрос, что представляют собой эти предметы. (Операцию такого рода называют «реальным» определением термина.)

В первом случае понятие может быть сформулировано на основе нескольких или даже единичного наблюдаемого случая. Так, обнаружение вначале лишь одного химически простого вещества – радия – с самораспадающимися атомами послужило основанием для создания общего понятия «радиоактивное вещество».

Возможно даже, и часто это происходит в фундаментальной науке, образование понятий о предметах, существование которых только предполагается или допускается как возможное. На основе знания, например, того, что атомы известных химически простых веществ состоят из положительно заряженного ядра и вращающихся вокруг него отрицательных частиц – электронов, ученые предположили возможность существования частиц, устроенных «наоборот», а именно состоящих из отрицательно заряженного ядра и вращающихся вокруг него положительно заряженных частиц – позитронов. Так возникло общее понятие антиатома.

Ясно, что объем образованного таким образом понятия может оказаться пустым. Впрочем, в науке вводятся и используются для определенных целей понятия и с пустыми объемами: например, понятие «вечный двигатель» (и даже вечный двигатель первого рода и второго рода). Оно применяется для формулировки определенных законов термодинамики, а именно как раз для утверждения о невозможности вечного двигателя (как первого, так и второго рода).

Как правило, понятие является результатом сложного процесса мыслительной деятельности. В случаях же второго типа дело осложняется часто еще недостаточной четкостью предметных значений употребляемых слов, как знаков. Процесс образования понятий здесь сочетается обычно с уточнением этого значения путем просмотра того, в каких именно контекстах (или, как бы сказал Витгенштейн, по каким правилам) употребляется слово в данном сообществе. Как правило, при этом выявляется даже многозначность употребления того или иного слова, например, слова «игра» как обозначение имитации некоторой деятельности ради удовольствия – детские игры, или отработки приемов некой деятельности, или состязаний, или действий актеров и т.д. И довольно неясно до сих пор, возможно ли некоторое обобщение, по существу, всех этих отдельных ситуаций в едином понятии. Аналогичным образом дело обстоит со словом «болезнь» и многими другими.

Понятие и представление. Как уже отмечалось, обобщаемые в понятиях предметы первоначально могут быть даны в представлениях. Для класса чувственно воспринимаемых предметов возможны даже некоторые общие представления, некоторые «усредненные» образы этих предметов (например, можно иметь некоторый «недетализированный» образ дерева, человека). Однако едва ли возможны подобные способы воспроизведения в сознании таких предметов, как растения, организмы, и тем более объектов, не относящихся к чувственно воспринимаемым («искривленное пространство», «свет», «электромагнитное поле» и т.п.).

С одной стороны, представления ближе к действительности, предметы отражаются в них в более или менее цельном, естественном виде. Понятие представляет собой в некотором роде схематическое, но, как правило, более глубокое отображение предметов. Отображение действительности в понятиях обеспечивает неограниченные возможности познания действительности. Существенно в этом отношении то, что представления субъективны, а понятия и силу их фиксации в языке интерсубъективны. Представление более или менее конкретно, понятие абстрактно.

Однако и оперирование понятиями в той или иной мере связано с представлениями. Расчленяя в понятии предметы и явления на признаки, мы связываем, в свою очередь, обычно сами эти признаки с некоторыми представлениями. И даже имея дело с сугубо абстрактными предметами, человек стремится ввести в свои рассуждения элементы наглядности, конструируя для этой цели некоторые представления – наглядные модели абстрактных объектов.

Основные приемы образования понятий. Значение понятий в познании

Понятия – это результат более или менее сложной мыслительной деятельности. В этой деятельности можно выделить следующие наиболее важные и общие приемы.

Анализ предметов, данных в представлении,– разложение их на отдельные признаки, выявление их связей и отношений с другими предметами. Синтез – воспроизведение предметов, расчлененных в процессе анализа на отдельные признаки, представляющее их как систему выделенных свойств и отношений. Сравнение – выявление сходств и различий между предметами. Обобщение – объединение в одной мысли под одной знаковой формой множества предметов по сходным их чертам. Обобщение связано, как уже было замечено, с процессом абстрагирования.

Полезно напомнить читателю три вида абстрагирования. Один из них состоит в том, что в предмете выделяются какие-то признаки, а все другие остаются за пределами внимания. Другими словами, происходит отвлечение от всех других признаков. Результат применения такого приема есть абстрактно мыслимый, характеризуемый лишь некоторой совокупностью выделенных признаков предмет. Именно этот прием неразрывно связан с обобщением предметов некоторого класса и поэтому может быть назван обобщающе-различающим абстрагированием.

Второй вид – отождествляющее абстрагирование. Прием состоит в том, что, выделяя некоторые признаки предмета, мы игнорируем все остальные как несущественные с той или иной точки зрения. Это ведет к отождествлению всех предметов, обладающих выделенными признаками. Таким образом, например, выделяя те или иные слова по их структуре, мы игнорируем все различия, связанные с их написанием или произношением, и рассматриваем все случаи употребления слова одной и той же структуры как различные экземпляры одного и того же слова.

И наконец, имеется так называемое изолирующее абстрагирование, состоящее в том, что отдельные признаки предметов, отдельные их характеристики мысленно отделяются от самих предметов и становятся самостоятельными предметами мысли. Результатом таких процессов являются так называемые абстрактные объекты и понятия: «фигура», «качество», «количество», «талант», «объем», «длина» и пр.

Следует различать (часто смешиваемые) такие приемы познания, как обобщающее абстрагирование и идеализация. Идеализация состоит в том, что, имея в виду некоторые предельные случаи (предел уменьшения трения, увеличение упругости и т.д.), мы либо мысленно наделяем предметы какими-то свойствами, которых они в действительности не имеют (например, физические тела – способностью восстанавливать при деформации свой объем или форму, в результате чего появляются понятия типа «идеально упругое тело» или «идеальная жидкость»), либо лишаем их каких-то свойств, которыми они в действительности обладают. Так возникают в нашем сознании «безразмерные» точки, линии, лишенные ширины, «идеальный газ» (молекулы которого при соударениях ведут себя как абсолютно упругие шарики). Обобщенно говорят, что понятие является результатом анализа мыслимых в нем предметов.

• Итак, в понятии выделяются некоторые классы предметов посредством обобщения этих предметов. Результаты таких выделений в понятиях представляют определенные «узлы» в познаний, вокруг которых концентрируются все наши знания.

Так в процессе познания мы постоянно накапливаем знания о животных и растениях (и различных видах тех и других), о металлах и металлоидах, об энергии и механическом движении, о государстве и классовой борьбе, о теплоте, электричестве, магнетизме и т.д., имея каждый раз в основе той или иной системы знаний определенные понятия. Существенную роль играют понятия в формулировке законов науки, которые представляют собой, как известно, общие утверждения, относящиеся к тем или иным класса предметов, обобщенных в понятиях. «Во всякой замкнутой системе энтропия возрастает» – это предложение имеет определенный смысл и только в этом случае может быть истолковано как выражение закона природы, если определенный смысл имеют его части: «замкнутая система», «энтропия», «возрастает». Эти смыслы суть понятия.

Представляя собой смыслы общих имен и имея таким образом в качестве своих знаковых форм описательные общие имена, понятия по своим знаковым формам являются своеобразными переменными естественного языка, для которых мы употребляем название «специфицированные переменные». Именно благодаря понятиям абстрактное мышление характеризуется как обобщенное отражение действительности. Всякий отдельный предмет, явление и т.д. познается здесь на основе некоторого общего понятия, как отдельное в чем-то общем (медь – как металл со своими особыми характеристиками; исторический роман – на основе понятия литературного произведения вообще).

Более того, понятия нужны не только для формулировок и объяснения законов, знание которых является результатом эмпирических обобщений (в частности, посредством популярной индукции). Для того чтобы объяснить, например, почему давление газа на стенки сосуда увеличивается с уменьшением его объема и с повышением температуры, надо иметь понятия, выражающие сущности самого газа, давления, температуры. Необходимо осознать, что газ представляет собой совокупность хаотически движущихся молекул, что давление на определенную единицу площади сосуда есть совокупная сила ударов молекул о соответствующий участок стенок сосуда и что температура газа – это показатель средней кинетической энергии движения молекул, от которой и зависит сила ударов молекул о стенки сосуда.

 

Закон обратного отношения между объемами и содержаниями понятий. Логические и фактические объемы и содержания понятий

Мы видели, что наряду с определением содержания понятия как совокупности признаков, возможна характеристика его как некоторого предиката. Поскольку предикат представляет собой высказывательную форму, он выражает некоторую информацию о предметах, мыслимых в понятии. В силу этого представление содержания как предиката позволяет истолковать его как характеристику информативности понятия. Различение понятий по информативности существенно для выяснения многих аспектов при анализе этой формы мышления. Оно приводит, в частности, к устранению многих недоразумений, которые возникали в прошлом, в частности, в связи с известным в логике законом обратного отношения между объемами и содержаниями понятий. В распространенной формулировке он гласит: объем и содержание понятия находятся в обратном отношении: чем шире объем, тем уже содержание понятия, и наоборот. Более точно, имеется в виду отношение между объемами и содержаниями двух понятий хА(х) и хВ(х) с одним и тем же родом (область значений х – D). Согласно закону, если объем одного из этих понятий шире объема другого, то содержания их находятся в обратном отношении.

Может быть принята и более общая формулировка:

• Если объем одного понятия составляет часть объема другого (с тем же родом), то содержание второго составляет часть содержания первого.

Кроме того, поскольку понятия имеют один и тот же род, отношение «часть – целое» между содержаниями понятий сводится к отношению между видовыми отличиями этих понятий, то есть между предикатами А(х) и В(х).

Таким образом приходим к формулировке:

• Объем одного понятия составляет часть другого (с тем же родом), если и только если содержание второго составляет часть содержания первого.

Однако, если для объемов понятий мы уже имеем определение отношения «объем одного понятия составляет часть объема другого» (см. § 16), то аналогичное отношение для содержаний понятий определить не так просто. Первое, что напрашивается, это – сравнение содержаний понятий по количеству признаков. В таком случае для понятий «число, которое делится на 2 и на 3» и «число, которое делится на 3» вопрос решается просто: содержание первого шире, поскольку больше количество составляющих его признаков. Однако сразу возникает неясность, когда мы рассматриваем понятия «число, которое делится на 2 или на 3» и «число, которое делится на 3». Кажется, что количество признаков в первом также больше, чем во втором, но объем первого также шире, чем объем второго. В таких понятиях как «студент, сдавший все экзамены сессии на отлично» и «студент, сдавший какие-нибудь экзамены сессии на отлично» количество признаков представляется даже одинаковым. Однако они явно различаются по своей информативности. «Сдал все экзамены» безусловно более информативно, чем «сдал некоторые экзамены», и ясно, что объем первого понятия уже, чем объем второго. Ясно также, что «делится на 3» содержит больше информации, чем «делится на 2 или на 3». Кстати, «делится на 2 или на 3» – это один признак, он является общим для чисел, обобщаемых в приведенном выше понятии (сравни «слово, обозначающее действие или состояние» среди приведенных выше упражнений).

В истории логики известен так называемый парадокс Больцано, по видимости, опровергающий закон обратного отношения. Формулируются два понятия: «Человек, знающий европейские языки» (имеются в виду, конечно, все европейские языки) и «Человек, знающий живые европейские языки». Видимость такова, что содержание второго понятия шире, поскольку к характеристике языков добавляется признак «живые», то есть действующие в настоящее время. Но и объем этого понятия также шире, чем объем первого. Ясно, что всякий, знающий все европейские языки, знает конечно, и все живые европейские языки, но не наоборот. Отношения между объемами этих понятий может быть представлено схемой:

 

 

А – человек, знающий все живые европейские языки

В – человек, знающий все европейские языки

Из этой схемы очевидно, что людей, знающих все живые европейские языки, больше, чем людей, знающих все эти языки.

Для сравнения признаков по информативности может быть использовано понятие «логическое следование». Если из высказывания или высказывательной формы А логически следует В, то есть А ╞ В, но обратное неверно, тогда А более информативно, чем В. A ╞ В само по себе указывает на то, что информация В составляет часть информации А. Обозначим объемы понятий хА(х) и хВ(х) соответственно WxA(x) и WxB(x) («WxA(x)» читается: множество предметов х, обладающих свойством А(х)). Тогда закон обратного отношения для двух понятий принимает вид:  если и только если А(х) ╞ В(х).

 

 

Видовое отличие второго понятия выражает предикат «Для всякого европейского языка, если он является живым, то х знает его» –  Нетрудно убедиться – и предлагаем это читателю,– что из первого логически следует второе: 

Однако приведенных уточнений все-таки оказывается недостаточно. Возьмем, например, пары понятий «квадрат» и «квадрат с взаимно перпендикулярными диагоналями», или «число, делящееся на 2 и на 3» и «число, делящееся на 2, на 3 и на 6». Согласно понятию логического следования и введенному определению отношения «часть» для содержаний между понятиями, содержание второго понятия в каждой из этих пар шире, чем содержание первого, однако объемы первого и второго в каждой паре совпадают. Для разрешения трудностей этого рода необходимы определенные уточнения понятий «содержание понятия», «объем понятия», а вместе с тем и формулировки самого закона. Необходимо различать логическое и фактическое содержание понятия и аналогично логический и фактический объемы понятий. Логическое содержание, которое до сих пор, по существу, имелось в виду,– это имеющаяся в понятии информация относительно обобщаемых в нем предметов, зависящая лишь от логической формы понятия. Фактическое содержание – это информация, которую мы имеем в понятии с учетом значений, имеющихся в его формулировке дескриптивных терминов (знаков предметов, свойств, отношений). «С учетом значений... дескриптивных терминов» означает «с учетом некоторой совокупности знаний относительно предметов, свойств, отношений – значений этих терминов» в составе некоторой теории, в которой используется данное понятие.

Утверждение «фактическое содержание понятия хВ(х) относительно совокупности знаний Г составляет часть фактического содержания понятия хА(х) относительно той же совокупности знаний» определяется как Г, А(х) ╞ B(x).

Ясно, что если логическое содержание В – одного понятия, составляет часть логического содержания А – другого понятия, то это же отношение существует и между их фактическими содержаниями, ибо если А ╞ В, то согласно законам классической логики Г, А ╞ В для любого Г. Очевидно теперь, что фактические содержания А и Вупомянутых выше ^понятий «квадрат» и «квадрат с взаимно перпендикулярными сторонами» совпадают. Имеем Г, A ╞ В и Г, В ╞ А, где Г множество из одного высказывания – теоремы геометрии: «Во всяком квадрате диагонали взаимно перпендикулярны». Аналогичным образом устанавливаем совпадение фактических содержаний понятий «число, делящееся на 2 и на 3» и «число, делящееся на 2, на 3 и на 6», используя в качестве Г множество из 3 (истинных) утверждений арифметики: «Если некоторое число а делится на b и с, которые не имеют общего делителя, отличного от единицы, то оно делится и на их произведение», «2 и 3 не имеют общего делителя, отличного от единицы», «Шесть есть произведение двух и трех».

Логический объем понятия хА(х) составляет множество возможных предметов х, выполняющих предикат А без учета значений имеющихся в нем дескриптивных терминов, то есть рассматриваемый лишь со стороны его логической формы. Фактический объем того же понятия – это множество фактически существующих предметов, удовлетворяющих условию А с учетом значений его дескриптивных терминов.

Как уже упоминалось, объемы рассмотренных пар понятий, а также следующих – «квадрат» и «квадрат с взаимно перпендикулярными диагоналями», «число, делящееся на 2 и на 3» и «число, делящееся на 2, на 3 и на 6» равны. Теперь уточним: равны именно фактические их объемы. Что касается логических объемов, то для понятий каждой пары они различны. Именно: объем второго понятия в каждой паре уже, чем объем первого.

Действительно, если логическую форму первого понятия в первой паре, например, представить как хР(х), а второго – х(Р(х) & Q(х)), то логические объемы их соответственно представляют множество WxP(x) и Wx(P(x) & Q(х)), второе множество уже, поскольку оно равно WxP(x) ∩ WxQ(x).

Как видим из анализа последнего примера, сравнение логических объемов, как, впрочем, и фактических, можно осуществлять, подвергнув их предварительно разложению на некоторые составляющие.

Формулировка закона обратного отношения должна быть уточнена теперь с учетом проведенных различений фактических и логических содержаний и объемов понятий. Ясно, что если мы сравниваем фактические объемы (или содержания) двух понятий, то соответственно должны рассматриваться отношения между фактическими содержаниями (или объемами). Отношению между логическими объемами (или содержаниями) соответствует отношение между логическими же содержаниями (объемами). Приведенные выше примеры казались опровергающими закон обратного отношения потому, что рассматривая отношения между объемами, мы брали фактические объемы, а содержания при этом имели в виду логические!

По существу, мы имеем теперь два закона обратного отношения: с одной стороны, для фактических содержаний и объемов, с другой – для логических. Приведенная выше формулировка относится именно к этому последнему закону. В качестве обобщающей их формулировки может быть принята следующая (закон обратного отношения):

 

 

где Г указывает на то, что сравнение объемов и содержаний осуществляется с учетом совокупности знаний Г.  есть то же, что и «Г, А(х) ╞ В(х)». Однако допускается, что Г может быть пустым множеством (при непустом Г имеем фактические относительно этого Г объемы и содержания, при пустом – логические).

Этот закон играет важную роль во многих процессах познания. По существу, он является основой семантической теории информации. Само понятие семантической информации, например, информации того или иного высказывания А, определяют обычно как меру или показатель того, насколько принятие этого высказывания за истину ограничивает некоторое множество исходных возможностей М. Информативность А тем больше, чем сильнее это ограничение. Если мы, например, говорим, что данное вещество химически сложно, то ограничиваем множество химических веществ до химически сложных; утверждение же о том, что это вещество является химически сложным и состоит из кислорода и водорода, делает круг возможностей, к которому относится рассматриваемое вещество, еще более узким и, значит, является более информативным.

Наше утверждение относится, вообще говоря, не к действительности в целом, например, не к миру вообще, а к некоторым его состояниям в те или иные моменты или промежутки времени, или, как говорят в логике, к возможным мирам, которые представляют так называемые «описания состояний». На этом основан широко применяемый в логике и теории информации способ оценки информативности логических форм высказываний.

Информация при этом определяется относительно множества «возможных миров М». Логическая форма А некоторого высказывания А₀ тем более информативна, чем уже множество М_А – «возможных миров», в которых истинно Л. В понятии множество исходных возможностей – это его род. Объем понятия – результат его ограничения за счет добавления видового отличия. Степень этого ограничения и есть показатель информативности предиката, выражающего это видовое отличие.

Закон обратного отношения играет важную роль в известных операциях обобщения и ограничения понятий и в анализе отношений между понятиями.

 

Упражнения

 

1. В каком отношении находятся содержания (фактические и логические) следующих пар понятий и каково отношение между их объемами:

а) плоский замкнутый четырехугольник с равными противоположными сторонами (параллелограмм) и плоский замкнутый четырехугольник с равными сторонами (ромб) ?

б) число, делящееся на 6, и число, делящееся на 6 и на 3?

2. Известно, что всякая фигура, у которой противоположные стороны параллельны, есть фигура, у которой противоположные стороны равны. Что можно заключить из данной характеристики отношений между фактическими объемами понятий об отношении их содержаний?

Виды понятий

Вопрос о видах понятий – это прежде всего вопрос о различных способах мысленного выделения и обобщения предметов в процессе познания. Знание видов понятий важно прежде всего с гносеологической точки зрения, для понимания процесса познания. Но оно имеет и немалую практическую значимость. А именно, оно важно для понимания смыслов тех или иных утверждений, а также для обеспечения точности выражения мыслей. Таким образов, это знание является существенным моментом логической культуры мышления.

Различение видов понятий осуществляется с разных точек зрения главным образом по трем основаниям:

1) по некоторым характеристикам объемов понятий;

2) по характеру признаков, составляющих видовое отличие мыслимых предметов в понятии, точнее говоря, по характеру предиката, выражающего это видовое отличие, то есть предиката А(х) в понятии хА(х);

3) по характеру предметов, обобщаемых в понятии.

I. Среди всех возможных понятий обычно особо выделяют пустые и непустые, а среди непустых – единичные и общие. Пустые понятия имеют в качестве объема пустой класс. Полезно различать понятия логически и фактически пустые. Понятие хА(х) является логически пустым, если А(х) есть логически противоречивая характеристика предметов х. Ясно, что в силу законов логики пустым является любое понятие вида  например, «вещество, которое является кристаллическим и не является таковым». Понятие хА(х) фактически пусто, если фактически не существует предметов х с данной характеристикой А(х). Таково, например, понятие «ворон белого цвета». Не существует также, как известно, атомов в том смысле, как их понимали в Древней Греции, а именно как неделимых частиц. Однако особый и наиболее значимый случай фактической пустоты понятия таков, когда существование предметов х с характеристикой А(х) невозможно в силу законов той области действительности, к которой относится это понятие. Так, невозможны ромбы, в которых диагонали не являются взаимно перпендикулярными, невозможны неупругие жидкости, металлы, не обладающие хорошей электропроводимостью, и невозможны вечные двигатели (двигатели, работающие без дополнительной затраты энергии).

Возможность появления пустых понятий объясняется тем, что в научном мышлении понятия возникают не только о тех предметах, которые имеются налицо. На основе познанных процессов, законов часто возникают предположения о существовании или возможности появления тех или иных явлений с заранее определенными признаками («антиатомы», «жизнь на кремниевой основе» – вместо известной нам имеющей углеродную основу – и т.п.). Здесь новые понятия возникают на основе других понятий и знаний как проявления активного и творческого характера мышления. Естественно, что в таких случаях могут возникать понятия, которым, как оказывается затем, ничего не соответствует в действительности. Но в некоторых случаях наука сознательно использует пустые понятия, хотя бы для формулировок об утверждении о несуществовании соответствующих предметов и явлений и даже иногда для формулировки некоторых законов. Читателю известны, вероятно, два закона термодинамики: один из них гласит, что невозможны «вечные двигатели» 1-го рода, второй гласит то же самое о «вечных двигателях» 2-го рода.

Единичным является понятие, объем которого есть единичный класс, а общие понятия имеют в качестве объема класс, состоящий более чем из одного предмета.

Единичное понятие по сути своей представляет собой, как и всякое другое, некое обобщение и этим отличается от имени отдельного предмета. Мы не всегда при этом можем даже знать, что класс обобщаемых предметов является именно единичным. Без дополнительных знаний не ясно, например, является ли общим или единичным понятие «город, породненный с Волгоградом». Возможно, не каждому известно, что в объем этого понятия входят 9 городов в разных странах мира.

В некоторых случаях возникают трудности при попытке решить вопрос, является ли некоторое понятие общим или единичным в силу характера мыслимых в понятии предметов. Едва ли могут возникнуть сомнения насчет того, являются ли общими такие, например, понятия, как «человек», «растение», «город», «страна». Но уже не так легко определить, к какому классу относятся понятия «вода», «водород» и т.п., вообще понятия, в которых обобщаются газообразные, жидкие или сыпучие вещества, то есть объекты, трудно поддающиеся индивидуализации. Аналогичные трудности возникают с понятиями «любовь», «бытие» и т.п. (так называемые абстрактные понятия).

Полезно использовать в таких случаях следующий критерий: понятие является общим, если в пределах его объема могут быть выделены некоторые виды предметов. Так, в объеме понятия «вода» мы можем выделить: «морская вода», «речная вода», «дистиллированная» и «недистиллированная вода»- В объеме понятия «бытие» (имея в виду способ существования чего-либо), выделяют «бытие отдельного человека», «общественное бытие». (Сравним утверждения диалектического материализма «бытие определяет сознание» и «общественное бытие» определяет «общественное сознание».) «Любовь», как известно, также различают – «страстная» и «спокойная», «вечная» и «непостоянная», «бескорыстная» и «по расчету».

Еще более просто решить указанный вопрос, когда возможна индивидуализация мыслимых в понятии объектов. Так, пользуясь понятиями «талант» или «белизна», мы выделяем индивидуальные случаи: «талант Пушкина», «талант Толстого», «белизна снега», «белизна мела». Что касается понятий «вода», «водород», то элементами объема здесь являются отдельные случаи, когда мы встречаем эти вещества в природе (отдельные порции или отдельные скопления их).

Однако в данном случае речь идет о повседневном употреблении соответствующих терминов. Иное дело, когда эти термины употребляются специальным образом, например, в химии. Термин «вода» в этом случае выражает единичное понятие «химически сложное вещество, молекулы которого состоят из двух атомов водорода и одного атома кислорода». Аналогично этому «водород» есть определенное химически простое вещество или химический элемент (в связи с тем, что эти понятия являются единичными, выражающие их термины могут употребляться и как имена соответствующих веществ или элементов).

Среди общих понятий особое место занимают так называемые универсальные понятия. Универсальными являются понятия вида хА(х) объем которых совпадает с областью значений х, то есть с родом этого понятия. Это совпадение обусловлено тем, что предикат А(х) не содержит никакой информации относительно предметов рода и, значит, ничего не выделяет в этом роде. Аналогично тому, как мы среди пустых понятий различаем логически и фактически пустые понятия, мы различаем логически и фактически универсальные понятия. Например, логически универсальным является  и вообще хА(х), где А(х) есть логический закон (общезначимая формула логики предикатов).

Понятие фактически универсально, если предикат, составляющий его видовое отличие, не выражает никакой информации относительно предметов рода данного понятия и при этом именно в силу значений составляющих его дескриптивных терминов. Обычно это подразумевает наличие закона науки, указывающего на то, что все предметы рода обладают этим признаком. Так, например, фактически универсально понятие: «Жидкость такова, что давление на какую-нибудь ее точку передается во все стороны с одинаковой силой». Здесь мы имеем случай, когда содержанием понятия является закон-признак, необходимо присущий всем жидкостям (согласно закону Паскаля). Естественно, что он ничего не выделяет в множестве жидкостей, то есть не несет никакой информации относительно них, поскольку верен для любых жидкостей. Но если бы в качестве родового было взято понятие «физическое тело», тогда понятие с тем же видовым отличием выделяло бы именно жидкости.

Указанное различие внутри универсальных и пустых понятий связано с приведенным выше различением логических и фактических содержаний и соответственно объемов понятий.

Нетрудно усмотреть следующую связь между пустыми и универсальными понятиями: если хА(х) пусто, то  универсально, и наоборот, если хА(х)универсально, то  пусто.

II. По характеру признаков выделяют обычно положительные и отрицательные, относительные и безотносительные понятия.

Понятие хА(х) положительно, если А(х) выражает наличие у предметов х какого-либо свойства или отношения и отрицательно, если признак А(х) указывает на отсутствие какого-либо свойства или отношения. Пользуясь данными выше определениями положительного и отрицательного признаков, можно сказать, что понятие является положительным или отрицательным в зависимости от того, положительным или отрицательным является признак А(х).

Понятие хА(х) положительно, если А(х) выражает наличие у предметов х каких-то свойств или отношений. Положительными являются, например, понятия «европейское государство», «столичный город», «родственники». Примеры отрицательных понятий – «человек, не знающий логики», «непересекающиеся прямые», «нечестный и безнравственный человек».

Безотносительным или относительным понятие является в зависимости от того, представляет ли его видовое отличие атрибутивное или реляционное свойство (см. § 13). Безотносительными являются, например, понятия; «кристаллическое вещество», «преступное действие», «общественный прогресс». Относительными будут: «отец Сократа», «столица Франции», «столица какого-нибудь государства». Можно выделить три основных вида относительных понятий по их знаковым формам:

 

 

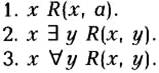
Первые два из только что приведенных примеров относительных понятий относятся к виду 1. Третий – к виду 2. Понятиями, относящимися к виду 3, будут «студент, сдавший все экзамены сессии», «человек, не знающий ни одного иностранного языка».

III. По характеру обобщаемых в понятии объектов следует различать прежде всего понятия, в которых обобщаются отдельные предметы того или иного типа (видаХА(Х)) и системы объектов (понятия вида (Х₁, ..., Х_k) A(Х₁, ..., Х_k), k > 1). Примеры первых: «живое существо», «плодовое дерево», «город, находящийся на Экваторе» и т.п. К числу вторых относятся: «параллельные прямые», «изотопы», «родственники», «супруги», «однокоренные слова», «друзья».

Дальнейшее подразделение относится к понятиям вида ХА(Х), то есть к понятиям, в которых обобщаются отдельные предметы. При этом различаются понятия конкретные и абстрактные, с одной стороны, собирательные и несобирательные – с другой. Первое из указанных делений связано с Различением конкретных и абстрактных объектов (см. § 12).

Напомним, что конкретными объектами мы называем вещи, ситуации и процессы реальный действительности, а также результаты той или иной идеализации таких предметов (абсолютно упругие жидкости, абсолютно черные тела) и, наконец, множества и системы предметов указанных типов, мыслимые как целое.

Абстрактные объекты – суть создания мысли, идеальные предметы. Каковы те или иные характеристики конкретных предметов (свойства их, предметно-функциональные характеристики или отношения между ними), отвлеченные от соответствующих предметов и ставшие самостоятельными объектами мысли. Так возникают «числа», «фигуры», «движение». К множеству объектов этого типа можно, очевидно, также отнести параллели, меридианы, векторы и т.п.

Конкретным, является понятие, элементы объема которого – конкретные объекты. Таковы понятия, составляющие смысл выражений «человек», «социалистическая революция», «растение», «государственная собственность некоторой страны» и т.п. Абстрактные понятия в качестве элементов объема имеют абстрактные объекты. Таковы понятия: «число», «геометрическая фигура», «арифметическая функция», «рефлексивное и симметричное (двухместное) отношение», а также «производительность труда», «прибыль, получаемая предприятием» и т.п.

Заметим, что в логической литературе определения конкретных и абстрактных понятий не вполне совпадают с данными здесь их характеристиками. Обычно говорят, что элементами конкретных понятий являются предметы, представляющие собой – с логической точки зрения – некоторые системы признаков, то есть некоторые конкретные предметы, а элементами объема абстрактных понятий являются отдельные характеристики (стороны, свойства) конкретных предметов. Понятие «геометрическая фигура» относится в таком случае к числу конкретных понятий, а абстрактными будут: «площадь геометрической фигуры», «замкнутость геометрической фигуры» и т.п.

Однако это различение весьма неопределенно, поскольку и отдельные свойства, и отношения предметов в свою очередь представляют собой какую-то систему свойств (более высокого порядка) и поэтому подходят под определение конкретных объектов. Впрочем, и та граница, которая подразумевается в различении, проведенном нами первоначально, тоже не является вполне четкой. Как известно, нет строгих граней даже между более простыми предметами и явлениями действительности, и почти любое различение видов тех или иных предметов в той или иной степени условно и неопределенно.

Понятие свойства (как и отношения) возникает в результате двойного абстрагирования. С одной стороны, происходит отвлечение некоторого свойства от предметов – изоляция его от предметов и превращение в самостоятельный предмет (изолирующее абстрагирование); с другой стороны, осуществляется обобщение этого свойства путем выделения общих основных свойств этих свойств и отвлечения от остальных (обобщающе-различающее абстрагирование).

Существуют неясности, связанные с абстрактными понятиями. Например, бывают они общими или только единичными, как считают многие авторы учебников по логике? Имеет ли смысл их деление на относительные и безотносительные?

Ясно, что среди абстрактных понятий имеются как общие, так и единичные. Независимость государства имеет виды: политическая независимость, экономическая независимость и т.д. Это означает, что понятие является общим. Далее, если иметь в виду абстрактные понятия, в которых мыслятся свойства, отношения и тому подобные характеристики конкретных предметов, то все они, очевидно, являются относительными, поскольку для содержания каждого такого понятия обязательными являются указания на принадлежность мыслимой характеристики тому или иному отдельному предмету или каким-то из предметов некоторого класса. Например, «независимость Украины», «независимость (некоторого, какого-либо) государства».

Значительная доля условности имеется и в делении понятий на собирательные и несобирательные. Несобирательными называются понятия, предметы которых представляют собой нечто целое, хотя и состоящее возможно из каких-то различных частей, но мыслимое как нерасчлененное целое. Например, «физическое тело», «человек», «растение». Конечно, каждое тело является, как мы знаем, совокупностью молекул и других частиц, но в несобирательном понятии мы отвлекаемся от его структуры и вообще от того, что оно представляет собой какую-то структуру. Предметы, обобщаемые в собирательных понятиях, то есть элементы объема такого понятия, это некоторая совокупность (возможно, даже отдельно существующих предмете) или система предметов, мыслимая как целое. Например, «производственная бригада», «народ», «флот», «лес» и т.п. Объем понятия «производственная бригада» есть совокупность всех возможных производственных бригад (таким образом, понятие является общим), и содержание понятия «совокупность людей, соответствующим образом организованных для выполнения определенных производственных задач» относится к каждой из них, но, конечно, не к отдельным членам бригады. Очевидно, что собирательное понятие может быть и единичным, например, «студенческий коллектив МГУ», «созвездие Большой Медведицы» и др.

Отдельные предметы, составляющие совокупности, мыслимые в собирательном понятии, вообще говоря, существуют или могут существовать отдельно или самостоятельно. Но в некоторых отношениях их совокупность выступает как одно целое (например, перед всеми людьми, составляющими производственный коллектив, стоят некоторые общие задачи, и все они в совокупности несут ответственность за их выполнение и т.д.). Это обусловливает возможность и необходимость в некоторых случаях мыслить совокупность как один предмет. Иногда говорят, что собирательные понятия могут употребляться в разделительном смысле. Так, как будто, употребляется собирательное понятие «данный коллектив» в суждении: «Все члены данного коллектива справились со своим заданием».

Однако точнее сказать, что в данном суждении сам предмет (данный коллектив), а не понятие, берется разделительно, хотя бы потому, что члены коллектива являются частями коллектива, но не являются ни частями, ни элементами объема понятия «данный коллектив». Понятие «данный коллектив» – в своем обычном собирательном смысле – мы используем здесь для образования нового (общего) понятия «член данного коллектива». Это – общее, несобирательное, относительное понятие, в котором мыслится отношение людей к определенному предмету, именно к данному коллективу.

Другой вид также общего и относительного понятия, представляющий собой обобщение только что рассмотренного, представляет понятие «член коллектива» (член какого-нибудь коллектива).

К числу приведенных – обычно рассматриваемых делений в учебной литературе – полезно добавить деление понятий на эмпирические и теоретические. В эмпирических понятиях основное содержание составляют признаки, доступные наблюдению, например, «жидкость, не имеющая цвета, запаха и вкуса» (вода – в обыденном смысле). В теоретических понятиях наличие этих признаков у предметов устанавливается посредством некоторого теоретического анализа. Например, «химически сложное вещество, молекулы которого состоят из двух атомов водорода и одного атома кислорода» (вода – как особое химическое вещество). Еще примеры эмпирических и теоретических понятий: температура как «степень нагретости тела» в смысле ощущения его как более теплого или менее теплого (эмпирическое понятие), «величина, характеризующая физическое тело, значение которой определяется посредством термометра» (эмпирическое понятие); «характеристика физического тела, значение которой равно средней кинетической энергии движения молекул» (теоретическое понятие).

Мы видели, что грани между некоторыми выделяемыми видами понятий не всегда являются достаточно четкими. Однако это не умаляет ценности этих делении (тем более, как уже подчеркивалось, во многих классификациях даже более простых объектов есть моменты условности, неопределенности, огрубления и т.д.). К тому же деление понятий на виды имеет не столько практическое, сколько теоретическое значение. Оно важно с гносеологической точки зрения, поскольку различные виды понятий представляют собой в то же время различные способы мыслительной деятельности.

В многообразии видов понятий выражается активный и сложный характер отражения мира в мышлении, соответствующий сложности и многосторонности познаваемой нами действительности. Предметами понятий, как мы видели, могут быть отдельные предметы и их характеристики (свойства, отношения и т.д.). Предметы – и даже одни и те же – могут обобщаться по различным их сторонам, по наличию и отсутствию свойств, качеств, отношений, по собственным характеристикам предмета и по отношению его к другим предметам и т.д.

Совокупности взаимосвязанных предметов могут мыслиться разрозненно и, наоборот, возможно мысленное объединение в некоторый агрегат предметов, существующих раздельно, и т.д., и т.п. Знание этих способов позволяет овладеть, понятием как одной из форм мышления. Это важно также и для того, чтобы умело пользоваться имеющимися в нашем распоряжении понятиями в процессе рассуждения.

 

Упражнения

 

Дайте характеристики следующих понятий (укажите, к каким видам они относятся):

а) хвойное дерево;

б) плодовое растение;

в) промышленное предприятие;

г) самое большое число;

д) промышленное предприятие, не имеющее связей с другими предприятиями;

е) социал-демократическая партия;

ж) член (какой-нибудь) социал-демократической партии;

з) породненные города;

и) член труппы какого-нибудь театра;

к) население государства, расположенного на Северном полюсе;

л) численность населения государства, расположенного на Южном полюсе;

м) равнодействующая всех сил, действующих на Землю.

 

Виды отношений между понятиями

Для того, чтобы правильно оперировать понятиями – в этом состоит одна из целей изучения теории понятия – необходимо учитывать, что они существуют в системе знания не изолированно, а находятся в каких-то отношениях между собой. Эти отношения многообразны. Можно выделить, по крайней мере, два типа таких отношений. Один тип – отношения теоретико-множественной (экстенсиональной) природы. Это отношения между классами, которые представляют объемы понятий, хотя и зависят определенным образом от содержаний понятий. Другого типа отношения возникают в процессе познания, когда возникают вопросы: может ли быть познано одно явление, если не познано другое? знание каких явлений необходимо для познания других? и соответственно о том, какие понятия необходимы, и даже в какой степени, для определения других? и что необходимо для определения первых?

Примером такой субординации понятий может служить определение истинных солнечных суток: «Истинные солнечные сутки – это промежуток времени между двумя непосредственно следующими друг за другом истинными полуднями. Истинный полдень (в данном месте) – это момент верхней кульминации центра солнечного диска (светила вообще). Кульминация центра солнечного диска – это явление прохождения центра диска Солнца через небесный меридиан, а верхняя кульминация – это прохождение центра диска через меридиан верхней части небесной сферы. Небесный меридиан – это линия, в которой плоскость небесного меридиана пересекает небесную сферу. Плоскость небесного меридиана – это плоскость, проходящая через точку зенита центра небесной сферы и полюс мира. Точка зенита – это наивысшая точка небесной сферы над головой наблюдателя. Полюсы мира – это точки пересечения оси мира с небесной сферой. Ось мира – это ось суточного вращения небесной сферы. Центр небесной сферы – это глаз наблюдателя. Небесная сфера – это воображаемая шаровая поверхность, на которую мы проецируем положение небесных тел. Верхняя часть небесной сферы – это часть небесной сферы, лежащая на плоскости небесного экватора. Плоскость небесного экватора – это плоскость, перпендикулярная оси мира и проходящая через центр небесной сферы».

Однако в логике пока нет теории, описывающей отношения этого (последнего) типа. Но довольно детально разработана теория отношений первого типа. Мы ограничимся рассмотрением только этих отношений.

Здесь имеются в виду отношения между парами понятий по их содержаниям и по их объемам. Те и другие отношения, как мы увидим далее, определенным образом связаны между собой. Выяснение отношений между содержаниями может быть связано с вопросами: является ли содержание одного понятия более широким, чем содержание другого, или, могут ли признаки, составляющие содержание одного и другого, принадлежать одним и тем же предметам? Об объемах двух понятий соответственно можно спросить: является ли объем одного понятия уже объема другого, или, имеются ли такие предметы, которые одновременно являются элементами объема и одного, и другого понятия?

Обратим внимание сразу на то, что надо отличать отношения понятий о тех или иных предметах от отношений между самими предметами, тем более что имеются даже общие термины для обозначения отношений того и другого типа. Так, мы говорим, что крыло самолета является частью самолета, а объем понятия «реактивный самолет» является частью объема понятия «самолет». Городской район – часть города, но объем понятия «городской район», конечно, не является частью объема понятия «город». Отношения «часть» – «целое» между предметами называются мернологическими; рассматриваемые здесь отношения между понятиями – это логические отношения (при этом определенного типа, связанные именно с указанными выше вопросами. Возможны и другие отношения: например, в системе понятий той или иной науки одни понятия определимы через другие, но не наоборот и т.д.).

Однако и среди интересующих нас отношений между понятиями возможно различение отношений по логическим и фактическим содержаниям и соответственно объемам. В дальнейшем речь будет идти об отношениях между фактическими содержаниями (и объемами) относительно всех вообще имеющихся на данный момент знаний в повседневном обиходе или в соответствующей науке, к которой относится понятие.

Кроме того, надо заметить, что в практике научного познания возникают ситуации, когда надо определить отношения между множеством понятий, состоящим из более чем двух понятий. Но задача в этом случае сводится к более простой: к выяснению отношений данного множества понятий попарно.

I. Любые два понятия прежде всего являются сравнимыми или несравнимыми. Два понятия сравнимы, если они имеют общий род. В противном случае понятия несравнимы. Например, понятия «плоская геометрическая фигура (род), замкнутая и ограниченная четырьмя прямыми (видовое отличие)» и «плоская геометрическая фигура (род), замкнутая и ограниченная тремя прямыми (видовое отличие)» являются сравнимыми. Но «плоская, замкнутая геометрическая фигура (род), ограниченная четырьмя сторонами», не является сравнимым понятием ни с одним из указанных. Обратим внимание на то, что обычно сравнимыми называют понятия, предметы которых имеют какие-то общие признаки, если же у предметов, мыслимых в понятии, нет никаких общих признаков, то они несравнимы. Однако, строго говоря, все предметы, поскольку понятие «предмет» употребляется здесь в широком смысле «как предмет мысли», имеют какие-то общие признаки, хотя бы именно тот, что они являются или могут быть предметами мысли. Кажутся явно несравнимыми, например, понятия «радость» и «искусственный спутник Земли». Однако, если мы их сформулируем так, что возьмем в качестве рода множество никак не охарактеризованных предметов («нечто») и все остальные характеристики, по которым выделяем соответствующие объекты мысли, отнесем к видовым отличиям, то понятия оказываются сравнимыми. Таким образом, существенно обращать внимание на строение (формулировку) понятия.

При указанном выше способе сравнения содержаний понятий по информативности на основе отношения логического следования предполагается, что понятия имеют общий род, а сравниваются части содержаний, заключенные в видовых отличиях. Приведение подлежащих сравнению понятий к общему роду так же необходимо, как приведение сравниваемых дробей к общему знаменателю, и только при осуществлении такого приведения они становятся сравнимыми. Из данных разъяснений напрашивается мысль, что все понятия сравнимы, поскольку они могут быть всегда приведены к общему роду. Однако в определении сравнимости мы имеем в виду не возможность, а фактическое положение дел. И это существенно, поскольку понятие, полученное из какого-либо понятия изменением его рода, представляет собой уже иное понятие, чем исходное.

II. Среди несравнимых понятий не существует уже никаких отношений. В множестве пар сравнимых понятий выделяются совместимые и несовместимые. Понятия совместимы, если признаки, составляющие содержание этих понятий, могут принадлежать одним и тем же предметам, их объемы имеют какие-то общие элементы. В противном случае понятия несовместимы. Например, совместимыми являются понятия: «активист» и «отличник», «философ-материалист» и «философ-метафизик», «философ-идеалист» и «философ-диалектик» и т.п. Здесь, как и в дальнейших примерах, подразумевается, что понятия сформулированы так, что они имеют общий род. Для первой пары понятий общим родом может быть класс людей или класс учащихся, для остальных – класс людей.

Необходимым и достаточным условием логической несовместимости понятий хА(х) и хВ(х) является пустота пересечения их объемов: WxA(x) ∩ WxB(x) = O. Для содержаний понятий в этом случае имеем  При этом, в случае логической несовместимости понятий, Г пусто (значит, может быть любым). При фактической несовместимости Г – некоторое непустое множество высказываний, относящихся к дескриптивным терминам в А(х) и В(х) (и любое его расширение).

В силу того, что Г есть множество высказываний (замкнутых формул), логическая несовместимость указанных понятий означает логическую истинность выражений  (логическая истинность формул означает истинность лишь в силу логических форм, независимых от значений дескриптивных терминов в них).

При фактической несовместимости эти выражения истинны в силу значений, имеющихся в А(х) и В(х) дескриптивных терминов.

Для совместимых понятий имеем: WxA(x) ∩ WxB(x) = O и истинное высказывание  При этом для логической совместимости это высказывание истинно лишь в силу своей логической формы (то есть истинно независимо от значений дескриптивных терминов в составе форм А(х) и В(х)). Фактическая совместимость означает истинность указанных высказываний в силу данных значений дескриптивных терминов в А(х) и В(х) и, значит, с учетом некоторого множества знаний Г относительно этих терминов.

Несовместимые понятия: «студент – отличник» и «неуспевающий студент», «интернационалист» и «националист», «кристаллическое вещество» и «вещество, не имеющее определенной температуры плавления».

Ясно, что для решения вопроса о совместимости или несовместимости понятий нужно иметь сами понятия, а не слова, которые служат их сокращениями. Так, если молекулой называется наименьшая частица вещества, обладающая его химическими свойствами, то совместимыми, очевидно, являются понятия «молекула» и «атом», поскольку имеются так называемые одноатомные молекулы (например, молекулы инертных (благородных) газов).

Кстати, автор статьи «Молекула» в БСЭ (изд. 3-е), сформулировав указанное в начале определение ее, вместе с тем замечает, что «одноатомные молекулы по сути дела являются атомами вещества и поэтому (? – Д., В.), строго говоря, не могут быть отнесены к молекулам». Автор здесь противоречит сам себе. Согласно его определению молекулы, одноатомная молекула является молекулой в строгом смысле слова.

ВИДЫ СОВМЕСТИМОСТИ

В множестве пар совместимых понятий различаются три вида: 1) равнозначные понятия; 2) понятия, находящиеся в отношении логического подчинения; 3) перекрещивающиеся понятия. Равнозначными называются понятия, объемы которых совпадают и только содержания различны. Таким образом, эти понятия выделяют один и тот же класс предметов, но по разным совокупностям признаков. Например, «равносторонний треугольник» и «равноугольный треугольник» (в Эвклидовой геометрии); «тело, на которое не действуют никакие силы, или равнодействующая всех сил равна нулю» и «тело, которое находится в состоянии покоя или равномерного прямолинейного движения», «студент, для которого не существует таких вопросов (данного) курса, на которые он не может ответить» и «студент, который может ответить на все вопросы (данного) курса».

Для содержания равнозначных понятий хА(х) и хВ(х) существует их эквивалентность А(х) = В(х), что означает Г, А(х) ╞ В(х) и Г, В(х) ╞ А(х). Если эти соотношения имеются при пустом Г – понятия логически равнозначны; если же только при некотором непустом Г (и, естественно, при всех возможных расширениях его в этом случае), то они оказываются фактически равнозначными (относительно этого Г).

Понятия в приведенных выше двух первых примерах фактически равнозначны (относительно множества аксиом геометрии и относительно множества утверждений физики), а в последнем имеем логическую равнозначность понятий, что очевидно в силу логических форм этих понятий  и 

Относительно множества утверждений арифметики равнозначны «целое положительное число, отличное от 1 и не имеющее никаких делителей кроме себя и 1» и «целое положительное число, имеющее ровно два различных делителя» (в том и другом понятии выделяется класс простых чисел).

Понятия находятся в отношении логического подчинения, если объем одного из них составляет правильную часть объема другого (а содержания – в соответствии с законом обратного отношения – находятся в обратном отношении).

Понятие с более широким объемом называется подчиняющим, а другое – подчиненным. Примеры: «четырехугольник» и «прямоугольный четырехугольник», «философ» и «философ-материалист», «международные отношения» и «международные экономические отношения», «химически простое вещество» и «металл», «учащийся вуза» и «студент» («учащийся вуза или среднего специального учебного заведения»).

Для понятий хА(х) и хВ(х), находящихся в отношении логического подчинения, имеем:  и  В случае пустого Г существует родовидовое отношение логического характера, при непустом Г – родовидовое отношение фактического характера (относительно Г). Таковы отношения понятий во всех указанных примерах, кроме последнего.

Отношение логического подчинения иначе характеризуют как родовидовое, называя понятие, объем которого включает объем другого в качестве своей правильной части, родовым по отношению к этому второму, а второе – видовым по отношению к первому. Класс предметов, составляющих объем родового понятия, называют родом для класса предметов, мыслимых во втором понятии, а этот второй класс, наоборот, видом предметов данного рода.

Перекрещивающимися называют такие понятия, в объемах которых имеются общие элементы, однако в составе каждого из них содержатся такие предметы, которые не являются элементами другого. Например, «участник движения за ядерное разоружение» и «предприниматель», «поэт» и «драматург», «студент» и «спортсмен» и т.п. Для перекрещивающихся понятий хА(х) и хВ(х) верно утверждение  с учетом некоторого Г – в случае фактического перекрещивания или без учета Г – логическое отношение перекрещивания.

ВИДЫ НЕСОВМЕСТИМОСТИ

Среди несовместимых понятий выделяются пары противоречащих, противоположных и соподчиненных понятий.

Противоречащими являются понятия вида хА(х) и хВ(х), где  и где В(х) в свою очередь неэквивалентно отрицанию некоторой формулы С(х), то есть такие, в одном из которых мыслятся предметы, лишенные каких-либо свойств, составляющих видовое отличие предметов, мыслимых в другом.

Эквивалентность  может быть фактической или логической. В общем случае наличие ее означает  При пустом Г эти понятия логически противоречивы: при наличии же этих отношений только при некотором непустом Г имеем отношение фактического противоречия (относительно данного Г). Для логически противоречивых понятий хА(х) и хВ(х) логически истинны высказывания  При фактической противоречивости этих понятий данные высказывания истинны в силу значений дескриптивных терминов в составе А(х) и В(х).

Примеры противоречащих понятий: «город, являющийся столичным» и «город, не являющийся столичным», «слово, изменяющееся по числам и падежам» и «слово, не изменяющееся по числам или не изменяющееся по падежам», «тело (материальное), находящееся в покое или в состоянии равномерного прямолинейного движения» и «тело, которое не находится в покое и не находится в состоянии равномерного прямолинейного движения».

Фактически противоречащими являются понятия «равносторонний прямоугольный четырехугольник» и «четырехугольник, у которого диагонали в точке пересечения не делятся пополам», «ромб» и «неравносторонний четырехугольник».

К числу противоположных понятий относят, например, такие, как «человек высокого роста» и «человек низкого роста», «черное» и «белое», «человек высоконравственный» и «безнравственный человек». Обычно мы более или менее удачно применяем термин «противоположности» при интуитивном его употреблении. Определение же его смысла является трудной проблемой. Как правило, в этом отношении находятся понятия, которые отражают крайние степени какой-либо интенсивности. Более конкретно речь идет о понятиях, объемы которых составляют два крайних вида в множестве видов, которые выделены и расположены по степени изменения какого-нибудь признака. Так, например, объем понятия «ахроматический цвет» можно разделить по степени яркости на «белый», «светло-серый», «серый», «темно-серый», «черный». Таким образом, «белый» и «черный» здесь оказываются противоположностями. По-видимому, в любом случае, говоря о противоположных понятиях, мы подразумеваем возможность какого-либо упорядочивания видов предметов, входящих в его объем.

Среди философских систем различают материализм (исходное положение которого состоит в том, что материя первична, а сознание вторично, то есть является продуктом развития материи), дуализм (согласно представлениям которого материя и сознание существуют независимо друг от друга), идеализм (считающий, что сознание – идея, духовное вообще – первично, материя – вторична). Таким образом, идеализм есть противоположность материализма.

Наконец, два несовместимых понятия, которые не являются ни противоречащими, ни противоположными, называются соподчиненными. Например, «прямолинейное движение» и «криволинейное движение», «животное» и «растение» и т.п.

Приняты следующие графические изображения отношений между объемами совместимых и несовместимых понятий.

 

 

 

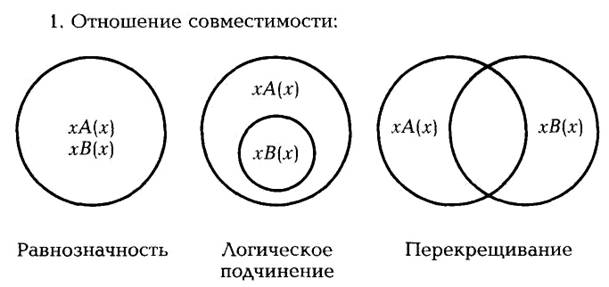
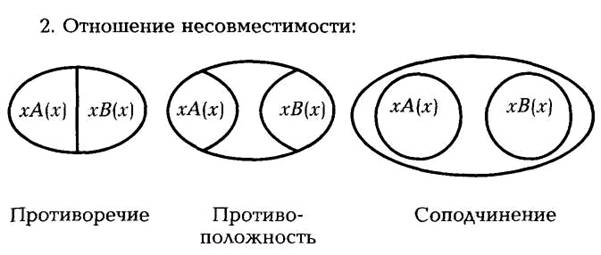
Каждой из указанных схем может быть сопоставлена совокупность некоторых высказываний. Так, схема логического подчинения указывает на истинность высказывания: «Всякий предмет из области х, обладающий характеристикой В, есть предмет, имеющий характеристику А и только некоторые предметы, имеющие характеристику А суть предметы, обладающие характеристикой В», и «Всякий предмет из области х есть А или В». Читателю предлагается самому проанализировать с указанной точки зрения все другие схемы.

Таким образом, связывая схемы с определенным высказыванием, мы имеем некоторый способ проверки того, правильно ли определено отношение между теми или иными понятиями. Например, изобразив отношение между понятиями «слово» – А и «существительное» – В схемой  мы принимаем за истинные утверждения: «всякое существительное есть слово» и «только некоторые слова суть существительные». Если же А есть «слово», а В – «корень слова», то при таком же изображении отношения между этими понятиями нужно было бы признать, что «Всякий корень слова есть слово». Но при том употреблении термина «слово», которое принято в лингвистике, это, очевидно, неверно.

Дело в том, что корень слова – это не вид слова, а его часть. Между понятиями нет родовидового отношения.

Для успешного решения вопросов об отношении тех или иных понятий, естественно, нужно точное знание содержания, а тем самым и объема понятий. Как, например, решить вопрос об отношении между понятиями «дерево, имеющее лиственную крону» и «дерево, имеющее хвойную крону», не имея понятия «листья»? Если хвоя – вид листьев, тогда второе является подчиненным первому. Однако часто знание отношений между понятиями, а тем более процесс их установления способствует уточнению, углублению содержаний употребляемых понятий. И, конечно, овладение процедурой выяснения отношений между понятиями способствует развитию аналитических способностей мышления.

 

Упражнения

 

1. Какие из следующих отношений между понятиями являются отношениями «рода и вида», а какие отношениями «часть и целое»:

а) школа, средняя школа; б) четырехугольник и сторона четырехугольника; в) натуральный ряд чисел, геометрическая прогрессия; г) ромб, квадрат; д) Китай, Азия; е) множество натуральных чисел, множество четных натуральных чисел; ж) часть Китая, часть Азии; з) кислота, химически сложное вещество?

2. Изобразите посредством круговых схем отношения между понятиями:

а) естественный спутник какого-нибудь небесного тела, спутник Земли, небесное тело, спутник Марса, спутник какого-нибудь небесного тела, искусственный спутник какого-нибудь небесного тела;

б) мужество, упорство, упрямство;

в) дед, сын, брат, мужчина, отец, внук, дядя, племянник;

г) уравнение, уравнение с целочисленным решением, уравнение, не имеющее решения, уравнение с решением в рациональных числах;

д) окружность, геометрическое место точек, равноудаленных от одной точки, полусфера, дуга окружности, сфера;

е) корень квадратный из 4, четное число, нечетное число, корень квадратный из 9, число, деление на которое дает то же число; число, на которое не делится никакое число; корень квадратный из 1;

ж) слово, изменяющееся по лицам; слово, изменяющееся по падежам, спрягаемое слово, глагол, прилагательное, наречие, существительное.

3. Укажите какие-нибудь понятия, отношения между которыми удовлетворяют следующим схемам:

 

 

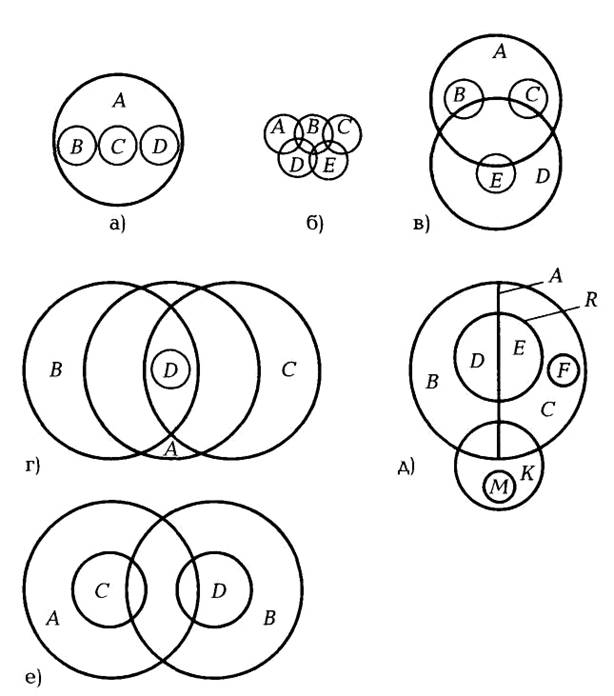
4. Какие отношения между понятиями «объективный человек», «честный человек» и «справедливый человек» имеются в виду в утверждениях (изобразите эти отношения посредством круговой схемы):

а) ни один необъективный человек не является справедливым;

б) некоторые честные люди справедливы и наоборот;

в) ни один честный не является необъективным (При затруднении обратитесь к разделу «Непосредственные выводы из категорических суждений» § 36.)?

5. Опрос 100 студентов дал следующие результаты о количестве изучающих различные иностранные языки: английский – 28, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5, все три языка – 3.

а) Сколько студентов не изучает ни одного языка?

б) Сколько студентов изучает только французский язык?

в) Сколько студентов изучает только немецкий язык?

г) Сколько студентов изучает только английский язык?

д) Сколько студентов изучает немецкий язык в том и только в том случае, если они изучают французский язык?

е) Сколько студентов изучает немецкий язык в том и только в том случае, если они не изучают английский язык?

(Указание. Нарисуйте схему в виде трех кругов, обозначающих студентов, изучающих соответственно английский, французский и немецкий языки. В каждую из полученных областей впишите цифры, исходя из условия задачи.)

ОПЕРАЦИИ С ПОНЯТИЯМИ

Выше мы познакомились со структурами понятий, с их видами и видами отношений между ними. Но главная цель теории понятия состоит в том, чтобы овладеть понятиями как некими средствами познания, выработать практические навыки правильного оперирования ими. Приступая к изучению операций с понятиями, мы подходим как раз к выяснению таких аспектов, которые позволяют приобрести эти навыки.

Здесь мы имеем в виду некоторые основные операции с понятиями, к числу которых относятся обобщение и ограничение понятий и деление понятий. Частным видом деления является классификация. Обычно к числу операций с понятиями относят также и определение. Но это связано с неправильной трактовкой этой операции как операции, посредством которой раскрывается содержание понятия. Посредством определения понятия обычно вводятся в науку, хотя это не единственная функция данного приема познания.

§ 22. Обобщение и ограничение понятий

Обобщение некоторого понятия есть операция образования из этого понятия некоторого нового с более широким объемом, что означает обобщение и выделение более широкого круга предметов. Обратная операция перехода от некоторого понятия к понятию с меньшим объемом называется ограничением понятия. В математике, например, особенно в геометрии, обычно мы идем от наиболее общих понятий к менее общим: от характеристики треугольников вообще к характеристикам отдельных видов треугольников – прямоугольных, равносторонних, равнобедренных и т.д. От четырехугольников – к ромбам, квадратам. Хотя в той же математике имеют место и обратные процессы. Например, от рассмотрения целых положительных и целых отрицательных чисел – к целым числам вообще, от целых и дробных – к рациональным и иррациональным, затем – к действительным. В опытных науках, таких, например, как биология, учащиеся начинают изучение с некоторых видов знакомых (наблюдаемых) растений и животных и идут затем к обобщениям введенных понятий и рассмотрению, таким образом, более широких классов организмов.

В изучении материала движение тем или иным образом зависит в значительной мере от степени сложности самих понятий, от степени трудности выделения видообразующих, в совокупности отличительных признаков того или иного класса предметов.

Переход от данного понятия к понятию с более широким объемом – обобщение понятия – осуществляется за счет определенного ослабления содержания первого. Так, от понятия «повествовательное предложение» переходим к понятию «предложение», исключая из содержания этого понятия указание на то, что в грамматической форме этого типа о чем-то сообщается. От понятия «серная кислота» как вида кислоты переходят к понятию «кислота», от последнего как вида химически сложного вещества,– к понятию «химически сложное вещество» и далее – к понятию «вещество» вообще.

Ясно, что обратная операция перехода от некоторого понятия к понятию с меньшим объемом – ограничение понятия – осуществляется за счет расширения содержания исходного. Ограничивая понятие «вещество», получаем понятие «химически сложное вещество», затем «кислота», «серная кислота».

В этих примерах мы имеем, очевидно, уже не отдельные акты обобщений и ограничений, а и последовательности таковых, соответствующие определенным процессам мышления – так называемого восхождения от отдельного или особенного к общему, от него – к более общему и т.д. и, наоборот,– процесс движения от общего к конкретному (особенному или отдельному). В процессах такого рода необходима определенная последовательность. Другими словами, надо избегать скачков в обобщениях и ограничениях. Это значит, что каждый акт обобщения должен быть переходим от вида к некоторому ближайшему роду. При ограничении – наоборот: от рода к некоторому ближайшему виду. Зная, например, что-то о серной кислоте, мы можем ставить вопрос: нельзя ли это высказать о кислоте вообще или даже о всех химически сложных веществах? Но переходя сразу, например, от серной кислоты к химически сложному веществу, мы затруднили бы процесс проверки правомерности обобщения наших знаний. Конечно, проверку такого рода легче осуществлять последовательно, «шаг за шагом».

Кроме того, мы видим, что ограничение одного и того же понятия может идти по разным направлениям. Аналогично имеются различные возможности обобщения одного и того же понятия. От понятия «равносторонний прямоугольный четырехугольник» можно перейти как к понятию «равносторонний четырехугольник», так и к понятию «прямоугольный четырехугольник». Ограничение понятия есть его конкретизация, которая связана с учетом особенностей при образовании более узкого понятия. Обобщение, наоборот, связано с приемом абстрагирования, отвлечения от каких-то особенностей, мыслимых в понятии предметов. Короче говоря, ограничение есть выделение особенного в пределах чего-то общего, а обобщение – переход от особенного к чему-то общему.

Наряду с данными определениями операций обобщения и ограничения эти операции имеют и другие важные характеристики. Так, полезно еще раз заметить, что обобщение – это переход от данного понятия к некоторому его роду, а ограничение, наоборот,– от рода (данного понятия) к некоторому его виду. В терминах, описанных выше отношений между понятиями, обобщение представляет собой переход от подчиненного понятия к подчиняющему, а ограничение – наоборот. С точки зрения объемов понятий, то есть с экстенсиональной точки зрения, это – переходы от подмножеств (подклассов) к множествам (классам) и наоборот.

Отношение вида и рода, как мы уже раньше подчеркивали, надо отличать от отношения «часть и целое» между предметами. Аналогично, не следует смешивать обобщение понятий (например, переход от понятия «прямоугольный треугольник» к понятию «треугольник») с переходами – в процессе мысленного оперирования с предметами – от части к целому (например, переход от «стороны треугольника» к «треугольнику»). В первом случае мы можем сказать: «Всякий прямоугольный треугольник есть треугольник». Но сторона треугольника, конечно, не является треугольником!

Потребность в обобщении понятий возникает, в частности, при необходимости обобщения формулировок законов науки. Как мы знаем, в обычной формулировке закона Архимеда он представляет собой утверждение, относящееся к классам жидкостей и твердых тел. Однако закон справедлив и для газообразных тел (и обычно применяется в аэродинамике). Для его обобщения должно быть обобщено понятие жидкости так, чтобы обобщенное понятие охватывало и жидкости, и газы. Таковым является, например: «Вещество, в массе которого давление на любую его часть передается во все стороны с одинаковой силой».

Но нередко в познании возникает необходимость также ограничения закона науки, распространения закона, относящегося к классу предметов, мыслящихся в понятиихА(х) на некоторый частный случай (вид предметов) хВ(х).

Нетрудно видеть, что операции обобщения и ограничения понятий связаны с законом обратного отношения. Если понятие хА(х) является обобщением понятия хВ(х), а второе, очевидно, в этом случае – результат ограничения первого, то для объемов этих понятий имеем  (объем второго составляет правильную часть первого или является собственным подмножеством первого, причем, вообще мы можем иметь здесь в виду либо фактические, либо логические объемы понятий). Содержание первого понятия является частью содержания второго, то есть Г, В(х) ╞ A(x), но не наоборот  (Можно сказать, что содержание первого составляет правильную часть второго.)

При непустом Г имеем отношение между фактическими содержаниями, при пустом – между логическими. В зависимости от того, имеем ли указанное отношение между логическими объемами и содержаниями понятий или фактическими, различаем также фактические и логические обобщения и ограничения понятий.

Наиболее распространенными в практике являются обобщения логического характера, однако учитывать указанное различие существенно хотя бы для того, чтобы отличать фиктивные обобщения либо ограничения от действительных. В практике научного познания обычно представляют интерес фактические обобщения и, как правило, они в то же время являются и логическими (таковы обобщения во всех приведенных выше примерах). Но, например, ограничение понятия «равносторонний четырехугольник» до понятия «равносторонний четырехугольник со взаимно перпендикулярными диагоналями» является логическим, но не представляет собой фактического ограничения. По существу, логические обобщения и ограничения, которые не являются в то же время фактическими, представляют собой фиктивные обобщения и ограничения, хотя не исключено, что в каких-то процессах познания могут представлять интерес и чисто логические операции указанных типов.

В свете сказанного выявляется явная неточность определения самих операций обобщения и ограничения понятий в традиционной логике. Обобщение здесь определялось как переход от некоторого понятия к другому, более широкому по объему за счет исключения из содержания исходного понятия каких-либо признаков, составляющих видовое отличие обобщенных в этом понятии предметов, а ограничение – как переход к понятию с меньшим объемом за счет добавления новых признаков к видовому отличию исходного. Это лишь некоторые, наиболее простые, частные, случаи операций обобщения и ограничения понятий, а именно обобщение здесь – переход от понятия вида х(А(х) & В(х)) к понятию хА(х); ограничение – обратный переход. Например: «государство» – «европейское государство» – «современное европейское государство».

Однако расширение, усиление, обогащение содержания понятия может происходить отнюдь не только за счет добавления, как и ослабление содержания – не только за счет исключения каких-то имеющихся в нем признаков. Очевидно, что содержание понятия «вещество, не соединяющееся с соляной кислотой», слабее, чем содержание понятия «вещество, не соединяющееся ни с какой кислотой» (а объемы их, соответственно, в обратной зависимости). Хотя дело здесь, конечно, не в количестве признаков!

 

 

Говоря о последовательных обобщениях и ограничениях понятий, естественно поставить вопрос: есть ли пределы этих процессов? То есть, имеются ли пределы обобщения и ограничения того или иного определенного понятия? Что касается ограничения, то здесь вопрос как будто решается просто. В истории логики на него отвечали обычно так: «Предел ограничения – это индивид!» Пределами ограничения, например, понятия «человек», являются «Аристотель», «Сократ», «Ф. Бэкон» и т.п. Для понятия «страна» таковыми являются «Франция», «Англия» и прочие. Однако это не точно. Ибо «Аристотель», «Платон», «Франция» и т.п.– это не понятия (точнее,– не понятийные выражения, а собственные имена). Фактически, пределами ограничения являются единичные понятия. Для человека таковым может быть «основоположник логики». Образование же собственного имени из единичного понятия – это особая операция! Операция, если можно так выразиться, «извлечения предмета» из объема единичного понятия. Так, из объема понятия «основоположник логики» посредством оператора «тот, который» (?) образуем единичное описательное имя: «тот человек, который является основоположником логики». Соответствующее собственное имя – Аристотель.

Сложнее дело обстоит с вопросом о пределах обобщения. Здесь надо отличать вопрос о пределах обобщения отдельно взятого понятия (вне какой-либо системы знаний) от обобщения понятия в составе некоторой системы знания, в рамках некоторой теории. Например, рассматривая понятие «млекопитающее, живущее на суше», можем получить: «млекопитающее», «животное», «живое тело», «тело» и даже вообще – «нечто». Это последнее, по-видимому, и есть предел обобщения любого отдельно взятого понятия. В рамках же биологии пределом обобщения только что рассмотренного понятия было бы, очевидно, «живое тело»; переход к понятию «тело» означал бы выход за эти рамки, поскольку тела вообще и тем более «нечто» (!) не являются объектом изучения биологии. Таким образом, вопрос о пределах обобщения понятия в системе знания решается конкретно для каждой науки или теории.

Наконец, обратим внимание на различие процессов обобщения понятий и обобщение предметов того или иного класса или видов некоторых предметов при образовании понятий. Последнее связано с анализом самих предметов, с отвлечением от каких-то их свойств. Иначе говоря, это мысленная операция с самими предметами, а не с имеющимися уже понятиями. Умение обобщать предметы каких-либо классов, множеств является важным моментом научного познания, а также свидетельством «острого ума» и проницательности. Естественно, что этот прием заслуживает серьезного внимания в педагогической практике, так как связан с формированием и развитием творческих способностей мышления учащихся. Здесь речь идет о том, чтобы найти что-то общее в сугубо различных предметах. Так, в понятиях «симметрия», «система», «структура» обобщаются различные, весьма далекие, внешне не сходные объекты и их характеристики. Заметим, кстати, что именно умение осуществлять обобщения предметов подразумевается у представителей некоторых профессий, когда испытуемым предлагаются многообразные тесты типа: «Что общего между ботинком, книгой и телевизором? Между верблюдом, лампочкой и шариковой ручкой?»

 

Упражнения

 

1. Укажите, представляют ли указанные ниже последовательности понятий (или какие-нибудь их части) обобщение или ограничение понятий:

а) планета – планета Солнечной системы – ближайшая к Солнцу планета Солнечной системы;

б) младший лейтенант – лейтенант – младший офицер – офицер;

в) секунда – минута – час – сутки – единица времени;

г) абстрактная алгебра – алгебра – математика;

д) студент – человек – человечество;

е) созвездие «Малая медведица» – звезда «Малой медведицы» – «Полярная звезда»;

ж) число – четное число – число, которое делится на 2 или на 3 – число, которое делится на 2 и на 3;

з) глагол – слово изменяемое по лицам – изменяемое слово;

и) гражданин Польши – гражданин Польши и США;

к) окружность – геометрическое место точек – точка окружности – центр окружности.

2. Осуществите какие-нибудь обобщения и ограничения следующих понятий:

а) исторический роман;

б) тригонометрическая функция;

в) органическая кислота;

г) звук;

д) человек, знающий английский язык;

е) деятельность;

ж) человек, изучающий все славянские языки;

з) студент, который живет в Москве или Санкт-Петербурге;

и) учитель, преподающий логику и эстетику;

к) мужчина, любящий какую-нибудь женщину.

3. Укажите ближайший род для следующих видов (животных и предметов):

а) заяц, кит, олень;

б) лед, воск, дерево, металл.

4. Укажите общий род для следующих понятий:

а) склоняемая часть речи, спрягаемая часть речи;

б) село, деревня, хутор, аул, кишлак.

5. Укажите возможные понятия, в которых можно обобщить предметы: тряпка, циркуль, мел, транспортир.

Попытайтесь осуществить какие-нибудь обобщения и ограничения полученных понятий.

Деление понятий. Классификация

К операции деления мы прибегаем во всех случаях, когда возникает задача обзора, систематизации некоторого материала, определения последовательности планируемых действий. Конкретнее, в этих ситуациях речь идет об ответе на вопрос; какие виды, особые случаи предметов, явлений имеются среди предметов и явлений, обобщенных в некотором понятии? Сама же операция деления указывает, каким именно образом систематизировать эти обзоры. Ясно, что связанные с делением упорядочение, систематизация имеют важное значение в педагогическом процессе, в процессе изложения того или иного учебного материала таким образом, чтобы оно не было разрозненным, беспорядочным, несвязанным, а представляло бы собой определенную систему. Демонстрируя необходимую упорядоченность изложения материала, учитель прививает тем самым, конечно, соответствующие навыки и самим учащимся, вырабатывая у них необходимые элементы культуры мышления.

Наряду со значением в педагогической практике, деление имеет и определенное теоретическое значение. Обобщая предметы того или иного класса в понятии, мы фиксируем – как говорили ранее – нечто общее у предметов этого класса, отвлекаясь от всех видовых особенностей и индивидуальных различий предметов внутри этого класса. Так, образуя, например, понятие «металл» и фиксируя при этом то, что все металлы представляют собой химически простые вещества (то есть молекулы их состоят из однородных атомов) и что атомы их обладают низким коэффициентом ионизации, мы отвлекаемся от таких особенностей, которые характерны для цветных, щелочных металлов и отдельных металлов: натрия, железа, свинца и т. п. Однако, прибегая к такому отвлечению – необходимому на определенном этапе познания – мы вовсе не исходим из того, что видовые и индивидуальные различия предметов безразличны для науки. Наоборот, выявив нечто общее в предметах, наука стремится далее к конкретизации знания, именно: к выявлению особенного в общем. Это значит, что задача ее далее состоит в том, чтобы выявить возможные виды предметов данного рода. Достигается это в процессах деления.

Деление понятий – это операция разбиения объема понятия на подклассы, представляющие собой виды предметов, мыслимых в этом понятии (Разбиение класса (множества) – теоретико-множественная операция разделения множества на взаимно не пересекающиеся и непустые подклассы, объединение которых составляет исходное множество.). Строго говоря, как видим, делится не понятие, а объем некоторого понятия. Однако само выделение видов предметов осуществляется в соответствующих понятиях. Каждое такое понятие есть результат ограничения исходного. Таким образом, сам процесс деления понятия может быть охарактеризован, так же как процесс выявления возможных видовых понятий.

Как мы видим, процесс деления понятия имеет два аспекта: интенсиональный и экстенсиональный. Первый представляет собой выявление понятий, являющихся видовыми по отношению к исходному. Результатом является выделение видов предметов объема исходного понятия и осуществления таким образом разбиения его объема. Последнее и составляет второй аспект деления. Поскольку каждый вид предметов данного рода представляет собой нечто особенное в том общем, что зафиксировано в содержании понятия, деление понятия есть выявление возможных различий в составе его объема. При этом различение проводится всегда с какой-то точки зрения.

Признаки предметов, как мы видели, можно было различать по степени сложности, по содержанию и т.д. Людей, например, различают по возрасту, профессиям, по национальности, по классовой принадлежности и т. п. То, что мы называем точкой зрения или аспектом различения предметов, называют основанием деления понятий.

В дальнейшем мы выясним, что представляет собой основание деления с логической точки зрения.

Цель деления понятия состоит в том, чтобы выделить все возможные виды предметов каждый раз по некоторому определенному основанию. А это в свою очередь нужно для осуществления систематического обзора мыслимых в понятии предметов. К тому же, как можно установить из приведенных ранее характеристик развития понятия, деление понятия является одним из существенных этапов его развития. Осуществляется конкретизация понятия и раскрытие его содержания, если иметь в виду то, что мы ранее назвали полным содержанием понятия. Деление имеет тем большее гносеологическое значение, чем более существенными являются характеристики предметов, служащие основаниями деления. Вообще выбор основания зависит обычно от той познавательной задачи, в связи с которой возникает потребность деления понятий.

В составе каждого деления, имея в виду его интенсиональный аспект, можно выделять: делимое понятие А, основание деления, члены деления – В₁, В₂, ..., В_n –видовые понятия по отношению к исходному, выделенные по данному основанию. При экстенсиональной характеристике деления делимым является объем исходного понятия, а членами деления – его подклассы. При описании деления в одних случаях удобнее пользоваться терминологией, относящейся к его интенсиональной характеристике, в других – к экстенсиональной. Заметим, что каждое деление понятия является разбиением его объема, однако не каждое разбиение некоторого класса или множества предметов представляет собой деление некоторого понятия. Так, множество студентов некоторой учебной группы, состоящей, положим, из 20 человек, можно любым образом разбить на 4 группы по 5 человек, 5 групп по 4 человека и т.д., не интересуясь при этом какими-либо сходствами или различиями элементов исходного множества.

Различают правильное и неправильное деление. Деление является правильным, если оно удовлетворяет следующим пяти условиям, называемым в теории понятия также правилами деления:

(1) Деление должно происходить по одному определенному основанию.

Так, механическое движение А (рассматриваемое в некотором отрезке времени) мы можем разделить по характеру траектории (основание деления) на прямолинейное В₁, криволинейное В₂, колебательное В₃. В зависимости от изменения скорости во времени (другое основание деления) выделяем равномерное движение, равноускоренное, равнозамедленное.

Требование (1) не исключает того, что основание деления может представлять собой сочетание двух или даже большего числа различных признаков. Так, объединяя указанные основания деления механического движения, можем получить новое деление: механическое движение может быть прямолинейным и равномерным, прямолинейным и равноускоренным, прямолинейным и равнозамедленным, криволинейным и равномерным и т.д. Однако в предполагаемое продолжение мы не должны включать члены «колебательное и равномерное», как и «равноускоренное и равнозамедленное», поскольку таких случаев движения не существует в действительности, а между тем цель наша состоит в выявлении различий именно среди предметов, обобщенных в понятии. К тому же, включение таких членов противоречило бы и пониманию деления понятия как разбиения его объема.

(2) Полученные при делении понятия должны быть попарно-несовместимы.

(3) Члены деления как классы должны исчерпывать объем исходного понятия, то есть объединение их должно быть равно этому объему.

(4) Никакой из членов деления не должен быть пустым классом. Условия (3) и (4) объединяются обычно в виде одного требования – соразмерности деления.

(5) Деление должно быть непрерывным, то есть все его члены являются ближайшими видами объема исходного понятия, выделяемыми по выбранному основанию.

Это условие не выполняется, например, для деления понятия «член предложения» на «главный член предложения», «определение», «дополнение», «обстоятельство», поскольку «определение», «дополнение», «обстоятельство» не ближайшие виды с точки зрения роли членов предложения для данного понятия. Ближайшими же видами являются «второстепенные члены предложения». То же условие нарушится, очевидно, при делении членов предложения на «подлежащее», «сказуемое», «определение», «дополнение», «обстоятельство».

Нетрудно видеть, что условие (5) равносильно требованию: в процессе деления данного понятия должны выявляться (по данному основанию) в первую очередь ближайшие виды делимого понятия, далее, в случае надобности, ближайшие виды этих видов и так далее.

Очевидно, что условия (2) и (5) являются следствиями (1). Если выполнено первое, то само собой выполняются (2) и (5). Однако это верно лишь тогда, когда точно определено основание деления, что иногда бывает делать довольно трудно. Требования (2) и (5) в таких случаях являются полезными дополнительными критериями правильности деления. В частности, их нарушение в том или ином делении указывает как раз на нарушение условия (1). Следует заметить, кстати, что условия (1) и (5) связаны прежде всего с интенсиональной характеристикой деления как приема познания, тогда как (2), (3) и (4) являются следствиями понимания деления как разбиения класса.

Нетрудно видеть, что все указанные условия содержатся в более или менее явном виде в самом определении деления. В силу этого мы имеем понятие лишь правильного деления. Неправильное деление, по существу, не есть деление. При употреблении этого понятия в традиционной теории понятия вообще подразумевается, что имеется понятие деления, из которого в качестве его видов могут быть выделены правильное и неправильное деление. Однако не существует такого определения и не удается его сформулировать. Под неправильным делением мы просто подразумеваем здесь нечто похожее на эту операцию, или, точнее, наличие попытки ее осуществления, оказавшейся неудачной. Однако в силу сложившейся терминологической практики трудно избежать оборотов «правильное деление», «неправильное деление», и мы не будем во что бы то ни стало избегать их использования.

В учебниках логики обычно наряду с правилами деления говорят о возможных ошибках в делении – о возможных нарушениях тех или иных правил. Так, при нарушении условия (1) говорят, что деление «сбивчиво» или просто, «что деление происходит не по одному основанию» или происходит «смешение оснований».

Ошибка, связанная с нарушением (2), состоит в том, что «члены деления не исключают друг друга».

Невыполнение условий (3) или (4) влечет ошибку, характеризуемую как несоразмерность деления (отсутствие равенства между объемом делимого понятия и совокупностью членов деления). Причем, в случае нарушения (3) несоразмерность состоит в том, что деление оказывается «слишком узким», а невыполнение (4) означает, что деление является «слишком широким» (то есть в его состав включаются классы предметов, отсутствующие в объеме делимого понятия).

Наконец, нарушение условия (5) характеризуется как «скачок в делении».

С познавательной точки зрения заслуживают особого внимания возможные нарушения условий (1) и (5), а также условия (2), поскольку оно является следствием (1).

Если принять за деление перечисление, которое мы нередко слышим в метро: «У нас принято уступать места женщинам, детям и престарелым гражданам», то здесь очевидна ошибка, состоящая в смешении оснований, следствием которой является здесь – и обычно – также и то, что члены деления не исключают друг друга. Однако не каждое перечисление видов того или иного рода является делением соответствующего понятия.

Перечисление может ставить целью просто выделение каких-то членов класса наиболее существенных или вообще интересующих кого-либо с какой-то точки зрения. Ясно, что в этом случае неполнота не является ошибкой, а перекрещивание подклассов также недопустимо, если оно не чревато какими-либо ошибками в решении задач, которые имеются в виду. Иногда перекрещивание понятий – членов указанного перечисления – не так уж и плохо. Если пассажир – женщина и к тому же престарелая, то по отношению к ней надо быть вдвойне вежливым!

Можно также привести следующий пример перечисления, которое представляется на первый взгляд неправильным делением. Так, в отчете одного из руководителей прокуратуры сказано: «В прошлом году по инициативе прокуроров восстановлено 11 тысяч незаконно уволенных. Удовлетворено 90 тысяч жалоб граждан. Наказано 18 тысяч должностных лиц, 32 тысячи привлечены к материальной ответственности...» Здесь уже обращает на себя внимание перекрещивание членов перечисления и, даже, возможно, имеется неполнота перечисления видов работы – подклассов объема понятия «мероприятия прокуратуры по соблюдению закона о порядке обжалования неправомерных действий должностных лиц».

Судя по всему, автор отчета и не ставил задачу систематического обзора всех видов мероприятий указанного класса. Цель состояла, по-видимому, в выделении наиболее существенных. Однако здесь перекрещивание может иметь неприятные последствия, особенно если кто-то захочет воспользоваться цифрами отчета. В частности, нельзя, например, ответить на вопрос: входят ли 18 тысяч наказанных должностных лиц в число 32 тысяч, привлеченных к материальной ответственности? И уж явно возникают недоразумения относительно числа при прочтении сообщения работника МВД: «За истекший период сотрудниками нашего отдела было изъято: 8 единиц холодного оружия, 4 пистолета ПМ, 2 финских ножа, 10 единиц огнестрельного оружия, 3 кастета и 2 ружья марки ТОЗ». Здесь возникают многочисленные вопросы, остающиеся без ответа: сколько всего оружия было изъято? И главное – в силу перекрещивания членов «холодное оружие», «финский нож», «кастет» – неясным оказывается вопрос о том, входят ли в число холодного оружия ножи и кастеты? По тем же причинам неясен аналогичный вопрос и об огнестрельном оружии.

Деление применяется с целью обеспечения систематического и полного обзора возможных видов предметов рода. Обзор такого рода связан с некоторой задачей, и потому в качестве основания деления выбирается каждый раз нечто существенное для решения этой задачи. Смешение оснований в делении лишает обзор систематичности. Обычно возникающие при этом следствия, состоящие в том, что члены деления не исключают друг друга, может оказаться особо недопустимым, когда рассматриваемая задача имеет различные решения для предметов различных видов. В связи с этим ясно требование, чтобы члены деления исключали друг друга.

При известном способе доказательства, например, теоремы о том, что каждый вписанный в окружность угол измеряется половиной дуги, на которую он опирается, существенным оказывается деление всех вписанных в окружность углов в зависимости от того, расположен ли центр окружности на линии, соединяющей концы отрезков (сторон) угла, выше этой линии (то есть внутри образованного треугольника) или ниже нее (вне треугольника).

При определении правил расстановки знаков препинания в конце предложений существенно различение предложений как по их содержанию (повествовательные, вопросительные, побудительные), так и по интонации (восклицательные и невосклицательные, то есть произносимые спокойным тоном). Насколько важно правильно произвести в этом случае деление, можно показать на одном примере из учебника грамматики.

Авторы делят предложения по разным основаниям, в частности по содержанию (по цели высказывания): на повествовательные, вопросительные и побудительные; затем по интонации (эмоциональной окраске): на восклицательные и невосклицательные (произносимые спокойным тоном). Правда, авторы выделяют только восклицательные, подчеркивая, что «любое предложение: повествовательное, вопросительное или побудительное – может стать также и восклицательным», не учитывая, что в каждом роде есть, по крайней мере, два вида. При наличии восклицательных имеются и невосклицательные, которые, конечно, подразумеваются.

При формулировке правил расстановки знаков в конце предложений осуществляется новое деление, в котором происходит смешение указанных оснований. А именно: правила формулируются следующим образом: в конце повествовательного предложения ставится точка, в конце вопросительного – знак вопроса, а в конце восклицательного – знак восклицания. Следствием смешения оснований в осуществляемом здесь делении предложений (на повествовательные, вопросительные и восклицательные) является также и то, что члены деления не исключают друг друга. В результате у читателя, естественно, возникают вопросы, какой знак надо ставить после предложения, которое является повествовательным и в то же время восклицательным, после вопросительного и в то же время восклицательного, побудительного и в то же время восклицательного? Но, по-видимому, деление в последнем случае должно было бы быть осуществлено по сложному основанию – содержанию и тону (повествовательные-восклицательные, повествовательные-невосклицательные и аналогично – для побудительных), поскольку постановка знаков препинания зависит как от той, так и другой характеристик предложений.

Следствием нарушения, как уже сказано, условия (5) является ошибка, которую называют скачком в делении. При этом, как можно заметить из приведенных примеров (см. примеры к условию (5) – деление членов предложения), существуют две разновидности этой ошибки. В одном случае – в первом примере – вместо указания некоторого члена деления мы осуществляем его подразделение, то есть совокупность его видов. Во втором случае – в другом примере – вместо перечисления ближайших видов делимого понятия происходит перечисление видов этого последнего. В обоих случаях нарушается взаимосвязь (диалектика) сходного и различного, общего и особенного: в результате скачка перечисляются различия (в объеме данного понятия) без выявления тех сходств, в рамках которых они имеют место.

Виды деления. Операция деления объема понятия на виды, в свою очередь, имеет различные виды. В основном они выделяются по характеру оснований деления. Как мы уже видели, основание может быть простым и сложным (сочетанием нескольких простых оснований). В соответствии с этим простым или сложным может быть само деление. Возможны и более принципиальные различия. До сих пор мы рассматривали деления, в которых основание представляет собой некоторую предметно-функциональную характеристику, проще говоря, предметную функцию более или менее сложного характера, определенную на множестве предметов, составляющих объем делимого понятия. Таковы, например, содержание (или цель) предложения, структура предложения, соотношение сторон треугольника и т.п.

Особый характер функции здесь часто выражается в специфике их возможных значений. Значениями последней функции являются, например, «попарное неравенство всех сторон треугольника», «равенство двух сторон треугольника», «равенство всех трех сторон». Соответственно этому деление треугольников по соотношению сторон приводит нас к видам: разносторонние, равнобедренные и равносторонние треугольники. Обычно значениями предметной функции, которая выбирается в качестве основания того или иного деления, являются различные свойства – или признаки вообще – предметов, и членами деления тогда являются виды, различающиеся как раз этими свойствами, например, значениями функции «агрегатное состояние тела» – это «твердое», «жидкое», «газообразное» и «в состоянии плазмы». Результатом деления тел по агрегатному состоянию тогда будет перечень: твердые, жидкие, газообразные и находящиеся в состоянии плазмы.

Можно взять, конечно, в качестве основания деления и обычную числовую функцию, представляющую собой ту или иную количественную характеристику предмета, например, рост (применительно к человеку, то есть определенный на множестве людей). Если при этом множество возможных значений функции включает какие-то качественные градации роста (низкий, средний, высокий) или какие-то числовые градации, то согласно этому множеству значений мы можем получить множество видов людей, как результат деления людей по данному основанию.

Рассмотренный вид деления называют делением по видоизменению некоторого признака (название, как нетрудно видеть, не вполне соответствует сущности деления, однако трудно подобрать что-нибудь другое, более подходящее).

Деление другого вида носит название дихотомического. В качестве основания здесь – точка зрения, исходя из которой мы выявляем видовые отличия внутри рода,– принимается наличие или отсутствие некоторого заданного свойства. В зависимости от наличия или отсутствия кристаллической решетки у твердых тел, мы делим их на кристаллические и некристаллические. Аналогично получаем деление механического движения на равномерное и неравномерное; предложения на повествовательные и не повествовательные и т.д.

Дихотомические деления также могут быть простыми (как в приведенных примерах) и сложными – когда основанием деления является наличие или отсутствие каждого из свойств некоторого множества. Студентов мы можем таким образом разделить на: способных и трудолюбивых; способных, но не трудолюбивых; неспособных, но трудолюбивых; неспособных и нетрудолюбивых.

Примерами сложных дихотомических делений являются приведенные в своем месте разбиения объемов понятий с помощью диаграмм Венна, а также дизъюнктивные разложения объемов.

Недостатком дихотомических делений, по сравнению с рассмотренным выше видом, является их недостаточная конкретность – неопределенность отрицательных их членов. Но они применяются обычно именно в тех случаях, когда существенно выделить предметы, обладающие некоторым свойством. Преимуществом их является большая простота самой операции, гарантирующая, в частности, от таких ошибок, как перекрещивание членов деления, то есть случаев, когда члены деления не исключают друг друга. В простых дихотомических делениях, казалось бы, всегда обеспечена и соразмерность, поскольку объединение объемов противоречащих понятий  являющихся здесь членами деления, всегда равно объему родового (делимого) понятия. Однако множество  может быть пусто! Как, например, в делении кристаллических веществ на имеющих определенную температуру плавления и не имеющих такой. Деление, очевидно, содержательно неправильно.

«Дихотомическое» буквально означает двучленное, но не всякое двучленное деление является дихотомическим. Явно не дихотомично деление людей на мужчин и женщин или планет (Солнечной системы) на большие и малые. Дихотомическое деление – это именно особый способ деления. Дихотомически мы разделили бы людей на мужчин и не мужчин, планеты (Солнечной системы) – на большие и небольшие (здесь отчетливо выявляются недостатки таких делений – неопределенность отрицательного члена – и их достоинства – отсутствие необходимости уточнять состав объема делимого понятия дополнительно к той, которая выделяет положительный член).

Обратим внимание читателя на то, что деление такого рода может быть использовано как средство выявления и воспроизведения некоторой информации. Например, при опросе очевидцев того или иного события, допросе свидетелей по какому-нибудь уголовному делу и т.п. Предположим, свидетель по делу об ограблении, присутствовавший в момент ограбления и видевший грабителя, не помнит, как он выглядел, в чем был одет и т.д. Для того, чтобы помочь ему вспомнить это, как раз и полезно прибегнуть к дихотомическому делению. Он не помнит, в частности, цвет пальто на грабителе. Вы задаете ему вопрос, было ли на нем красное пальто или нет? Скорее всего он ответит «нет». Далее, желтое или нежелтое? Опять оказывается «нет». Белое или небелое? Синее или нет? И так до тех пор пока он не вспомнит, что оно было коричневое... Конечно, можно вести такое деление по самым разным признакам: относительно вида и цвета одежды, что находилось в руках и т.д., и т.п.

Каждый студент, который сдавал какой-нибудь экзамен, не очень хорошо зная предмет, может, вероятно, вспомнить, что к этому приему прибегал экзаменатор, задавая так называемые наводящие вопросы: является ли эта функция алгебраической или нет, а может быть тригонометрической? Было ли это событие до или после войны 1812 года? До или после отмены крепостного права? и т.д. В подобных случаях дихотомическое деление играет роль мощного логического средства побуждения человека к воспроизведению и анализу ранее воспринимаемых ситуаций и сведений.

КЛАССИФИКАЦИЯ

С приемом познания, который называют классификацией, знаком, вероятно, более широкий круг людей, чем с операцией деления понятий. Однако классификация есть не что иное, как либо отдельное деление, либо совокупность делений (деление объема некоторого исходного понятия, затем полученных при этом членов и т.д.).

Не существует, однако, общепринятой характеристики классификации как особого вида деления (дающей основание для употребления особого термина для этой операции). Различие между тем, что мы называем просто делением, и теми делениями, что называют классификациями, состоит, по-видимому, в том, что в одном случае операция деления применяется в некоторой ситуации, в рассуждении в связи с решением той или иной частной задачи, поэтому результаты его не фиксируются и не сохраняются специально в общем фонде человеческих знаний. Деления такого рода можно назвать рабочими делениями. Классификацией называют обычно деление, относящееся к классам объектов, которые являются предметами изучения той или иной науки. Сравните классификацию суждений и понятий в логике, предложений – в лингвистике, животных и растений и вообще живых тел – в биологии, общественно-экономических формаций – в историческом материализме, химических элементов – в химии. В этом случае деления, точнее, их результаты постоянно используются в науке, имеют непреходящий характер. Такой же характер имеют классификации книг в библиотеках, классификации инструментов на складах и т.п.

Различия между рабочими делениями и классификациями можно обнаружить еще и в том, что в последних не применяют обычно приемов дихотомического деления. Как уже отмечалось, деление объема понятия на виды, а значит, и классификация тех или иных предметов осуществляется по более или менее существенным характеристикам (признакам) предметов. Однако, как мы уже знаем, признаки могут быть существенными для предмета (определяющими его качественную специфику или хотя бы обусловливающими какие-то другие признаки) и существенные в каком-то отношении предмета с другими предметами, в частности, при том или ином его употреблении. В зависимости от того, какого именно рода – с точки зрения существенности – признаки используются в классификации, различают классификации естественные и искусственные. Классификации множеств объектов той или иной науки являются обычно естественными; таково же деление книг в библиотеке по отраслям знаний, но сортировка книг по буквам фамилий их авторов является явно искусственным их делением, хотя ясно, что для определенных целей оно может быть даже необходимым. Но речь идет не о целях познавательного характера. С точки зрения интересов познания предметов важны именно естественные классификации. Обычно каждая рубрика естественной классификации является концентратом определенных знаний о входящих в нее предметах.

В качестве примера естественной классификации особо выделяют обычно классификацию химических элементов таблицы Менделеева. С каждой рубрикой, выделяющей отдельный элемент, ряд или столбец этой таблицы, как мы знаем, связана определенная совокупность знаний о соответствующих химических элементах. В силу этих особенностей естественной классификации, отнесение предмета к тем или иным рубрикам дает возможность перенести на него все накопленные уже знания.

КЛАССИФИКАЦИЯ И ХАРАКТЕРИСТИКА ПРЕДМЕТОВ

Упомянутые знания, которые могут быть перенесены на предмет, отнесенный к некоторой рубрике естественной классификации, представляют собой некоторую систему, которую можно назвать характеристикой предмета. Эта система суть множество значений предметных функторов – оснований классификации. Сама эта совокупность функторов есть схема характеристики. Она же – структура классификации, которая определяется множеством тех предметно-функциональных характеристик предметов, которые служат основаниями делений (делений и подразделений), составляющими данную классификацию. Упомянутая схема характеристики предмета – это своего рода фрейм – набор тех существенных рубрик, которые следует запомнить, чтобы получить характеристику предмета. Вспомним, что набором предметно-функциональных параметров, составляющих схему принятых у нас характеристик людей, являются: «фамилия», «имя», «отчество», «год рождения», «место рождения», «национальность», «занимаемая должность», «отношение к делу», «отношение к товарищам и товарищей к нему», «степень нравственной и политической зрелости». Сама характеристика человека есть перечень значений указанных функций.

Для каждой рубрики естественной классификации точно определен перечень таких функций и множество соответствующих значений.

 

ТАКСОНОМИЧЕСКИЕ И МЕРЕОЛОГИЧЕСКИЕ ДЕЛЕНИЯ И КЛАССИФИКАЦИЯ

Наряду с рассмотренными способами деления и, соответственно, классификаций, издавна описанными в логике, которые называют иногда таксономическими, в последнее время находят широкое применение, например, при описании объектов в диалоговых системах, в языках, предназначенных для непосредственного общения человека с компьютером, морфологические классификации. Для процедур, которые имеются здесь в виду, правомерно употреблять также термин мереологическое деление. В отличие от таксономического деления, в процессе которого выявляются виды предметов некоторого рода, мереологическое деление есть расчленение некоторого предмета на части. Скажем, например, что самолет состоит из частей; крылья, фюзеляж, мотор, управляющая система, шасси. Ясно, что каждую из частей можно подразделить в свою очередь на части.

Операцией, сходной с этой, является также выделение некоторых характеристик предмета типа предметно-функционального характера. Например, основными характеристиками крыла самолета являются форма в профиле, форма в плане, длина, ширина и т.д.

Теория мереологических классификаций требует еще разработки. Не ясно, можно ли, и если да, то в каком смысле, говорить об основаниях деления и классификации, о существенности и несущественности их, правилах и возможных ошибках в этих операциях. Укажем лишь на некоторую связь между мереологическим и таксономическим делением (учитывая которую можно, вероятно, пролить некоторый свет на указанные вопросы).

Связь состоит в том, что каждое мереологическое деление превращается в таксономическое деление, если вместо имени расчленяемого предмета а употребить понятие «часть предмета а». Например, части самолета – крылья, фюзеляж и т.д. Части предмета, то есть члены мереологического деления, становятся в таком случае видами исходного понятия. (Заметим, кстати, что при этом исключаются, очевидно, дихотомические деления.)

Однако расчленение предмета с точки зрения цели, ради которой оно осуществляется, едва ли сводится к обзору видов его частей. Существенным здесь является представление предмета как некоторой системы, в связи с чем важное значение имеет различение частей по их функциям, учет их связей в составе целого и т.д. Типичным примером расчленения является составление плана некоторой работы (учебника, монографии, сочинения вообще). И здесь важно выделить основные вопросы и проблемы, а также подчиненные им в некотором смысле подпроблемы данной проблемы, подвопросы. Важно предусмотреть правильную последовательность или, как говорят, логичность изложения материала.

 

Упражнения

 

1. Проанализируйте следующие деления понятий. Установите, по каким основаниям они произведены, что в них является делимые понятием и членами деления, убедитесь в их корректности, то есть удовлетворяют ли они сформулированным выше требованиям (правилам):

а) Прогрессии бывают арифметические и геометрические. Арифметические могут быть с положительной и отрицательной разностью. Геометрические – с целыми или дробными (несократимыми) знаменателями;

б) Зубы у человека бывают передние, задние, верхние, нижние, резцы, клыки, молочные и зубы мудрости, а также зубы, подверженные кариесу;

в) Изменяемые части речи – это части речи, изменяющиеся по падежам, по числам, временам и лицам;

г) Множество работников некоторого отдела можно разбить на следующие типы лиц. уравновешенные, склонные к противоречию, цельные, с аналитическими способностями, владеющие собой, безынициативные;

д) Дивизии, как известно, делятся на пехотные, авиадесантные, моторизованные, а также на полки, батальоны, роты, взводы и отделения;

е) С точки зрения криминологии важно принимать во внимание следующие типы преступных группировок: устойчивые, менее устойчивые, случайно сформированные и быстро распадающиеся.

2. Выявите имеющиеся ошибки в приведенных ниже делениях и попытайтесь их исправить, осуществив правильные деления по соответствующим основаниям:

а) Транспорт бывает воздушный, морской, речной, подземный, сухопутный, железнодорожный, автомобильный и гужевой;

б) Треугольники бывают прямоугольные, тупоугольные, равноугольные, остроугольные, равнобедренные, равносторонние.

3. Установите, в каких из примеров имеет место деление понятий, а в каких – мысленное расчленение предмета на

части. Покажите, как можно превратить расчленение в деление, изменив исходное понятие:

а) Обед состоял из первого, второго и третьего;

б) Алфавит состоит из букв, представляющих звуки и указывающих на характер произношения звука;

в) Институты имеют очные, вечерние и заочные отделения;

г) Студенты делятся на студентов-очников, вечерников и заочников.

4. Осуществите какие-нибудь деления понятий:

а) журнал;

б) смех;

в) управление;

г) любовь;

д) учреждение;

е) глагол;

ж) здание;

з) химический элемент;

и) элементарная частица;

к) литература.

 ОПРЕДЕЛЕНИЕ (ДЕФИНИЦИЯ) КАК ПРИЕМ ПОЗНАНИЯ

§ 24. Общая характеристика определения

Операция определения является одной из наиболее важных в процессе познания. Она связана с основной проблемой, определяющей роль языка как средства коммуникации и познания, а именно,– с проблемой связи выражений языка с объектами, которые эти выражения должны представлять как знаки. Другими словами, операция определения связана с проблемой формирования предметных значений знаков языка, а вместе с этим и смысловых значений выражений языка. Отсюда возникает связь рассматриваемой операции с тем, что обозначают в педагогике словами «понимание», «уяснение смысла», «сознательное усвоение учебного материала», «механическое запоминание» или злосчастная «зубрежка». Каждый, кто оглянется на свое школьное прошлое, вспомнит, вероятно, что ни одно доказательство, ни одно опровержение не обходится без определений. Наличие определений основных терминов доказательства – необходимое условие его осуществления. От наличия более или менее ясных определений терминов в том или ином изложении материала зависит ясность и точность этого изложения.

К сожалению, надо заметить, что в логике и эпистемологии до сих пор не было точного и до сих пор нет общепринятого определения самого термина «определение», а это значит, не ясно, что имеется в виду под данным термином, и все разговоры в таком случае могут превратиться, по словам одного мыслителя, в «шелуху слов» вместо мыслей.

Эту операцию характеризуют обычно как операцию, посредством которой раскрывается содержание понятия. Однако, как мы видели, понятие всегда характеризуется наличием какого-то содержания. «Понятие, содержание которого не раскрыто» – это просто не понятие. А если оно уже имеется, то зачем его раскрывать? При более точной трактовке определения, как приема познания, оно скорее есть способ введения понятий в науку, хотя и эта характеристика не может быть отнесена ко всем определениям вообще. Но во всяком случае здесь речь идет уже не об операциях с понятиями. Эта операция со словами, с выражениями языка. Основная цель, которой она подчинена,– обеспечение точных предметных значений слов языка как знаков. Поэтому она имеет большое значение для обеспечения определенности нашего мышления в той части, которая зависит от определенности предметных значений языковых знаков. Последние определяются как раз для того, чтобы предотвратить такие ситуации, когда знаки отрываются от их предметных значений, мышление лишается предметного содержания и превращается в пустое словотворчество. Таким образом, от определений зависит точность нашего мышления. Как метко заметил английский естествоиспытатель XIX века Д. Гершель: «Нельзя внести точность в рассуждения, если она сначала не введена в определения».

• ОПРЕДЕЛЕНИЕ есть логический способ установления или уточнения связи языкового выражения с тем, что оно обозначает как знак языка. Этот способ состоит в придании выражению некоторого смысла (или уточнении, углублении имеющегося смысла), который выделяет то, что должно быть предметным значением данного выражения. Выражение языка, к которому относится определение, называется определяемым. Знаковая форма, выражающая смысл придаваемый определяемому, называется определяющим. Определяемое иначе называют дефиниендум, а определяющее – дефиниенс.

Для понимания специфики определения как приема познания полезно вспомнить основные типы языковых выражений (см. § 2) и учесть, что определяемыми могут быть выражения различных синтаксических категорий: именные формы (единичные, общие имена и общие формы применения предметных функторов) и высказывательные формы (предложения и предикаты).

 

Примеры

 

1. «Полярная звезда» – это та звезда, направление на которую из любой точки земного шара, с которых эта звезда видна, есть направление на север». Определяемым здесь, очевидно, является единичное имя «Полярная звезда».

2. Определение общего имени:

– «Точка зенита небесной сферы – это высшая точка над головой наблюдателя».

– «Sin(x) – это число, равное отношению длины катета, противолежащего углу х, к гипотенузе прямоугольного треугольника» (где область D для х – множество острых углов прямоугольного треугольника) – определяемое здесь, очевидно,– общая форма применения предметного функтора «синус». Это определение отличается от определения «sin», представляющего имя функции, которую (опять-таки применительно к множеству острых углов прямоугольных треугольников) можно определить как «функцию, которая соотносит каждому углу (из указанной области) число, равное отношению длины соответствующего катета к длине гипотенузы».

– «х больше у, если и только если существует такое z, что х = у + z» – определяемое здесь выражение – предикат (применительно к области натуральных чисел в качестве возможных значений переменных).

Смысл, который приписывается в определении предложения,– это суждение или, поскольку оно выражено в определенной знаковой форме,– высказывание. Этот смысл указывает условия истинности предложения, а тем самым детерминирует (определяет) его предметное значение. Примеры определений предложений рассмотрим ниже. Сейчас заметим, что потребность в определении какого-то предложения возникает каждый раз, когда нам не ясен смысл утверждения, высказывания. Возникает, например, вопрос, что означает утверждение: «Всякое кристаллическое вещество имеет определенную температуру плавления»? Во время экзаменов, когда студенту ставят заниженную, по его мнению оценку, и он считает, что хорошо знает предмет, преподавателю нередко приходится разъяснять, что означает утверждение: «Студент хорошо знает предмет».

Из приведенных примеров читателю должно быть ясно, что определяемое и определяющее выражения относятся к одной и той же синтаксической категории выражений. Точнее говоря, определяющее именно и указывает категорию того, что определяется.

Кроме того, важно отметить, что определение единичных и общих имен непосредственно представляет собой способ «введения понятий в науку», поскольку, как не раз было сказано, именно понятия составляют смыслы имен – единичных и общих. По существу, это относится и к определению предикатов и к определению именной формы, ибо предикат А(х₁, ..., х_n) (n ≥ 1), который здесь приписывается в качестве смысла, представляет собой содержание понятия вида (х₁, ..., х_n) A(х₁, ..., х_n). А выражение fⁿ(х₁, ..., х_n) – составляющее смысл, приписываемый именной форме – является существенной частью содержания понятийной формы вида x(x = fⁿ(х₁, ..., х_n))(число х, равное fⁿ(х₁, ..., х_n)). Ясно, что при определенных значениях x_v ..., х_п эта понятийная форма превращается в понятие. «Определить некоторое выражение» буквально (например, в польском языке) означает «определить», то есть установить границы его применения. Однако, поскольку в определении мы приписываем смысл термину, то тем самым характеризуем предметы (определяем предметы). Более того, под определением термина мы имеем в виду именно указание характеристик предметов, которые он обозначает или должен обозначать. Определяя квадрат, мы характеризуем его как равносторонний прямоугольник. Но определяя термин «квадрат» в буквальном смысле, мы должны были бы сказать, что это есть слово, служащее для обозначения равносторонних прямоугольников.

Возможны, по крайней мере, три типа ситуаций, в которых возникает необходимость в определении:

1. В процессе развития некоторой науки или изложения научного материала в ходе некоторой аргументации, например доказательства какой-то теоремы, вводится новая языковая форма – термин, высказывательная форма и т.п. Естественно, при этом должно быть установлено, что именно он должен представлять как знак, что имеется в виду или что хотят иметь в виду при его употреблении. Так, при описании формализованного языка логики вводят понятие терма, формулы данного языка, свободной и связанной переменной. Физик, формулируя закономерности движения, вводит термины: скорость, ускорение, траектория и т.д. Ясно, что изложение может быть понятным другому – читателю, слушателю,– если он знает, что имеется в виду под каждым выражением употребляемого языка. Поэтому введение каждого нового термина сопровождается разъяснением.

Обычно это делается в форме: «Ускорением движения в данный момент времени называют (или «будем называть») предел отношения приращения скорости в течение некоторого отрезка времени к самому этому отрезку времени при стремлении этого отрезка к нулю (говоря математическим языком, ускорение в данной точке времени есть значение – в этой точке времени – производной скорости по времени)». Впрочем, вместо «ускорением называют отношение...» может быть просто «ускорение есть отношение...», иногда с добавлением «по определению», что чаще всего просто подразумевается в силу характера контекста, в котором дается определение. Желая иметь примеры определений, читатель может вернуться хотя бы к тем частям данной работы, где разъясняются смысловые значения упомянутых выше логических терминов (терм, формула, связанная, свободная переменная и т.п.). Но каждый, вероятно, помнит многие из определений, с которыми встречался в школе: «Параллелограммом называют четырехугольник с равными противоположными сторонами», «Корень слова – это неизменяемая часть данного слова», «Остров есть часть суши, окруженная со всех сторон водой».

2. Ситуация другого типа состоит в том, что для специальных целей науки используется некоторый термин или языковый знак вообще, который имеет употребление либо в других областях знания, либо в повседневном обиходе, но при этом употребляется в различных значениях, или, наконец, в данном употреблении его хотят использовать некоторым специальным образом. Так, слово «интерпретация» употребляется весьма часто в повседневной жизни и в разных случаях ему придается различный смысл, а чаще всего никакого определенного (в силу чего расплывчатый смысл имеют и утверждения, в которых речь идет об интерпретациях, то есть некоторых событий или каких-то выражений художественных или музыкальных произведений и т.д.). При описании формализованного языка, как мы видим, посредством определения термину «интерпретация» придан определенный смысл, а значит, и предметное значение.

3. В ситуациях третьего типа мы имеем дело с выражением, для которого уже в самой языковой практике установилось определенное, практически точное предметное значение. И задача, которую имеют в виду, применяя к такому термину определение, состоит в том, чтобы придать этому термину определенный смысл, а значит обеспечить и большую надежность и строгость в его употреблении. Так, практически каждый знает, какие существа называются словом «человек», что означает «болезнь», «производительность труда» и т.д. Однако интуитивное употребление термина оказывается недостаточным в некоторых особых ситуациях, когда нужно, например, доказать или опровергнуть утверждение, что некоторые предметы или явления относятся именно к тому классу предметов, который представляет данный термин: доказать или опровергнуть, например, что тот или иной человек действительно болен.

Читатели известной книги Веркора «Люди или животные» помнят, конечно, характер показанной там ситуации, в которой жизненно важным оказалось точное решение вопроса о том, что же такое человек.

Заметим, что функции определения в ситуациях (1) и (2) существенно отличаются от той, которую она имеет в ситуации (3). В ситуациях (1) и (2) мы имеем так называемые номинальные определения. Такое определение есть условие, соглашение относительно употребления данной знаковой формы. Иначе говоря, определение в этом случае представляет собой ответ на вопрос, что имеют в виду или будут иметь в виду под данным выражением (что называют или будут называть данным термином, что мы имеем в виду, употребляя данное выражение языка).

Хотя результат определения здесь и выражается в форме, сходной с повествовательным предложением, она не содержит какого-либо утверждения, кроме именно того, что данную знаковую форму предлагается употреблять так-то и так-то. Однако эта форма может быть использована в аргументации как повествовательное предложение, истинное по соглашению, именно по определению. По принципу предметности утверждение при употреблении некоторого знака относится к тому, что оно обозначает. Но в данном случае задача состоит как раз в том, чтобы установить, что именно должно обозначать определяемое выражение как знак. Существует афоризм – «Об определениях не спорят». Это относится именно к номинальным определениям. Если какой-то спор здесь и возможен, то лишь о том, целесообразно ли указанное в определении употребление термина или о том, насколько целесообразно введение самого понятия, которое ассоциируется с данным термином. Вопрос же о целесообразности введения какого-то понятия решается в связи с теми практическими и теоретическими задачами и потребностями, с которыми связано само введение термина и соответствующего ему понятия.

Понятие, которое вводится посредством номинального определения термина может сохраняться при дальнейших изменениях наших знаний о предмете, при возникновении более глубоких понятий о нем, в частности, при переходе от одной теории к новой теории, возникающей в результате углубления нашего знания, с которым связано изменение реальных определений. Именно благодаря такому сохранению некоторых понятий, то есть благодаря существованию транстеоретических понятий, создается преемственность в развитии знания. Развивая наши знания, мы не теряем из виду тех предметов, к которым относится наше познание. На них именно и указывают номинальные определения Так при переходе от механики Ньютона к релятивистской механике изменяются понятия (наши знания) «массы», «длины», «времени» и др. Мы узнаем, например, что масса зависит от скорости – увеличивается с увеличением скорости движения тела. Однако и в той, и в другой теории мы можем иметь в виду, а ученые очевидно имеют, под термином «масса» способность тела сопротивляться изменению скорости. Определение может сохраниться даже при переходе от релятивистской к какой-то другой механике, поскольку объектом изучения будет оставаться все та же способность тел сопротивляться ускорению.

Определения в ситуации (3) называют реальными. Другое, распространенное в литературе название этих операций – экспликация. Результат определения такого типа представляет собой суждение – характеристику обозначаемых данным термином предметов. В силу этого здесь возникает вопрос о его истинности или ложности и, естественно, возможны Споры относительно самого определения. Имеются, например, различные попытки определения «болезни», но никакое из них не является пока общепризнанным. Известны также продолжающиеся на протяжении многих веков споры о том, что такое человек.

Относительно реальных определений в свою очередь имеются две возможности с точки зрения применяемых к ним требований. Иногда, ставя вопрос, например, о том, что такое человек, имеют в виду указание какой-либо отличительной совокупности признаков человека. Такому требованию удовлетворяет, очевидно, определение человека, предложенное еще в Древней Греции, как существа от природы двуногого и бесперого. Возможно также определение его как существа, обладающего способностью плакать (имея в виду эмоциональный плач, а не просто рефлекторное выделение слез, которое возможно у многих животных). Однако под реальным определением имеют в виду ответ на вопрос, что представляют собой предметы по существу, в чем состоит основа их качественной специфики? Исходя из этого, указанные определения человека не считаются удовлетворительными как реальные определения. Среди философов распространено определение человека как продукта определенной совокупности общественных отношений. Хотя сама по себе эта характеристика, будучи существенной, не является его определением, поскольку к числу людей, без сомнения, относят и Маугли. По-видимому, наиболее точным образом человек может быть определен как член сообщества, производящего и использующего в своем взаимодействии с природой орудия труда. А членом сообщества является, очевидно, каждый, кто рожден членом этого же сообщества.

Из только что сказанного о реальном определении в строгом смысле ясно и то, что оно может относиться к классу предметов, уже обобщенных в том или ином понятии, но не выражающих сущность этих предметов. Есть ли, например, у нас понятие смешного? Очевидно, да. «Это все то, что вызывает смех». Но в науке нет пока ясности в том, в чем сущность смешного, каковы именно те признаки явления, в силу которых они способны вызывать смех. Говорят, что это некоторое несоответствие, но несоответствие может быть не только причиной смеха, но и слез. И остается еще задачей определить специфику несоответствия, противоречия, вынуждающих людей смеяться.

Характеристика того или иного определения как номинального или реального зависит, как мы видели, от того, какую функцию или задачу оно выполняет. А это в свою очередь определяется ситуацией, в которой применяется определение. Многие номинальные определения являются таковыми для читателей и слушателей, для которых предназначено изложение некоторого научного материала, но не для самого автора. Прежде чем сообщить слушателю или читателю о том, какие предметы будет обозначать вводимый термин, автор уже имеет в виду так или иначе выделенный класс предметов и должен для себя ответить на вопрос о том, как эти предметы могут быть охарактеризованы, то есть составить понятия о них. Это означает, что сам он вырабатывает реальные определения предметов.

 

Виды определений

По существу, мы уже выделили виды определений, различающихся по типам определяемых выражений. Кроме того, два вида определений – номинальные и реальные – уже выделены по тому, какую функцию выполняет определение, на какой вопрос оно дает ответ. Далее по структуре выделяют определения явные и неявные в зависимости от того выделяются ли в качестве самостоятельных (непересекающихся) частей определяемое выражение и определяющее. Все приведенные выше определения являлись явными Они имеют форму равенства, если определяемым выражением является та или иная именная форма,– или эквивалентности, когда определяемое есть высказывательная форма. Отношение равенства в естественном языке обычно выражается словами «это», «есть», «это есть» или «то же, что», а эквивалентности – словосочетанием «если и только если» или «равносильно», «означает то же, что».

Однако не каждое определение, имеющее форму равенства или эквивалентности является явным. Как мы увидим далее (см. контекстуальные определения), есть определения, имеющие форму равенства или эквивалентности, но не являющиеся явными. Определяемое и определяющее выражения в таких определениях не выделяются в качестве самостоятельных частей. Левая часть (равенства или эквивалентности) в них не является определяемым, а лишь содержит его в качестве своей собственной части.

Явное определение – это наиболее простая и наиболее употребительная форма определений. Наличие явного определения в той или иной теории позволяет исключить (элиминировать) определяемое выражение из языка этой теории, заменяя его во всех случаях, где оно встречается, определяющей частью. Употребление его (определяемого) может быть полезно лишь ради сокращения некоторых контекстов.

 

 

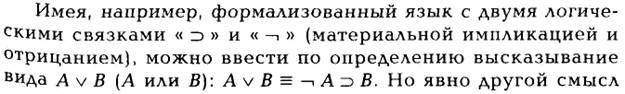
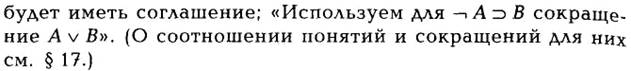
В структурах неявных определений, о которых речь ниже, нельзя выделить определяемое и определяющее в качестве самостоятельных частей, в силу чего они не дают способа элиминации определяемого из тех или иных контекстов.

ВИДЫ ЯВНЫХ ОПРЕДЕЛЕНИЙ

Для определений, посредством которых вводятся понятия (определения имен и предикатов), возможно выделение их видов по характеру видовых отличий этих понятий. Речь идет о характере признаков, по которым выделяется класс предметов или отдельный предмет. Такими признаками могут быть качества, свойства (в частности, свойства реляционного типа) предметов. Таковы, например, определения: «Хорда – это отрезок прямой, соединяющий две какие-нибудь точки окружности»; «Диаметр окружности – это наибольшая хорда окружности»; «Дерево – многолетнее растение, имеющее ствол, крону и корни»; «Жидкость (вещество, находящееся в жидком состоянии) – это вещество, которое имеет собственный объем, но не имеет собственной формы и принимает форму сосуда, в который помещена»; «Прибыль предприятий – это остающийся у предприятия доход после выплаты всех расходов, связанных с производством и реализацией его продукции».

Наряду с такими определениями, которые можно назвать атрибутивными, выделяются генетические и операциональные.

• В операциональном определении видовой характеристикой предметов является указание на некоторую операцию, посредством которой эти предметы могут быть обнаружены и отличены от других предметов.

Например, температуру мы можем определить как состояние предмета или среды, количественная характеристика которого может быть установлена с помощью термометра. В лингвистике операциональный характер имеют определения тех или иных выражений путем указания вопросов, на которые они отвечают, например, «существительное находится в именительном падеже, если (и только если) оно отвечает на какой-нибудь из вопросов «кто?», «что?». К этому же виду будет относиться и определение кислоты, как жидкости, окрашивающей лакмусовую бумажку в красный цвет.

• Весьма важным видом явных определений являются определения через абстракцию.

Заметим, что этот способ применяется для определения имен таких абстрактных объектов (предметно-функциональных характеристик предметов) как: масса, форма, площадь, длина и т.п. Определение здесь осуществляется посредством особого типа отношений, называемых отношениями типа равенства (иногда – эквивалентности). Примерами таких отношений могут служить подобие (фигур), конгруэнтность отрезков: «Форма геометрической фигуры есть то общее, что имеется у всех подобных фигур». Задав отношение равновесомости двух тел, уравновешиваемости их на чашечных весах, можно определить вес как то общее, что является одинаковым у всех равновесомых предметов и различным у неравновесомых.

К приведенному перечню известных видов явных определений следовало бы, как нам представляется, добавить фактически широко применяемый способ определения, который можно было бы назвать лингвистическим. Этот способ применяется для определения некоторых абстрактных объектов и состоит в том, что в качестве характеристик указываются языковые формы их выражений. Таким образом, в предыдущих частях учебника вводились понятия: «свойство», «отношение», «атрибутивное свойство», «реляционное свойство» по виду представляющих их предикатов. Напомним, что отношение, например, есть такая характеристика систем объектов, которую представляют более чем одноместные предикаты А(х₁, ..., х_n), а свойства – одноместные предикаты А(х). По структурам одноместных предикатов мы различаем также атрибутивные и реляционные свойства (см. § 12).

В лингвистике этот способ дефиниции применяется при определении частей предложения и некоторых других понятий.

В заключение обзора видов явных определений отметим одну их особенность. При широком понимании свойства, как характеристики предмета, выраженной одноместным предикатом (см. § 13),– очевидно, что в генетических, операциональных, лингвистических и определениях через абстракцию – во всех этих определениях в качестве видового отличия вводимого понятия указывается некоторое свойство! На этом основании, казалось бы, их можно рассматривать как виды атрибутивных... Однако при характеристике атрибутивных определений мы употребляли термин «свойство» в более узком смысле (см. § 13). Учитывая это, точнее можно было бы сказать, что атрибутивное определение – это явное определение, отличающееся от всех только что перечисленных видов. Иначе говоря, атрибутивные определения – это такие определения, которые не являются лингвистическими, операциональными, генетическими и определениями через абстракцию, то есть все остальные.

Обратим внимание читателя на примечательный факт. Такой способ определения «атрибутивных определений» может, вообще говоря, рассматриваться как частный случай еще одного из видов явного определения – определения посредством отрицания. Этот прием определения чаще всего применяется в случаях, когда удается определить все виды предметов некоторого класса (выделенные по одному и тому же основанию), кроме одного. Тогда предметы этого вида определяются именно как «все остальные» в данном роде. Например: «Формула является выполнимой (в узком смысле), если и только если она не является ни тождественно-ложной, ни тождественно-истинной». Надеемся, что читатель без труда может привести примеры возможных определений этого вида. Принимая во внимание еще один вид явных определений – только что рассмотренный – и возвращаясь к определению атрибутивных дефиниций, мы должны из класса «остальных» исключить, конечно, и определения посредством отрицания.

 

ВИДЫ НЕЯВНЫХ ОПРЕДЕЛЕНИЙ

Вспомним сказанное выше о том, что неявные определения отличаются от явных тем, что в них нельзя выделить в качестве самостоятельных частей определяемое и определяющее выражения и, значит, нельзя представить в виде равенства или эквивалентности, левая часть которых представляла бы определяемое выражение. Однако, как мы уже говорили, есть вид неявных определений – контекстуальные определения,– которые имеют вид равенства или эквивалентности. Тем не менее левая часть этого равенства есть не определяемое, а некоторый контекст, в частности,– возможно предложение, включающее определяемое как некоторую свою правильную часть. Таким – неявным – образом определяются, например, выражения, образуемые посредством определенной и неопределенной дескрипций (?хА(х)), εхА(х) – см. §6), а именно: непосредственно определяются при этом предложения вида В(?хА(х)) и В(εхА(х)). Определения их мы уже имели. Напомним их здесь.

 («Существует предмет х (из области D), который обладает свойством А и В и притом он является единственным, обладающим свойством А».)

 

 

Пример

 

Предложение «То небесное тело, которое является естественным спутником Земли, есть остывшее тело» истинно, если и только если существует небесное тело, которое является естественным спутником Земли и является остывшим, и для любого тела, которое является естественным спутником Земли, верно, что оно совпадает с упомянутым (х)».

Итак, форма определения здесь есть эквивалентность. Однако читатель должен увидеть, что левая ее часть – В(?хА(х)) и В(εхА(х)) – содержит определяемое (соответственно: ?хА(х) и εхА(х)) как свою правильную – не совпадающую с целым – часть. В правой же – определяющей – части это выражение уже не содержится.

Определения такого – неявного – вида всегда можно рассматривать как явное определение всего выражения, стоящего в левой части, в данном случае – предложения. Точнее говоря, оно представляет собой схему определений любых предложений указанной структуры.

Таким образом, одно и то же определение может быть явным относительно одного выражения и неявным контекстуальным относительно термина «необходимо».

В приведенных ранее таблицах, выражающих условия истинности высказываний, образованных посредством операций  мы имеем явные определения соответствующих высказываний и неявные контекстуальные определения указанных операций как функторов. Например, табличное определение высказывания «р & q» в развернутой форме может быть представлено так: высказывание вида р & q эквивалентно (по определению) такому высказыванию, которое имеет истинностные значения, указанные в таблице (см. § 10). Но здесь же мы имеем неявное (контекстуальное определение самого функтора «&», как операции, посредством которой образуются высказывания рассматриваемого вида).

В традиционных учебниках по логике контекстуальным определением некоторого термина называют обычно разъяснение его смысла и предметного значения посредством указания совокупности предложений или высказываний, содержащих этот термин. Такими совокупностями, по мнению многих авторов, могут быть совокупности аксиом некоторой математической теории, совокупность уравнений и т.п. Более того, имеется мнение, что всякая совокупность слов, всякий контекст, в котором встречается интересующее нас выражение, является неявным его определением.

Однако это, очевидно, не так. Определяет ли смысл (и соответственно предметное значение) слова «дядя» следующий известный пушкинский контекст?

 

Мой дядя самых честных правил,

Когда не в шутку занемог,

Он уважать себя заставил

И лучше выдумать не мог.

 

В современной логике выяснено, что далеко не всякая совокупность предложений, в которых содержится некоторый термин, является его неявным определением. Установлен точный критерий, в каких случаях имеет место неявная определимость, например, некоторого предикатора Р множеством содержащих его предложений I(Смирнов В.А. Логические методы анализа научного знания.– М., 1987.– Гл. 2, 3.).

Используя этот критерий, можно, конечно, говорить, что в соответствующих – положительных – случаях мы имеем неявное определение термина. Однако речь здесь идет об определении не как об особой логической операции, а как о некоторой характеристике контекста, его отношении к термину.

Другим важным видом неявных определений являются индуктивные определения («определения по индукции»). С определением этого вида мы уже имели дело при определении формул ЯЛВ и ЯЛП, термов в ЯЛП (см. § 10 и § 11). Эта форма неявного определения применяется для определения общих имен и является таким образом специфическим способом введения понятий в науку. Она применяется в тех случаях, когда класс-объем определяющего понятия может быть разделен на две части: 1) совокупность некоторых элементарных объектов этого класса и 2) совокупность объектов, которые могут быть построены из других объектов этого же класса, а в конечном счете – из элементарных, посредством некоторых операций.

Рекомендуем читателю обратиться к упомянутым только что определениям и проанализировать их с точки зрения данного здесь их описания. Дополнительно к этим определениям укажем известное определение термина «натуральное число».

Элементарным объектом класса натуральных чисел является 0 (ноль). А операцией, посредством которой любое натуральное число (кроме 0) может быть образовано из другого, и в конечном счете из 0, является прибавление единицы, или, как иначе говорят еще, операция образования объема, «следующего за n» (для обозначения объекта, «следующего за л» принято обозначение «n¹»). Все определение термина «натуральное число» выглядит так.

1. 0 есть натуральное число.

2. Если n – натуральное число, то n' (следующее за n) – натуральное число.

3. Ничто другое, кроме указанного в пунктах 1 и 2, не есть натуральное число.

Следует обратить внимание на специфику индуктивных определений, состоящую в том, что определяемое выражение используется здесь в определяющей части (см. определение формулы, терма – § 11). Это создает видимость известной ошибки в определениях «порочного круга», но «круг» фактически «разрывается» благодаря именно расслоению класса предметов на некоторые уровни (известно, что до открытия логикой индуктивных определений в науке возникали в определенных случаях трудности, связанные как раз с неумением выйти из кажущегося «порочного круга», по видимости, неизбежно возникающего в некоторых случаях).

Среди неявных определений также можно выделить виды генетических и операциональных. Так, индуктивное определение, по существу, является генетическим, поскольку основная его часть состоит в указании способа построения объектов из других и в конечном счете – из элементарных. Таким образом, есть виды явных операциональных и генетических, а также и неявных определений этого типа.

Известен, кроме рассмотренных выше, еще один вид неявных определений – рекурсивные определения. В этих определениях задаются операции вычисления значений предметных функторов, то есть вычисление возможных значений форм имен вида: «х + y», «х • у» и т. д. Широкое применение этот вид определения находит в математике и математической логике.

В заключение данного параграфа обращаем внимание читателя на то, что в учебниках традиционной логики среди явных определений в качестве особого вида выделяют обычно так называемые определения «через род и видовое отличие». При этом имеется в виду, что в определяющей части этих определений указывается некоторый класс предметов («род») и видовое отличие, посредством которого в этом классе выделяется определяемый класс предметов. Например, «Ромб есть плоский, замкнутый четырехугольник (род), все стороны которого равны (видовое отличие)».

Однако мы видели уже, что всякое понятие представляет собой результат обобщения предметов некоторого класса и мысленного выделения его в пределах более широкого класса. То есть понятие всегда имеет родовидовую структуру. Таким образом, определение «через род и видовое отличие» – это просто определение общего или единичного имени, посредством которого вводится некоторое понятие. Это значит, что, в частности, индуктивное определение есть тоже определение через род и видовое отличие. Более того, указание рода необходимо во многих других видах определений. Например, при определении выражения типа А(х) (одноместного предиката) необходимо указание области значений х. Аналогично дело обстоит и при определении предметных функторов. Следовательно, определение «через род и видовое отличие» не является особым видом определения.

 Правила и возможные ошибки в определении

Правила определения – это необходимое условие логической правильности такой операции. Есть ряд правил, существенных для определения выражений в формализованных языках. Они связаны с употреблением переменных в этих языках. Основное из них – ни в какой из частей (ни в определяемой, ни в определяющем выражении) определений не должно быть свободных переменных, отсутствующих в другой части. Предикат «х дядя у» определяется как: существует г такой, что х есть брат z, а у есть сын или дочь z, где область значений х, у, z – люди. Используя в естественном языке вместо переменных их аналоги – общие имена, в данном случае одно – человек, при этом с числовыми индексами для различения различных предметов, получили бы определение: «человек₁ есть дядя человека₂ если и только если – по определению – существует человек₃ такой, что человек₁ есть брат человека₃, а человек₂ – сын или дочь человека₃. Но определение было бы неправильным, если бы в определяющей части переменная «z» или соответственно «человек₃» была взята без квантора «существует», то есть в качестве свободной переменной. Ошибки такого рода приводят к возможности возникновения противоречий.

Однако для определений в естественном языке, которые здесь в основном имеются в виду, более существенны правила, сформулированные в традиционной логике. Несмотря на кажущуюся тривиальность этих правил, ошибки, связанные с их нарушениями, являются весьма распространенными. К этим правилам относятся:

1. Определение должно быть ясным. Это звучит банально. Поскольку определение приписывает смысл определяющему, он должен быть доступен по крайней мере пониманию. Вместе с тем само это требование нуждается в разъяснениях. Ясность определяющей части зависит, конечно, от выполнения синтаксических и семантических требований к построению выражения. Но главное, должны быть известными предметные значения входящих в его состав терминов. Последние в свою очередь тоже могут быть определены посредством терминов, значения которых известны, однако этот процесс нельзя продолжать бесконечно. В составе теорий некоторое множество (по возможности минимальное) терминов принимается за исходное в качестве основы для определения всех других, употребляемых в этой теории. Предметные значения неопределяемых терминов разъясняются посредством тех или иных приемов, сходных с определением (см. далее,– приемы, сходные с определением).

При анализе того или иного отдельно взятого определения невозможно иногда решить вопрос, известны ли предметные значения употребленных в нем терминов. Это значит, что о ясности или неясности определения с указанной точки зрения надо решать с учетом ситуации, в которой дано определение, аудитории, для которой оно предназначено. Например, философское направление, называемое неокантианством, определяют как позднюю школу трансцендентального идеализма. Читателю, незнакомому с философией, не ясно, что такое сам «трансцендентальный идеализм». Но тем, кому предназначено определение, возможно, это и ясно, тем более данное определение корректно, если оно сочетается с разъяснением того, что такое трансцендентальный идеализм.

К условиям ясности определения надо отнести также требование указывать в определяющей части лишь то, что, необходимо и достаточно для выделения тех предметов или связей, которые должны составить предметное значение определяемого термина. Почти все философы, касающиеся понятия закона (природы), определяют его как необходимую, всеобщую, устойчивую, повторяющуюся связь.

Между тем ясно, что если связь является необходимой, то она устойчива и всеобща, и значит, повторяема – одним словом, определение загромождается здесь включением наряду с основными признаками понятия также и производных. Выявление последних – это уже процесс развития введенного понятия.

Читатель может, очевидно, сам решить вопрос, насколько ясными являются следующие определения части речи (взятые из энциклопедических изданий): «Части речи – грамматические категории, по которым распределяются слова данного языка. В основе каждой части речи лежит понятие, получающее в данном языке единообразное грамматическое выражение в количественно неограниченном ряде слов различного вещественного значения и в связи с этим выступающее в них в качестве их грамматического значения».

Конечно, нуждается в разъяснении здесь указание на некоторое понятие, которое «... лежит...» в основе каждой части речи и то, что представляет собой «... единообразное... выражение...» в бесконечной последовательности слов.

Еще пример. «Сущность – это внутреннее содержание предмета, выражающееся в единстве всех многообразных и противоречивых форм его бытия».

Едва ли ясно, даже искушенным в философии людям, что такое «содержание предмета» и тем более «внутреннее» содержание его и в чем же состоит «единство всех многообразных и противоречивых форм его бытия».

Для обеспечения ясности определения термина весьма важно указание рода, к которому принадлежат соответствующие предметы.

В определениях философских терминов мы постоянно встречаемся с оборотами: «качество есть философская категория...», «количество есть философская категория...» и т.п.

Это было бы правильно, если бы определяемыми были «качество», «количество» и т.п. (в кавычках), то есть имена самих определяемых выражений и понятия, с которыми связываются эти выражения в философии, но сами качество, количество, материя и т.п.– суть определенные характеристики предметов и явления действительности, а не понятия философии.

Ошибка этого же типа (неправильное указание рода) встречается при определении таких элементов частей речи, как «глагол», «существительное», «прилагательное» и др. Обычно эти определения звучат так: «Существительное есть часть речи...»; «Глагол есть часть речи...» и т.п. Вместе с тем части речи определяются как «классы, разряды, множества в том или ином отношении однородных слов». В силу взаимозаменимости определяемого и определяющего получается тогда, что «существительное есть класс, разряд, множество слов...». Наряду с этим говорят также, что «существительное изменяется по падежам», «глагол спрягается» и т. п. Однако очевидно, что «склоняются», «спрягаются» не классы слов, а отдельные слова... Существительное – как и глагол, и прилагательное – есть не «класс слов», а слово (слово, обозначающее тот или иной предмет или, иначе, отвечающее на вопрос: кто? что?).

Другая ошибка, связанная с родом вводимых по определению понятий, состоит в том, что он вообще не указывается. Учащиеся, например, нередко его просто «проглатывают», формулируя определения по схеме: «Храбрость – это когда...», «Мужество – это когда...».

2. В определении не должно быть круга. Это значит, что термин, встречающийся в определяющей части, не должен определяться через определяемый термин. В традиционной логике, например, правильное мышление определялось нередко как такое, которое подчинено законам логики, а законы логики как такие законы, которые обусловливают логическую правильность мышления. Здесь типичный «круг» в определении. Частным случаем этой ошибки является попытка определить некоторый термин через самого себя (хотя возможно, и в сочетании с другими терминами). Например, «корень» (слова) – эта главная значимая часть слова, в которой заключено общее значение всех однокоренных слов».

Едва ли здесь можно уяснить смысл определяющей части, не зная, что такое корень.

Можно усмотреть наличие круга в определении веса как того общего, что есть у всех равновесомых тел (см. определение через абстракцию). Однако круга нет, поскольку равновесомость определяется как уравновешенность тел на скалочных весах, то есть без использования понятия веса.

Определение туриста как человека, занимающегося туризмом, также неправильно квалифицировать как тавтологичное, если разъяснено независимо от термина «турист», что означает туризм как деятельность.

3. Определение должно быть соразмерным. Это правило относится лишь к реальным определениям и, по существу, лишь к определениям общих имен. Это требование означает, что определяющая часть должна выделять именно тот класс предметов, который представляет определяемая. Различают три рода ошибок, связанных с нарушением правила:

1) определяющая часть представляет лишь подкласс того класса, который имеется в виду при определении. В этом случае говорят, что определение является «слишком узким». Например, слишком узким можно считать определение арифметической прогрессии как конечной последовательности чисел, каждое из которых получается из предыдущего прибавлением к нему одного и того же числа (называемого разностью прогрессии). В известном понятии прогрессии мы отвлекаемся от того, является представляющий ее ряд конечным или бесконечным;

2) класс, который представляет определяющая часть, то есть объем понятия, которое приписывается в качестве смысла определяемому термину, шире того класса, который имеется в виду под определяемым термином (определение является «слишком широким»). Слишком широким было бы определение окружности как замкнутой линии, все точки которой отстоят на равном расстоянии от некоторой точки, называемой центром окружности. Для того чтобы определение было в данном случае соразмерным, нужно вместо «замкнутой фигуры» сказать «плоская замкнутая фигура»;

3) бывают случаи, когда определение является в некотором отношении слишком широким, а в другом – слишком узким; таким, что в класс предметов, выделяемый в определяющей части, попадают не все предметы, которые должны в нем быть, а предметы, которые не относятся к нему. Пример: «Литературное произведение – это письменное или печатное изложение какой-либо истории». Ясно, что объем указанного здесь понятия охватывает далеко не все литературные произведения. С другой стороны, едва ли относится к литературным произведениям, например, протокол какого-либо допроса или жалобы, которые могут быть элементами этого объема.

Очевидно, что несоразмерность определения в рассмотренных случаях проявляется в том, что эти определения не согласуются с некоторыми утверждениями, уже принятыми в той области знания, к которой относится определяемый термин. Например, определение ромба как прямоугольного четырехугольника, будучи в одном отношении слишком узким, в другом – слишком широким, не согласуется (противоречит) соответственно с утверждениями геометрии о том, что не всякий ромб прямоуголен и не все прямоугольники являются ромбами. Этому требованию не удовлетворяет и известное определение качества как «существенной определенности» предмета, неотделимой от его бытия». Оно не согласуется с не менее известным утверждением философии о существовании качественных изменений предметов. В самом деле, согласно этому определению, каждое качественное изменение предмета надо было бы считать просто переходом от одного предмета к другому, как устранение бытия одного предмета с появлением другого.

С учетом этого напрашивается обобщение правила соразмерности: определение должно согласовываться с истинными (принятыми) утверждениями той области знания, к которой относится определяемое.

Однако возможны случаи, когда о несоразмерности определений можно судить не в зависимости от наличия специальных знаний, а лишь на основе чтения синтаксических или семантических правил употребления терминов соответствующего языка. Определяя, например, неокантианство как «одно из направлений трансцендентальной философии», мы получили бы слишком широкое определение. Это очевидно из семантики (смысла) словосочетания «одно из...». Ясно, что «одно из...» указывает на любое из множества направлений трансцендентальной философии и тем самым не является видовым отличием неокантианства. Таким образом, указанную ошибку в этом определении может усмотреть и тот, кто не знает, что такое трансцендентальная философия (и кому, в силу этого, определение кажется неясным).

В заключение – нечто из области анекдотов – пример вообще надуманного определения, содержащего почти все возможные ошибки.

Когда известный естествоиспытатель Кювье зашел в Академию наук в Париже, где работала комиссия по составлению энциклопедического словаря, его попросили оценить определение слова «рак», которое было только что «удачно» найдено. «Мы нашли определение понятию «рак»,– сказали члены комиссии,– вот оно: «Рак – небольшая красная рыба, которая ходит задом наперед».– «Великолепно,– сказал Кювье.– Однако разрешите мне сделать небольшое замечание. Дело в том, что рак не рыба, он не красный и не ходит задом наперед. За исключением всего этого, ваше определение превосходно».

Приемы, сходные с определением

Поскольку определение используемых в том или ином рассуждении терминов, выражений является важным условием точности нашего мышления, то возникает вопрос: не следует ли определять все употребляемые нами слова и выражения? На это надо ответить так: все употребляемые в языке выражения определить невозможно. Мы можем определить одно через другое, другое через третье – но эта последовательность не может продолжаться без конца! Что-то должно приниматься без определений. Когда рассматривалось понятие знака, отмечалось, что некоторые знаки естественных языков стихийно приобретают предметные значения в процессе формирования и использования языка как средства общения. Их связь с предметами осуществляется не логическим способом, то есть посредством приписывания им смысла (не определением). В конечном счете, именно такие языки являются исходными для определений, то есть сами не определяются. Но не имея возможности определить все употребляемые выражения, к определениям надо стремиться, но крайней мере, всегда, когда необходима точность в решении тех или иных вопросов. Они составляют необходимый элемент доказательства тех или иных утверждений. Например, при доказательстве любой теоремы мы должны точным образом очертить класс предметов, к которым она относится. Это можно сделать, лишь определив общее имя, обозначающее предметы этого класса. Точно определен должен быть смысл и того, что утверждается в теореме. Как можно, например, доказать, что диагонали ромба всегда перпендикулярны, не определив, что называется ромбом и что означает перпендикулярность диагоналей? Мы не можем понять правил грамматики и точно применять их, если не являются достаточно ясными встречающиеся в их формулировках выражения. Особая точность требуется в формулировках правовых норм, юридических законов. Нельзя обвинить человека в совершении того или иного проступка или преступления и тем более доказать его виновность, не имея определений соответствующих видов правонарушений.

Вместе с тем надо иметь в виду, что процесс выработки определения, или, что то же, формирования понятия, которое предполагается ввести определением, представляет собой нередко очень сложный процесс. В силу этого, даже при наличии сознания необходимости определения, во многих науках, особенно в тех, которые имеют дело со сложными, конкретными явлениями действительности, даже существенные термины языка не имеют точных смыслов, а вместе с этим и точных предметных значений.

Когда по каким-либо причинам мы не можем указать предметное значение какого-либо термина посредством приписывания этому термину смысла, важно сделать это хотя бы с какой-то степенью точности каким-либо другим образом. Одним из таких приемов является указание (называемое также остенсивным определением). Буквально он состоит именно в указании по крайней мере некоторых экземпляров класса подразумеваемых предметов или самого предмета, если речь идет об единственном предмете. Детей знакомят, например, с разными цветами, показывая их на специальной шкале цветов. Сюда же относятся и словесно (вербально) формулируемые примеры интересующих нас предметов или явлений. Вообще, применение приема указания основано на наличии у людей некоторой природной интуитивной способности угадывать в отдельных предметах класса нечто общее, что объединяет эти предметы в класс. Ребенок достаточно хорошо усваивает употребление слов «собака», «кошка», «корова», «лошадь» и др. на основе знакомства с отдельными экземплярами соответствующих животных. Однако, если попытаться разъяснить, кто такие пресмыкающиеся, указывая в качестве примеров на змей, ящериц, жаб, то едва ли человек догадается, исходя из этих примеров, что к пресмыкающимся относится, например, и крокодил. Дело, очевидно, в том, что класс пресмыкающихся более разнороден, нежели класс домашних животных. Поэтому применение приема указания в этом случае значительно менее эффективно. И тем более этот способ выяснения значений терминов не применим, когда речь идет об объектах вообще недоступных наблюдению: электрон, протон, электромагнитные волны, вечный двигатель, скорость света и т.д.

Другой прием, сходный с определением – описание. Применяется в случаях, когда речь идет о наглядно представимых предметах или явлениях и состоит в перечислении в основном некоторых внешних признаков предметов, по которым могли бы составить представление о них, хотя среди перечисленных признаков могут быть и существенные (чувственно невоспринимаемые). Например: тигр – это млекопитающее семейства кошачьих, один из наиболее крупных современных хищных зверей (длина тела до 3 м, вес до 320 кг). Голова круглая, с короткими ушами. Бока красновато-рыжей окраски с черными поперечными полосами и т.д.

Близким к описанию является прием, который называется характеристикой. В отличие от описания решение задачи уточнения значения термина осуществляется здесь не путем формирования наглядного образа, а посредством перечисления наиболее типичных (характерных), более или менее существенных для предметов данного класса черт. Например, перечисление основных симптомов той или иной болезни или характеристика нефти как жидкости темного цвета, горючей, маслянистой, имеющей специфический запах, встречающейся в недрах земли.

Характеристика более близка к понятию, но отличается отсутствием свойственной понятиям упорядоченности признаков. В силу этого характеристика не гарантирует однозначного выделения соответствующего класса объектов. Иначе говоря, термин получает при этом некоторое смысловое содержание, но его смысл не определяется в «строгом смысле» этого слова (см. § 6)

Перечисление признаков в характеристике не связывают обычно с требованием: «Каждый из признаков необходим, а все вместе достаточны для выделения рассматриваемых предметов». Так, перечисленные выше черты, характеризующие нефть, не могут служить точным критерием того, что в том или ином случае мы имеем дело с этой жидкостью.

В качестве элемента характеристик предметов нередко применяется прием метафорических сравнений, в основе которых лежат некоторые аналогии предметов. Так, подчеркивая значение нефти в народном хозяйстве, называют ее «черным золотом», архитектуру характеризуют как «застывшую музыку», верблюда – как «корабль пустыни».

«Определения» такого рода сами по себе могут служить примерами характеристик.

К числу характеристик могут быть отнесены также и некоторые определения, страдающие, например, ошибками несоразмерности. Так, приведенное выше определение неокантианства как одного из направлений трансцендентальной философии не годится как определение, но вполне может быть принято как одна из возможных характеристик неокантианской философии.

В некоторых случаях прием сравнения применяется и в качестве самостоятельного способа разъяснения того, что имеется в виду под тем или иным термином.

Он состоит в указании чего-то существенно общего у предметов, которые имеются в виду, с другими предметами и вместе с тем того, что их отличает от этих других. Упрямство, можем мы, например, сказать, подобно настойчивости, упорству. Но отличается от них тем, что представляет собой вид слабости человека, в то время как упорство и настойчивость – проявление силы его характера.

Наконец, характеристика, как один из приемов, сходных с определением, часто состоит в том, что вместо формулировки общего понятия некоторого класса указывают, по крайней мере, некоторые основные виды предметов этого класса. Не имея возможности, например, дать определение игры вообще, мы можем указать, что имеют в виду под термином «игра»: во-первых, игра как имитация какой-нибудь деятельности (детские игры в войну, дочки-матери и т.д.) во-вторых, игра как состязание на ловкость, сообразительность, выносливость (спортивные игры); и, наконец, в-третьих, игра как деятельность, в которой – главная цель – денежный или материальный выигрыш (азартные игры).

В заключение главы отметим следующее. Приемы, сходные с определением, зачастую используются не только в качестве самостоятельных приемов познания. Их применение довольно часто предпосылается определениям, что представляет собой важный педагогический прием, во многом облегчающий понимание и усвоение определений. Важно заметить и то, что те, кому предназначено определение, должны стараться по возможности зрительно представить себе те объекты и ситуации, которые вводятся определением, то есть пытаться связать их с какими-то образами. Известно, что какие-то зрительные конструкции можно сформировать даже тогда, когда речь идет об абстрактных, ненаблюдаемых объектах. Таким образом определения становятся более «осязаемыми», запоминающимися, и во всяком случае это облегчает использование определений.

 

Упражнения

 

1. Дайте характеристику следующих определений: укажите, что является определяющим и определяемым, к каким видам (по рассмотренным выше основаниям) они относятся:

а) Дипломатия есть мировая, оперативная работа по осуществлению внешней политики государства;

б) Шар есть геометрическое тело, которое образуется вращением полукруга вокруг диаметра;

в) Утверждение, что всякое тело имеет какой-то удельный вес, означает, что всякое тело испытывает определенную силу притяжения к Земле, приходящуюся на каждый кубический сантиметр его объема;

г) Форма фигуры – это то общее, что есть у всех подобных и только подобных фигур;

д) Предмет мысли – это то, что представлено в языке единичным или общим именем;

е) Реляционное свойство (некоторого предмета) – это такая характеристика предмета, которая выражена в виде одноместного предиката, образованного из некоторого многоместного предиката, то есть образованного из предиката, содержащего более чем одну свободную переменную;

ж) Прямой угол – это угол, который не является острым и тупым;

з) Понятие многоугольника:

1) Треугольник есть многоугольник.

2) Если некоторая фигура – многоугольник, то фигура, которая получается в результате построения на какой-то из ее сторон треугольника – с вычеркиванием этой стороны,– является многоугольником.

3) Ничто, кроме указанного в пунктах 1) и 2), не является многоугольником;

и) Укажите, можно ли определение пункта в) рассматривать как определение выражения «удельный вес некоторого тела» и если да, то к какому виду оно относится?

2. Дайте анализ (с точки зрения логической правильности) следующих определений:

а) Хлопок – это белое золото;

б) Гималаи – высочайшие горы мира;

в) Кислород – необходимое условие жизни;

г) Антонимы – слова противоположного значения;

д) Понятие – это мысль о предмете;

е) Учитель – человек, который учит кого-нибудь;

ж) Виктимология – быстро развивающаяся в настоящее время отрасль криминологии;

з) Олигоцен – третья эпоха палеогена;

и) Один процент от какого-то целого – это одна сотая часть этого целого;

к) Угол есть фигура, образующаяся при вращении луча вокруг своей начальной точки (из учебника математики). Укажите фигуру соответствующую 90°, 180°, 360°. Можете ли Вы указать фигуру, соответствующую углу в 3600°?

л) Равнобедренный треугольник – это треугольник, не являющийся равносторонним и разносторонним треугольником.

3. Попытайтесь дать определение выражениям: «мужество», «самолет», «буква», «кульминация», «педагог», «талантливый педагог».

 

СУЖДЕНИЕ (ВЫСКАЗЫВАНИЕ) КАК ФОРМА МЫШЛЕНИЯ

§ 28. Общая характеристика и роль суждения в познании

Наряду с понятием к числу основных форм мышления относится суждение. Его определяют обычно как утверждение или отрицание чего-либо о чем-либо, хотя это определение относится лишь к особому виду суждений, а именно – к простым суждениям. Мысль этого типа, вообще говоря (пока без различения простых и сложных суждений, о которых речь пойдет ниже) представляет собой описание некоторой ситуации в той или иной познаваемой области действительности и утверждение или отрицание наличия этой ситуации в данной области. Эта форма мышления является, по существу, обязательным элементом всякого познания, в особенности связанного с процессами рассуждения, с осуществлением выводов и построением доказательств. В этой форме фиксируются результаты познания отдельных предметов, классов предметов, некоторых ситуаций вообще. Например, «Каждая планета Солнечной системы вращается вокруг своей оси». Можно сказать, что в этом суждении утверждается наличие в действительности ситуации: вращение вокруг своей оси каждой планеты Солнечной системы. В суждении «Для всякого проводника верно, что если по проводнику проходит ток, то он нагревается»,– утверждается наличие – для каждого проводника – связи между прохождением тока по нему и его нагреванием. В суждении же «Ни одна планета Солнечной системы не является неподвижной» отрицается наличие в действительности ситуации покоя (отсутствия движения) каждой планеты Солнечной системы.

В силу того, что в суждении утверждается или отрицается наличие какой-то ситуации действительности, оно – при условии точной и правильной формулировки – является истинным или ложным.

Всякая мысль, как мы уже знаем, выражается в некоторой знаковой – обычно языковой – форме. Для суждения таковой является повествовательное предложение. Само суждение составляет всегда смысл некоторого повествовательного предложения. Суждение, рассматриваемое вместе с его знаковой формой, как мы уже говорили раньше, называют высказыванием. Поэтому характеристики «истинно» или «ложно» относятся зачастую не к самому суждению, а к высказыванию, а иногда и к самому повествовательному предложению, являющемуся законом некоторого суждения (Здесь, как это обычно принято, мы рассматриваем суждение как некоторый результат познания, хотя его можно рассматривать – наряду с понятием – и как определенную форму мыслительной деятельности, как способ языковой обработки чувственных данных, как специфический прием выделения и фиксации интересующих нас ситуаций действительности.).

• Таким образом, более подробно суждение можно охарактеризовать как мысль, выражаемую в знаковой форме повествовательного предложения, содержащую описание некоторой ситуации и утверждение или отрицание наличия этой ситуации в рассматриваемой области действительности.

С наличием в суждении некоторого утверждения или отрицания неразрывно связано свойство суждения быть истинным или ложным. Впрочем, отрицание наличия некоторой ситуации всегда можно истолковать (и обычно так и делается в современной логике) как утверждение наличия отрицательной ситуации, которая состоит как раз в том, что нечто отсутствует в действительности. Говоря о том, что труд есть источник всех благ человеческого общества, мы утверждаем наличие именно такого положения дел в действительности, согласно которому все блага общества являются результатами труда людей.

В высказывании же «Без труда невозможно достичь серьезных успехов» утверждается отсутствие такой ситуации, когда некоторые успехи не связаны с затратой труда.

Ситуация – связь между наличием тока и проводника и наличием вокруг него электромагнитного поля – может быть выражена в суждении: «Для всякого проводника верно, что если по нему проходит ток, то вокруг него существует электромагнитное поле».

Поэтому всегда возможно считать, что суждение есть некоторое утверждение, а именно – утверждение о наличии некоторой положительной или отрицательной ситуации в действительности.

Эта возможность связана с применением общей схемы определения понятия истинности некоторого высказывания А (схема Тарского) «Истинно «А», если и только если А», где «А» – имя данного высказывания А, а А в правой части есть знак утверждаемой в данном суждении ситуации. (Вся схема должна быть прочитана так: «высказывание «А» истинно, если и только если ситуация А имеет место в действительности».)

 

 

Именно наличие утверждения или отрицания описываемой ситуации отличает суждение от понятия. В понятии мы просто описываем некоторую ситуацию с целью мысленного ее выделения. Выделив ситуацию, мы можем высказать о ней то или иное суждение.

Аналогично тому, как один и тот же класс предметов может быть выделен в различных понятиях, обобщающих предметы класса по разным признакам, одна и та же ситуация может быть по-разному выделена и описана в различных суждениях. Ситуация, выраженная в суждении: «Для всего проводника верно, что если по нему проходит ток, то вокруг него существует электромагнитное поле», может быть выражено в другом суждении: «Для всякого проводника верно, что если вокруг него не существует электромагнитное поле, то по нему не проходит электрический ток». Разные понятия, в которых обобщаются одни и те же предметы одного и того же класса, мы называли, как помнит читатель, равнозначным. Различные суждения, в которых описывается объективно одна и та же ситуация, можно называть содержательно эквивалентными (иногда также равносильными или равнозначными). (Просто «эквивалентными» или «равнозначными» называют высказывания с одинаковыми истинностными значениями; при этом не обязательно связанные между собой по содержанию.)

Поскольку понятие в отличие от суждения содержит только описание некоторого предмета и ситуации без утверждения наличия или отсутствия ее в действительности,– оно не является ни истинным, ни ложным. Конечно, при условии, что имеется в виду понятие само по себе, что мы обычно и имеем в виду при рассмотрении понятия, а не понятие о чем-либо. Понятие того или иного человека о чем-либо всегда истинно или ложно, но именно потому, что выражается в форме суждения. Свое понятие о ромбе я могу выразить так: «Ромб есть плоская, замкнутая, четырехугольная фигура с равными сторонами». В таком случае мое понятие о ромбе, очевидно, истинно. Понятие же ромба само по себе – плоская, замкнутая, четырехугольная фигура с равными сторонами – конечно, не истинно и не ложно. Сравним: «Поражение Парижской коммуны» и «Парижская коммуна потерпела поражение»; «Все жидкости упруги» и «Упругость всех жидкостей».

В современной логике вместо термина «суждение» предпочитают употреблять термин «высказывание». Однако термином «суждение» в традиционной логике обозначали именно некоторый смысл повествовательного предложения с учетом того, что он может быть общим для различных знаковых форм. Иначе говоря, учитывалось, что одно и то же суждение может быть выражено в различных формах повествовательных предложений в пределах даже одного языка, а тем более в различных языках. Можно, например, утверждать, что «Всякий человек способен мыслить» и что «Все люди обладают способностью мышления», но в обоих случаях выражается одна и та же мысль (одно и то же суждение). Заметим, однако, что предложение «Не найдется человека, который не может мыслить» представляет собой, хотя и содержательно эквивалентное предыдущим, но, как увидим из дальнейших определений, другое суждение.

Напомним, что в описанном выше языке логики предикатов суждения выражают интерпретированные формулы, не содержащие свободных переменных (см. § 11).

Таким образом, говоря о суждении, мы хотя и должны отдавать себе отчет, что оно представлено в некоторой знаковой форме, но не обязательно иметь в виду какую-либо определенную знаковую форму. Говоря же о высказывании, имеем в виду определенную знаковую форму вместе с ее смыслом. Когда же имеем в виду лишь саму знаковую форму высказывания,– отвлекаясь от ее смысла, то есть выражаемого в ней суждения,– то употребляем «повествовательное предложение».

Знание видов – логических структур – суждений, отношений между суждениями и умение разбираться в возможных преобразованиях высказываний является существенным моментом логической культуры, необходимым условием правильного понимания и выражения мысли, а также корректности логических операций с высказываниями.

Простые и сложные суждения. Виды простых суждений

При выделении видов суждений прежде всего возникает необходимость различать простые и сложные суждения. Простое суждение есть утверждение о наличии или отсутствии каких-либо характеристик у какого-нибудь отдельного предмета, у части или у всех предметов некоторого класса. Например, «Математика – абстрактная наука», «Математика не является легкой наукой», «Всякая наука требует труда для ее усвоения», «Некоторые отрасли знания не являются эмпирическими», «Земля имеет массу, превышающую массу Луны».

Сложным является такое суждение, которое содержит в качестве своей правильной части, то есть части, не совпадающей с целым, некоторое другое суждение. Примерами сложных суждений в языке логики предикатов (как и в ЯЛВ) являются суждения видов  где А и В, в свою очередь, есть некоторые суждения (подформулы соответствующей формулы). Так,  является сложным суждением, поскольку его правильная часть  есть, в свою очередь, суждение, в данном случае – простое (при условии, конечно, что в языке имеется интерпретация логических констант, указана область D возможных значений переменной хи интерпретированным является предикатор Р).

Однако в естественном языке не всегда возможно выделить простые суждения как некоторые составные части структуры сложного высказывания, поскольку не всегда ясна знаковая структура сложного высказывания. Ясно, например, что высказывание «Сегодня идет дождь и неверно, что светит Солнце» являются сложным, ясны также и имеющиеся в его составе простые суждения – «Сегодня идет дождь» и «Сегодня светит Солнце». Но как решить вопрос, является ли простым или сложным высказывание «Нейтрон, как и протон, имеет массу, но в отличие от него лишен заряда»? Его нельзя решить формально – лишь на основе анализа знаковой формы. И вместе с тем по смыслу очевидно, что оно является сложным. В нем легко выделить отдельные суждения: «Нейтрон имеет массу», «Протон имеет массу», «Протон имеет заряд», «Нейтрон не имеет заряда», «Нейтрон отличается от протона тем, что не имеет заряда». Суждение «Только некоторые люди способны любить без надежды на взаимность» также содержит в качестве смысловых составляющих утверждения: «Некоторые люди способны любить без надежды на взаимность» и «Некоторые люди не способны на это».

Очевидно, что в таких случаях, выделение простых суждений является результатом расчленения общего смысла исходного суждения. А это – в свою очередь – значит, что под правильной частью, упоминаемой в определении сложного суждения, надо иметь в виду не обязательно знаковую его часть, но, возможно, и смысловую. Очевидно также и то, что смысловой анализ сложных высказываний естественного языка имеет важное значение как для понимания их смысла (характера содержащейся в ней информации), так и для решения вопросов об их истинности или ложности. Переводя данные высказывания на язык логики предикатов или на машинный язык для введения их в память компьютера, можно представить их в виде конъюнкции указанных простых их частей. Ясно, что они истинны лишь при истинности всех их составляющих.

СТРУКТУРЫ (ВИДЫ) ПРОСТЫХ СУЖДЕНИЙ

Основными частями простого суждения являются: один или несколько субъектов суждения (логических подлежащих) – термины, возможно выражающие понятия и представляющие предметы, о которых нечто в высказывании утверждается или отрицается. Во-вторых, предикат суждения (логическое сказуемое) – часть суждения, выражающая то, что утверждается (или отрицается) о предметах, которые представляют субъекты. В суждении «Солнце есть раскаленное небесное тело» субъект – «Солнце», предикат – «раскаленное небесное тело». В суждении «Земля вращается вокруг Солнца» два субъекта – «Земля» и «Солнце». Из данных примеров видно, что субъект представляет в суждении именно то, что мы хотим охарактеризовать в этом суждении, а предикат сужения – саму характеристику. Таким образом, найти субъект суждения – это ответить на вопрос «Что (или кого) хотят охарактеризовать в суждении?» Соответственно для нахождения предиката суждения надо ответить на вопрос «Как, каким образом хотят охарактеризовать предметы, которые представляет субъект или субъекты?»

В зависимости от содержания предиката суждения, то есть от того, что именно утверждается (или отрицается) о тех или иных предметах, мы различаем суждения, в которых утверждается (или отрицается) наличие некоторого свойства у предмета, в других – существование предмета, в-третьих – отношение между некоторыми предметами. Суждения первого типа называются атрибутивными, вторые – экзистенциальными (суждениями существования), третьи – суждениями об отношениях. Примеры атрибутивного и суждений об отношении даны выше (о Солнце). К числу экзистенциальных относится, например: «Пегаса (крылатого коня, описанного в древнегреческой мифологии) не существует в действительности».

Существование как предикат – это существование в реальной действительности, его надо отличать от существования предмета в некоторой области – универсуме рассуждения. Существование этого типа выражается в ЯЛП квантором существования (3) или соответствующими кванторными словами естественного языка (многие, найдется, некоторые, существует и т.п.). Пегас существует в области объектов древнегреческой мифологии, и мы могли бы сказать, что в числе объектов, в данном случае существ, которые описывались в древнегреческой мифологии, существует крылатый конь, который пробил копытом скалу и дал выход источнику вдохновения поэтов. Мы замечали уже, что каждое суждение можно рассматривать как утверждение или отрицание наличия в действительности некоторой ситуации. Представляя содержание суждения таким образом, мы трактуем его как экзистенциальное.

В атрибутивных суждениях, как и в суждениях существования, имеется всегда лишь один субъект. В суждениях об отношениях – более, чем один.

По характеру субъектов простые суждения делятся на единичные и множественные. В единичном суждении все термины, играющие роль субъектов,– единичные имена. В множественном суждении, по крайней мере, один из субъектов представляет класс предметов. В последнем случае обязательными частями суждения, наряду с субъектами и предикатом являются также кванторные слова – «всякий», «некоторые», «многие», «какой-нибудь» и т.п.– для каждого из субъектов, представляющих класс предметов. Слова этого рода указывают, относится ли то, что утверждается или отрицается в суждении, ко всем предметам соответствующего класса или к какой-то его части: «Студент Иванов успешно сдал некоторые предметы сессии», «Все планеты Солнечной системы вращаются вокруг Солнца», «Некоторые студенты не знают ни одного из иностранных языков». Конечно, возможны случаи, когда эти слова в тех или иных случаях опускаются, однако они должны, по меньшей мере, подразумеваться. Иначе вместо суждения, как уже отмечалось в § 6, имеем лишь некоторую высказывательную форму – аналог предиката как вида выражения в формализованном языке (Слово «предикат» мы употребляли раньше именно для обозначения выражений некоторого вида в формализованном языке (ЯЛП). В другом смысле, хотя и связанном с первым, мы употребляем его теперь для обозначения определенных частей простых суждений. В этом случае более точным является выражение «предикат суждения».),– которую нельзя оценить ни как истинную, ни как ложную.

Наряду с указанными основными частями суждений (субъектами, предикатами, кванторными словами) выделяют иногда в так называемых категорических суждениях (о них речь ниже) в качестве самостоятельной части связки двух типов: суть, не суть (есть, не есть, является, не является и т.п.) Термины этого вида являются указателем того, является ли суждение утвердительным или отрицательным. Например, «Все металлы суть простые вещества», «Ни один металл не есть сложное вещество». По существу, во втором случае имеем связку «не суть» («не суть (суть)» – множественное, а «не есть (есть)» – единственное число). Логически «Ни один металл не есть...» то же, что и «Все металлы не суть...».

Не бесполезно учесть существенное различие между понятиями «логическое подлежащее» (субъект суждения) и «логическое сказуемое» (предикат суждения), с одной стороны, и «грамматические (соответственно) подлежащее и сказуемое», с другой. Выделение первых существенно именно для понимания смысла суждения, тогда как грамматические категории часто не имеют к этому пониманию никакого отношения. Различение грамматических подлежащего и сказуемого имеет чисто формальное значение. Что дает, например, знание того, что в предложении «Порядочному человеку чуждо зазнайство» подлежащим является «зазнайство»? Ведь речь в этом суждении идет о порядочных людях и именно их хотят охарактеризовать. То есть логическим подлежащим (субъектом) данного суждения – при истолковании его как атрибутивного – является здесь, очевидно, «порядочный человек», а логическим сказуемым (предикатом суждения) «чуждо зазнайство». Хотя, возможно, правда, истолковать это высказывание и как суждение об отношении. Тогда субъектами будут «порядочный человек» и «зазнайство», а предикатом – «чуждо» (несовместимы). Как учит грамматика, в простом предложении может быть лишь одно подлежащее, хотя здесь, как и в известном высказывании «Гений и злодейство не совместимы» логических подлежащих оказывается два, а может быть и больше.

Из предыдущего примера мы видим, что имеется определенный момент относительности в различении суждений на атрибутивные и суждения об отношениях. Приведенное выше суждение об отношении «Земля вращается вокруг Солнца» может быть истолковано как атрибутивное – «Земля (субъект суждения) есть (связка) планета, которая вращается вокруг Солнца (предикат суждения)», а возможно и так: «Солнце (субъект) есть (связка) небесное тело, вокруг которого вращается Земля (предикат)». Здесь мы наблюдаем явление, которое можно понять, рассматривая суждения как знание, представляющее собой ответы на некоторые вопросы. Рассмотренное суждение, как суждение об отношении, представляет собой ответ на вопрос: как можно охарактеризовать Землю и Солнце с точки зрения их отношения друг к другу? Во втором случае (как атрибутивное) оно является ответом на вопрос: как можно охарактеризовать Землю по отношению к Солнцу? Если читатель помнит классификацию характеристик отдельных предметов (см. § 13), то он поймет, что предикат этого суждения – реляционное свойство Земли, а субъектом его является, очевидно, «Земля». В третьем случае, который, наоборот, представляет ответ на вопрос, как можно охарактеризовать Солнце по отношению к Земле? – субъектом является Солнце и утверждается также наличие у него реляционного свойства. Однако, если быть до конца последовательными, есть и четвертая возможность истолкования первоначального суждения: «Отношение между Солнцем и Землей (субъект суждения) есть (связка) отношение такое, что Земля вращается вокруг Солнца (предикат)». Это суждение является ответом на вопрос, каково отношение между Землей и Солнцем?

В каждом вопросе фиксируется что-то неизвестное в пределах чего-то известного. В суждении – в ответе на вопрос – неизвестное в вопросе выясняется как раз в предикате суждения. Субъект же суждения выражает то, что было уже известно (мысленно выделено). В последнем вопросе, например, известным является то, что есть какое-то отношение между Солнцем и Землей. Предикат же суждения, отвечающего на этот вопрос, указывает на характер этого отношения.

В традиционной логике употребительным было – при анализе суждений – понятие «логического ударения». Не вдаваясь в излишние подробности, скажем, что логическое ударение в суждении падает именно на субъект суждения, именно он указывает на то, что хотят охарактеризовать в суждении, хотя с точки зрения новизны знания «центр тяжести» приходится как раз на предикат суждения.

Выделение субъекта суждения существенно в процессах рассуждения. Он задает тему рассуждения. Одна из логических ошибок в рассуждении – в некотором смысле нарушение требования последовательности – может состоять в подмене одной темы другой, в скачке от одного к другому. Положим, что кто-то рассуждает о существительных, что существительные обозначают какие-то предметы, что они изменяются по падежам и числам и т.д. И вдруг в этой цепи рассуждения появляется фраза: «Глаголы отличаются от существительных тем, что они изменяются по лицам и временам»! Такой скачок затрудняет понимание хода рассуждений, а по поводу таких рассуждений говорят обычно, что речь человека сумбурна, страдает отсутствием последовательности. Ясно, что в данном случае естественнее – логичнее! – было бы сказать, в чем отличие существительных от глаголов, а не наоборот.

Все рассмотренные выше модификации и различия в истолковании суждения об отношении Солнца и Земли, понятия логического ударения, темы рассуждения и т.д. связаны с особенностями именно естественного языка, в них выражается определенная его гибкость, многообразие способов отражения одного и того же отношения. В формализованном же языке логики предикатов это многообразие исчезает. Отношения – двухместные, как в данном случае – отражаются в единой форме вида: Р(а₁, а₂)где а₁ и а₂ – индивидные константы для Земли и Солнца. Эта формула и есть перевод на ЯЛП рассматриваемого суждения именно как суждения об отношении. Данное истолкование его максимально информативно; все атрибутивные суждения, которые являются его модификациями, менее информативны. Это видно хотя бы из того, что все они получаются из суждения об отношении, а от каждого из них уже нет логического перехода к этому суждению. Из суждения об отношении мы можем получить другие суждения не только указанными выше способами, но и, например, перестановкой кванторов. Из суждения «Некоторые студенты не знают некоторых преподавателей», которое в ЯЛП имеет вид  можем получить –  то есть «Некоторые преподаватели и некоторые студенты таковы, что вторые не знают первых». Этой информации мы не можем извлечь, представляя исходное суждение как атрибутивное.

Мораль всего сказанного такова: нельзя, вообще говоря, сводить суждения об отношениях к атрибутивным.

КАТЕГОРИЧЕСКИЕ СУЖДЕНИЯ И ИХ ВИДЫ

В связи с некоторыми особенностями исторического развития логики и характером современной теории выводов (умозаключений) особо выделяют вид простых атрибутивных суждений, называемых категорическими суждениями. В первой в истории логики теории выводов, разработанной Аристотелем, рассматривались выводы именно из суждений этого типа. Эти формы выводов и в настоящее время выделяются особо в силу их распространенности и типичности в естественных, повседневных рассуждениях.

Категорические суждения – это множественные атрибутивные суждения; субъекты в них – всегда общее имя, таковым же – в стандартной форме выражения этих суждений – является и предикат. Более того, в такой же форме представления предикат, как правило, является описательным общим именем, то есть представляет собой знаковую форму, выражающую понятие. В стандартной форме в этих суждениях есть всегда и третий элемент – связка. А поскольку субъект есть общее имя, то всегда имеется и четвертый элемент структуры категорического суждения – кванторное слово.

В зависимости от того, относится ли утверждение (или отрицание) ко всем или не ко всем предметам соответствующего класса различаются общие и частные суждения (деление по количеству). Примеры общих: «Все жидкости суть упругие объекты», «Ни одна логическая операция не суть действие, осуществляемое без применения языка» и т.д. Частными являются: «Некоторые юридические законы суть нормативные акты, имеющие обратную силу», «Некоторые птицы не суть существа, улетающие зимой на юг» и т.п.

В зависимости от того, утверждается или отрицается нечто о мыслимых в субъекте предметах, суждение является утвердительным или отрицательным (деление по качеству). В стандартной форме – это означает различение суждений по характеру связки; в утвердительном – это суть (есть), в отрицательном – не суть (не есть) (см. только что приведенные примеры). При выражении суждений в естественном языке эти виды не всегда точно различимы, иначе говоря, это деление имеет некоторый относительный характер, в зависимости от того, к какой части суждения относится частица «не» (к связке или к предикату суждения). Так, суждение «Некоторые птицы не улетают зимой на юг», представленное выше как «некоторые птицы не суть существа, улетающие зимой на юг» может быть истолковано и как «Некоторые птицы суть существа, не улетающие зимой на юг». Для устранения возможных двусмысленностей в понимании суждений, что особенно существенно при анализе выводов, важно приводить их именно к стандартным формам.

Различая суждения одновременно по количеству и качеству, мы приходим к делению их на следующие виды:

общеутвердительные: стандартная (логическая) форма – «Все S суть Р»;

общеотрицательные: стандартная форма – «Ни одно S не суть Р»;

частноутвердительные: стандартная форма «Некоторые S суть Р»;

частноотрицательные: стандартная форма – «Некоторые S не суть Р», где S и Р – общие имена, соответственно, субъект и предикат суждения, суть (есть) и не суть (не есть) – связки, все (ни один) и некоторые – кванторные слова (количественные характеристики суждения). Все указанные типы суждений читатель без труда может найти среди приведенных выше суждений.

Подчеркнем еще раз, что эти формы представляют собой стандартные виды категорических суждений. Смысл суждения в стандартном виде состоит в том, что утверждается или отрицается принадлежность каждого или некоторых предметов S к классу предметов Р, или, более точно, тождество всех или некоторых предметов Sкаким-то предметам Р или отсутствие такового.

В нестандартной форме в суждении мы можем просто утверждать или отрицать наличие у всех или некоторых предметов S каких-то признаков Р. Сравните: «Все интеллигентные люди стремятся к самосовершенствованию» (нестандартная, так называемая атрибутивная – (см. § 13) – форма представления категорического суждения) и «Всякий интеллигентный человек есть существо, стремящееся к самосовершенствованию» (стандартная, понятийная форма). В случае таких (стандартных) преобразований в качестве предиката суждения появляется понятие; оно предполагает указание какого-либо (желательно ближайшего) рода предметов. Выявление его не всегда есть тривиальная задача, но в любом случае всегда можно взять наиболее широкий род: «некто» или «нечто» – «Юридические законы есть нечто, имеющее обратную силу» и т.п. Но нестандартность выражения суждения в естественном языке может состоять и в том, что не выявлены явным образом его субъект и предикат, а также и количественные характеристики. Приведение же к стандартной форме важно прежде всего в том отношении, что позволяет точным образом выразить и понять смысл того или иного высказывания. Что, например, мы утверждаем, говоря «Не все то золото, что блестит»? Конечно, здесь есть некоторый буквальный и переносный смысл. Буквальный: «Некоторые блестящие вещи не являются золотом». Переносный, очевидно, состоит в том, что не всякая внешне привлекательная вещь имеет действительную ценность. Но и здесь еще неясно, о чем и что именно утверждается об этом. В стандартной форме надо было бы сказать: «Некоторые внешне привлекательные вещи не суть такие объекты (предметы), которые представляют действительную ценность», то есть имеем стандартную форму частноотрицательного суждения «Некоторые S не суть Р».

Стандартизация той или иной мысли вообще есть выявление ее логической формы и представление ее именно в этой форме, то есть в такой форме, когда выявлены все ее составляющие и связь между ними, другими словами – отчетливо дана структура мысли. Впрочем, требование стандартизации высказываний и само понятие стандартной формы относится не только к категорическим суждениям.

Стандартная форма любого простого высказывания такова, что в ней выделены, во-первых, классы предметов или отдельные предметы, к которым относится утверждение или отрицание (субъекты суждения или логические подлежащие), во-вторых – в случае, если субъектами суждения являются классы предметов,– установлены количественные характеристики утверждений или отрицаний (кванторные слова), и, в-третьих, выделено, что именно утверждается или отрицается об этих предметах (предикат суждения или логическое сказуемое). Наряду с тем, что стандартизация имеет существенное значение для выяснения смысла выражений языка (в данном случае – предложений) и для правильного понимания их, она необходима также для осуществления определенных операций со смысловыми содержаниями этих выражений, для обеспечения возможности установления точных правил этих операций. Одним из способов осуществления стандартизации суждений является их перевод на язык логики предикатов, хотя бы с какой-то степенью точности.

 

ПРЕДСТАВЛЕНИЕ СМЫСЛА КАТЕГОРИЧЕСКИХ ВЫСКАЗЫВАНИЙ ПОСРЕДСТВОМ КРУГОВЫХ СХЕМ

Исходя из предыдущих рассмотрений относительно структуры смысла категорических суждений, эти структуры можно представлять в виде отношений между кругами, имея в виду, что сами круги представляют классы (объемы понятий), соответствующие субъекту и предикату.

 

 

Примечание. Поскольку в утверждении «Все S суть Р» не исключается и то, что «Все Р суть S», постольку круг Р не обязательно должен быть шире S – он может совпадать с S. В частноутвердительном суждении может не быть части S, которая находится вне Р, то есть возможно, что и «Все S суть Р». В частноотрицательном суждении также может не быть внутренней части S, то есть «Ни одно S не есть Р». Для желающих разобраться более детально в структурах категорических суждений см. ниже.

Имея перед собой задачу изображения структуры суждения как определенного типа знаний, следовало бы отобразить в круговых схемах и те моменты неопределенности этих знаний, которые имеют место в суждениях различных типов. С этой целью можно использовать пунктирное изображение некоторых частей границ классов. В таком случае схемы должны выглядеть по-иному.

Так, смысл общеутвердительного высказывания (Для высказываний схемы являются изображениями их смыслов. Для суждений, которые сами уже составляют смысл высказываний, схемы изображают структуру смысла.) может быть изображен в виде

 

 

Пунктир здесь означает неопределенность границ круга Р, состоящую в том, что может совпадать с S. Штриховка частей S выделяет S как субъект суждения и указывает на то, к какой именно части этого класса относится наше знание – утверждение или отрицание чего-либо в суждении. Это существенно, когда схема применяется именно для изображения структуры смысла высказывания, то есть структуры суждения как определенной формы знания. Вся схема как раз говорит о том, что класс S включается в Р, иначе говоря «Все предметы класса S принадлежат классу Р».

Для общеотрицательного суждения имеем:

 

 

«Все предметы S находятся вне класса Р и, очевидно, наоборот».

Для частноутвердительного суждения схема следующая

 

 

Пунктир S здесь соответствует выражению этих суждений «По крайней мере некоторые S суть Р» и указывает на возможность того, что внешняя часть круга Sявляется пустой, то есть не исключается, что «Все S суть Р». Пунктир же для окружности Р указывает на то, что все Р могут содержаться среди S.

Для частноотрицательного суждения имеем

 

 

Опять-таки пунктир указывает на возможность пустоты части S, находящейся внутри Р, то есть на возможность того, что ни одно S не есть Р.

Варианты, связанные с пунктирным изображением границ классов на схемах, можно трактовать (иногда так трактуют) как существование множества возможных схем для суждений одного и того же типа. При этом схемы представляют собой просто возможные отношения между понятиями S и Р, а множество схем для каждого типа суждений просто указывает, какие отношения между этими понятиями не исключает это суждение.

 

 

Для частноотрицательного суждения:

 

 

Эти схемы характеризуют информативность высказываний. Приведенные же выше схемы указывают на нечто большее: они характеризуют характер нашего знания. В частности, пунктирные части этих схем, как уже говорили, соответствуют тому, что в нашем знании, которое представляет то или иное суждение, является неопределенным.

 

ВЫДЕЛЯЮЩИЕ И ИСКЛЮЧАЮЩИЕ СУЖДЕНИЯ

Наконец, заметим, что к числу категорических суждений часто относят так называемые выделяющие категорические суждения видов:

 

¹Эта форма суждения не является естественной и в естественном языке не встречается

²То же.

 

Однако более точно суждения приведенных форм следует характеризовать не как категорические, то есть разновидность простых, а как некоторые сложные суждения.

Так, «Все S, и только S, суть Р» означает; «Все S суть Р и ни одно не-S не есть Р» то есть сложное суждение – конъюнкция двух высказываний. Например, суждение «Все млекопитающие животные и только млекопитающие являются теплокровными» имеет смысл: «Все млекопитающие животные суть теплокровные животные и ни одно не млекопитающее животное не является теплокровным».

Суждение вида «Все S, но не только S, суть Р» равнозначно: «Все S суть Р и некоторые не-S суть Р» Очевидно, что вроде бы простое по внешнему виду суждение «Все металлы, но не только они, проводят электрический ток» равносильно сложному: «Все металлы проводят электрический ток и некоторые неметаллы проводят электрический ток».

Первые два из частновыделяющих (вида 1) отличаются от других двух (вида 2) тем, что логическая константа «только» связана в них с субъектом, в двух других – с кванторным словом «некоторые» (первые можно было назвать субъектно-выделяющими, а вторые – кванторно-выделяющими суждениями). Для первых имеем эквивалентности:

Некоторые S, и только S, суть Р ≡ (Некоторые S суть Р) & (Ни одно не-S не суть Р). Например, «Некоторые кислоты и только они образуют соли» эквивалентно «Некоторые кислоты образуют соли и ни одна не кислота не образует соли».

Некоторые S, и только S, не суть Р ≡ (Некоторые S не суть Р) & (Все не-S суть Р). Например, «Некоторые лодыри и только они не сдадут этот экзамен» ≡ «Некоторые лодыри не сдадут этот экзамен» и «Все не-лодыри сдадут его».

Два других частновыделяющих вида 2 (кванторно-выделяющие) эквивалентны между собой и могут быть истолкованы как конъюнкция: (Некоторые S суть Р) & (Некоторые S не суть Р). Например, «Только некоторые студенты становятся профессорами» эквивалентно «Некоторые студенты становятся профессорами и некоторые студенты не становятся ими».

Определенное различие, которое чувствуется в формулировках этих суждений (хотя они объективно и эквивалентны), имеет психологический характер. В одном из них «Только некоторые S суть Р» центр тяжести падает на второй член конъюнкции «Некоторые S не суть Р», эквивалентный в свою очередь «Неверно, что все S сутьР». Поэтому все выделяющее суждение эквивалентно такому:

(Некоторые S суть Р) & (Неверно, что все S суть Р).

В суждении формы «Только некоторые S не суть Р» выделяется первая часть упомянутой конъюнкции (Некоторые S суть Р), эквивалентная «Неверно, что ни одно Sне суть Р». Принимая это во внимание, можно увидеть, что все выделяющее суждение этого вида эквивалентно: (Неверно, что ни одно S не суть Р) & (Некоторые S не сутьР).

Упомянутые психологические различия связаны со спецификой ситуаций, в которых высказываются эти суждения. Обычно эти суждения употребляются как возражения на необоснованные обобщения: если, например, студенты заявляют, что никто не сдаст логику, преподаватель может ответить: «Только некоторые не сдадут!», подчеркивая тот факт – первый член конъюнкции,– это некоторые сдадут. В случае же проявления излишней самонадеянности «Все сдадим!», естественно возразить: «Нет, только некоторые сдадут!», оттеняя второй член конъюнкции – «Некоторые не сдадут».

Как видим, логическая константа «только» употребляется как некоторый ослабленный аналог отрицания («Прямым» отрицанием в первом случае было бы суждение «Некоторые сдадут», а во втором – «Некоторые не сдадут»).

Исключающее суждение формы «Все S, кроме R, суть Р» выражает сложное суждение: (Все S, которые не являются R, суть Р) & (Ни одно R не есть Р). (Более детально, с учетом рода М понятии S, R, Р: «Все предметы класса М, обладающие свойством S и не обладающие свойством R, суть предметы М, обладающие свойствомР, и ни один предмет М, обладающий свойством R, не есть предмет М, обладающий свойством Р»).

Так, если кто-то говорит: «Все спортсмены, кроме боксеров, вызывают у меня симпатию», то фактически он утверждает: «Все спортсмены не-боксеры вызывают у него симпатию» (1) и «Ни один боксер симпатии у него не вызывает» (2). (С учетом М – особого рода понятий, играющих роль S, R, Р: 1. Все люди (М), являющиеся спортсменами (S) и при этом не являющиеся боксерами (R) есть люди (М), вызывающие у него симпатию (Р) и 2. Ни один человек (М), являющийся боксером (R) не есть человек (М), вызывающий у него симпатию (Р)).

Другая словесная формулировка исключающего суждения этого вида – сходная с выделяющим – «Среди S только R не суть Р».

Аналогичным образом выясняется смысл отрицательного исключающего суждения «Ни одно S, кроме R, не суть Р». Осуществить этот анализ предлагается самому читателю.

 

Упражнения

 

1. Выявите логическую форму суждений:

а) Многие юристы занимаются адвокатской деятельностью;

б) Спортсмены, достигающие больших успехов, затрачивают много времени на тренировки;

в) Потоки воды, текущие из мест более низких в места более высокие, не являются реками;

г) Есть такие люди, которые проявляют беспечность в жизненно важных ситуациях.

2. Представьте следующие высказывания как суждения об отношениях и образуйте из них возможные атрибутивные суждения:

а) Всякая мать любит своего ребенка;

б) Некоторые города расположены между Москвой и Одессой;

в) В темной комнате трудно найти черного кота.

3. Чем вызвана двусмысленность следующих предложений и как ее избежать? Какие простые суждения можно выделить в следующих высказываниях:

а) Когда Дубровский убил медведя, Троекуров не рассердился, а только велел снять с него шкуру;

б) Отец героя умер, когда ему было 28 лет;

в) Чернышевский пишет роман о направлениях деятельности демократической интеллигенции в крепости;

г) Боясь грозы, старуха спрятала голову под подушку и держала ее там, пока она не кончилась.

4. Определите вид следующих атрибутивных суждений и представьте их в стандартной форме (в необходимых случаях выявите их недостающие – подразумеваемые – смысловые части):

а) Народы мира не хотят войны;

б) Народ земного шара хочет мира;

в) Несколько дней бушевал ураган;

г) Не все современники динозавров вымерли;

д) Не шведы победили в битве под Полтавой;

е) Далеко не все руководители следуют принципу единства слова и дела.

5. Укажите, какие простые суждения содержатся в следующих высказываниях, определите их вид и представьте в эквивалентной форме:

а) Только металлы образуют соли;

б) Только существительные изменяются по падежам (какая часть этого высказывания является ложной?);

в) «Только тот достоин чести и свободы, кто каждый день за них идет на бой»;

г) Все водные животные, кроме китов и дельфинов, являются холоднокровными;

д) Ни один металл, кроме висмута, не сжимается при нагревании.

 

Виды сложных суждений

Напомним, что сложным является такое суждение, которое содержит в качестве своей правильной части некоторое (по крайней мере одно) другое суждение. Основные виды сложных суждений упомянуты и даны в определениях формул в ЯЛВ и ЯЛП. Это конъюнктивные – вида (А & В), дизъюнктивные – (A v B), импликативные –  и образованные из других суждений с использованием операции отрицания –  где А и В есть какие-то простые или, в свою очередь, сложные суждения. Например, к виду (А & В) будут относиться ((А & В) & С), как и (А & (В & С)), а также (А & (В v С)),  и т. п., где А, В, С – какие-нибудь суждения. Иначе говоря, вид сложного суждения определяется той логической константой, которая представляет последнюю операцию при образовании данного высказывания. Конечно, эта последняя операция не определяет всей структуры высказывания. Собственно основная задача анализа сложных суждений состоит не только в описании их логических структур, сколько в выяснении способов их возможных преобразований, особенно таких, результаты которых являются эквивалентными. Эквивалентные суждения иногда вообще даже не различают. Так, не различают, например, суждения (А & (В & С)) и ((А & В) & С), сводя их к виду А & В & С. Однако, строго говоря, это не точно: эти две знаковые формы выражают разные суждения. Но они равносильны (в силу закона ассоциативности конъюнкции) и отождествлять их можно, опуская скобки вообще, лишь тогда, когда нас интересует только истинностное значение суждения или (что то же) информация, которую выражает данная знаковая форма, а не само оно как смысл некоторого предложения. Аналогичным образом дело обстоит и для высказываний вида (A v В).

Следует обратить внимание на некоторые особенности выражения суждений в естественном языке. Во-первых, мы можем иметь здесь сложные суждения, составные смысловые части которых не выделены как особые части знаковой формы этого суждения. Пример такого рода мы уже приводили (относительно различения протонов и нейтронов – § 29).

Во-вторых, особенности высказываний в естественном языке проявляются и в том, что одни и те же логические константы могут иметь разные смыслы в различных ситуациях. Например, знаку «v» формализованного языка в естественном соответствует слово «или», но взятое в некотором определенном смысле – образованное с его помощью высказывание «А или В» указывает на наличие какой-нибудь из двух ситуаций А и В, не исключая возможность наличия той и другой (слабая дизъюнкция). Однако мы употребляем в естественной речи дизъюнкцию и в таком смысле, при котором высказывание «А или В» означает: «Имеет место ситуация А или В, но не обе вместе» (сильная, или строгая, дизъюнкция). Правда, в русском языке чаще в таких случаях употребляют слово «либо», то есть вместо «А или В» употребляют фразу «А либо В» (а иногда даже – «либо А, либо В»). Высказывание с сильной дизъюнкцией может быть выражено через слабую с использованием отрицания. А именно: «А либо В» выражает ту же информацию, что и следующие конъюнктивные высказывания: «А или В и неверно, что А и В», «А или В и неверно А или неверно В». Используя, как это часто делается в формализованных языках, для сильной дизъюнкции знак «v» и знак «≡» для отношения квивалентности (равнозначности, равносильности) между высказываниями, мы можем выразить приведенные эквивалентности точным образом:

 

 

Таким образом, утверждение с сильной дизъюнкцией является более сильным, то есть информативным, поскольку представляет собой конъюнкцию утверждений. Ничто не мешает нам, конечно, употреблять слабую дизъюнкцию, утверждая «А или В», когда ситуации А и В в действительности исключают друг друга. Мы можем это делать, когда хотим выразить информацию лишь о том, что есть лишь две эти возможности, оставляя открытыми вопрос о том, совместимы или несовместимы А и В (нас это не только может не интересовать, но мы можем даже этого и не знать). Если для решения той или иной задачи достаточно этого, то нецелесообразно даже употреблять более сильное утверждение «А либо В», поскольку при этом к существенному для решения именно этой задачи добавляется несущественное для него. А это затрудняет понимание рассуждения и утверждающему это больше вероятности ошибиться. К тому же, чем больше утверждается, тем больше надо и доказывать. Поэтому в таких ситуациях справедливым представляется принцип: «Не утверждай больше, чем нужно!»

 

 

По смыслу ясно, что как для сильной, так и для слабой дизъюнкции высказывание «А или В» эквивалентно «В или А», то есть или оба истинны или оба ложны. Это свойство дизъюнкции называется коммутативностью (перестановочностью).

Разные употребления имеют и союзы «и», «если..., то...», соответствующие конъюнкции («&») и импликации  в формализованных языках. Для конъюнкции, например, имеет место эквивалентность: A & В ≡ В & А. Однако явно не эквивалентны высказывания: «Человек М совершил правонарушение и понес наказание» и «Человек М понес наказание и совершил правонарушение». Здесь употребляется так называемая конъюнкция, для которой существенное значение имеет последовательность описания событий. Употребляя в формализованных языках «&», мы отвлекаемся от порядка событий в действительности и, конечно, это правомерно лишь в тех случаях, когда в самой действительности последовательность не является существенной. Конъюнкция в таком случае обладает свойством коммутативности как и дизъюнкция. То есть «А и В» эквивалентно «В и А» (А & В ≡ В & А).

Этим свойством не обладает логическая связка, рассматриваемая ниже – импликация  В русском языке вместо слова «и» для обозначения конъюнктивной связи высказываний А и В употребляются также: «А и В имеют место одновременно»; «Как А, так и В»; «А, хотя и В»; «Не только А, но и В»; «А несмотря на В»; «А, в то время, как В» и т.д. Ясно – по смыслу связки «и»,– что вместо одного сложного высказывания «А и В» мы можем высказать одно за другим два высказывания: «А» и «В» (то есть«А», «В»). Эти два случая в естественном языке часто даже трудно различить, какой из них имеет место. Часто это приходится решать по контексту.

Многообразные аналоги имеются в естественном языке также и для импликации  Основная знаковая форма, соответствующая высказыванию  в естественном языке: «Если А, то В», хотя часто употребляют такие: «Поскольку А, постольку В»; «Коль скоро А, то В»; «В, если А»; «А достаточно для В»; «В необходимо для А» или просто, опуская логическую связку, говорят: «Назвался груздем – полезай в кузов»; «Сказал А – говори В». Во всех таких случаях подразумевается: «Если А, тоВ». Эти случаи надо отличать от тех, когда словосочетание «если..., то ...» употребляется вместо союза «и» в совокупности с некоторым противопоставлением, например, «Если вчера было жарко, то сегодня хоть пальто надевай».

Однако и сама логическая связка «если..., то...» может иметь разные смыслы в естественном языке. Обычно указанный союз выражает связь между некоторыми свойствами предметов или связь между явлениями, событиями, процессами и т.п. (детерминированность, обусловленность одного другим) и истинность всего сложного суждения (в отличие от того, когда «если..., то...» представляет определенную ранее импликацию, которая называется «материальной импликацией») не зависит от истинностных значений составляющих его простых. Например, одинаково истинными будут утверждения: «Если сумма цифр числа 357 делится на 3, то и само это число делится на 3» и «Если сумма цифр числа 457 делится на 3, то и само это число делится на 3». Оба эти суждения истинны, поскольку оба они выражают действительно имеющуюся связь между указанными свойствами чисел (представленных в десятичной системе). При замене условной связи материальной импликацией, то есть при истолковании «если..., то...» как материальной импликации, оба эти суждения также будут истинными. Но истинным окажется также и утверждение: «Если сумма цифр числа 457 делится на 3, то это число делится на 5»,– хотя ясно, что нет никакой связи между делимостью суммы цифр числа на 3 и делимостью самого числа на 5. Данное же высказывание истинно согласно приведенным ранее (см. § 10) условиям истинности импликативных высказываний; в нашем случае – в силу ложности антецедента высказывания. Утверждение условной связи сильнее, чем утверждение «Если А, то В» в смысле материальной импликации: всегда, когда истинно первое – истинно и второе, но не наоборот. Употребляя материальную импликацию, мы отвлекаемся от связи между высказываниями по содержанию, то есть от связей между ситуациями, которые описывают эти высказывания. Это обусловливает некоторые «странности», которые иногда даже характеризуют как парадоксы материальной импликации. Однако, несмотря на это упрощение рассматриваемой логической связки, а именно даже благодаря этому упрощению, она оказывается весьма полезной для описания различных форм дедуктивных выводов. Заметим, что в настоящее время в логике построены и такие формализованные языки и аппарат дедукции, в которых импликация (обозначаемая обычно «→») адекватна указанной связке, «если..., то...». Языки этого рода полезны для выражения именно таких высказываний, где необходимо отразить наличие связей между ситуациями действительности, например, в формулировках законов науки. Логические исчисления указанных типов получили название релевантной логики (См., например, Войшвилло Е.К. Символическая логика. Классическая и релевантная.– М.: Высшая школа, 1989.).

 

Упражнения

 

1. Определите, какие из указанных высказываний являются сложными, и переведите их на язык логики высказываний, обозначив простые составляющие сложного суждения отдельными буквами:

а) Кто любит трудиться, тому без дела не сидится;

б) Он и рад бы косить, да некому косу носить;

в) Если некоторое число N оканчивается на 0 или на 5, то оно делится на 5 и если число не делится на 5, то оно не оканчивается ни на 0, ни на 5;

г) Есть ложь, не заслуживающая порицания;

д) Если на приговор подана жалоба или принесен протест, дело подлежит передаче в вышестоящий суд;

е) Кончив дело – гуляй смело или продолжай работать;

ж) Если какой-то человек сказал неправду, то он или не знает действительного положения дел или умышленно вводит в заблуждение других, но ни то и другое вместе;

з) Ни один прокурор не является адвокатом;

и) Какая бы ни была работа, если взялся за нее, то доводи до конца.

к) Если еще в прошлом веке автомобиль был роскошью, то в нынешнем – это средство передвижения.

 

Понятие необходимого и достаточного условия

Условная связь «если..., то...» будучи средством выражения законов науки, полезна также для выяснения важных с точки зрения логической культуры понятий необходимого и достаточного условия чего-либо.

Мы говорим, что обстоятельство А (признак, событие, явление и т.п.) является достаточным условием обстоятельства В, если и только если А и В связны между собой таким образом, что в каждом случае, когда имеется А, имеется и В, то есть для каждого случая истинно высказывание «Если А, то В».

Обстоятельство А является необходимым условием обстоятельства В, если и только если А и В связаны между собой таким образом, что в каждом случае при отсутствии А, отсутствует В, то есть в каждом случае истинно высказывание «Если неверно А, то неверно В» (это высказывание эквивалентно высказыванию «Если В, тоА»).

Из сказанного видно, что если А – необходимое условие В, то В – достаточное условие А, и наоборот. А из приведенного выше примера видно, что делимость суммы цифр числа на 3 есть достаточное условие делимости на 3 самого числа. Естественно в этом случае, как и во всех подобных, ставить вопрос, является ли оно необходимым? Известно из арифметики, что это действительно так.

С понятиями необходимых и достаточных условий в математике связаны понятия прямой и обратной теорем. Формулируя теорему вида «Если А, то В», устанавливают достаточность условия А для В. Установление же того, что имеет место и обратная теорема «Если В, то А» означает указание того, что А является и необходимым условием для В (поскольку «Если В, то А» равносильно «Если не-А, то не-В»). Имея теорему вида «Для всякого объекта некоторого класса (геометрических фигур, чисел и т. п.) верно, что если он обладает свойством А, то он обладает свойством В», ставят обычно вопрос, а верно ли обратное – «Если В, то А»? Если так, то мы имеем также и обратную теорему по отношению к первой. Подобные рассуждения относятся не только к математике. Теорема математики – это некоторый закон математики, аналогичные вопросы возникают по отношению к законам любой науки. Будучи выраженным либо в форме «Всякое S суть Р» (всякий предмет некоторого класса М, обладающий свойством S, обладает свойством Р) или в виде «Для всякого предмета класса М верно, что если он обладает свойством S, то он обладает свойством Р», он – при условии правильной формулировки закона – содержит указание достаточного условия S для существования Р. И, конечно, не лишен при этом познавательного значения вопрос: не верно ли и обратное? Естественно, само S может быть сложным свойством, хотя бы в том смысле, что оно является объединением множества свойств, и достаточным условием Р является именно совокупность свойств. Вспомним, например, закон классической механики: «Всякое тело (М), на которое не действует никакая сила или равнодействующая всех сил равна нулю (S), находится в покое или движется равномерно и прямолинейно (Р)». Но полезно, конечно, знать, что верно обратное: «Всякое тело, которое находится в покое или движется равномерно и прямолинейно, есть тело, на которое не действует никакая сила или равнодействующая всех сил равна нулю». Таким образом, признак, состоящий в том, что на тело не действует никакая сила или равнодействующая всех сил равна нулю(S(x)), является достаточным и необходимым для признака «тело покоится или движется равномерно и прямолинейно» (Р(х)).

 

Упражнения

 

1. Выясните, является ли достаточным и необходимым условием для указанного выше признака Р признак: «На тело не действуют никакие силы» (S₁)? (Точнее Р(х) иS₁(x), поскольку знаковыми формами признаков, как помнит читатель, являются предикаты).

2. Аналогичную задачу решите для признака «равнодействующая всех сил, действующих на тело, равна нулю» (S₁(x)).

Заметим, что вообще для любых двух признаков S(x) и Р(х) (относящихся к некоторому классу предметов М – области значений переменной х) справедлива классификация:

1) Один из них является достаточным и необходимым условием для другого или

2) достаточным, но не необходимым, или

3) недостаточным, но необходимым, или, наконец,

4) недостаточным и не необходимым.

Выше уже приведены примеры признаков достаточных и необходимых; читатель, только что выполнивший упражнение, наверное установил, каковы отношения междуS₁(x) и Р(х), а также между S₂(x) и Р(х). Для некоторых подскажем, что S₁(x), как и S₂(x), достаточен для Р(х), но не необходим.

Аналогично, незаконное хранение оружия достаточно для привлечения к уголовной ответственности, но, конечно, не является необходимым для этого. Но гласность, являясь необходимым условием демократии, не является в то же время достаточным, как и, например, повышение производительности труда для повышения уровня благосостояния общества. Между тем рост человека, его возраст и, конечно, пол не являются ни достаточными и ни необходимыми условиями для усвоения логики.

И, наконец, вспомним определение основного содержания понятий. Его составляет совокупность признаков, каждый из которых необходим, а все вместе они достаточны для решения вопроса о том, относится ли какой-нибудь предмет к объему понятия, то есть к классу обобщаемых предметов.

Знание самих понятий, необходимых и достаточных условий может быть весьма полезным для образования тех или иных понятий, для выяснения смыслов имен. При этом оно может избавить человека от хаотического и излишнего перечисления признаков предметов, способствовать минимизации тех данных, которые характеризуют тот или иной предмет или предметы некоторого вида. Именно требование указанной минимизации подразумевается обычно в обращении учителя к ученику или вообще к тому или иному человеку: «Выделяйте существенное», «Не нужно второстепенного, не идущего к делу» и т. п. Требования такого рода часто означают: укажите достаточные и необходимые признаки предметов данного класса.

 

Упражнения

 

1. К какому виду – с точки зрения необходимости и с точки зрения достаточности – принадлежат следующие условия:

а) делимость числа на 2 и на 3 для делимости его на 6;

б) активное участие общественности в борьбе с преступностью для ликвидации преступности;

в) мутации для естественного отбора;

г) круглая тень Земли на поверхность Луны для признания истинности утверждения о шарообразности Земли;

д) нагревание металлического стержня для его расширения;

е) наличие тренировок для установления рекордов;

ж) наличие дыма для огня;

з) знание предмета для получения отличной оценки по нему на экзамене;

и) истинность одного члена дизъюнкции для истинности всей дизъюнкции;

к) истинность обоих членов дизъюнкции для истинности всей дизъюнкции;

л) ложность антецедента для истинности импликации; м) ложность обоих членов дизъюнкции для ложности всей дизъюнкции;

н) ложность консеквента для истинности импликации.

2. Пользуясь определениями необходимого и достаточного условий, сформулируйте соответствующие суждения с употреблением связки «если..., то...» 

а) А есть необходимое условие для В;

б) В есть необходимое условие для А;

в) А есть необходимое, но не достаточное условие для В;

г) В есть достаточное, но не необходимое условие для А;

д) А не достаточное и не необходимое условие для В;

е) неверно, что А достаточное и необходимое условие для В;

ж) неверно, что А не достаточное условие для В или В не необходимое условие для А.

3. Какие суждения относительно достаточности или необходимости условий можно сформулировать исходя из истинности высказываний вида:

Связь между простыми суждениями со сложными субъектами и предикатами и сложными суждениями. Преобразование категорических суждений за счет расширения субъектов

Собственно, мы уже рассматривали примеры простых суждений со сложными субъектами или предикатами (возможно, конечно, и то и другое, то есть дизъюнкция здесь слабая). Это случаи, когда субъект или предикат суждения есть понятие, основное содержание которого составляет сложный предикат (сложную высказывательную форму). Таковым является суждение о каждом теле, на которое не действуют никакие силы или равнодействующая всех сил равна нулю,– субъект суждения, и для которого верно, что оно находится в покое или движется равномерно и прямолинейно,– предикат суждения. Другие примеры: «Всякое число, которое оканчивается на 0 или на 5, делится на 5»; «Всякое число, которое делится на 6, делится на 2 и на 3»; «Для всякого числа верно, что если оно оканчивается на 5 или на 0, то оно делится на 5». Едва ли надо разъяснять, что в этих суждениях субъект или предикат являются сложными.

Возможно, стоит обратить внимание читателя лишь на последний пример. Субъект здесь, очевидно, общее имя – «число», а предикат является сложным – импликативным: «Если оно (некоторое число х) оканчивается на 5 или на 0, то оно (это же число х) делится на 5». Читатель может, безусловно, сам убедиться, что все эти суждения являются простыми, поскольку ни в каком из них нельзя выделить такую часть, не совпадающую со всем суждением, которая в свою очередь была бы суждением. Однако для некоторых из этих суждений мы можем указать эквивалентные им сложные суждения. Так, суждение: «Всякое число, которое оканчивается на 0 или на 5, делится на 5» эквивалентно конъюнкции двух суждений: «Всякое число, которое оканчивается на 0, делится на 5» и «Всякое число, которое оканчивается на 5, делится на 5». Простое суждение: «Всякое число, которое делится на 6, делится на 2 и на 3» так же эквивалентно конъюнкции двух суждений: «Всякое число, которое делится на 6, делится на 2» и «Всякое число, которое делится на 6, делится на 3». Имеющиеся здесь отношения эквивалентности имеют общий характер, то есть справедливы для всех суждений, имеющих те же логические формы:

1. (Всякий предмет х из некоторой области D, имеющий свойство А или В, есть С (иначе, есть предмет х, обладающий свойством С)) = (Всякий предмет х из некоторой области D, который имеет свойство А, есть С) и (Всякий предмет х из некоторой области D, который имеет свойство В, есть С).

2. (Всякий предмет х из области D, обладающий свойством А, есть предмет х, обладающий свойствами В и С) = (Всякий предмет х из области D, обладающий свойством А, есть В) и (Всякий предмет х из области D, обладающий свойством А, есть С).

Аналогичным образом могут разлагаться на сложные суждения не только категорические, которые мы только что рассмотрели, но и суждения об отношениях.

Например, суждение вида  (Оно будет эквивалентным ). Впрочем, если учесть, что суждение об отношении может быть истолковано как атрибутивное, то этот случай сводится к первой из указанных эквивалентностей. Так, суждение об отношении «Для всякого предмета х, который обладает свойствами А или В,существует предмет у, обладающий свойством С, такой, что для них верно R(х, y)», мы сводим к атрибутивному со сложным объектом: «Всякий предмет х, обладающий свойством А или В, есть предмет такой, что существует предмет у, обладающий свойством С, к которому х находится в отношении R». Теперь оно разлагается как категорическое суждение со сложным дизъюнктивным субъектом (см. эквивалентность № 1).

 

Упражнения

 

1. Покажите, как можно разложить на сложные суждения приведенное выше простое суждение о теле, на которое не действуют никакие силы или равнодействующая всех сил равна нулю, и обратное ему.

2. Осуществите операцию разложения на сложные в отношении простого суждения: «Всякое слово, которое является существительным или прилагательным, изменяется по падежам и лицам».

По существу, как мы видим, разложению на сложные поддаются общие категорические суждения с дизъюнктивными субъектами или конъюнктивными предикатами («или» здесь – слабая дизъюнкция). Но не может быть разложено на сложное простое суждение вида  есть С(х)), например, «Всякое число, делящееся на 2 и на 3, делится на 6».

Суждение вида «Некоторые А или В суть С» эквивалентно дизъюнктивному сложному суждению: «Некоторые А суть С или Некоторые В суть С». Суждение же вида «Некоторые А суть В или С» эквивалентно: «Некоторые А суть В или Некоторые А суть С». Эти эквивалентности справедливы и для соответствующих отрицательных суждений, то есть частные суждения разлагаются на сложные лишь в случаях сложных дизъюнктивных субъектов или предикатов.

Далее, полезно иметь в виду следующие эквивалентности для категорических суждений (субъекты и предикаты которых есть понятия и при этом субъекты их не являются пустыми понятиями). Суждение вида «Всякий предмет х из области D, обладающий свойством S, суть предмет из этой же области, обладающий свойством Р» эквивалентно: «Всякий предмет D таков, что если он обладает свойством S, то он обладает также и свойством Р». Эта эквивалентность используется при переводах категорических суждений вида «Все S суть Р» на язык логики предикатов (ЯЛП), в котором оно получает форму выражения:  Но при таком переводе мы подразумеваем некоторую область возможных значений х – D, которая, естественно, должна подразумеваться и в исходном – переводимом – суждении. Суждение, получаемое при переводе, также категорическое, с субъектом – D и импликативным предикатом 

Общеотрицательное суждение «Ни один предмет из области D, обладающий свойством S, не есть предмет из D, обладающий Р» эквивалентно «Для всякого предметаD верно, что если он обладает свойством S, то он не обладает свойством Р». Соответственно этому суждение «Ни одно S не суть Р» на ЯЛП выражается: , при условии опять-таки, что область значений х D подразумевается в формулировке исходного суждения.

Для частных суждений имеем: «Некоторые предметы из области D, обладающие свойством S, суть предметы, обладающие свойством Р» эквивалентно «Некоторые предметы из области D таковы, что они обладают свойством S и Р».

«Некоторые предметы из области D обладающие свойством S, не суть предметы, обладающие свойством Р» эквивалентно «Некоторые предметы D таковы, что они обладают свойством S и не обладают свойством Р».

На основе этих эквивалентностей совершаются следующие переводы частных суждений на ЯЛП:

Некоторые S суть 

Некоторые S не суть  при этом – как и для общих суждений – область значений х должна подразумеваться в исходных суждениях.

• Таким образом, при указанных преобразованиях категорические суждения остаются категорическими, но с более широкими субъектами (область D) и при этом предикаты общих суждений преобразуются в импликативные, а частных – в конъюнктивные.

Однако такие преобразования, как уже было замечено, правомерны лишь при определенном условии, а именно: в том случае, когда понятие, играющее роль субъекта исходного категорического суждения, не является пустым, то есть имеет какое-то предметное значение. В противном случае не получается приведенных эквивалентностей. Например, суждение «Всякий человек, который не нуждается в пище, может жить не работая» (в стандартной форме: «Всякий человек, который не нуждается в пище, суть человек (лицо), который может жить, не работая») при указанном преобразовании приобретает форму: «Для всякого человека верно, что если он не нуждается в пище, то он может жить, не работая». Последнее суждение является, очевидно, истинным (тем более при понимании «если..., то...» как материальной импликации; в этом случае оно истинно в силу ложности, невыполнимости антецедента, то есть высказывательной формы «человек, не нуждающийся в пище», для любого человека). Исходное же суждение скорее всего нельзя признать истинным или ложным. «Истинность» и «ложность» есть соответствие или несоответствие нашей мысли действительности, а в действительности нет таких предметов, к которым относится утверждение.

В логике, правда, есть различные точки зрения относительно истинностных оценок высказываний с пустыми субъектами. Одна из них, которая приписывается Аристотелю, такова: утвердительные суждения с пустыми субъектами ложны, а отрицательные – истинны независимо от их содержаний. Согласий другой, все общие суждения с пустыми субъектами истинны, а частные ложны, опять-таки независимо от их содержаний. Но обе эти, как и другие, концепции представляют собой, по существу, произвольные соглашения и в каких-то случаях оказываются явно несостоятельными.

Например, вечный двигатель, по определению, есть двигатель, который работает без затраты энергии. Но, согласно первой концепции, суждение «Все вечные двигатели работают без затраты энергии» – ложно, хотя согласно второй,– оно истинно! Скорее всего такие суждения (с пустыми субъектами) следует считать неосмысленными, лишенными реального содержания, а в практике научного познания едва ли кто-нибудь будет высказывать такие суждения. Может, правда, оказаться, что мы не знаем, является ли некоторое понятие (и соответствующее общее имя) пустым или непустым. В физике, например, встречается такое понятие как «антиатом» (атом, устроенный «наоборот» по сравнению с обычным – с отрицательно заряженным ядром и вращающимися вокруг него положительно заряженными частицами, позитронами, вместо электронов). Но не зная, есть ли такие частицы, ни один ученый не скажет, например, что всякий антиатом при ионизации – при потере внешних позитронов – становится отрицательно заряженной частицей. Для выражения той мысли, которая фактически здесь имеется в виду, есть адекватная форма выражения, а именно: форма выражения категорического суждения с импликативным предикатом: «Для всякой частицы верно, что если она является антиатомом, то при ионизации она становится отрицательно заряженной».

Надо, конечно, заметить, что в науке для определенных целей, например, для обеспечения определенных обобщений, исключения мнимых оговорок употребляются суждения по-видимому и с пустыми субъектами. Так, в проективной геометрии вводятся понятия «бесконечно удаленной точки», «бесконечно удаленной прямой» и т.п. Многие имена, не обеспечивающие никаких реальных предметов, играют определенную инструментальную роль в науке. Таковы: системы координат, небесные и земные полюса, оси вращения и т.д. (см. § 12). Осмысленность суждений, относящихся к воображаемым объектом указанных типов, обусловлена тем, что они вводятся в определенной системе знаний и исходя из этой системы определяются условиями их истинности или ложности. А, соответственно, истинность или ложность во многих таких случаях не представляет собой соответствие или несоответствие действительности. Это – так называемые «истины по соглашению». Но сами соглашения, конечно, так или иначе научно обоснованы. Строго говоря, термины указанных типов, включенные в определенные системы знания, неправомерно уже считать пустыми, поскольку имеются определенные условия истинности или ложности утверждений, включающих такие термины.

 

Упражнения

 

1. Для каждого из следующих простых суждений укажите сложное, эквивалентное ему

а) всякое число, оканчивающееся на 0, делится на 6 и на 2;

б) некоторые числа, которые делятся на 2 или на 3, делятся на 5;

в) некоторые люди, не выполняющие своих обещаний, являются безвольными или непорядочными.

2. Укажите, как можно преобразовать следующие категорические суждения путем расширения их субъектов:

а) ни одно сражение, которое дал Суворов, не было проиграно;

б) многие реки текут с юга на север;

в) все имена прилагательные изменяются по падежам;

г) имелись подозреваемые, не проходившие по дактилоскопическим учетам.

 

Суждения ассерторические и модальные

В суждениях, как мы говорили, утверждается наличие или отсутствие той или иной ситуации. Однако некоторая мыслимая ситуация в действительности не просто наличествует или отсутствует, но существует случайно или необходимо и точно также отсутствует возможно или необходимо, то есть не является возможной. В другом плане, особенно, когда речь идет о ситуациях будущего, они характеризуются как возможные или необходимые, или как возможные или невозможные. Некоторые действия, поступки людей в обществе разрешены, другие даже обязательны или запрещены. А наши знания, суждения, например, могут быть доказаны или не доказаны, достоверны или проблематичны и т.д. и т.п.

В ассерторических суждениях мы отвлекаемся от подобных характеристик рассматриваемых ситуаций, здесь речь идет только о наличии или отсутствии чего-либо, то есть фиксируется лишь фактическое положение дел. Суждения, в которых имеются указанные и подобные им характеристики явлений, событий, процессов и т.д. (ситуаций вообще) называются модальными. Примерами ассерторических являются все суждения, которые рассматривались до сих пор (кроме приведенного закона механики). Модальными, например, являются все суждения, выражающие законы науки. Утверждая наличие каких-то связей в суждениях этого типа, мы утверждаем необходимый характер этих связей, хотя в некоторых случаях эта характеристика не выражается явно (как в упомянутом законе механики), но в любом таком случае, по крайней мере, подразумевается. Приведем еще примеры модальных суждений: «Ни один человек не может жить без пищи», «Некоторые люди не могут лгать», «Каждый гражданин обязан соблюдать законы», «Возможно, что существуют неземные цивилизации», «Обыск производится в присутствии понятых», «Споры о подследственности между властными участниками процесса не допускаются», «Иногда неудовлетворительные оценки (как, впрочем, и отличные) студенты получают на экзаменах случайно».

ТИПЫ И ВИДЫ МОДАЛЬНОСТИ

При различении модальностей мы выделяем типы, а внутри каждого типа – виды модальностей. Среди известных модальностей особо выделяются следующие типы.

Алетические модальности. К ним относятся такие характеристики – виды модальностей – как «необходимо», «возможно», «невозможно», «случайно». Впрочем, «невозможно» скорее надо охарактеризовать не как особый вид модальности, а просто как отсутствие (а в суждении – отрицание) возможности.

Деонтические модальности. Это характеристики действий, поступков людей в обществе. К ним относятся виды: «обязательно», «разрешено», «запрещено», «безразлично» (аналог алетической модальности «случайно»).

Эпистемические модальности. Это характеристики наших знаний. Среди них выделяются виды: «доказано», «опровергнуто», «возможно» (возможно допустить, что истинно некоторое высказывание), «не доказано и не опровергнуто» (для этого вида нет специального названия – это аналог «случайно» среди алетических модальностей). По другим основаниям выделяют такие виды: «знает», «верит», «убежден», «сомневается».

Характеристики некоторых приведенных видов модальностей различных типов могут быть уточнены путем указания взаимосвязи между ними. Для этого используем формы модальных высказываний. Пусть А – какое-то ассерторическое (не модальное) высказывание. Тогда «необходимо А» (указание на необходимость ситуации, утверждаемой в A) можно обозначать как НА (иногда применяют обозначение А). Возможность ситуации А выражается в виде MА (или ∆А), случайность можно обозначить как SA (или ∆А). Между высказываниями этих видов, а тем самым и характеристиками событий, имеют место соотношения:

 

 

Для высказываний с деонтическими модальностями приняты обозначения: «обязательно А» – ОА (обязательно делать так, чтобы истинно было А), «разрешено А» – РА (разрешено делать так, чтобы истинно было А), «запрещено А» – ЗА (запрещено делать так, чтобы было истинно А, то есть чтобы была ситуация А). «Запрещено А» здесь – аналогично алетической модальности «невозможно А», но если последняя по своему выражению означает просто отрицание возможности, то запрещение выступает как самостоятельная модальность. «Разрешено» естественно понимать не как наличие какого-то предписания, а как отсутствие запрещения. Это означает, что имеет место эквивалентность:

 

 

Эта эквивалентность выражает принцип демократического общества: «Разрешено все, что не запрещено». С учетом указанного понимания «разрешено» и «запрещено» между деонтическими модальностями могут быть установлены некоторые эквивалентности, идентичные приведенным выше для алетических модальностей:

 

 

Очевидно, не имеют места  и неверно, что . Если «безразлично А» обозначить как БА, то

 

 

Для эпистемических модальностей, если обозначить «доказано А» как ДА, «опровергнуто А» как ОпА», «возможно А» как ВА, «не доказано и не опровергнуто А» как СА, то имеем соотношения:

 

 

Для других видов эпистемических модальностей выделим одно определенное и важное соотношение: где «КА» – означает: «Некто знает, что имеет место ситуация А».

Для уяснения смысла алетических модальностей важно иметь в виду, что среди них в свою очередь различают физические (в широком смысле слова), или, что то же, фактические, онтологические модальности и модальности логического характера.

Физическая необходимость выражается в высказывании А, представляющем собой закон конкретной науки (физики, биологии, социологии и т.п.). Если В логически следует из физического закона А, то ситуация, которую оно представляет, также является всегда необходимой. И в силу этого истинно высказывание «фактически необходимо В» (НФБ). Например, согласно первому закону Кеплера, необходимо, что всякая планета Солнечной системы двигалась вокруг Солнца по эллипсу, в одном из фокусов которого находится Солнце. Но это же необходимо и для Земли и для Марса и т.д.

Физическую невозможность выражает высказывание, являющееся отрицанием какого-либо следствия из физического закона, включая, конечно, и отрицание самого этого закона науки, или эквивалентное такому отрицанию. Отсюда ясно, что высказывание выражает физическую возможность, если оно не является эквивалентным отрицанию какого-либо закона науки (а тем самым не является эквивалентным отрицанию какого-либо следствия закона науки, ибо отрицание следствия закона означает также и отрицание самого закона).

Высказывание А выражает физическую случайность, согласно введенному ранее определению, если физически возможно А и физически возможно не-А.

Логические модальности зависят от логических форм высказываний, то есть не зависят от значений дескриптивных терминов, входящих в него. О модальных высказываниях этого типа – применительно к высказываниям, выразимым в ЯЛВ и ЯЛП,– речь уже шла в разделах «Логика высказываний» и «Логика предикатов» (§ 10 и § 11). Для определения того, к какому виду логической модальности относится высказывание естественного языка, необходимо уметь выявить его логическую форму. Для этого необходимо выявить все его смысловые части – употребляемые в нем имена предметов, предикаторы, предметные функторы и логические константы,– которые могут быть не выражены явно. Для осуществления этой операции наиболее естественно перевести данное высказывание на язык логики высказываний или на язык логики предикатов.

Логически необходимым (выражающим логическую необходимость) является высказывание, истинное именно в силу своей логической формы. Это значит, что если в нем все дескриптивные термины заменить переменными соответствующих категорий (а тем самым отвлечься от значений имеющихся в высказывании дескриптивных терминов), то полученное выражение превращается в истинное при любых значениях дескриптивных переменных, то есть переменных, вводимых для дескриптивных терминов. Например, высказывание «латунь есть металл или латунь не является металлом» является логически необходимым, так как его логическая форма представляет собой универсально-общезначимое выражение. Напомним, что универсально-общезначимое выражение (соответственно-тождественно-истинное для ЯЛВ) – это законы логики и, значит, логически необходимыми являются такие высказывания, логические формы которых суть логические законы.

Логически невозможное высказывание представляет собой отрицание некоторого логически необходимого высказывания или эквивалентное таковому. Логически невозможным является, например, «латунь есть металл и неверно, что латунь есть металл»  И вообще, любое высказывание вида  («А и неверно, что А», где А, в свою очередь, любое высказывание) является, конечно, логически невозможным. Такие высказывания иначе называют логически противоречивыми.

Логически возможные высказывания те, что не противоречат закону логики, то есть не являются отрицанием какого-либо логически необходимого или эквивалентным таковому.

Логически случайные – такие, которые не являются логически необходимыми и не являются отрицаниями логически необходимых высказываний. Для всех видов логических модальностей также имеют место все приведенные эквивалентности и другие соотношения алетических модальностей. Если обозначить логическую необходимость высказываний А как Н_лА, логическую возможность – М_лА, а логическую случайность как С_лА, тогда имеем:

 

 

При рассмотрении отношений между высказываниями различных модальностей мы прибегали к операции отрицания высказываний. Она имеет важное значение в процессе познания. С этой операцией связан особый (наряду с уже известными нам отношениями логического следования и эквивалентности) вид отношений между суждениями – отношение противоречия. Таким образом, мы подходим к тому, чтобы, рассматривая указанную операцию с суждениями, обратиться к вопросу о том, какие существуют вообще виды отношений между суждениями.

 

Упражнения

 

1. Определите тип и вид модальности в следующих высказываниях:

а) всякий владелец вещи может продать ее;

б) хищение собственности противоправно;

в) всякое преступление наказуемо;

г) невозможно построить вечный двигатель;

д) доказана необратимость времени;

е) на Марсе возможна жизнь;

ж) возможно, что человек может прыгнуть выше своего роста.

2. Используя приведенные выше эквивалентности, выражающие связи между модальностями различных видов некоторого типа, выразите данные в следующих суждениях модальности через какие-нибудь другие, однотипные с ними:

а) обыск может быть произведен только в присутствии понятых;

б) разрешен проезд при зеленом свете светофора;

в) физическое тело, лишенное опоры, необходимо падает на землю;

г) нельзя курить в общественных местах.

Отрицание суждений. Виды отношений между суждениями

Попросту говоря, операция отрицания некоторого суждения А состоит в том, чтобы сказать: «Неверно, что А»  Однако обычно нас такой результат не удовлетворяет, и задача состоит не просто во внешнем отрицании, а в том, чтобы найти некоторые эквиваленты этого отрицания, в которых отрицание каким-то образом «пронесено» до некоторых частей этого суждения. Предположим, что в ходе расследования некто утверждает: «Неверно, что все члены преступной группы являются рецидивистами». Что же является верным и при этом эквивалентным исходному утверждению? Что ни один член преступной группы не является рецидивистом, или некоторые не являются рецидивистами, или некоторые являются? Подскажем, что исходное отрицательное высказывание эквивалентно – «Некоторые члены преступной группы не являются рецидивистами». Впрочем, читатель, наверно, и сам это определил. Предлагаем ему тогда решить аналогичный вопрос для суждения: «Неверно, что каждый любит кого-нибудь и ни один не любит всех». Если и это ему кажется весьма простым, тогда предлагаем еще одно. Положим, кто-то утверждает: «Поскольку в группе имеются неудовлетворительные результаты сдачи экзамена по логике, то либо по этому предмету плохо были прочитаны лекции, либо не была должным образом организована самостоятельная работа студентов». Другой заявляет, что это неверно. Что же с точки зрения последнего должно быть верным?

Решению подобных вопросов может существенно помогать знание так называемых правил образования противоположностей, точнее, контрадикторных противоположностей, или, что то же, противоречащих суждений.

 

 

Таким образом,  является противоречащим высказыванию А. В этом же отношении к нему находится любое высказывание В, эквивалентное  Ясно, что противоречащие (контрадикторно противоположные) суждения не могут быть одновременно оба истинными и не могут быть также оба ложными. Отсюда очевидно, что если исходное высказывание истинно, то противоречащее ему будет ложно и наоборот.

Для каждого высказывания А имеется неограниченное множество противоречащих ему высказываний, то есть эквивалентных  По упомянутым правилам «пронесения отрицания» мы получаем такие высказывания, эквивалентные  которые образуются посредством пронесения внешнего отрицания  в структуру самого высказывания А в сочетании с определенными преобразованиями структуры этого высказывания. Для применения указанных правил к некоторому высказыванию необходимо выявление логической формы высказывания А. Наиболее эффективный способ выполнения этой операции состоит в переводе данного высказывания на ЯЛВ или ЯЛП. Для всех высказываний, кроме категорических, такие переводы не представляют собой существенной перестройки их структур. Что касается категорических суждений, то мы уже говорили, что их знаковые формы являются специфическими для естественного языка, поэтому, формулируя правила пронесения отрицания, мы особо выделяем эти суждения, имея в виду при этом, что они представляются в стандартных формах. Для остальных высказываний эти правила уже сформулированы в §§ 10, 11 (см. «Законы образования контрадикторной противоположности»). Для удобства пользования напомним их еще раз:

 

 

Примеры

 

1. Возьмем суждение «Некоторые люди не заинтересованы в высоких заработках». Его контрадикторная противоположность: «Неверно, что некоторые люди не заинтересованы в высоких заработках». Задача состоит в том, чтобы найти высказывание, эквивалентное последнему, но без внешнего отрицания. Стандартная форма здесь, очевидно, такова «Некоторые S не суть Р» (неверно, что некоторые люди не есть лица, заинтересованные в высоких заработках. По правилу (для частноотрицательных суждений) имеем, что это эквивалентно: «Все S суть Р», то есть «Все люди заинтересованы в высоких заработках» (в стандартной форме: «Все люди есть лица, заинтересованные в высоких заработках»).

Читатель может сомневаться, истинно ли исходное суждение, противоречащее которому мы образовали. В данном случае для нас это не имеет значения. Важно лишь учитывать, что если оно истинно, то полученная нами его контрадикторная противоположность ложна и наоборот, если исходное высказывание ложно, то противоречащее ему истинно.

2. «Неверно, что можно курить в местах, где может возникнуть пожар». Выражение, стоящее здесь под отрицанием «неверно, что...») является, очевидно двусмысленным. Возьмем два варианта: «Нельзя курить во всех местах или в некоторых...». В первом случае, приводя суждение под отрицанием к стандартной форме, имеем: «Неверно, что все места, где может возникнуть пожар, суть места, где можно курить», то есть «Все S суть Р». По правилу получаем, что это эквивалентно: «Некоторые S не суть Р», то есть «Некоторые места, где может возникнуть пожар, не суть места, где можно курить».

Во втором случае наше отрицательное высказывание, имеющее вид «Неверно, что некоторые S суть Р» эквивалентно: «Ни одно S не суть Р» («Ни одно место, где может возникнуть пожар, не суть место, где можно курить»).

 

 

Упражнения

 

1. Образуйте контрадикторную противоположность следующим категорическим суждениям, приводя их к стандартной форме:

а) никакой идеолог не может находиться вне влияния классовых интересов;

б) многие учителя не имеют высшего образования;

в) бывают океаны с пресной водой;

г) не может быть свободен народ, угнетающий другие народы;

д) «Блажен, кто посетил сей мир в его минуты роковые».

2. Укажите противоречащие суждения тем, что приведены в начале этого параграфа для самостоятельного решения.

 

ОСНОВНЫЕ ВИДЫ ЛОГИЧЕСКИХ ОТНОШЕНИЙ МЕЖДУ ВЫСКАЗЫВАНИЯМИ

Говоря о видах отношений между высказываниями, различают отношения логические и фактические. Для каждого вида логического отношения есть некоторый аналог фактического отношения. Первые зависят от логических форм высказываний, вторые – от их конкретных содержаний. Мы ограничимся здесь в основном логическими отношениями. Это значит, что, рассматривая отношения между конкретными высказываниями, мы должны отвлекаться от их конкретных содержаний (а значит, и от того, являются ли взятые высказывания истинными или ложными).

Мы уже рассматривали такие виды отношений, как логическое следование, эквивалентность, противоречие, называемое также контрадикторной противоположностью. Это наиболее важные виды отношений, имеющие существенное значение в научном познании и практической деятельности. К ним следует добавить также отношение контрарной противоположности.

Высказывания А и В находятся в отношении контрарной противоположности, если и только если В эквивалентно отрицанию С  где С – следствие А, но не эквивалентно ему (то есть 

Более простым, равнозначным, образом это отношение может быть определено так:

Высказывания А и В контрарно противоположны, если и только если никакие высказывания, которые имеют те же логические формы, что А и В, не могут быть вместе истинными, но могут быть вместе ложными. Таковы, например, высказывания вида «Все S суть Р» и «Ни одно S не суть Р». Очевидно, что здесь «Ни одно S не суть Р», согласно вышеприведенным правилам пронесения отрицания, эквивалентно отрицанию «Некоторые S суть Р», а «Некоторые S суть Р» (высказывание С, фигурирующее в определении, является следствием суждения «Все S суть Р» и при этом не эквивалентно ему).

Содержательно ясно, что суждение вида «Все S суть Р» и «Ни одно S не суть Р» не могут быть оба истинными, но могут быть оба ложными. Как видим, отличие контрарной противоположности от контрадикторной состоит в том, что контрадикторно противоположные суждения не могут быть не только оба истинными, но и оба ложными. Для контрарных же суждений возможность ложности обоих не исключена.

Полезно также иметь в виду отношения более широкого характера. Это отношения совместимости (или несовместимости) высказываний по истинности, а также совместимости (или несовместимости) их по ложности.

Совместимы по истинности такие высказывания А и В, которые могут быть оба истинными. Иначе, и в некотором смысле более точно, А и В совместимы по истинности, если и только если неверно, что из А следует  Значит, А и В несовместимы истинности, если и только если из А логически следует  Совместимость высказываний по истинности в логике иногда называют просто «совместимостью высказываний».

Высказывания А и В совместимы по ложности, если и только если они могу быть оба ложными.

Во избежание недоразумений еще раз подчеркнем, что вместо выражения «высказывания А и В могут быть оба ложными или истинными» точнее надо было бы употребить выражение: «какие-нибудь высказывания, имеющие те же логические формы, что А и В, и, возможно, конечно, сами А и В, могут оказаться ложными (истинными)».

 

 

Читатель легко убедиться, что отношения логического следования и эквивалентности – это виды отношения совместимости по истинности, а контрарная и контрадикторная противоположности – виды отношения несовместимости по истинности.

Ясно, что знание более общего отношения (совместимость, несовместимость по истинности или по ложности) может само по себе быть полезным в процессе познания, поскольку нередко нам важно решить вопрос только о том, могут ли какие-нибудь высказывания быть вместе истинными или вместе ложными. Установив, например, что высказывания не могут быть вместе истинными, можем заключить, что, по крайней мере, одно из них ложно, а при наличии знания о том, что одно из них истинно, сделать вывод о ложности другого.

Внимательный читатель должен заметить, что данное здесь перечисление видов отношений между высказываниями не есть классификация видов, хотя бы потому, что члены приведенного перечня видов отношений не исключают друг друга. Таковы, например, отношения логического следования и эквивалентности. Видом отношения, соподчиненного эквивалентности, является так называемое отношение логического подчинения между высказываниями. В этом отношении находятся высказывания А и Втакие, что из А следует В (А ╞ В), но неверно, что из В следует  Для логической же эквивалентности А и В, как мы знаем, имеет место следование в обе стороны ((А ╞ В) & (В ╞ А)).

Для осуществления классификации среди высказываний, совместимых по истинности, нужно было еще указать вид отношения между высказываниями А и В,аналогичный отношению перекрещивания между объемами понятий. Перекрещивающимися высказываниями являются такие А и В, которые совместимы по истинности (при аналогичном отношении между понятиями – пересечение объемов понятий не пусто!), но неверно, что из А следует В, и неверно, что из В следует А. Таковы, например, любые высказывания вида «Некоторые S суть Р» и «Некоторые S не суть Р» или 

Как мы видели, все виды отношений определимы посредством понятия логического следования, что еще раз доказывает фундаментальный характер этого понятия в логике. Учитывая известную нам связь между логическим следованием и законами логики, отношение А ╞ В в этих определениях везде можно заменить на  Если теперь в этих определениях утверждение  – утверждение об общезначимости  – заменить конкретным высказыванием  то получаем понятие фактического отношения для конкретных высказываний А₀ и В₀, соответствующее данному логическому отношению, и где А и В суть логические формы данных конкретных высказывании A₀ и B₀. Так, аналогом логического следования между А₀ и В₀ является такое отношение между ними, которое характеризуется тем, что истинна импликация . Аналогом логического подчинения А₀ и В₀ является отношение, которое характеризуется тем, что  истинно, но  не истинно. Если же истинны обе эти импликации, то имеем отношение фактической эквивалентности (равнозначности) высказываний. Аналогом отношения противоречия будет отношение, для которого характерна истинность импликаций: 

Обратим внимание читателя, что для фактических отношений не подходят выражения типа: «Высказывания могут быть оба истинными» или «Не могут быть истинными», поскольку при учете конкретного содержания высказывания каждое из них уже истинно или ложно. Поэтому при характеристике фактических отношений должны учитываться истинностные значения высказываний.

ЛОГИЧЕСКИЕ ОТНОШЕНИЯ МЕЖДУ КАТЕГОРИЧЕСКИМИ СУЖДЕНИЯМИ

Обычно особо выделяют логические отношения между категорическими суждениями, ибо в традиционной логике при анализе отношений между суждениями имели в виду в основном категорические суждения, то есть суждения следующих видов:

Все S суть Р (тип А).

Ни одно S не суть Р (тип Е).

Некоторые S суть Р (тип I).

Некоторые S не суть Р (тип О), как говорят, с одинаковой материей, то есть с одними и теми же субъектами и предикатами. Эти отношения изображают посредством так называемого «логического квадрата»:

 

 

По верхней горизонтали суждения типа А и Е контрарно противоположны, то есть несовместимы по истинности: они не могут быть одновременно истинными (но могут быть одновременно ложными; сравни: «Все люди курят» и «Ни один человек не курит»).

По нижней горизонтали суждения типа I и О находятся в отношении «перекрещивания» (обычное название – «субконтрарность»). Они несовместимы по ложности, то есть не могут быть одновременно ложными (но могут быть одновременно истинными).

По обеим вертикалям – отношение логического подчинения: суждение типа А подчиняет I, a I подчинено А; аналогично для суждений типа Е и О соответственно. Для этого отношения характерно два свойства: 1) если истинно общее суждение, то истинно и подчиненное ему частное; 2) если ложно частное суждение, то ложно и соответствующее ему общее.

Отношение между суждениями, находящимися в концах диагоналей,– между А и О, Е и I – отношение контрадикторной противоположности (противоречия). Читатель без труда может охарактеризовать это отношение как такое, в котором эти суждения не могут быть одновременно истинными и не могут быть одновременно ложными.

 

Упражнения

 

1. Используя правила «пронесения отрицания», укажите суждения, эквивалентные следующим:

а) не все существительные изменяются по падежам;

б) неверно, что ни один студент нашей группы не имеет высшего образования;

в) неверно, что некоторые люди прочитали все художественные произведения;

г) нет дыма без огня;

д) неверно, что все юристы и только они способны правильно составить текст договора;

е) неверно, что все люди, кроме лгунов, являются честными.

2. Используя правила пронесения отрицания, сформулируйте суждения, находящиеся в отношении противоречия к следующим:

а) все существительные изменяются по падежам;

б) встречаются люди, не прочитавшие за всю свою жизнь ни одной книги по логике;

в) если не совершишь преступления, то не будешь и наказан;

г) если предприятие нерентабельно, то на нем плохо организована работа или устарело оборудование;

д) если слово является именем существительным, то оно изменяется по падежам и по числам;

е) либо каждый любит кого-нибудь и ни один не любит всех, либо некто любит всех и кто-то не любит никого;

ж) ни один человек, кроме спортсмена, не может пробежать марафонскую дистанцию.

3. Установите, являются ли эквивалентными следующие высказывания:

а) сын работает на заводе, а дочь учится в школе. Неверно, что сын не работает на заводе или дочь не учится в школе;

б) если слово ставится в начале предложения, то оно пишется с большой буквы. Неверно, что слово ставится в начале предложения и при этом не пишется с большой буквы;

в) если на улице не идет дождь, то на улице не сыро. Если на улице не сыро, то не идет дождь;

г) если Н. является следователем, то он является юристом. Если Н. не является следователем, то он не юрист.

д) если человек лжет, то он не является честным. Если человек является честным, то он не лжет.

 ВЫВОДЫ (УМОЗАКЛЮЧЕНИЯ)

Общая характеристика. Вывод (умозаключение) (То, что в современной логике называют процедурой вывода, в традиционной логике обозначали термином «умозаключение». Последнее менее точно, поскольку подразумевает фактически психологическую трактовку процедур. Но в ряде случаев мы сохраняем это обозначение, так как для многих – начавших изучение логики с традиционной – является более привычным.) – это способ получения нового знания на основе некоторого имеющегося.Он представляет собой переход от некоторых высказываний А₁, ..., А_n (n ≥ 1), фиксирующих наличие некоторых ситуаций в действительности, к новому высказыванию В и соответственно к знанию о наличии ситуации, которую описывает это высказывание. Например, в механике известно, что у всякого тела, плотность которого одинакова во всех его частях, геометрический центр и центр тяжести совпадают. Известно также (в результате астрономических наблюдений), что у Земли эти центры не совпадают. Отсюда естественно заключить, что плотность Земли не является одинаковой во всех ее частях. Едва ли нужно специально говорить о значении этой операции в познавательной и практической деятельности. Посредством умозаключений мы получаем приращение знаний, не обращаясь к исследованию предметов и явлений самой действительности, имеем возможность открывать такие связи и отношения действительности, которые невозможно усмотреть непосредственно.

Переход от некоторых высказывание А₁, ..., А_n (посылок умозаключения) к высказыванию В (заключению) в умозаключении может совершаться на основе интуитивного усмотрения какой-то связи между А₁, ..., А_n (n ≥ 1) и В – такие умозаключения называют содержательными; или путем логического выведения одного высказывания из других – это умозаключения формально-логического характера. В первом случае оно представляет собой, по существу, психический акт. Во втором случае его можно рассматривать как определенную логическую операцию. Последняя и является предметом изучения логики.

Содержание умозаключения может быть более или менее развернутым. Так, из того, что над землей низко летают ласточки, люди заключают часто, что завтра будет плохая погода. Это умозаключение можно развернуть, выясняя, в чем именно состоит связь между ситуацией, которая фиксируется в посылке, и той, на которую указывает заключение. А именно, если объяснить, почему одно из наблюдаемых явлений (низкий полет ласточек) указывает на существование другого (будет плохая погода). В результате анализа получаем последовательность переходов от одних явлений к другим: ласточки летают низко потому, что мошкара, за которой они охотятся, летает низко над землей. А это происходит в свою очередь потому, что в воздухе имеется повышенная влажность, от которой насекомые намокают и опускаются к земле. Наличие же повышенной влажности предвещает дождь, а, следовательно, и ненастье. Как видим, при развертывании исходного умозаключения появляются новые посылки. Кстати, полезно обратить внимание, что в данном случае движение мысли идет в основном от следствий явлений к их причинам.

Это полезно заметить потому, что в учебниках по логике нередко можно найти утверждение, что в наших содержательных рассуждениях движение мысли происходит от причин к их следствиям. Как видим, это не всегда так. Таким образом, отношение между посылками и заключением отличается от отношения причина – следствие (см. § 40).

В содержательных умозаключениях мы оперируем, по существу, не с самими высказываниями, а прослеживаем связь между ситуациями действительности, которые эти высказывания представляют. Это и отличает содержательные умозаключения от умозаключений как операций логического характера, называемых иногда формализованными умозаключениями. В этих умозаключениях операции совершаются именно над высказываниями самими по себе, причем по правилам, которые вообще не зависят от конкретного содержания высказываний, то есть от значения дескриптивных терминов. Для их применения необходимо учитывать лишь логические формы высказываний (см. «Исчисление высказываний» и «Исчисление предикатов» – §§ 10, 11). Благодаря этому для умозаключений подобного типа мы имеем также четкие критерии их правильности или неправильности. Тогда как для содержательных умозаключений нет никаких определенных критериев этого рода и всегда возможен спор – рассуждает ли человек правильно или нет. Именно формализованные умозаключения являются предметом изучения логики. И именно их мы имеем в виду в дальнейшем.

Переход от содержательного умозаключения к формальнологическому, то есть формализация умозаключений, осуществляется посредством выявления – и явной фиксации ее в виде высказываний – всей информации, которая явно или неявно используется в содержательном рассуждении. Так, в примере с ласточками неявно используемая информация может быть выражена в общих суждениях: «Всегда, когда мошкара опускается к земле, опускаются и ласточки, охотящиеся за ней», «Всегда, когда намокает волосяной покров насекомого, то оно опускается к земле» и т. п. При решении того или иного уравнения, процесс которого представляет собой содержательное рассуждение, также подразумеваются какие-либо посылки – общие утверждения специально-математического, а не логического характера, например: «Если к обеим частям уравнения прибавить (или вычесть) одно и то же число, то равенство сохраняется. Равенство сохраняется также при умножении обеих частей на одно и то же число и при lелении их на одно и то же число, отличное от нуля».

Структура и основные виды умозаключений. Умозаключение и отношение логического следования. В умозаключении, как мы уже говорили, различают посылки – высказывания, представляющие исходное знание, и заключение – высказывание, к которому мы приходим в результате умозаключения.

В естественном языке существуют слова и словосочетания, указывающие как на заключение («значит», «следовательно», «отсюда видно», «поэтому», «из этого можно сделать вывод» и т.п.), так и на посылки умозаключения («так как», «поскольку», «ибо», «принимая во внимание, что...», «ведь» и т.п.). Представляя суждение в некоторой стандартной форме, в логике принято указывать вначале посылки, а потом заключение, хотя в естественном языке их порядок может быть произвольным: вначале заключение – потом посылки; заключение может находиться «между посылками». В приведенном в начале главы примере посылками служат два первых высказывания, а заключением – третье высказывание («плотность Земли не одинакова во всех ее частях»).

Понятие умозаключения как логической операции тесно связано с понятием логического следования (см. §§ 10, 11). Учитывая эту связь, мы различаем правильные и неправильные умозаключения.

Умозаключение, представляющее собой переход от посылок А₁, ..., А_n к заключению В, является правильным, если между посылками и включением имеется отношение логического следования, то есть В является логическим следствием А₁, ..., А_n (n ≥ 1). В противном случае – если между посылками и заключением нет такого отношения – умозаключение неправильно.

Естественно, что логику интересуют лишь правильные умозаключения. Что же касается неправильных, то они привлекают внимание логики лишь с точки зрения выявления возможных ошибок.

В делении умозаключений на правильные и неправильные мы должны различать отношение логического следования двух видов – дедуктивное (рассмотренное выше – §§10, 11) и индуктивное – (см. часть II этой главы). Первое гарантирует истинность заключения при истинности посылок. Второе – при истинности посылок – обеспечивает лишь некоторую степень правдоподобия заключения (некоторую вероятность его истинности). Соответственно этому Умозаключения делятся на дедуктивные и индуктивные. Первые иначе еще называют демонстративными (достоверными), а вторые – правдоподобными (проблематичными). Заметим, что в приводившемся примере с ласточками переход от наличия высокой влажности к выпадению осадков является лишь вероятностным умозаключением.

Выше (§§ 10, 11) мы рассмотрели связь отношения дедуктивного логического следования с понятием логического закона, а также и логического вывода. Напомним, наличие логического вывода А₁, ..., А_n ├ В указывает на то, что логическим законом является высказывание вида  Таким образом оказывается, что основу правильных дедуктивных умозаключений составляют определенного вида законы логики.

Логический вывод можно охарактеризовать как некоторую последовательность умозаключений, хотя – поскольку речь идет о выводах в формализованных языках – его определяют просто как последовательность высказываний, избегая возможности привнесения психологических моментов в предмет логического анализа. В естественных языках мы имеем также некоторые подобия выводов, представляющих собой именно последовательности умозаключений. Обычно эти выводы не являются формализованными. Это проявляется в том, что в них могут опускаться и лишь подразумеваться некоторые посылки и логические переходы от одного к другому. Подобные выводы мы имели, например, в доказательствах теорем геометрии, при решении уравнений и т.д. Вообще, применяя термин «умозаключение», мы имеем в виду выводы именно в естественных языках. При этом выделяем именно такие умозаключения, которые являются так или иначе логически обоснованными.

 

ДЕДУКТИВНЫЕ ВЫВОДЫ

Следуя сложившейся в логике традиции, мы выделяем в качестве видов умозаключений лишь некоторые основные правильные формы таковых, наиболее часто встречающиеся в повседневной практике мышления. Один из этих видов – так называемые выводы из сложных высказываний – по существу представляют собой правила вывода, рассмотренные уже в логике высказываний (см. § 10). Другие – выводы из категорических высказываний – в логике предикатов (§ 11) и представляют собой, как мы уже отмечали, специфические формы выводов в естественных языках. Те и другие формы по упоминавшейся традиции называют силлогизмами (от греческого названия дедуктивных умозаключений).

§ 35. Выводы из сложных высказываний (выводы на основе свойств логических связок)

К подобным высказываниям относятся следующие простые формы (Простое умозаключение – это умозаключение, не разложимое на какие-то другие умозаключения.)(схемы) умозаключений.

Условно-категорический силлогизм, включающий два правильных модуса (разновидности):

 

 

Одна из посылок, как мы видим, здесь – условное высказывание. Согласно традиционной терминологии, высказывание А в его составе есть основание данного условного высказывания, В – его следствие (по современной терминологии – это соответственно антецедент и консеквент условного высказывания). В соответствии с этим само умозаключение в первом случае характеризуют как движение мысли от утверждения основания условного высказывания (посылка А) к утверждению его следствия (заключение В). Второй модус согласно той же терминологии представляет собой движение мысли от отрицания следствия условного высказывания (посылка не-В) к отрицанию его основания (заключение не-А). А и В здесь в свою очередь какие-то высказывания, но не обязательно категорические, как предполагалось в традиционном учении (откуда и произошло название данных модусов). Эти высказывания могут быть любыми, в том числе и сложными.

 

Примеры

 

 

Рассмотрим умозаключение:

«Если сумма цифр числа 346 не делится на 3, то оно не делится на 3. Сумма цифр числа 346 не делится на 3. Следовательно, число 346 не делится на 3». Это умозаключение также представляет собой утверждающий модус, несмотря на отрицательный характер второй посылки, ведь она является утверждением основания условного высказывания, которое, как можно увидеть, носит отрицательный характер.

Проанализируем еще одно умозаключение: «Если число 3576 является простым, то оно не делится на 3. Число 3576 делится на 3. Следовательно, число 3576 не является простым» – оно тоже представляет собой отрицающий модус, несмотря на утвердительный характер второй посылки, поскольку она эквивалентна отрицанию следствия условного высказывания: «Число 3576 не делится на 3». Строго говоря, мы принимаем здесь еще и правило двойного отрицания, то есть осуществляем переход от «неверно, что не-В» к «В».

В более формализованном виде – по сравнению с данным в начале – схемы этих умозаключений соответственно таковы:

 

 

Очевидно, что возможно бесконечное множество вариаций (конкретизации) исходных схем.

 

Упражнение

 

Установите, к каким из указанных модусов (утверждающему или отрицающему) относятся умозаключения следующих видов, приведите примеры умозаключений таких видов:

 

 

¹Вспомните закон де Моргана: «неверно (А и В)» эквивалентно «неверно А или неверно В» 

Используя введенную ранее символику (см. «Язык логики высказываний» – § 10) и рассматривая «Если..., то...» как матермальную импликацию  исходные схемы утверждающего и отрицающего модуса условно-категорического силлогизма можем представить в виде:

 

 

Очевидно, что им соответствует отношение логического следования:  и логические законы  Убедитесь в этом, используя данный ранее табличный метод (см. § 10) (Возможность такой проверки дает современная символическая логика – в традиционной логике не было способа доказательства правильности описываемых умозаключений.).

Имея в виду выработку навыков правильных умозаключений, полезно обратить внимание и на неправильные формы условно-категорического силлогизма, тем более, что в практике рассуждений нередко встречаются ошибки, связанные с ними. Таковыми являются заключения «от отрицания основания условного высказывания к отрицанию следствия», а также «от утверждения следствия к утверждению основания условного высказывания». То есть, неправильны, не гарантируют истинность заключения при истинности посылок такие формы умозаключений:

 

 

Неправильно, например, рассуждать так: «Если число 456 делится на 2 и на 3, то оно делится на 6. Число 456 делится на 6. Следовательно, оно делится на 2 и на 3». Рассуждение здесь, очевидно, идет от утверждения следствия к утверждению основания, то есть неправильно по форме, хотя заключение здесь (в данном конкретном случае), как нетрудно убедиться, является истинным. Но дело в том, что эта истинность заключения не гарантирована истинностью посылок. Умозаключение кажется здесь правильным, потому что известна истинность условного высказывания, обратного данному: «Если число делится на 6, то оно делится на 2 и на 3». Взяв эту посылку вместо данной в нашем примере, мы получим, конечно, правильное умозаключение.

Условно-категорические выводы описанного вида надо отличать – что не всегда делается – от выводов, в которых вместо условной посылки имеется общее суждение субъективно-предикатного типа с условным предикатом (см. § 32). Среди них могут быть выделены две формы, аналогичные двум основным формам условно-категорического силлогизма:

 

 

Пример

 

 

Умозаключения этого типа легко сводятся к рассмотренным – если учесть, что из общих суждений, которые являются их посылками, выводимы условные высказывания. Например, из того, что для всякого проводника верно, что если по нему проходит ток, то он нагревается, выводимо: если по проводнику а проходит ток, то он нагревается. В этом выводе применяется правило, подобное правилу исключения квантора общности в исчислении предикатов (см. § 11). Будем говорить, что это есть правило перехода от общего к единичному случаю этого общего.

 

УСЛОВНО-РАЗДЕЛИТЕЛЬНЫЙ (ЛЕММАТИЧЕСКИЙ) СИЛЛОГИЗМ

Умозаключения этого вида есть выводы из трех и более высказываний, причем две или более посылок – условные высказывания, а одна – дизъюнктивная посылка, которая традиционно называется разделительным суждением. Причем разделительное суждение может быть как со слабой, так и со строгой дизъюнкцией (см. § 30). Мы рассмотрим случай, когда употребляется слабая дизъюнкция, как более общий случай.

В ситуации двух условных высказываний эти силлогизмы называются дилеммами. Причем различают два вида дилемм: конструктивные и деструктивные. Конструктивная (утверждающая) дилемма имеет вид:

 

 

Пример конструктивной дилеммы.

Студент, не готовившийся заранее к экзамену, накануне экзамена оказывается перед дилеммой:

 

 

¹Вероятно, читатель почувствовал, что пример здесь довольно надуманный. И это не случайно, ибо если выводы такого рода и встречаются в практике, то, по-видимому, очень редко. Чаще встречаются формы, когда вместо дизъюнктивной посылки дается конъюнкция, члены которой являются отрицаниями следствий данных условных суждений и заключение в этом случае представляет собой конъюнкцию отрицаний их оснований (антецедентов). Именно эту форму часто принимают за деструктивную дилемму. В нашем случае посылка могла бы быть: «Иванов не получает зарплату и не получает стипендию». А заключением было бы тогда суждение: «Иванов не работает и не учится» хотя допустимо, вообще говоря, и более слабое высказывание: «Иванов не работает или Иванов не учится», ибо р & q ╞ p v q.

 

Однако имеется и третья форма лемматических умозаключений, существование которой обычно не отмечается в учебниках. Это смешанный условно-разделительный силлогизм – конструктивно-деструктивный силлогизм или все равно, что деструктивно-конструктивный. Некоторые из членов разделительной посылки в этих умозаключениях указывают на наличие оснований каких-нибудь из условных суждений, а иные – представляют собой отрицание следствий (консеквентов) условных суждений.

Так, например, конструктивно-деструктивной является дилемма вида:

 

 

Возникает вопрос: возможно ли правильное умозаключение, если, по крайней мере, один член разделительной (дизъюнктивной) посылки отрицает основание или утверждает следствие условных посылок? Ответ на этот вопрос становится очевидным, если учесть возможность сведения лемматических выводов к условно-категорическим. Здесь имеется в виду особый способ рассуждения, так называемое «рассуждение по случаям». Он состоит в том, что при наличии разделительного суждения для осуществления выводов из него в сочетании с какими-то другими суждениями поочередно рассматривается каждый из случаев, на которые указывает разделительное высказывание. В нашем случае, когда с разделительной посылкой мы имеем условные, вывод каждый раз осуществляется по тому или иному правильному модусу условно-категорического силлогизма. Так, имея, например, условные суждения. «Если А, то В»; «Если С, то D»; «Если М, то Ф» и разделительное Аили не-D или М, рассуждаем по случаям:

– положим, истинно А, тогда (по modus ponens) из этого утверждения и первого условного получаем В;

– далее, полагая истинность не-D, выходим (по modus tollens) не-С;

– и, наконец, в предположении, что имеет место М, заключаем, что истинно Ф.

Поскольку рассматриваемую возможности составляют дизъюнкцию, то таким же образом объединяем и следствия, то есть имеем заключение:

«В или не-С или Ф».

Среди дилемм различают еще простые и сложные. Приведенные выше были сложными. Дилемма является сложной, когда как основания, так и следствия условных суждений различны.

В простой дилемме, если она конструктивная, основания различны, а следствие в условных суждениях одно и то же.

В деструктивной же дилемме основание одно и то же, а следствия различны.

 

 

Так, приведенное выше рассуждение относительно нерадивого студента можно преобразовать в простую конструктивную дилемму:

 

 

Условно-разделительные силлогизмы называют лемматическими умозаключениями, имея в виду возможность обобщения дилемм за счет увеличения числа условных высказываний и соответственно – членов разделительного суждения. Так, умозаключение вида:

 

 

называется сложной конструктивной трилеммой.

Читателю должно быть ясно, как можно продолжить обобщения. Однако случаи, когда число условных суждений (высказываний) более трех являются весьма уникальными.

Чисто-условный силлогизм. Это выводы из любого количества посылок, представляющих собой условные высказывания. Наиболее типичны выводы из двух условных высказываний:

 

 

Выводы этого вида характеризуют как выводы на основании транзитивности импликации. Ясно, конечно, что можно иметь сколь угодно длинную цепь транзитивности:

 

 

Разделительно-категорический силлогизм. Это умозаключение из двух или более посылок, в которых, по крайней мере, одна – разделительное суждение. Основными формами являются:

 

 

Понятно, что дизъюнкция (разделительная) посылка может содержать и более двух членов. Однако формы выводов с такими посылками можно сводить к указанным, если учесть, что дизъюнкция ассоциативна и коммутативна (см. § 11), то есть в дизъюнктивном высказывании с более чем двумя членами возможна любая расстановка скобок, а сами члены дизъюнкции можно переставлять в любом порядке, получая при этом высказывания, равносильные исходному. Например, умозаключение вида:

 

 

Вообще, все формы выводов этого вида могут быть сведены к двум общим правилам:

1. Если из всех возможностей, на которые указывает разделительное высказывание, какие-то не имеют места, то имеют место все остальные – обобщение модусаtollendo ponens.

2. Если из исключающих друг друга возможностей, на которые указывает разделительное суждение со строгой дизъюнкцией, какая-то имеет место, то не имеют места остальные – ponendo tollens.

 

Пример

 

Суждение «Риск – благородное дело» (которое, очевидно, является простым) является единичным, или общим, или частным. Но оно не является единичным. Следовательно, это суждение общее или частное.

 

Вместо употребленной здесь посылки со слабой дизъюнкцией можно было бы, очевидно, взять и со строгой, сильной дизъюнкцией, поскольку в действительности члены данной посылки исключают друг друга. Тогда правильным был бы следующий вывод:

 

 

Ко всему сказанному надо добавить, во-первых, что перечисленные формы умозаключений – это, по существу, правила довольно простых умозаключений. Однако умозаключения, как мы уже говорили, могут быть и сложными, представляющими собой последовательности нескольких простых умозаключений, каждое из которых осуществляется по одному правилу. Обратимся, например, к примеру чисто условного силлогизма о студенте, который не занимается систематически. Проницательный читатель мог заметить, что заключение о нем может быть ложным, если имеется в виду, к примеру, студент с выдающимися способностями (который может иметь прочные знания, даже не занимаясь систематически). В чем же, спрашивается, состоит причина того, что в правильном умозаключении заключение оказывается ложным? Для выяснения ее можем построить следующий вывод:

Известно, как мы уже подчеркивали, что если дедуктивное умозаключение правильно и посылки его истинны, то заключение его тоже истинно. В рассмотренном умозаключении заключение неистинно, значит неверно, что оно правильно и посылки его истинны (по модусу tollens условно-категорического силлогизма: если А и В, то С, не-С. Следовательно, не-(А и В)). Но это означает, что это умозаключение неправильно или какая-то из его посылок неистинна (по правилу отрицания конъюнкции). Однако умозаключение правильно. Следовательно, какая-то из посылок этого умозаключения неистинна (Очевидно, таковой является первая – «Если студент занимается не систематически, то он не имеет прочных знаний».) (модус tollendo ponens разделительно-категорического силлогизма: не-А или не-В; А, следовательно, не-В). Заметим, что ради упрощения мы пропустили здесь еще одно звено, а именно: от высказывания «умозаключение правильно» к «значит, неверно, что оно неправильно» (снятие двойного отрицания).

Из этого примера видно уже, что перечисленных в данном параграфе правил недостаточно для того, чтобы в любом случае осуществить вывод из некоторого множества посылок А₁, ..., А_n высказывания В при наличии логического следования А₁, ..., А_n ╞ В. Полную систему правил, позволяющую построить вывод, соответствующий любому отношению логического следования в языке логики высказываний (ЯЛВ), указывают рассмотренные выше натуральные системы исчисления высказываний (см. § 10). А логика высказываний вообще, как и логика предикатов, дает нам также критерии и способы проверки правильности умозаключений из сложных высказываний.

Поскольку задача наша здесь состояла в том, чтобы выделить наиболее типичные, практически важные формы умозаключений, следует добавить к перечисленным две формы выводов – правила так называемых косвенных рассуждений,– которые не были замечены как специальные правила вывода в традиционной логике и получили точные формулировки в рамках символической логики (как правила выводов в логике высказываний – см. § 10). Этими формами нередко пользуются в процессах аргументации (см. § 47), в частности, как средствами доказательств и опровержений. Не случайно сами их названия связаны именно с процессами этого рода. Одна из них – доказательство «от противного», другая – опровержение «путем сведения, к абсурду». Сразу следует заметить, что эти формы вывода, вероятно, известны читателю из школьных курсов математики и геометрии. Однако обычно при употреблении этих способов рассуждения не выявляют структуру этих выводов, в силу чего они не рассматриваются как особые правила рассуждения. Это сделано лишь в рамках логики высказываний.

Рассуждение по первой из этих форм – «от противного» – имеет рассмотренную ниже структуру.

Дано некоторое множество посылок – высказываний – Г и подлежащее доказательству некоторое высказывание А. Рассуждая «от противного», предполагаем, что Аневерно (не-А). Задача теперь состоит в том, чтобы прийти к противоречию, а именно: попытаться из множества высказываний Г и не-А вывести некоторое высказываниеВ и из тех же самых посылок Г и не-А – также не-В. Наличие двух таких выводов позволяет заключить, что если все высказывания, содержащиеся в Г, истинны, то истинно и А («что и требовалось доказать»,– как обычно говорят использующие этот метод). В логике высказываний это правило умозаключения представляется в виде:

 

 

 

Выводимость, стоящая под чертой, дает право считать ложным суждение А при истинности всех высказываний Г.

Таким образом, два известных способа рассуждения структурируются здесь в два точно формулируемые правила рассуждения; одно из них дает возможность доказательства А, другое – опровержения А, то есть доказательства не-А.

Строгое проведение рассуждений этих видов предполагает, что точным образом выделяется множество истинных высказываний (посылок) Г, что в практике рассуждений этого типа отнюдь не всегда делается. Без этого доказательство или опровержение не является строгим и не гарантирует истинность заключительного высказывания А или не-А, поскольку какие-то невыявленные явно посылки могут оказаться ложными.

 

Упражнения

 

1. Используя описанные в данном параграфе формы выводов, решите вопрос, являются ли правильными следующие умозаключения; если – да, то покажите, как оправдать их; если – нет, объясните, почему?

а) Если число рационально, то оно вещественно. Если число натурально, то оно рационально. Значит, если число является натуральным, то оно вещественно.

б) Если прямая касается окружности, то радиус, проведенный в точку касания, перпендикулярен к ней. Таким образом, радиус окружности не перпендикулярен к этой прямой, поскольку она не касается окружности.

в) Потерпевшим признается лицо, которому преступлением нанесен моральный, физический или имущественный вред. Ни моральный, ни физический вред потерпевшему не нанесен. Следовательно, ему нанесен имущественный вред.

г) Если человек является последовательным материалистом, то он признает познаваемость мира. Если человек признает познаваемость мира, то он не является агностиком. Следовательно, если человек не является последовательным материалистом, то он – агностик.

д) Если человек говорит неправду, то он заблуждается или сознательно вводит в заблуждение других. Этот человек говорит неправду, но явно не заблуждается (в этом вопросе). Следовательно, он сознательно вводит в заблуждение других.

е) Если в мире есть справедливость, то злые люди не могут быть счастливы. Если мир есть создание злого гения, то злые люди могут быть счастливы. Значит, если в мире есть справедливость, то мир не может быть созданием злого гения.

ж) Если б он был умен, то он увидел бы свою ошибку. А если б он был искренен, то признался бы в ней. Однако прошлое его поведение показывает, что он или не умен, или неискренен, а может быть и то, и другое. Таким образом, следует ожидать, что он или не увидит ошибку, или не признается в ней.

з) Практика показывает, что если отпечатки пальцев, обнаруженные на месте преступления, не состоят на дактилоскопическом учете, то это существенно затрудняет оперативное расследование преступлений, совершенных особо опасными рецидивистами. В таком случае требуется дополнительное привлечение сотрудников оперативно-розыскного аппарата. Однако в данном случае, думаю, что этого не потребуется, ведь полученные отпечатки пальцев имеются в нашей дактилоскопической картотеке.

2. Сделайте вывод по правилу контрапозиции из суждений:

а) Если слово ставится в начале предложения, то его положено писать с большой буквы.

б) Если слово изменяется по падежам и по числам, то оно является существительным.

в) Дело подлежит передаче в вышестоящий суд, если на приговор подана жалоба или принесен протест.

г) Число 253 не оканчивается на 0 или на 5, значит оно не делится на 5.

 

 Выводы из категорических суждений. Непосредственные умозаключения

Категорические суждения, как мы уже отмечали, являются специфическими формами высказываний (суждений) в естественных языках. Поэтому специфичны и формы выводов из них. При этом имеются в виду именно такие выводы, в которых и посылки, и заключения представляют собой категорические суждения. Выводы этого рода делятся на два вида. В одном случае заключение выводится только из одной посылки – они называются непосредственными. Среди непосредственных, в свою очередь, выделяются умозаключения, основу которых составляют свойства отношений между категорическими суждениями (выводы по логическому квадрату) и выводы посредством преобразования категорических суждений (обращение, превращение и т.д.). Другой вид составляют выводы из двух или большего числа категорических суждений. Это так называемые опосредованные умозаключения. При этом особо выделяются формы умозаключений с двумя посылками. Их называют простыми категорическими силлогизмами, при наличии более чем двух посылок силлогизм называется сложным.

При анализе категорических суждений (см. § 29) было обращено внимание на специфику суждений с пустыми субъектами. Эти суждения, как мы говорили, не имеют реального содержания и поэтому не существует объективно определенных условий истинности этих суждений.

В зависимости от соглашений имеются различные теории того, какие суждения с пустыми субъектами считать истинными и какие ложными (см. § 29). Этими различиями обусловлено и то, что есть некоторые формы выводов, которые считаются правомерными в одних теориях и не считаются таковыми в других. В одной из них – теории оккамовского типа,– считающейся наиболее естественной, допускаются суждения с пустыми субъектами. При этом по соглашению все утвердительные суждения такого типа считаются ложными, а отрицательные, наоборот,– истинными.

В традиционной логике, по существу, исключаются суждения не только с пустыми субъектами, но и с пустыми предикатами и подразумеваются соответственно этому условия относительно всех терминов в суждениях: они не должны быть пустыми, а также и универсальными (как покажем далее, без выполнения этих условий некоторые из описываемых в этой теории форм выводов оказываются неправомерными). Это, конечно, очень сильные ограничения. Желая иметь дело лишь с теми суждениями, которые имеют реальное содержание, достаточно требование лишь не пустоты субъектов и притом лишь, как сказано, в общих суждениях. Мы будем придерживаться здесь именно этой позиции, как наиболее естественной и связанной с минимальными ограничениями допустимых правил вывода. Она естественна, поскольку имеются в виду лишь суждения с реальными содержаниями, и наиболее проста, поскольку обусловливает необходимость различения пустых и непустых терминов и касается это лишь субъектов общих суждений.

ВЫВОДЫ НА ОСНОВЕ СВОЙСТВ ОТНОШЕНИЙ МЕЖДУ КАТЕГОРИЧЕСКИМИ СУЖДЕНИЯМИ (ВЫВОДЫ ПО «ЛОГИЧЕСКОМУ КВАДРАТУ»)

В § 34 были рассмотрены виды отношений между категорическими суждениями. Эти отношения, как мы видели, изображаются с помощью «логического квадрата». Выводы, которые мы здесь рассматриваем, непосредственно обусловливаются свойствами этих отношений.

Так, отношение контрарности (противоположности) – между суждениями видов «Все S суть Р» и «Ни одно S не есть Р», то есть между суждениями типа А и Е с одними и теми же субъектами и предикатами,– характеризуется тем, что эти суждения не могут быть одновременно истинными (верхняя горизонталь квадрата). Значит, если нам дано, что какое-то из этих суждений истинно, то из этого правомерно заключить, что другое ложно, а это, в свою очередь, означает, что истинно его отрицание (здесь как раз существенно предположение, что субъекты суждений – понятие S – не пусто; иначе – суждение не осмысленно, а при выполнении этого условия каждое суждение либо истинно, либо ложно). Таким образом, имеем правила вывода:

 

 

Поскольку мы знаем, что все жидкости упруги (суждение типа А), то можем заключить: «Неверно, что ни одна жидкость не является упругой» 

Субконтрарные суждения типа I и О (нижняя горизонталь), наоборот, не могут быть оба ложными. В силу этого имеем:

 

 

По вертикалям – отношение подчинения – истинность А (подчиняющего суждения) обусловливает истинность I (подчиненного). Ложность же подчиненного (I) влечет ложность подчиняющего; аналогично и для суждении вида Е и О:

 

 

Правила эти, очевидно, тривиальны: если истинно утверждение о всех предметах класса (общие суждения), то истинно, конечно, это утверждать и для любой части этого класса, а то, что ложно для части, ложно и для всего класса. Вместе с тем есть теории – допускающие суждения с пустыми субъектами,– в которых умозаключения этого типа неправомерны, что, очевидно, свидетельствует о неестественности самих таких теорий.

Наконец,– по диагоналям логического квадрата – мы имеем уже хорошо знакомое читателю отношение контрадикторности (противоречия). Контрадикторные сужденияА и О, а также E и I не могут, как мы знаем, быть одновременно истинными, а также и ложными. Это значит, что правильны умозаключения:

 

 

Нетрудно заметить, что если нам известна истинность какого-нибудь из общих суждений (А или Е), то можно сделать заключения о ложности или истинности всех других суждений логического квадрата. Аналогично, ложность какого-нибудь из частных суждений (I или О) детерминирует истинностные значения всех других.

 

Упражнения

 

1. Осуществите все возможные выводы по логическому квадрату из истинности суждения «Любой человек мечтает быть счастливым», а также из ложности суждения «Встречаются студенты, не имеющие среднего образования». (Указание: для выполнения задания данные суждения необходимо представить в стандартной форме – см. § 29).

2. Какие выводы можно сделать из ложности суждений: «Ни один человек не может прыгнуть выше двух метров», «Не найдется человека, знающего более 10 иностранных языков», а также из истинности «Есть люди, бывавшие на Луне»?

3. Определите, являются ли правильными умозаключения:

а) Если неверно, что всякое явление познаваемо, то неверно также, что всякое явление не познаваемо.

б) Из того, что некоторые философы являются агностиками, следует, что некоторые философы не являются таковыми.

в) Поскольку истинно, что некоторые живородящие не являются млекопитающими, следовательно, некоторые млекопитающие животные не являются живородящими.

г) Если неверно, что все преступления умышленны, значит истинным будет противоположное суждение.

 

ВЫВОДЫ ПОСРЕДСТВОМ ПРЕОБРАЗОВАНИЯ СУЖДЕНИЙ

Для понимания сути и значения этих умозаключений надо помнить сказанное ранее о том, что в любом суждении наряду с явно выражаемой в нем информацией содержится еще и некоторая скрытая информация. Это означает, что каждое суждение многосторонне по своему смыслу. Формы выводов, которые предстоит рассмотреть в этом разделе, представляют собой как раз способы выявления того, что в суждении содержится неявным образом.

Например, в утвердительных суждениях «Все S суть Р» и «Некоторые S есть Р» непосредственно (явно) отражается отношение тождества. Первое буквально означает: «Всякий предмет (из некоторого подразумеваемого рода D), обладающий свойством S, тождествен какому-нибудь предмету этого же рода, обладающему свойством Р». Второе суждение утверждает то же самое лишь о некоторых предметах со свойством S. Однако здесь заключена также информация об отношении различия, а именно о том, что ни один предмет из класса D, обладающий свойством S, не тождествен никакому из предметов этого же класса, не имеющему свойства Р. И, наоборот, отношение различия, которое составляет непосредственный смысл отрицательных суждений, связано с отношением тождества. В том, что ни одна кислота не является химически простым веществом (то есть отличается от каждого химически простого вещества), заключена также и информация о том, что каждое вещество, являющееся кислотой, тождественно какому-то из веществ, являющихся не простыми химическими веществами. Эта связь тождества и различия устанавливается при помощи одного из видов непосредственных умозаключений – превращения суждений.

С другой стороны, в любом суждении с субъектом S и предикатом Р непосредственно выражено знание (о тождестве или различий с предикатами Р), относящееся к классу предметов S. При этом либо обо всех предметах класса, либо о некоторых из них. Неявно же в нем содержится знание (об отношениях тех же типов) относительно предметов класса Р. «Скрытая» информация этого рода выявляется в непосредственных выводах, называемых обращением суждений.

Существенную роль в этих, как и в опосредованных, выводах из категорических суждений, играет понятие распределенности терминов. Распределенность или нераспределенность субъекта или предиката в некотором суждении означает как раз то, имеем ли мы в этом суждении информацию соответственно обо всех или не обо всех предметах соответствующего класса (S и Р).

На распределенность или нераспределенность субъекта указывает, очевидно, количественная характеристика суждения («Всякий» или «Некоторый»), Что касается объема информации относительно предиката, то он зависит от качества суждения. В утвердительных суждениях мы не имеем полной информации о предметах Р,поскольку в них утверждается тождество (всех или некоторых) предметов с какими-то предметами Р. Это означает, что в таких суждениях предикат» нераспределен.

В отрицательных же суждениях предикат распределен, ибо в них мы имеем знание о том, что все или некоторые предметы не тождественны ни с одним предметом Р.

• Итак, мы имеем следующие правила распределенность терминов в категорических суждениях.

1. Субъекты распределены в общих и не распределены в частных суждениях.

2. Предикаты распределены в отрицательных и не распределены в утвердительных суждениях.

Читателю важно хорошо усвоить, что приведенные смысловые характеристики суждений определяются исключительно лишь их формами (структурами). Важно правильно различать, что именно мы можем извлечь из данного суждения, от всех других имеющихся у нас знаний. Кажется, например, что в суждении «Некоторые музыканты – композиторы» заключено знание и о том, что «Все композиторы – музыканты». Однако такая иллюзия возникает в силу того, что это знание мы имеем дополнительно, независимо от данного суждения. В нем содержится (неявно) информация лишь о том, что некоторые композиторы – музыканты.

Превращение и обращение категорических суждений представляют собой основные формы выводов посредством преобразования суждений. Наряду с ними имеются и некоторые производные выводы – те или иные сочетания указанных.

ПРЕВРАЩЕНИЕ

Это вывод, в котором заключение получается посредством эквивалентного преобразования утвердительного суждения в отрицательное и наоборот. Эквивалентность достигается за счет того, что при изменении качества суждения изменяется также его предикат – он заменяется противоречащим понятием (В упомянутой выше теории оккамовского типа допустимы лишь превращения утвердительных суждений в отрицательные. И потому вообще данная операция не представляет собой эквивалентное преобразование высказываний.).

Рассмотрим формы таких выводов для всех видов категорических суждений.

 

 

В силу эквивалентности преобразования справедливы выводы и в обратную сторону – от нижнего суждения к верхнему.

 

Примеры

 

1. Все жидкости упруги. Следовательно, ни одна жидкость не есть неупругое вещество.

2. Ни одно суворовское сражение не было проиграно. Следовательно, все суворовские сражения суть непроигранные сражения.

3. Некоторые озера имеют сток. Следовательно, некоторые озера не есть водоемы, не имеющие стока.

4. Некоторые философы не являются атеистами. Следовательно, некоторые философы суть не атеисты.

При разборе этих примеров читателю предлагается вспомнить сказанное ранее о структурах категорических суждений и о стандартных формах их представления. Без этого непонятно, почему, например, в качестве предиката заключения в первом примере появилось «неупругое вещество», а в третьем – «водоем, не имеющий стока». При стандартизации этих выводов первое из приведенных умозаключений должно выглядеть так:

Все вещества, которые являются жидкими, суть упругие вещества. Следовательно, ни одно вещество, которое является жидким, не есть неупругое вещество.

Без такой стандартизации могут возникнуть нелепости вроде следующей:

Всякое кристаллическое вещество плавится при определенной температуре. Следовательно, ни одно кристаллическое вещество не есть не плавится при определенной температуре.

Правильным заключение должно быть, конечно:

Ни одно кристаллическое вещество не есть вещество, которое не плавится при определенной температуре.

При стандартизации суждений важно иметь в виду, что субъект и предикат категорического суждения должны иметь один и тот же род. Стандартизация посылок и заключений избавит читателя от возможных трудностей не только в превращениях, но и в других рассматриваемых далее операциях с категорическими суждениями.

 

ОБРАЩЕНИЕ

Обращение – это умозаключение, при котором из данного суждения, не являющегося частноотрицательным, выводится такое, субъектом которого является предикат исходного, а предикатом – субъект исходного. При этом в случае, когда исходное суждение – посылка – является общеутвердительным, меняется также само суждение, а именно: заключение представляет собой частное суждение. Этот случай обращения называется «обращением с ограничением», а в других случаях – «чистым ограничением». Итак, имеем три основных формы обращения:

1. Обращение общеутвердительного суждения

 

 

«Всякий студент обязан сдавать какие-нибудь экзамены. Следовательно, некоторые люди, обязанные сдавать какие-нибудь экзамены, суть студенты».

2. Для общеотрицательного суждения

 

 

но при условии непустоты Р, то есть при условии, что полученное суждение является осмысленным – имеет реальное содержание.

 

Примеры

 

Ни одна из рыб не является теплокровным животным. Следовательно, ни одно теплокровное животное не есть рыба.

Ни один человек не желает иметь врагов. Следовательно, ни один желающий иметь врагов не есть человек... Стоп!? Получается какая-то нелепость. В чем причина? Дело в том, что здесь не выполнено сформулированное выше требование о стандартизации и о том, что субъект и предикат должны иметь общий род. Правильным результатом обращения в данном примере будет:

Ни одно существо, желающее иметь врагов, не есть существо, являющееся человеком.

Однако из суждения «Ни один человек не может жить без пищи» неправомерно выводить «Ни одно существо, которое может жить без пищи, не есть человек», поскольку таких существ вообще не существует (Покажем, как неограничение применения правил обращения в совокупности с правилами превращения может приводить к ложным результатам при истинных посылках. Известно, например, что математики, а также и нематематики до возникновения геометрии Лобачевского пытались доказать 5-й постулат Эвклида. С появлением геометрии Лобачевского стало ясно, что невозможно как доказательство, так и опровержение 5-го постулата Эвклида в эвклидовой геометрии. Возьмем теперь истинное суждение «Ни один математик не доказал 5-й постулат Эвклида». Обращая его, получим «Ни один человек, доказавший 5-й постулат, не есть математик». Превращая его, имеем «Все люди, доказавшие 5-й постулат, суть не математики» и, обращая его, получим: «Некоторые не математики доказали 5-й постулат Эвклида», что явно ложно. В традиционной теории мы вообще не имеем права использовать исходное суждение, поскольку в нем один из терминов – предикат – является пустым. Однако оно вполне осмысленно и, более того, в науке очень часто отрицательные суждения имеют пустые предикаты. Хуже того, согласно ограничениям традиционной логики, нельзя использовать даже такое, например, суждение, как «Всякий человек нуждается в пище» (то есть является существом, которое нуждается в пище), поскольку понятие – предикат «существо, нуждающееся в пище» – является универсальным (а это значит, что при превращении данного суждения получится суждение с пустым предикатом). Отсюда ясно, насколько жесткими являются ограничения, которые подразумеваются в традиционной логике, а без этих ограничений эта теория является некорректной.).

3. Суждение частноутвердительное обращается

 

 

Некоторые простые числа являются четными. Следовательно, некоторые четные числа суть простые числа.

Пояснение. Пусть читателя не удивляет, что мы здесь говорим о «некоторых» простых числах, являющихся четными, в то время, как есть только одно такое число (а именно – число 2). Такое словоупотребление логически правомерно, поскольку «некоторые» означает: «по крайней мере одно, а может быть и все». Вообще, частное суждение «Некоторые S суть Р» или «Некоторые S не суть Р», по существу, просто указывает на существование среди предметов общего рода для S и Р таких предметов, которые одновременно обладают свойствами S и Р или таких, которые, обладая свойством S, не имеют свойства Р. Из частноотрицательного суждения путем обращения нельзя логически правильно вывести какое-либо заключение. Это будет ясно, если учесть общее правило обращения, как и выводов из категорических суждений вообще:термин, не распределенный в посылках, не должен быть распределен в заключении.

Если бы мы попытались обратить частноотрицательное суждение, то оказалось бы, что термин S, не распределенный (как субъект частного суждения) в посылке, оказался бы распределенным (как предикат отрицательного суждения) в заключении. В силу этого же правила обращение общеутвердительного суждения осуществляется с ограничением. Иначе термин Р, не распределенный в посылке, оказался бы распределенным в заключении.

Нарушение указанного правила означало бы, что в заключении получается дополнительная или более широкая информация по сравнению с той, которая содержится в посылках. Приращение же информации в правильных дедуктивных выводах невозможно. Попутно заметим, что это часто трактуют неправильно в виде тезиса: «Дедуктивное умозаключение не дает нового знания по сравнению с посылками». При этом не различают знание и информацию. Информация, неявно содержащаяся в посылках, не есть знание. Она становится знанием, когда извлекается из посылок и фиксируется в форме высказывания. Это и осуществляется в дедуктивных умозаключениях. Правильные дедуктивные умозаключения представляют собой как раз способы правильного извлечения информации из той или иной совокупности высказываний. И они, вопреки приведенному ошибочному тезису, являются важным средством приращения знания в процессе познания. К этому надо добавить, что информация сама по себе может быть истинной и ложной, именно поэтому заключение даже правильного дедуктивного умозаключения может быть ложным. Это возможно (но не обязательно), когда по крайней мере одна из посылок дедуктивного вывода ложна. Знание же по своему понятию есть та информация, которая выражается в истинном высказывании.

Замечание. Иногда различают сильные и слабые превращения и обращения, имея в виду, что, например, из суждения «Все S суть Р» наряду с выводом – посредством превращения – суждения «Ни одно S не есть не-Р» можно вывести также «Некоторые S не есть не-Р». Из суждения «Ни одно S не есть Р» путем обращения можно вывести не только «Ни одно Р не есть S», но также и «Некоторые Р не есть S».

Таким образом, второй вариант («слабое превращение» и «слабое обращение») дает более слабое заключение, чем первый. Однако слабые превращения и обращения представляют собой просто сложные выводы. Заключение каждого из них получается в два шага:

1. Обычное («сильное») обращение или превращение.

2. Вывод из полученного суждения более слабого – частного – заключения по правилу логического квадрата – от подчиняющего суждения к подчиненному (вертикали логического квадрата).

Возможны сложные выводы и по правилам преобразования категорических суждений. Среди них особо выделяют противопоставление предикату и противопоставление субъекту.

Первый вывод является последовательным применением превращения исходного суждения и далее обращения полученного при этом суждения.

Второй также представляет собой последовательное применение тех же операций, но в обратном порядке: сначала осуществляется обращение исходного суждения, а затем – превращение полученного результата.

Так. противопоставление предикату суждения вида «Все S суть Р» представляет собой вывод:

1. «Все S суть Р» – посылка.

2. «Ни одно S не суть не-Р» – по правилу превращения из 1.

3. «Ни одно не-Р не есть S» – по правилу обращения из 2. Противопоставление субъекту суждения того же вида будет выглядеть так:

1. «Все S суть Р» – посылка.

2. «Некоторые Р суть S» – по правилу обращения из 1.

3. «Некоторые Р не суть не-S» – по правилу превращения из 2.

Для остальных видов категорических суждений выводы данного типа – когда они возможны – предлагается осуществить читателю самостоятельно. Надеемся, что при этом будет обнаружено, что нельзя осуществить противопоставление предикату частноутвердительного суждения и противопоставление субъекту частноотрицательного.

В разделах исчисления высказываний и предикатов (§§ 10, 11) мы видели, что для любого сложного вывода можно сформулировать результирующее правило вывода заключения из соответствующих посылок. В нашем случае таковыми будут следующие правила:

 

ПРОТИВОПОСТАВЛЕНИЕ ПРЕДИКАТУ

ПРОТИВОПОСТАВЛЕНИЕ СУБЪЕКТУ

 

Пример

 

Из суждения «Все лгуны – малодушные люди» по правилу противопоставления предикату получаем: «Ни один немалодушный человек не является лгуном».

Не кажется ли Вам, что заключение данного умозаключения является ложным? Это действительно так, ибо и немалодушный человек может лгать ради каких-то своих особых целей. Поскольку же само умозаключение здесь логически правильно, то ложность его заключения указывает на ложность посылки. А между тем сама по себе она не производит впечатление ложной (хотя и является такой). Здесь мы имеем возможность отметить еще одну функцию правильных дедуктивных умозаключений. Наряду с тем, что эти формы умозаключений являются средством получения нового знания, они в ряде случаев могут служить также способом проверки истинности высказываний.

По правилу противопоставления субъекту из высказывания «Ни один любящий себя человек не желает себе зла» получаем «Всякий человек, желающий себе зла, есть человек, не любящий себя».

 

Упражнения

 

1. Осуществите выводы посредством превращения, обращения, противопоставления субъекту и предикату:

а) Никакой из законов логики не является результатом соглашения;

б) Все народы желают мира.

2. Укажите, какие выводы можно осуществить – и осуществите их – из следующих высказываний посредством приведенных выше форм преобразования категорических высказываний:

а) Многие люди, вошедшие в историю как великие личности, были тиранами;

б) Некоторые люди, прославившиеся после смерти, не были замечены своими современниками как выдающиеся личности.

3. Осуществите вывод, последовательно применяя превращение, обращение и снова превращение, из высказываний:

а) Ни один нерадивый студент не может достичь хороших успехов в учебе;

б) Все криминальные ситуации, которыми занимался Шерлок Холмс, были такими, раскрытие которых было доступно не каждому сыщику.

4. Определите форму и правильность непосредственных умозаключений:

а) Истинно, что всякое рациональное число является вещественным. Значит ложно, что любое вещественное число не рационально;

б) Если верно, что некоторые идеалисты являются атеистами, то верно, что атеисты не принадлежат к людям, которые не разделяют идеалистического мировоззрения;

в) Истинно, что некоторые живородящие животные не являются млекопитающими, следовательно, истинно, что некоторые млекопитающие животные не являются живородящими;

г) Иные из категорических суждений можно отнести к частным суждениям, значит, все частные суждения являются категорическими;

д) Так как некоторые естествоиспытатели придерживаются материалистических позиций, то некоторых людей, не являющихся материалистами, нельзя отнести к естествоиспытателям.

 

Выводы из категорических суждений. Простой категорический силлогизм

Простой категорический силлогизм – это вывод некоторого категорического суждения из двух других категорических суждений. Существенно при этом для данного вывода наличие в посылках некоторого одного и того же термина (понятия), называемого средним термином силлогизма, через посредство которого выявляется связь между теми терминами (понятиями), которые составляют субъект и предикат заключения. Таким образом, это опосредованное умозаключение, то есть умозаключение, в котором связь между двумя понятиями (в заключении) устанавливается посредством третьего, имеющегося в обеих посылках. Например:

 

 

Теория умозаключения этого рода была первой в истории логики теорией умозаключений. Она разработана Аристотелем и составляет содержание одной из книг «Органона» – I книги 1-й Аналитики (Аристотель. Соч.: В 4 т.– 1978.– Т. 2.). С возникновением символической логики появилось представление о том, что эти выводы являются частными случаями выводов исчисления предикатов. Однако это мнение оказалось неверным. Как мы уже говорили, выводы из категорических суждений, в том числе и категорический силлогизм, являются специфическими формами умозаключений в естественном языке. Специфичность их обусловлена хотя бы тем, что в обычных формализованных языках логики, в частности, в языке логики предикатов, нет понятий вообще, тогда как они являются составными частями категорических суждений.

Состав категорического силлогизма. Здесь мы должны ввести ряд понятий, которые читателю необходимо усвоить для понимания дальнейшего изложения.

Итак,– что ясно из определения: в простом категорическом силлогизме имеется две посылки и заключение. В посылках имеются три термина – понятия (В нормальных случаях это три попарно различных термина. Но есть некоторые вырожденные случаи силлогизма, в которых какие-то из этих терминов совпадают. Например, меньший термин может совпадать со средним термином.). Два из них входят в состав заключения – крайние термины силлогизма. Одно понятие имеется в составе обеих посылок, но не входит в заключение – средний термин силлогизма. Среди крайних терминов различают меньший термин – субъект заключения, и больший термин – предикат заключения. Соответственно различают и посылки – большую и меньшую. Большая посылка – та, в состав которой входит больший термин; меньшая – та, что содержит меньший термин.

В приведенном примере имеем термины (понятия): «непосредственное умозаключение», «умозаключение с одной посылкой», «простой категорический силлогизм». Крайними терминами являются первый и третий. Первый – больший термин, третий – меньший. Второй – в данном перечислении – средний термин силлогизма. Большей посылкой является первая, меньшей – вторая (порядок посылок, как должен понять читатель, в умозаключениях не играет роли, хотя обычно, при стандартных записях умозаключений категорического силлогизма, в качестве первой посылки ставят большую, в качестве второй – меньшую посылку).

Фигуры силллогизма. Имеются различия в построении силлогических выводов, связанные с положением среднего термина. Эти разновидности называются фигурами силлогизма. Имеются четыре фигуры.

ПЕРВАЯ ФИГУРА. Средний термин играет в ней роль субъекта в большей посылке и предиката в меньшей. Если обозначить соответственно меньший, средний и больший термин посредством знаков S, М и Р, то схематически эта фигура выглядит так:

 

 

Приведенный выше пример относится как раз к фигуре этого типа.

ВТОРАЯ ФИГУРА. В ней средний термин играет роль предиката в обеих посылках. Схематически:

 

 

Первая фигура простого категорического силлогизма используется в процессе познания как способ распространения некоторого общего знания (выраженного в большей посылке) на некоторые особые случаи (класс предметов S). В связи с этим ее характеризуют как способ подведения класса S под М, относительно которого имеется общее знание.

Вторая фигура используется, в основном, как средство опровержения некоторых неправильных подведений чего-либо под некоторое понятие. Пример, который приведен, может рассматриваться как пример опровержения того, что воск является жидкостью.

Третья фигура может применяться в качестве способа опровержения необоснованных обобщений. В приведенном примере – опровержение утверждения «Ни одно водное животное не является млекопитающим».

Четвертая фигура представляет собой искусственное построение и не имеет никаких определенных познавательных функций.

Модусы простого категорического силлогизма. Модусы – это разновидности силлогизма внутри каждой фигуры, различающиеся характером суждений,– посылок и заключения,– составляющих силлогизм. Учитывая наличие четырех типов категорических суждений, можно подсчитать, что в каждой фигуре имеется 64 модуса, а всего – 256. Однако не все они, конечно, представляют собой правильные умозаключения. Таких – правильных модусов – всего лишь 24 (по 6 модусов в каждой фигуре). Среди них выделяется 19 основных, так называемых сильных модусов. Остальные – слабые модусы – могут быть представлены как сложные выводы: сочетания выводов в форме категорического силлогизма с выводами по правилам логического квадрата.

Теория силлогизма в традиционной логике была разработана настолько детально, что все правильные модусы получили специальные названия, которые при этом составлены так, что содержат, в частности, информацию о характере составляющих данный модус суждений.

Так, сильные модусы первой фигуры носят названия: Barbara, Celarent, Darii, Ferio (а слабые: Barbari, Celaront).

Гласные буквы в них указывают на типы суждений, играющих соответственно роль большей посылки, меньшей посылки и заключения. Например, Ferio указывает, что большая посылка – суждение типа Е (общеотрицательное), меньшая – типа I (частноутвердительное), заключение – типа О (частноотрицательное).

Основные правильные модусы второй фигуры: Cesare, Camestres, Festino, Baroko. (Слабые модусы: Cesaro, Camestros.)

В третьей фигуре имеем: Darapti, Disamis, Datisi, Felapton, Bokardo, Ferison.

И, наконец, модусы четвертой фигуры: Bramantip, Camenes, Dimaris, Fesapo, Fresison. (Слабый модус – Camenos.) Однако, учитывая неосмысленность общих суждений с пустым субъектом, надо иметь в виду, что Camenes в четвертой фигуре правилен только при непустом S.

Круговые схемы категорических суждений как средство проверки правильности умозаключении категорического силлогизма и отбора правильных модусов. Указанные выше способы изображения смыслов категорических высказываний (см. § 29) могут служить средством проверки правильности выводов из категорических суждений, а тем самым и способом отбора упомянутых выше правильных модусов в пределах различных фигур, а также и средством решения вопроса о том, какое заключение (следствие) можно правильно вывести из некоторых данных категорических высказываний. Наиболее важное является третий тип задач, поскольку умение решать задачи этого типа является достаточным условием для решения и других задач указанных типов. Но чаще всего ее решение сводится как раз к решению задач других двух типов. Кстати, вспомните, что согласно понятию логического следования, следствием из некоторого множества посылок является, в частности, каждая из посылок этого множества, а также следствия отдельных его посылок (Кроме того, не забывайте, что отношение следствия не зависит от конкретных суждений, а тем самым и от их истинностных значений. Учитывая это, в качестве примеров и задач предлагаются иногда не сами высказывания, а их логические формы.), но нас здесь интересуют не все возможные следствия, а лишь те, в которых выражаются связи между крайними терминами, опосредованные средним термином.

Для того, чтобы решить вопрос, какие следствия относительно связи крайних терминов выводимы из двух посылок категорического типа со средним термином с помощью круговых схем, вообще говоря, надо:

1) составить круговые схемы для каждого из данных суждений;

2) объединить их в одну схему;

3) рассматривая возможно различные варианты связи относительно крайних терминов (S и Р), посмотреть, есть ли такие отношения между ними, которые обязательно имеют место, то есть детерминированы данными посылками. Все суждения, которые соответствуют детерминированным отношениям, и будут искомыми следствиями. Если же между крайними терминами нет отношений, детерминированных посылками, то нет и следствий интересующего нас вида.

Во многих случаях искомые следствия очевидны даже без особого анализа. Если даны, например, высказывания вида «Все S суть М» и «Ни одно М не суть Р», то их схемы

 

 

из которой сразу видно, что данные посылки детерминируют отношение внеположенности (несовместимости) между S и Р и, значит, принуждают нас принять утверждения (вывести следствия): «Ни одно S не есть Р» и «Ни одно Р не есть S» (хотя последнее, как мы уже знаем, является непосредственным следствием из первого – см. «Обращение»).

В иных случаях требуется, по крайней мере, перебор вариантов объединенных схем, допустимых посылками. Например, для выявления следствий из посылок вида «Все М суть Р» и «Все М суть S» надо учитывать возможности, по крайней мере, таких вариантов:

 

 

Первый из этих вариантов наводит на мысль, что «Все S суть Р», второй, что «Все Р суть S», но каждый из них опровергает друг друга, а третий – оба из них. Остаются лишь возможности: «Некоторые S суть Р» и «Некоторые Р суть S». Легко показать, что никакие другие возможности не опровергают этого и не дают ничего нового.

Поскольку при таких переборах возможностей мы выдвигаем некоторые гипотезы типа «верно ли, что "Все S суть Р"» или «Ни одно S не есть Р» и т. д. задача сводится к другой, а именно, к решению вопроса о том, следует ли некоторое высказывание из посылок, то есть правильно ли некоторое умозаключение? Здесь удобен метод рассуждения «от противного»; предполагаем, что заключение ложно при истинности посылок, и смотрим, возможна ли схема контрадикторно-противоположного (противоречащего) высказывания. Бели она невозможна, значит, умозаключение правильно (его заключение действительно детерминировано посылками). В противном случае – нет. Этим методом возможен, собственно, и отбор правильных модусов.

Спрашивается, например, следует ли из посылок видов: «Некоторые S не есть М» и «Все М суть Р» суждение вида «Некоторые S не есть Р»? При этом опять-таки нужно перебрать варианты объединенных круговых схем:

 

 

Противоречащим (контрадикторно-противоположным) для заключения является, очевидно, суждение «Все S суть Р» и надо решить вопрос, возможно ли соответствующее ему отношение? Как видим, оно возможно, что видно из второго варианта объединенной схемы. Значит, решение вопроса о следовании является здесь отрицательным: умозаключение неправильно.

Проверим, следует ли из посылок «Ни одно Р не есть М» и «Некоторые М есть S» суждение «Некоторые S не есть Р». Контрадикторно-противоположным (противоречащим) этому суждению будет «Все S суть Р». Попробуйте построить круговую схему, удовлетворяющую посылкам и содержащую отношение, соответствующее этому высказыванию. Убедитесь, что это невозможно! Это будет означать, что умозаключение правильное.

Можно поступить иначе: взять высказывание, противоречащее заключению, в качестве посылки вместо одной из данных и посмотреть, получается ли из него в сочетании с другой данной посылкой заключение, противоречащее исключенной посылке. Если получается, то значит, исходное умозаключение правильно (Этот способ называют Методом построения антилогизмов. Здесь мы используем законы логики высказываний: если ).

Рассуждая «от противного», в нашем примере возьмем суждение, противоречащее заключению, «Все S суть Р» вместо первой из данных посылок (то есть вместо «Ни одно Р не есть М»). Тогда из него («Все S суть P») и второй посылки «Некоторые М есть S» следует высказывание «Некоторые Р есть М», которое противоречит исключенной (первой) посылке:

 

 

Значит, предположение «от противного» неверно, а проверяемое умозаключение правильно.

Очевидно, что именно подобными способами первоначально осуществлялся отбор правильных модусов, а также устанавливались и другие критерии правильности выводов из категорических суждений, к рассмотрению которых мы теперь и перейдем.

 

Упражнения

 

1. Используя круговые схемы, проверьте правильность модусов: Barbara, Celaront, Baroko, Ferison, Bramantip, Dimaris, Camenos.

2. Покажите неправильность модусов:

A I A, E I E – по первой фигуре;

A A A – по второй фигуре;

A A A – по третьей фигуре;

А А О – по четвертой фигуре.

3. Используя круговые схемы, проверьте различными способами правильность умозаключений:

а) Все люди, достигшие больших успехов в жизни, являются трудолюбивыми. Многие способные люди не являются трудолюбивыми. Следовательно, некоторые способные люди не достигнут больших успехов в жизни;

б) Все честные люди – объективны. Некоторые добрые люди – нечестны. Значит, некоторые добрые люди – не объективны.

 

ОБЩИЕ ПРАВИЛА ПРОСТОГО КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА И СПЕЦИАЛЬНЫЕ ПРАВИЛА ФИГУР КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА

Основная цель изучения разделов темы «Умозаключение» состоит, очевидно, в том, чтобы приобрести определенные навыки построения правильного умозаключения. Для достижения этой цели надо уметь выделять правильные формы умозаключений, отличать правильные от неправильных.

Что касается рассматриваемых здесь форм выводов, то само по себе знание того, какие именно формы являются правильными, очевидно, не достаточно и даже, отнюдь, не суть главное. Важнее знать критерии, условия правильности умозаключений. Такие критерии дают общие правила категорического силлогизма.

Эти правила таковы, что каждое из них является необходимым условием, а все вместе они являются достаточным условием правильности вывода. Причем последнее справедливо с учетом условия относительно осмысленности общих суждений. А именно, требования непустоты их субъектов. Это добавление затрагивает лишь один – уже упоминавшийся – модус силлогизма: Camenes четвертой фигуры.

Вспомните, что означают достаточные и необходимые условия (31). В данном случае необходимость каждого правила означает, что если оно не выполняется в некотором умозаключении, то умозаключение неправильно. Достаточность же всех общих правил выражается в том, что выполнение каждого из них свидетельствует о правильности умозаключения. Иными словами силлогизм правильный, если выполнены все правила простого категорического силлогизма, и силлогизм неправилен, если не выполнено хотя бы одно из них. Учитывая сказанное, эти правила можно характеризовать не только как критерии, но и как определенные требования к умозаключениям этого типа, выполнение которых гарантирует получение истины из истины. Имеется пять таких правил, два из них относятся к терминам, а три других касаются посылок и заключения.

Первое правило. Средний термин должен быть распределен хотя бы в одной из посылок.

Второе правило. Если термин не распределен в посылке, то он не должен быть распределен в заключении.

Третье правило. По крайней мере одна посылка должна быть утвердительной (из двух отрицательных не может быть правильного вывода).

Четвертое правило. Если одна посылка отрицательная, то заключение должно быть отрицательным.

Пятое правило. Если обе посылки утвердительные, то заключение должно быть утвердительным.

Наряду с основными полезно иметь в виду два производных – выводимых из основных – правила:

Шестое правило. По крайней мере, одна из посылок силлогизма должна быть общим суждением (из двух частных заключение не следует).

Седьмое правило. Если одна из посылок частное суждение, то и заключение частное.

Покажем для примера, каким образом может быть обосновано первое из этих правил с использованием основных. По методу от противного предположим, что обе посылки силлогизма частные. Но в них хотя бы один термин – а именно, средний – должен быть распределен (первое правило) это значит, что хотя бы одна из посылок должна быть отрицательной, но тогда и заключение должно быть отрицательным (четвертое правило), в котором будет распределенным предикат. Значит, он и в посылке должен быть распределен (второе правило), а это означает, что и вторая посылка должна быть отрицательной. Однако это невозможно (третье правило).

Имея в виду это доказанное правило, можно сразу усмотреть неправильность следующего силлогистического умозаключения:

 

 

Неправильность этого силлогизма можно установить, конечно, и по общим правилам, а именно: оказывается, что ни в одной из посылок не распределен средний термин (в большей – как субъект частного суждения, в меньшей – как предикат утвердительного).

Мы апеллировали здесь к правилам силлогизма, исходя из того, что данное умозаключение действительно представляет собой такую форму вывода. Однако не всякое умозаключение, в котором две посылки и заключение есть категорические суждения, представляет собой категорический силлогизм. Поэтому прежде чем приступать к анализу того, правильно или неправильно умозаключение с точки зрения правил силлогизма, надо убедиться в том, что данное умозаключение представляет собой именно категорический силлогизм. Для этого недостаточно учитывать только то, что оно состоит из категорических суждений, ибо существуют правильные выводы из двух категорических суждений третьего – того же типа,– которые не представляют собой категорического силлогизма. Например:

 

 

Было бы опрометчивым утверждение о том, что это умозаключение неправильно, поскольку в нем обе посылки отрицательные. Это умозаключение правильно, но оно не является категорическим силлогизмом, поскольку в нем содержится четыре термина: «человек, не имеющий среднего образования», «человек, имеющий аттестат зрелости», «человек, не имеющий аттестата зрелости», «человек, принимаемый в ВУЗ». Хотя, между тем, оно может быть приведено к форме категорического силлогизма и таким образом оправдано. Надо лишь осуществить превращение первой посылки, взяв вместо нее: «Всякий человек, не имеющий среднего образования, есть человек, не имеющий аттестата зрелости». Получим первую фигуру, где большая посылка является, очевидно, второй (Подобные преобразования невозможны в упомянутых выше системах оккамовского типа, где не допускается превращение отрицательных суждений в утвердительные, что указывает на серьезный недостаток этих систем.).

Педагогическая практика показывает, что начинающий изучать логику нередко затрудняется извлечь из данных определений метод анализа силлогистических умозаключений для установления того, являются ли они правильными или неправильными. Поэтому считаем нелишним и практически полезным предложить следующую процедуру анализа.

Прежде всего надо, конечно, убедиться, что данное умозаключение относится к категорическому силлогизму. Для этого необходимо выделить посылки и заключение и представить их в стандартной форме. Не осуществив последнего, мы не можем даже установить, какие термины и сколько их имеется в данном умозаключении. Удобно, но не обязательно, представить само умозаключение в стандартной форме: над чертой – посылки, под чертой – заключение. Положим, что нам дан действительно категорический силлогизм.

1) обозначаем субъект заключения символом S и находим меньшую посылку, фиксируя в ней меньший термин;

2) обозначаем предикат заключения символом Р и находим общую посылку, отмечая в ней больший термин;

3) находим в посылках средний термин и обозначаем его символом М;

4) слева от каждого суждения, входящего в силлогизм, указываем его тип (А, Е, I или О) и распределенность терминов в нем, обозначая распределенность термина знаком « + », а нераспределенность – знаком «–»;

5) наконец, проверяем, удовлетворяет ли умозаключение всем общим правилам силлогизма.

Приведем пример предложенного анализа. Рассмотрим умозаключение:

Частное знание о том, что существует, по крайней мере, один прямоугольник, не являющийся ромбом, вытекает из общего знания о том, что все квадраты суть ромбы и из очевидности того факта, что некоторые прямоугольники не являются квадратами.

Очевидно, что заключением этого умозаключения является первое из приведенных суждений. Два других – его посылками. В стандартной форме – после выполнения процедур 1-5 – умозаключение выглядит так:

 

 

Очевидно, что данный силлогизм неправилен, так как в нем термин (Р), не распределенный в посылке, распределен в заключении, что запрещает второе правило.

Читателя может смутить тот факт, что в данном умозаключении посылки истинны, заключение тоже истинно, а силлогизм – неправильный! Напомним, что в правильных умозаключениях при истинности посылок гарантируется истинность заключения. В неправильных же такой гарантии нет. Это не означает, что при истинности посылок заключение в них обязательно будет ложным. Оно может быть и истинным, но истинность его не обусловлена логической формой умозаключения с истинными посылками. Так, следующее умозаключение, имеющее ту же логическую форму и истинные посылки, дает уже явно ложное заключение:

 

 

Обычно к умозаключениям категорического силлогизма относят умозаключения, в которых используются единичные суждения, рассматриваемые при этом как общие (Строго говоря, единичные суждения вида «а есть Р» не являются категорическими, поскольку категорические определяются как суждения, содержащие лишь общие термины, то есть понятия, причем общие не по количеству предметов, а по самой логической форме: xS(x), xP(x). Однако умозаключения такого рода вполне естественны и могут быть даже оправданы посредством тривиального представления единичного имени как понятия х(х = а), общего по своей форме, где область значений х – областьD – та же, что и для понятиях хР(х). Таким образом, вместо единичного получаем общее суждение: «Всякий х, такой, что х равен а, есть такой предмет х, который обладает свойством Р». Очевидно, оно эквивалентно исходному единичному суждению. Ясно должно быть и то, что употребление слова «всякий» здесь чисто формально, поскольку, согласно свойству отношения равенства, понятие х(х = а) является единичным по своему объему. Однако используя его в данном случае, мы отвлекаемся от количественных характеристик его объема. И важно именно то, что суждение приобретает форму общего категорического суждения. Имея в виду такую возможность сведения единичных суждений к общим, вполне правомерно использовать их в силлогизмах на правах общих суждений, не прибегая каждый раз к указанному преобразованию. Но при этом учитывать, что для такого общего термина S «Все S суть Р» эквивалентно «Некоторые S суть P».):

 

 

Итак, мы имеем критерии для оценки силлогистических выводов как правильных или неправильных. Среди условий правильности силлогизма есть, как мы видели, необходимые и достаточные. Необходимыми условиями являются каждое из общих основных и производных правил. К их числу относятся и следующие специальные правила фигур, которые тоже являются производными – выводимыми из основных.

 

СПЕЦИАЛЬНЫЕ ПРАВИЛА ФИГУР

В первой фигуре:

1. Большая посылка должна быть общим суждением.

2. Меньшая посылка должна быть утвердительным суждением.

Это очевидно уже из самой характеристики первой фигуры. Однако эти правила, как и правила остальных фигур, могут быть получены строго логически, как следствия из основных общих правил.

В правильных выводах по второй фигуре:

1. Большая посылка также является общим суждением.

2. Какая-нибудь из посылок – отрицательное суждение.

В третьей фигуре:

1. Меньшая посылка должна быть утвердительной.

2. Одна из посылок – общее суждение.

3. Заключение – всегда частное суждение.

Для четвертой фигуры, в силу ее искусственности, не удается сформулировать достаточно обобщающие правила; предпринимавшиеся в истории логики попытки указать таковые не увенчались успехом: имеется перечень из четырех правил, перечисление которых, по существу, равносильно перечислению правильных модусов этой фигуры.

 

Упражнения

 

1. Дайте анализ силлогизмов (определите состав, фигуру, модус и укажите правильность):

а) Все кристаллические вещества имеют определенную температуру плавления. Все металлы являются кристаллическими веществами, следовательно, все металлы имеют определенную температуру плавления;

б) Так как все заряженные частицы отклоняются в магнитном поле, а нейтроны не имеют заряда, значит они не отклоняются в магнитном поле;

в) Некоторые математики обладают способностью к быстрому счету; поскольку все программисты – математики; значит они обладают такой способностью;

г) Учитывая, что многие птицы относятся к водоплавающим, а также тот факт, что большинство птиц улетает зимой в южные страны, можно заключить, что часть водоплавающих также улетает зимой в южные страны.

2. Являются ли силлогистическими следующие умозаключения:

а) Не все то золото, что блестит. Все раскаленное обладает блеском, значит многие раскаленные вещи не являются золотыми;

б) Молекулы химически простого вещества состоят из однородных атомов; водород – простое вещество, следовательно, молекулы водорода состоят из однородных атомов;

в) Тот факт, что жизнь студента истощает силы, на наш взгляд, бесспорен, поскольку любое душевное беспокойство истощает силы, а ведь ни для кого не секрет, что жизнь студента полна беспокойств;

г) Иванов – слесарь; токарь – не слесарь, следовательно, Иванов – не токарь.

3. Используя приемы непосредственных умозаключений, приведите следующие умозаключения к силлогической форме:

а) Поскольку вещества, не имеющие определенной температуры плавления, не относятся к кристаллическим, а все металлы являются кристаллическими веществами, то все они имеют определенную температуру плавления;

б) Ни одно число, которое не делится на 3, не делится на 6; ни одно число, которое не делится на 6, не делится на 12. Отсюда ясно, что все числа, которые делятся на 12, делятся и на 3.

4. Используя имеющиеся у Вас знания, докажите:

а) умозаключения по второй фигуре силлогизма будут неправильными, если одна из посылок не будет отрицательной;

б) для того, чтобы умозаключение по первой фигуре силлогизма было правильно, необходимо, чтобы меньшая посылка не была общим суждением.

5. Опровергните утверждение: «По третьей фигуре силлогизма с необходимостью можно получить не только частные, но и общие заключения».

 

Энтимема (сокращенный силлогизм)

В ходе рассуждения, особенно при передаче мыслей в устной или письменной речи, мы не всегда употребляем силлогизмы в полном, развернутом виде. Иногда формулируется только большая посылка и заключение силлогизма, а меньшая посылка лишь подразумевается. В других случаях не находит явного выражения большая посылка и формулируется лишь меньшая посылка и заключение.

Нередко бывает и так, что даются лишь посылки, вывод из которых предоставляется сделать самому собеседнику или читателю. При этом подразумевается, что вывод возможен по правилам силлогизма.

Силлогизм, в котором выпущена (не выражена явно) какая-нибудь из его частей, называется сокращенным силлогизмом, или энтимемой.

Из сказанного следует, что возможны три вида энтимем (в зависимости от того, какая часть силлогизма не выражена).

Возьмем для примера умозаключение: «Все химически простые вещества состоят из однородных атомов; ни один сплав не есть химически простое вещество; следовательно, ни один сплав не есть вещество, состоящее из однородных атомов».

Это умозаключение можно представить в виде одной из следующих энтимем:

1) «Ни один сплав не есть вещество, состоящее из однородных атомов, так как ни один сплав не есть химически простое вещество». Здесь, как легко увидеть, не сформулирована большая посылка.

2) «Все химически простые вещества состоят из однородных атомов, следовательно, ни один сплав не есть вещество, состоящее из однородных атомов». Выпущена меньшая посылка.

3) «Все химически простые вещества состоят из однородных атомов, а ни один сплав не есть химически простое вещество». Не формулируется заключение.

Возможность сокращенного выражения умозаключений обусловлена тем, что если даны две какие-то части силлогизма, то всегда возможно логическим способом точно установить пропущенную часть.

Основная задача, которую ставит перед собой логика при изучении энтимемы, состоит в том, чтобы указать приемы и правила, которые давали бы возможность точно восстанавливать недостающие части силлогизма.

Когда мы встречаем сокращенный силлогизм, нам необходимо всегда точно осознать, какое именно суждение не выражено, а только подразумевается в данном рассуждении, ибо, иначе невозможно полностью понять это рассуждение. Особенно это важно в дискуссиях, спорах для опровержения тех или иных ложных взглядов. Нередко бывает так, что люди исходят в своих рассуждениях из ложных или сомнительных положений, но не выражают их явно, пользуясь сокращенными формами умозаключений. Чтобы найти ошибку в таком рассуждении и опровергнуть его, надо установить то, что в нем предполагается, но не выражается явно.

В простых случаях подразумеваемые в рассуждении посылки можно установить, не прибегая ни к каким специальным приемам, по общему смыслу рассуждения. Например, если кто-либо рассуждает таким образом: «Данное явление нельзя считать случайным, так как оно имеет свою причину», то ясно, что он исходит из посылки: «Все, что имеет причину, не является случайным» или (что равносильно) «Ни одно случайное явление не имеет причины». Очевидно, что это положение ложно. Следовательно, не состоятелен и вывод, основанный на этом положении.

Но во многих случаях восстановить недостающую часть силлогизма по общему смыслу не так просто. Например, имея энтимему «Иванов пацифист, так как он выступает за мир», можно предположить, по крайней мере, две возможности: либо автор энтимемы рассуждает логически правильно, но употребляет ложную посылку «Все выступающие за мир – пацифисты», либо он имеет в виду истинную посылку «Все пацифисты выступают за мир», но умозаключение его представляет собой неправильный силлогизм.

Однако при восстановлении силлогизма по энтимеме, мы не можем гадать, какой вариант был в действительности и восстанавливаем ту посылку, которую он должен принять, рассуждая логически правильно. То есть придерживаемся своего рода презумпции «логической грамотности»: заподозрить человека в логической неграмотности более неудобно, чем в незнании каких-то конкретных истин.

• Итак, принцип восстановления недостающих частей силлогизма:

если дана какая-либо из посылок и заключение, то недостающая посылка должна быть таким суждением, из которого при сочетании с данной посылкой с логической необходимостью вытекает данное заключение (Это значит, что восстанавливаемый силлогизм должен быть логически правильным независимо от того, как человек рассуждал на самом деле. Возможно, он имел другую посылку и рассуждал неправильно, но мы восстанавливаем именно ту посылку, которую он был обязан принять в силу данной формы.).

Таким образом, операция восстановления недостающей посылки сводится к отысканию указанного суждения. Эта операция всегда легко может быть выполнена в общем виде на основе знания правил и форм правильных умозаключений.

Чтобы уяснить детали этой операции, рассмотрим ее применение к конкретному примеру.

Возьмем энтимему: «Все студенты культурны, поскольку они грамотны».

Прежде всего определим, что дано в этой энтимеме. По смыслу высказывания легко установить, что первое суждение представляет собой заключение силлогизма, а второе – одну из его посылок (поскольку оно приводится как основание первого утверждения).

Далее установим общую форму данных суждений и термины этих суждений и определим, какая из посылок дана и какую следует восстановить. При этом мы имеем в виду, что в данном случае мы можем восстановить умозаключение в форме категорического силлогизма, и должны учитывать, что субъект заключения категорического силлогизма – это меньший термин (S), а предикат заключения – больший термин (Р), а третий термин, имеющийся в данной посылке – средний термин (М).

Очевидно, что в данном случае мы имеем заключение: «Все студенты (S) есть культурные люди (Р)» и меньшую посылку: «Все студенты (S) есть грамотные люди(М)», поскольку «они» – это студенты, то есть субъект заключения. Недостающая посылка является, следовательно, большей.

Отвлекаясь от конкретного содержания данных суждений, представим их в общем виде: «S есть М» и «S есть Р».

При данной посылке мы можем восстановить правильный силлогизм по схеме первой фигуры.

В таком случае большая посылка должна представлять связь терминов М – Р.

Исходя из правил силлогизма, устанавливаем, что это суждение должно быть общеутвердительным: «Все М есть Р». Подставляя конкретное значение терминов, получим: «Все грамотные люди есть культурные люди».

Теперь мы можем возразить человеку, который рассуждает в форме данной энтимемы, указав ему на то, что он употребляет ложную посылку (В случае же употребления им истинной посылки «Все культурные люди есть грамотные люди» он рассуждает неправильно: средний термин оказывается нераспределенным в обеих посылках.).

Возможно, что при выявлении недостающей посылки, то есть восстанавливая энтимему в полный силлогизм, мы можем получить две различные формы правильного силлогизма с различными, но равнозначными посылками. Именно эти две возможности указаны в приведенной выше энтимеме: «Данное явление нельзя считать случайным, так как оно имеет свою причину»:

 

 

Ясно, что это уже модус Cesare второй фигуры.

Однако, поскольку мы выявляем недостающую посылку в конечном счете для того, чтобы оценить, является ли она истинной или ложной, постольку упомянутые различия для нас не играют роли: равносильные посылки либо обе истинны, либо обе ложны. В обоих случаях рассмотренного нами примера мы скажем автору энтимемы: «Вы употребляете ложную посылку!»

Надо иметь в виду, что поскольку при восстановлении силлогизма мы требуем, чтобы этот силлогизм был правильный, постольку не всегда можно по данной энтимеме восстановить такой силлогизм. И это означает, что человек, высказывающий данную энтимему, рассуждает логически неправильно. Так, в частности, рассуждает человек, высказывающий энтимему: «Так как все жидкости упруги, значит некоторые металлы не упруги».

При наличии энтимемы с пропущенным заключением восстановление силлогизма сводится к тому, чтобы вывести это заключение. Если же даны две посылки, из которых не следует никакого заключения по правилам категорического силлогизма, то это не энтимема – согласно данному выше определению эитимемы.

Трудности восстановления силлогизмов по энтимеме могут быть связаны с тем, что в естественном языке категорические суждения формулируются далеко не стандартным образом и часто, прежде чем привести их к стандартной форме, нужно разобраться в их смысле.

 

Упражнения

 

Восстановите силлогизмы по энтимемам:

1) Данный силлогизм имеет три термина и поэтому он правильный;

2) Как все эгоисты, трус не является великодушным;

3) Ничто разумное никогда не ставило меня в тупик, а Ваш вопрос поставил меня в тупик!

4) Спички – очень нужная вещь в путешествии. Отправляясь в путешествие, все лишнее следует оставлять дома;

5) Раз все люди разумны, то ни одна улитка не разумна;

6) «Аи, Моська! Знать она сильна, что лает на слона»;

7) Все шутки для того и предназначены, чтобы смешить людей; ни один парламентский акт не шутка.

Сокращенными – энтимематическими – могут быть не только формы категорического силлогизма, но и те выводы, которые рассматривались в логике высказываний и выводы из суждений с отношениями, с которыми мы встречались в логике предикатов. Например: «Это можно сказать либо не помня, что говоришь, либо заведомо говоря неправду. Следовательно, этот человек говорит явную неправду» или «Поскольку Нюра – внучка Татьяны Петровны, значит, Иван Иванович – дядя Нюры».

Наши рассуждения в естественном языке обычно энтимематичны. При этом человек, который высказывает соответствующую энтимему, может даже не осознавать, какие посылки он использует в своем умозаключении, а само умозаключение может быть настолько сложным, что представляется трудным оценить, является ли оно правильным. Отсюда возможны споры, следует ли что-то из чего-то. Можно быть уверенным, что у многих читателей возникнут трудности, например, в связи с последней из приведенных энтимем. Более того, едва ли ему покажется очевидной и одна из подразумеваемых посылок этой энтимемы, а именно, общая посылка: «Для всякого человека х, у, z, если у – внучка – х и z – сын х, и z – не родитель у, то z дядя у». Фактически здесь подразумевается дополнительный анализ – вывод указанной посылки из определений понятий «бабушка», «внучка», «дядя», «сын», «родитель».

Обычно в практике естественных рассуждений мы решаем вопросы о правильности тех или иных умозаключений на основе интуиции. Однако нередко она является сомнительной, а иногда и бессильной. Общий метод решения подобных вопросов – это метод формализации выводов. Осуществляя формализацию некоторого вывода, мы выявляем всю ту информацию, которая фактически в нем используется и потому, следовательно, можем оценивать с точки зрения истинности используемы человеком посылки. При этом может оказаться, что неправильность содержательного рассуждения человека состоит именно в том, что он – сознательно или несознательно – использует неистинные посылки.

 ПРАВДОПОДОБНЫЕ ВЫВОДЫ (ПРАВДОПОДОБНЫЕ УМОЗАКЛЮЧЕНИЯ). ПОНЯТИЕ ИНДУКТИВНОГО СЛЕДОВАНИЯ

Правдоподобные выводы в настоящее время часто называют индуктивными, противопоставляя их дедуктивным. Основная разница между теми и другими усматривается в том, что дедуктивные выводы являются достоверными, а именно, они – при условии их правильности – обеспечивают истинность заключений при истинности посылок. Индуктивные же выводы обеспечивают лишь некоторую степень правдоподобия заключений, некоторое повышение вероятности их истинности при истинности посылок. Однако в традиционной логике индукцией называли лишь некоторый определенный вид правдоподобных выводов, а именно, так называемые выводы от отдельного (или от частного) к общему. При этом индукцию также противопоставляли дедукции, но последнюю понимали также значительно более узким образом, чем теперь. А именно, как выводы, противоположные индукции по своей направленности, то есть как выводы от общего к частному (или отдельному). Однако многократно отмечалось, что эта характеристика дедукции – при современном ее понимании – явно несостоятельна. Несостоятельность эта проявлялась исторически и в том, что к дедуктивным выводам относили многие формы умозаключений, которые не удовлетворяли их характеристике как выводов от общего к частному (или отдельному): условные, условно-категорические, условно-разделительные, силлогистические выводы, например, вида «Некоторые S суть Р ╞ Некоторые Р суть S» и др. Вместе с тем характеристика выводов, называемых в ранее индуктивными, как выводов от частного (или отдельного) к общему, действительно указывает на их существенную особенность. Они естественно выделяются как вид правдоподобных выводов.

Учитывая сказанное относительно употребления терминов «дедукция» и «индукция», целесообразно термин «дедукция» употреблять в современном, упомянутом выше, ее смысле, а термин «индукцию» понимать так, как она понималась исторически. К тому же для выводов, которые сейчас называют индуктивными, есть другое и более подходящее название – правдоподобные. В таком случае индукция не противопоставляется дедукции (и, как мы увидим далее – см. «полная индукция», среди индуктивных выводов могут быть и дедуктивные), противопоставляются лишь выводы дедуктивные и правдоподобные. Это избавит нас от тех терминологических трудностей, которые часто возникают сейчас в современной логике.

Имеются существенные различия в степени разработки понятий дедуктивных и правдоподобных выводов. Дедуктивные имеют определенные формы, подчинены определенным законам, чем и обусловлена их достоверность. Основу их составляет уже известное нам понятие логического следования (теперь можно добавить, дедуктивного следования). Это понятие, как мы уже знаем, дает определенный критерий, а именно, указывает на необходимое условие логической правильности дедуктивных выводов: если вывод правилен, то между его посылками и заключением имеется отношение логического – дедуктивного – следования. Если же иметь в виду простые выводы (формы умозаключений, называемые в символической логике правилами, по которым осуществляются сложные выводы вроде «  или – в естественном языке – «Все S суть Р ╞ и одно не-Р не есть не-S» и т.п.), то эти выводы непосредственно представляют собой логические следования и, таким образом, наличие логического следования для них является необходимым условием их правильности. Говоря о формах правдоподобных выводов, имеют в виду простые выводы. Теория этих выводов разработана в значительно меньшей степени. Как правило, выделяют два основных вида этих выводов – индукцию и аналогию. Однако, к их числу следует присоединить более важный (по крайней мере не менее важный) вид правдоподобных выводов, который мы назовем ниже образно-дедуктивным методом обоснования научных гипотез в теориях так называемого гипотеко-дедуктивного типа. По существу, имеются в виду неаксиоматазированные теории, к числу которых принадлежит, в частности, большинство естественно-научных теорий (физика, химия, биология, астрономия и т.д.).

Для научной разработки этих и, возможно, других форм правдоподобных выводов необходим, очевидно, аналог дедуктивного логического следования. Таковым является так называемое индуктивное следование. (Данное название появилось в связи с указанным выше отождествлением правдоподобных выводов с индуктивными. Но отказавшись от этого отождествления, мы вынуждены сохранить упомянутое название отношения логического следования, поскольку термин «правдоподобное» логическое следование был бы не совсем удачным.)

По аналогии отношения дедуктивного следования к простым дедуктивным выводам индуктивное следование должно составлять основу правильных правдоподобных выводов. Точнее говоря, поскольку речь идет о простых правдоподобных выводах, их логические формы должны представлять как раз отношение индуктивного следования между их посылками и заключением. Однако, как мы увидим далее, это выполняется не для всех известных правдоподобных выводов, что указывает на необходимость уточнения в таких случаях понятия логических форм этих выводов.

 

ИНДУКТИВНОЕ СЛЕДОВАНИЕ

Индуктивное следование – это такое отношение между высказываниями А₀ и В₀, которое имеет место е. т. е. В₀ не является дедуктивным следствием А₀ и вероятность В₀ при условии, что истинно А₀ больше, чем вероятность В₀ самого по себе.

 

 

Существенно обратить внимание на то, что если В ╞ А (из В дедуктивно следует А), то  Но обратное неверно. Этот способ установления индуктивного следования между A и В на основе дедуктивного следования между В и А называется принципом обратной дедукции. При этом для отношении дедуктивного следования, которое здесь имеется в виду, исключаются случаи парадоксальности этого отношения, каковыми, как мы уже указывали выше, являются случаи, когда А есть отрицание некоторого логического закона рассматриваемой системы, или, когда В есть какой-нибудь закон логики (это значит, что по существу здесь имеется в виду релевантное следование – связь между высказываниями по содержанию).

Например, высказывание вида p v q (при любых конкретных содержаниях р и q) индуцирует р (как, впрочем и q). Наличие этого отношения можно установить табличным способом, пользуясь уже известным читателю табличным определением дизъюнкции, согласно которому это высказывание ложно лишь в случае, когда ложны оба члена дизъюнкции – р и q. Выпишем все возможные распределения истинностных значений по переменным р и q:

 

 

Очевидно, что вероятность истинности р(Р(р)) равна 1/2 (отношение благоприятных случаев – 2 – к общему числу случаев – 4). С учетом же допущения об истинностиp v q, надо вычеркнуть случаи, где это высказывание ложно. В результате получим:

 

 

Таким образом, при наличии предположения об истинности посылок уменьшается общее число возможных случаев, поэтому может изменяться вероятность истинности следствия.

Вообще говоря, для высказываний А и В возможны три случая:

а) вероятность В при учете, что истинно А, повышается (по сравнению с вероятностью В самого по себе) то есть Р(В)А > Р(В),– наличие позитивной релевантности между А и В;

б) Р(В)/А < Р(В), то есть вероятность В при условии истинности А понижается – наличие негативной релевантности между А и В.

в) Р(В)/А = Р(В) – отсутствие релевантности между А и В. В нашем случае вероятность истинности р при истинности р v q равна, очевидно, 2/3. Таким образом, поскольку 2/3 > 1/2, то есть Р(р) / (р v q) > Р(р) можем констатировать, что между р v q и q имеется позитивная релевантность (индуктивное следование),– то есть отношение 

Обратам внимание, что в данном случае наличие индуктивного следования мы могли бы установить по принципу обратной дедукции, поскольку знаем, что р ╞ p v q(хотя сам этот принцип доказывается посредством использованием указанного табличного метода анализа).

При определении индуктивного следования между двумя формулами (или между множеством формул и некоторой формулой) с учетом некоторой теории Т первым шагом является ограничение всех возможных случаев в таблице за счет вычеркивания тех, которые противоречат теории. В остальном вычисление P(В) и P(В)/Аосуществляется так же, как указано в примере.

 

Основные виды правдоподобных выводов (умозаключений)

Наиболее общей и простой формой индуктивных выводов являются выводы по принципу обратной дедукции – обратно-дедуктивный метод обоснования гипотез. Другими формами являются известные в традиционной логике индуктивные выводы и выводы по аналогии.

ОБРАТНО-ДЕДУКТИВНЫЙ МЕТОД ОБОСНОВАНИЯ ГИПОТЕЗ (В СОСТАВЕ НЕАКСИОМАТИЗИРОВАННЫХ ТЕОРИЙ)

Речь здесь идет о подтверждении гипотетических объяснений явлений и законов в теориях. По форме эти выводы представляют собой умозаключения типа:

Из А дедуктивно следует В и В истинно, следовательно, более вероятно, чем прежде, что истинно А.

Где А – как раз упомянутая гипотеза, а В – некоторое следствие из нее фактического характера.

Словесно принцип такого способа подтверждения гипотез формулируют иногда так:

Если подтверждаются следствия из гипотезы, то подтверждается и сама гипотеза.

Однако в данных двух случаях употребления слово «подтверждение» имеет два смысла:

1) Для следствий «подтверждает» означает «оказывается истинным».

2) Для гипотез же «подтверждение» означает, как уже сказали, «повышение степени ее правдоподобия» и, говоря о способе подтверждения гипотез, мы имеем в виду здесь именно этот смысл слова.

Если следствия гипотезы А постоянно оправдываются (подтверждаются), то в конце концов гипотеза становится практически (но не теоретически, не логически) достоверной. Многие утверждения науки, оправданные таким образом, не вызывают у ученых никаких сомнений. Иногда даже говорят, что они «строго доказаны». Так, например, авторы учебника физики для 10-го класса пишут, что основные положения молекулярно-кинетической теории (вещество состоит из частиц; эти частицы беспорядочно движутся; частицы взаимодействуют друг с другом) «строго доказаны с помощью опытов (Мякишев Г.Я., Буховцев Б.Б. Физика.– М.: Просвещение, 1992.– С. 7.)».

Утверждения такого рода не являются точными: строгого доказательства здесь нет. Таковым может быть только логическое доказательство (см. гл. XI). Вообще, научные объяснения тех или иных явлений, каковыми являются и положения молекулярно-кинетической теории, с теоретической точки зрения всегда гипотетичны – для них не существует строгих доказательств.

Подтверждение лишь увеличивает вероятность того, что высказывание истинно, и в этом смысле является способом обоснования нашего знания (см. гл. XI). Эта вероятность может увеличиваться, стремясь к 1 как к своему пределу, но вероятность, равная 1, то есть логическая достоверность, не может быть достигнута подобно тому, как ветви гиперболы постоянно приближаются к своим асимптотам, никогда не достигая их, или как число я при уточнении его вычисления приближается к 3, 15, никогда, однако, не достигая этого числа. Вероятность, равная 1, может быть результатом лишь логического доказательства. Таким образом, между практической и логической достоверностью есть качественная разница: первое есть знание о том, что некоторое высказывание истинно с вероятностью, весьма близкой к 1 (которую практически можно принять за 1); второе есть знание о том, что высказывание истинно, то есть ситуация, которую оно описывает, имеет место в действительности. Здесь же мы различаем два способ обоснования: подтверждение и доказательство.

Согласно понятию дедуктивного вывода, если дедуктивно выводимое из некоторой гипотезы следствие оказывается ложным, то это указывает на ложность гипотезы. Это наводит на мысль, что гипотезы в таких случаях должны отбрасываться (исключаться из теории). Но обычно – в практике научного познания – пытаются тем или иным способом уточнить гипотезу так, чтобы упомянутое следствие из нее больше не было выводимо.

Следует отметить также случаи, когда выводимое из гипотезы следствие не просто в какой-то степени ее подтверждает, но как кажется, и доказывает гипотезу. Это имеет место в тех случаях, когда наличие ситуации, на которую указывает это следствие кажется невозможным объяснить иначе как признав истинность гипотезы. Обнаружение таких следствий из гипотез называют иногда решающим экспериментом (experimentum crucis) в процедуре проверки гипотезы. Например, в качестве следствия из утверждения о том, что Земля вращается – которое по крайней мере первоначально рассматривалось как гипотеза – является явление, известное под названием «маятник Фуко», состоящее в том, что вращается плоскость качания маятника, расположенного достаточно далеко от экватора. Это явление не удается объяснить иначе, как вращением Земли. Однако в современной методологии к таким методам доказательства гипотез относятся довольно скептически, имея в виду, что относительна сама «возможность найти другое объяснение некоторого явления». Эта «невозможность» может быть обусловлена каким-то недостатком наших знаний.

ИНДУКТИВНЫЕ ВЫВОДЫ (ИНДУКЦИЯ), ИХ ВИДЫ И ХАРАКТЕРИСТИКА

Под индукцией в традиционном смысле слова имеются в виду формы эмпирического (Мы рассматриваем здесь индуктивные выводы, а именно как форму эмпирического познания, как они понимались в традиционной логике. В современной науке имеется также математическая индукция. Студенты, очевидно, знакомы с этой формой познания из школьною курса математики, где она используется в доказательстве многих теорем. Мы не касаемся здесь этой формы, поскольку она относится к методам теоретического познания.) познания – выводы, заключениями которых являются – общие знания вида «Все S суть Р»  – о принадлежности некоторою свойства Р всем предметам класса S, а посылками – знания о принадлежности свойства Р либо каким-то отдельным предметам a₁, a₂, ..., а_nданною класса S, либо предметам каких-то видов S₁, S₂, ..., S_m этого класса. В первом случае индукцию характеризуют как умозаключение от отдельного к общему, во втором – как умозаключение от частного к общему. Поскольку во втором виде выводов сами посылки суть высказывания общего вида «Все S_i суть Р» (i = 1, 2, ..., m), которые могут представлять, собой, в свою очередь, заключения выводов первою типа, мы остановимся прежде всего на этом первом.

Содержательно вывод состоит в том, что перебираются тем или иным образом отдельные предметы класса S a₁, a₂, ..., а_n,– некоторые или все. И при этом дня каждого а_i устанавливается, обладает ли он свойством Р, то есть верно ли высказывание P(a_i). Если в каждом случае последнее верно, то заключают, что все предметы Sобладают указанным свойством Р. Если класс предметов S довольно широк и возможно даже практически бесконечен, как положим класс деревьев, и тем более растений вообще, то естественно перебору может подвергнуться только некоторая его часть, и заключение в этом случае, например, что все растения ведут неподвижный образ жизни, более или менее проблематично и используется в науке только как гипотеза.

Когда просмотрены не все предметы класса S, индукция называется неполной, в противном случае – полной. Если перебор предметов в неполной индукции осуществляется случайным образом, то индукция называется популярной и характеризуется обычно как вывод на основе простого перечисления предметов класса S, в котором нет противоречащих случаев. Наряду с популярной выделяют индукцию научную, отличающуюся применением особых приемов отбора упомянутых отдельных предметов класса S. Выводы как полной индукции, так и неполной популярной индукции характеризуют обычно как умозаключения о присущности всем предметам классаS свойства Р на основе простого перечисления предметов этого класса, в котором – перечисления – не встречается противоречащих случаев.

Для выявления логической формы – общей для всех индуктивных выводов от отдельного к общему – необходимо уточнить понятие посылок индуктивных выводов. Из только что приведенной выше характеристики этих выводов видно, что в каждой посылке его для каждого предмета а₍. должно быть заключено не только знание о том, что этот предмет обладает свойством Р, что выражается в высказывании «Р(а_i)», но также, в первую очередь, и то, что он принадлежит классу S, что означает истинность для него высказывания «S(a_i)».

Таким образом, каждая посылка должна представлять собой конъюнкцию «S(a_i) & Р(а_i)». С учетом всего сказанною, логическая форма всех упомянутых видов индуктивных выводов может быть представлена так:

 

 

Существенно заметить, однако, что если имеется в виду не просто конечная форма вывода, а сам процесс его осуществления, то есть отбор посылок и движение от них к заключению, то надо иметь в виду, что конъюнкция в посылках должна пониматься не как обычная (охарактеризованная в гл. III), а как направленная конъюнкция. От обычной она отличается некоммутативностью, иначе говоря, она не допускает замену «A & В» на «В & A». С такой конъюнкцией мы имеем дело, например, в высказывании «Петров хорошо подготовился к экзамену и удачно сдал его» (ясно, что при перестановке членов получим нелепость). Точнее говоря, знак «&» мы употребляем здесь вместо обычного союза «и» который в естественном языке нередко используется как направленная конъюнкция (последовательность событий). Дело в том, что при формировании посылок индуктивного вывода мы каждый раз прежде всего выбираем предмет (а_i) из класса S, то есть такой, для которою верно S(a_i), и затем устанавливаем у него наличие свойства Р. Если окажется, что он не обладает свойством Р, то процесс индукции вообще кончается, ибо при этом обнаруживается случай, противоречащий предполагаемому заключению.

Упомянутая замена в посылках индуктивных выводов обычной конъюнкции направленной не вносит каких-либо осложнений в анализ выводов, поскольку условием истинности направленной конъюнкции является то же, что и для обычной, а именно истинность обоих ее членов (но взятых в соответствующем порядке), а из истинности конъюнкции следует истинность обоих ее членов.

 

Пример

 

Посылки:

Медь (а₁) является металлом (S) и медь (а₁) проводит электрический ток (Р).

Никель (а₂) является металлом (S) и никель (а₂) проводит электрической ток (Р).

Аналогично: для а₃, а₄, а₅ ... (железо, золото, свинец и др.).

Заключение: Все металлы (S) проводят электрический ток (Р). (Или, что то же: «Для любого предмета х верно, что если он является металлом (S), то он проводит электрический ток (P)»).

В формализованном языке  поскольку S – не пусто.

Таким образом, посылки указывают на повторяемость сочетания: наличие признака S у некоторого предмета а_i, в сочетании с признаком Р, а заключение – на то, что подобная повторяеемость имеет место в любом случае.

 ПОЛНАЯ И НЕПОЛНАЯ ИНДУКЦИЯ

Как мы уже говорили, в зависимости от того, перечислены ли в посылках все или не все предметы класса S, индукция называется полной или неполной.

В полной индукции, строго говоря, должна быть добавлена еще одна посылка: «Перечисленные предметы a₁, a₂, ..., а_n исчерпывают класс предметов S».

Применения полной индукции нередки в науке и особенно распространены в повседневной жизни. Этим способом получены наши знания, относящиеся ко всем так называемым большим планетам Солнечной системы, о том, например, что все они светят отраженным светом, вращаются вокруг своей оси и вокруг Солнца и т. д. К этому же типу умозаключений будет принадлежать и вывод о том, что «Все студенты некоторой группы сдали какой-то зачет или экзамен», к которому мы приходим, просмотрев соответствующие ведомости.

 

 

Первая посылка здесь представляет собой объединенное знание о том, что все рассмотренные предметы a₁, ..., а_n относятся к классу S и исчерпывают его.

Обычно при рассмотрении индукции этого вида обсуждается вопрос: дает ли она в заключении новое знание? Ответить на него можно довольно просто: поскольку заключение является общим знанием, оно, безусловно, является новым по сравнению с тем, что дано в посылках. Но оно, как и во всяком дедуктивном умозаключении, не содержит никакой информации, кроме той, что заключена в совокупности посылок (о знании и информации см. § 36). К тому же общее знание по сравнению с совокупностью разрозненных знаний об отдельных предметах класса имеет определенную ценность в том, что оно может наводить на мысль о наличии некоторой связи между признаками S и Р и таким образом стимулировать дальнейшее развитие знания. И ясно, конечно, что оно более удобно для использования.

Вместе с тем научную значимость полной индукции как приема познания нельзя преувеличивать, тем более, что ограничены и возможности ее применения. Теоретически она осуществима, лишь когда класс предметов S является конечным. Но конечным является, например, и класс молекул, атомов, животных на Земном шаре в каждый данный момент времени и др. Ясно, что для осуществления выводов по полной индукции мы должны иметь практическую возможность просмотра и перебора предметов этого класса.

Неполная индукция более распространена в научном познании, так как именно она позволяет получать общее – но правда гипотетическое – знание, относящееся к практически бесконечным, открытым классам, а также и к конечным, но практически не перечислимым в силу большого числа их элементов. Именно с такими классами имеет обычно дело наука и общее знание о них представляет большую ценность. Результатом выводов такого рода являются утверждения науки о том, что, например, все млекопитающие – позвоночные и теплокровные, все вороны – черные, что все жвачные – парнокопытные, все кислоты окрашивают лакмусовую бумажку в красный цвет, а все щелочи – в синий и т.п.

Однако выводы по методу неполной индукции не являются достоверными, заключения их приемлемы в принципе лишь как гипотезы. Конечно, в дальнейшем такие обобщения – типа «Все S суть Р» – могут приобретать характер несомненно истинных утверждений либо в силу многочисленных, постоянных подтверждений фактами, либо в результате специального – теоретического их обоснования, состоящего в выявлении необходимой связи между признаками S и P.

Заключения неполной индукции нередко бывают и ошибочными. Классическим стал пример индуктивного обобщения «Все лебеди белые», которое действительно имело место на определенном этапе развития науки. Это заключение индукции возникло в результате наблюдения лебедей в Европе, Азии, Америке и некоторых других изученных местах. Потом оказалось, что в Австралии есть черные лебеди. До некоторых пор также наблюдаемые факты подводили к обобщению – «Все тела при нагревании расширяются». Оказалось, однако, дело обстоит не так: вода при нагревании от 0 до 4°С, наоборот, сжимается; исключения составили также чугун, висмут.

Для того, чтобы использовать метод индуктивного обобщения более эффективным и надежным способом, полезно знать некоторые условия, повышающие степень правдоподобия получаемых утверждений. Наиболее элементарное из них состоит в том, что для перехода к заключению надо рассматривать по возможности большее число случаев. Когда вывод осуществляется на основании недостаточно большого числа случаев, говорят, что допускается ошибка «поспешного обобщения». Водитель автобуса на одной из остановок открывает дверь, но никто из пассажиров не выходит и никто не входит. На второй остановке повторяется то же самое, на третьей – то же. Четвертую остановку водитель проезжает не останавливаясь и на возмущенный голос пассажира «Почему нет остановки?» отвечает: «Я уже несколько раз зря останавливался, думал, что все едут до конца!»

Более существенным условием повышения степени правдоподобия заключений неполной индукции является специальный отбор перечисляемых в посылках случаев. Так, используя посылки, представляющие собой положительные инстанции, степень правдоподобия заключения повышается, если рассматриваются максимально разнородные предметы класса S, если выбираются предметы из разных подклассов этого класса, то есть учитываются предметы различных видов этого рода. При выполнении этого условия возникает основание предполагать, что признак Р каким-то неслучайным образом связан с S, что последний детерминирует его. Именно это, очевидно, имел в виду русский логик М. Каринский, утверждая, что индуктивный вывод тогда является научным, когда мы можем предполагать, что рассмотренные случаи являются «полномочными представителями класса S», то есть они имеют свойство Р не в силу каких-то их особых качеств, отличных от S, а в силу наличия у них именно признака S.

В случаях же использования посылок смешанного характера, вида S(a_i) & Р(а_i) и не-Р(а_j) & He-S(a_j),– когда заключение имеет вид «Все S суть Р» – полезно выбирать, наоборот, предметы а_i и а_j, по возможности наиболее сходные между собой. Идеи, которые здесь имеются в виду, нашли выражение в двух упомянутых ранее и рассматриваемых ниже методах установления причинной зависимости между явлениями, соответственно – в методе сходства и методе различия.

В принципе, все эти методы могут быть использованы как средства повышения степени правдоподобия индуктивных обобщений. Они могут применяться как в процессе построения таких обобщений, так и к уже полученным результатам индукции с целью выработки убеждения о существовании какой-то необходимой связи между признаками S и Р.

Индукция, в которой применяются эти или подобные приемы, называют обычно научной индукцией. В противном случае ее характеризуют, как мы уже отмечали, как «индукцию через простое перечисление при отсутствии противоречащих случаев» или, иначе, как популярную индукцию.

Убеждение о существовании необходимой связи между S и Р при индуктивных заключениях вида «Все S суть Р» возникает во многих случаях интуитивно. В зависимости от степени такого убеждения одни утверждения воспринимаются как более надежные, а другие кажутся сомнительными даже при выполнении многих условий, повышающих степень правдоподобия умозаключений неполной индукции. Так, индуктивные заключения о том что все кислоты окрашивают лакмусовую бумажку в красный цвет, а щелочи – в синий, что все жидкости упруги и т. д., воспринимаются в науке даже как достоверные. Но отнюдь не такими надежными кажутся, например, заключения, что все вороны черные, а медведи, живущие на Северном полюсе,– белые, хотя второе из двух последних утверждении является более правдоподобным, поскольку для него есть дополнительные основания, которые используются в известном объяснении этой особенности окраски данных животных. Она объясняется как результат длительного приспособления медведей к окружающей среде.

К этим традиционным представлениям о структуре индуктивного вывода необходимо сделать дополнение. Дело в том, что посылками индуктивного вывода с заключением «Все S суть Р» могут быть не только конъюнкции утвердительных высказываний «S(а_i) & Р(а_i)» («положительные инстанции» – по терминологии Ф. Бэкона), но и отрицательных «не-Р(а_j) & нe-S(a_j)» отрицательные инстанции).

Первый член в этих конъюнкциях указывает на тот класс, предметы которого надо «перебирать» для получения индуктивного заключения. В одном случае – класс предметов, обладающих свойством S, в другом – не обладающих свойством Р. Последние также подтверждают заключение, как и положительные, поскольку высказывание «Все S суть Р» при непустом не-Р,– что предполагается – эквивалентно «Всякое не-Р есть не-S» (см. непосредственные выводы из категорических суждений). Так, наряду с утверждением «Данная птица есть лебедь и она белая», подтверждающим высказывание «Все лебеди белые», ту же функцию выполняет и утверждение «Данная птица не белая (не-Р) и она не является лебедем (не-S) (Некоторые логики из этого факта выводят так называемый парадокс подтверждения (парадокс «Черный ботинок»), который состоит в том, что утверждение «Данный ботинок черный (не является белым) и при этом не является лебедем» якобы подтверждает указанное высказывание «Все лебеди белые», поскольку оно якобы эквивалентно высказыванию «Ни один не белый предмет не является лебедем». Фактически же эквивалентным ему является «Ни одна не белая птица не является птицей лебедем». В рассуждении, которое приводит к данному парадоксу, имеется ошибка. Она состоит в том, что в качестве рода понятия «лебедь» берется множество предметов вообще, или, точнее, по-видимому, множество материальных предметов, которое не является естественной областью определения предикатора «лебедь» (см. §6). Таковой (областью определения предикатора «лебедь») должно быть, очевидно, множество птиц. В силу указанного выше требования общности рода для понятий субъекта и предиката в категорическом суждении (см. § 36) это же множество должно быть взято в данном случае также и в качестве области определения и предикатора «белый». Как мы уже говорили, неправильный выбор рода является ошибкой в формулировках понятий и высказываний. И как увидим далее, эта ошибка лежит в основе ряда софизмов.)». Использование отрицательных инстанций полезно, например, при выводе высказываний видов «Ни одно не-S не суть не-Р» (которое фактически при этом заменяется на эквивалентное «Все Р суть S».)

Как уже могли заметить, понятия положительных и отрицательных инстанций являются относительными. Они определяются относительно заключения индукции. В указанных их формулировках подразумевалось заключение вида «Все S суть Р». Если, например, заключением индукции является высказывание «Все S суть не-Р» или «Ни одно S не суть Р», то положительными инстанциями будут высказывания вида «S(а_i) & не-Р(а_i)», а отрицательными – «Р(а_i) & не-S(а_i)». Таким образом, в зависимости от того, какого вида инстанциями являются посылки индукции, возможно различить три вида индуктивных выводов: положительная индукция, отрицательная и смешанная. В первой все посылки суть положительные инстанции, во второй – отрицательные, а в третьей имеются и те и другие. Различение первых двух случаев не является существенным, поскольку один превращается в другой простым преобразованием заключения. Если в положительной индукции заключение «Все S суть Р», то, заменив его на «Все не-Р суть не-S» или «Ни одно не-Р не суть S», мы получим отрицательную индукцию; аналогично отрицательная индукция превращается в положительную. Выделение же третьего вида индукции является весьма существенным, ибо, она обеспечивает, вообще говоря, высокую степень правдоподобия заключения по сравнению с чисто положительной или чисто отрицательной индукцией.

Напомним, что употребляя некоторые суждений вида «Все S суть Р» или «Ни одно S не есть Р» мы имеем в виду, что субъект и предикат этого суждения – это общие описательные имена (понятия) (См. § 6 и § 16.) видов xS(x) и хР(х), где область х – D – это общий род наших понятий; предмет а_;, фигурирующий в посылках,– это предмет из этого рода. Но наличие члена S(а_i) в посылке S(а_i) & Р(а_i) указывает на то, что в положительных индукциях достаточно осуществить перебор класса S (более узкого, конечно, чем тот класс, который является родом рассмотренных понятий). Смешанная же индукция указывает на то, что полезно не ограничиваться перебором только предметов S; целесообразно в той или иной мере выходить за пределы этого класса, а именно «заглядывать» в класс не-Р.

Исходя из сформулированною выше понятия индуктивного следования, как позитивной релевантности, можно убедиться, что между посылками и заключением неполной индукции это отношение имеет место. И это является определенным теоретическим оправданием данной формы вывода. Однако при этом существенно, что позитивно релевантными по отношению к заключению являются именно посылки вида S(а_i) & Р(а_i), как и  (с направленной конъюнкцией). Обычно в учебниках логики вместо посылок этого вида берут отдельно Р(а₁), Р(а₂), ..., Р(а_т) и S(a₁), S(a₂), ..., S(a_m) (заключительную последовательность обычно сокращенно представляют в виде  При этом трудно определить, следует ли (индуктивно) заключение «Все S суть Р» из этой совокупности посылок, поскольку оказывается, что посылки вида S(a_i) снижают степень правдоподобия заключения, а посылки вида P(a_i) – наоборот повышают ее.

 

ИНДУКЦИЯ ОТ ЧАСТНОГО К ОБЩЕМУ

Индукция от частного к общему, как мы уже говорили, есть вывод, заключением которого, как и в индукции от отдельного к общему, является общее знание «Все Sсуть Р», но посылками служат знания не об отдельных предметах класса S, а общие высказывания видов «Все S₁ суть Р» – «Все S₂ суть Р» и т. д., где S₁, S₂ – какие-то виды класса S, выделенные по какому-нибудь одному основанию. Например, железо – хороший проводник электричества, медь – хороший проводник электричества, цинк – хороший проводник электричества и т.д.; заключение «Все металлы – хорошие проводники электричества». Подразумевается при этом, что железо, медь, цинк – виды металлов, и при этом имеются в виду не химические элементы железо, медь, цинк и т. д. (о которых было бы бессмысленно утверждать наличие признака «быть хорошим проводником электричества»), а соответствующие вещества. Поэтому утверждение «Железо – хороший проводник электричества» есть просто сокращение общего высказывания «Всякий кусок железа является хорошим проводником электричества», аналогично здесь имеем общее знание о видах металлов. Степень достоверности заключения о всех металлах зависит, во-первых, от того, все ли виды металлов рассмотрены, то есть является ли индукция полной или неполной относительно самих видов. Если индукция является неполной относительно видов, то степень правдоподобия заключения зависит от количества рассмотренных видов. Во-вторых, надежность или ненадежность заключения зависит от того, насколько состоятельно обобщение, относящееся к отдельным видам.

Эти обобщения сами по себе могут быть результатами популярной или научной индукции, или же теоретическими обобщениями, подобными применяемым, например в геометрии, при доказательстве ее теорем: «Всякий треугольник имеет сумму углов, равную 180°, «Во всяком ромбе диагонали взаимно перпендикулярны» и т.п. Именно в таком виде индукция от частного к общему применяется в некоторых случаях в математике. Для доказательства, например, теоремы «Вписанный в окружность угол измеряется половиной дуги, на которую он опирается». Рассматривают обычно три случая – три вида возможных случаев расположения центра окружности по отношению к вписанному углу: 1) центр окружности находится внутри вписанного угла; 2) центр находится на какой-нибудь стороне угла; 3) центр окружности находится вне угла. Для каждого случая теорема доказывается отдельно и затем, поскольку все случаи учтены, теорема формулируется общем виде (для любого вписанного в окружность угла).

Индуктивные выводы от частного к общему, в которых сами посылки представляют собой индуктивные обобщения, весьма редки в практике научного познания. Возвращаясь к рассмотренному примеру заключения о хорошей электропроводности всех металлов, естественно поставить вопрос: не было бы проще и не менее надежно получить это общее знание, просто рассматривая отдельные металлы, то есть посредством индукции от отдельного к общему (в данном случае, очевидно, неполной индукции). Обращение к видам металлов при этом возможно лишь в том смысле, что выбор случаев из разных видов гарантирует выполнение указанного выше условия повышения степени правдоподобия заключения неполной индукции за счет рассмотрения качественно разнообразных предметов изучаемого класса. В практике научного познания поступают обычно таким образом. (Не случайно, по-видимому, индукция от частного к общему в учебной литературе часто вообще не рассматривается.)

Индукция и подтверждение. Однако сутью индуктивного процесса и основой индуктивных обобщений является накопление определенной информации фактического характера, на основе которой и делается обобщение. Таким образом, индукция представляет собой форму познания, противоположную рассмотренному выше процессу подтверждения научных гипотез или, что ближе к сути дела, подтверждение и индукция – это два в определенном смысле противоположных метода познания, но взаимосвязанные и дополняющие друг друга: фактический материал, накопленный в процессе индуктивных обобщений, углубляется и расширяется затем в процессе проверки и подтверждения возникающих индуктивных обобщений. В единстве эти методы составляют основное логическое содержание так называемого гипотетикио-дедуктивного метода познания.

Индукция от прошлого к будущему. Эта форма вывода близка к описанной неполной индукции. Выводы этого вида могут быть выделены даже как часть рассмотренных выводов неполной индукции.

Если мы рассмотрим ряд случаев, когда в предметах сочетаются признаки S и Р и готовы сделать вывод «Все S суть Р», тогда мы готовы также заключить от какого-то наблюдаемого случая (уже подвергшегося наблюдению, положим, последнего) такого сочетания к тому, что для следующего предмета, который мы будем рассматривать, при наличии у него S, также будет Р.

Другими словами, умозаключение здесь совершается от одного случая сочетания признаков или вообще некоторого наступившего явления к тому, что оно – при соответствующих условиях – наступит и в следующий раз. Положим, мы многочисленное количество раз бросаем фишку и каждый раз при этом выпадает одно и то же число очков. Тогда мы заключаем, что и при следующем бросании выпадает то же самое число. Обобщая сказанное, видим, что это умозаключение относится к следующему типу: от одного последнего случая каких-то испытаний из множества испытаний, при которых получен один и тот же результат, мы заключаем, что следующее испытание даст тот же результат.

Кажется, и обычно так считают, что чем больше число случаев, в которых получен один и тот же результат, тем вероятнее, что и следующие испытание даст тот же результат. Однако это не всегда так. Есть две объективных возможности:

1. Когда совпадение результатов множества испытаний является случайным (например, при игре в рулетку выпадение, несколько раз подряд красного цвета – при исправности рулетки).

2. Когда появление этого результата чем-то детерминировано (например, неисправность рулетки, в силу которой выпадает красный цвет, или особенности бросаемой фишки – выпадаемая сторона ее легче противоположной).

Если имеет место первая возможность, то чем больше случаев, когда некоторое явление произошло, то тем меньше вероятность, что оно произойдет в следующий раз. Во втором же случае – наоборот. Это значит, что человеку, делающему умозаключение по этому способу неполной индукции, надо обратить внимание не только на число случаев возникновения данного явления, по думать также и о том, почему может происходить повторение одного и того же результата. Уже даже некоторое предположение об этом может помочь ему воздержаться от поспешных заключений.

 

СТАТИСТИЧЕСКИЕ ВЫВОДЫ

Статистические выводы – это умозаключения, заключения которых представляют собой утверждения о частоте наступления некоторого явления или о частоте, с которой встречается некоторый признак в пределах какого-то множества М предметов или явлений. Это множество называют в социологии генеральной совокупностью.

Примерами таких заключений может быть число выпадения дождей в какой-то период летнего времени или число морозных дней в зимний период; число заболеваний в множестве дней или лет; число голосов, которые могут быть поданы за или против кандидатов на каких-то выбора (в некоторой стране с множеством избирателей М).

Эти выводы обычно трактуют так: составляется некоторое подмножество элементов множества М таким образом, чтобы оно могло служить представителем (репрезентантом) всего множества М. Это значит, что в это подмножество отбираются предметы разных качеств из М (существенных для решения поставленной задачи) в тех же пропорциях, которые имеются в М. Это подмножество называют выборкой. Далее определяется искомая частота в выборке и результат, полученный для выборки переносится на все множество М.

В таком виде умозаключения этого типа нет оснований трактовать как индуктивные, поскольку здесь вообще нет никаких обобщений: М не является обобщением выборки!

Однако при более детальном и тщательном анализе структуры выводов этого рода они оказываются сложными выводами – сочетанием неполно-индуктивного (то есть представляют собой неполные индукции) и силлогистического (дедуктивного) вывода.

В самом деле, поставим вопрос перед тем, кто делает указанный вывод: «Был ли бы получен тот же результат, если была бы взята другая выборка, составленная по тем же принципам?» Если он уверен в правильности своего вывода, то ответ должен быть положительным. Но это означает, что он предполагает – в качестве заключения своего вывода – общее утверждение: «Для всякого подмножества из совокупности М, составленного по таким-то и таким-то принципам (которыми он пользовался при составлении своей выборки), то есть для всякого множества, подобного по своей структуре множеству М, имеет место такая-то частота (наступления явления или наличия признака)».

Это утверждение представляет собой заключение индуктивного характера вида «Все S суть Р», где S есть понятие «подмножество М, подобное выборке», обобщающее указанные подмножества, а Р – понятие «множество, имеющее частоту, наблюдаемую в выборке». Но раз это верно для любого подмножества, подобного выборке, значит верно и для самого М, поскольку М является подобным выборке по условию составления самой выборки (Здесь подразумевается еще предпосылка о симметричности отношения «подобия»: если выборка подобна множеству М, то М подобно выборке.).

Последняя часть есть вывод силлогистического вида: «Все S суть Р», «М есть S», следовательно, «М есть Р».

Таким образом, рассматриваемые статистические умозаключения, являясь сложными, включают в качестве своей главной части обобщение по принципу неполной индукции. Вторая их часть есть силлогистический (дедуктивный) вывод.

ВЫВОДЫ ПО АНАЛОГИИ

Умозаключения по аналогии играют важную эвристическую роль в научном познании, являясь одним из основных способов формирования научных гипотез. На первых этапах исследования новых, незнакомых явлении ученые обычно ищут какие-то аналоги их и используют, таким образом, уже имеющиеся знания. Подчеркивая важную роль аналогии и, по-видимому, даже несколько преувеличивая ее, И. Кеплер писал: «Более чем что-либо иное, я люблю аналогии, моих самых надежных помощников. Им доступны все секреты Природы...»

Выводы по аналогии – одна из форм правдоподобных выводов. Вряд ли будет преувеличением сказать, что это одна из наиболее распространенных форм выводов указанного типа. Основу этих выводов составляет сходство (аналогия) предметов в некоторых признаках. Два предмета аир сходны (аналогичны) в некоторых признакахP₁, ..., Р_n, если они оба обладают этими признаками (Естественно различать реальные сходства предметов от метафорических. Метафорическое сходство (метафора) является результатом отождествления заведомо не тождественных предметов (относящихся обычно к различным областям действительности) на основе некоторого их реального сходства. Это отождествление выражается в перенесении названий с одних предметов на другие и осуществляется ради того, чтобы подчеркнуть значимость одинаковых характеристик предметов. Хлопок называют «белым золотом», нефть – «черным золотом», чтобы подчеркнуть их ценность в экономической жизни страны. Признаком действительного сходства хлопка и нефти с золотом состоит именно в их ценности для народного хозяйства. Систему транспортных коммуникаций страны называют иногда ее «кровеносной системой», подчеркивая сходство роли этой системы для народного хозяйства страны с той, которую играет кровеносная система в организме. Реальные аналогии некоторые авторы называют объяснительными, а метафорические – экспрессивными аналогиями. Однако эта терминология является не вполне удачной, как и сама заключенная здесь мысль о том, чтобы якобы речь идет о двух видах аналогии в собственном смысле слова.). Само умозаключение по аналогии состоит в переходе от знания о сходстве двух предметов в некоторых признаках P₁, ..., Р_n (признаки сходства) и о наличии еще некоторого признака Q(переносимый признак) у одного из этих предметов к заключению о вероятном наличии этого последнего признака и у другого предмета. Здесь, как и во многих случаях ранее, мы употребляем слово «предмет» в широком смысле, имея в виду объекты познания вообще (возможные предметы мысли – см. § 12).

Таким образом, умозаключение по аналогии имеет следующую форму:

 

 

Из этой схемы видно, что посылки указывают на сходство предметов α и β в признаках P₁, ..., Р_n и на наличие, кроме того, признака Q у предмета α. Заключение – на вероятное наличие этого последнего признака у предмета β.

 

Пример

 

Когда-то возникло предположение о наличии жизни на Марсе (Q(β)) на основе сходства Марса (β) и Земли (α) по величине (P₁), по наличию атмосферы (Р₂)и на основе того, что обе планеты являются достаточно остывшими (Р₃) и, конечно, знания о том, что имеется жизнь на Земле (Q(α)).

Полезно выделить некоторые виды аналогии в зависимости от того, что представляют собой предметы α и β – являются ли они индивидами, последовательностями индивидов, агрегатами и т.д. и, соответственно,– в зависимости от характера рассматриваемых признаков. Так, если α и β индивиды а и b, a P₁, ..., Р_n – признаки, указывающие на наличие или отсутствие у них тех или иных свойств, то говорят об аналогии признаков или, можно было бы сказать, об аналогии свойств. Приведенный выше пример относится как раз к их числу, где а и b – индивиды: Земля и Марс.

Если α и β – некоторые последовательности предметов, соответственно – а₁, а₂, ..., а_n и b₁, b₂, ..., b_n (пары, тройки, n-ки предметов вообще), а признаки P₁, ..., Р_n, как иQ – n-местные отношения, в которых находятся члены этих последовательностей, то имеем, так называемую аналогию отношений.

Так, при n = 2 умозаключение имеет структуру:

 

 

Пример

 

Положим, мы знаем, что пары людей а₁, а₂ и b₁, b₂ сходны при наличии у них отношений:

A₁ сын а₂ (Р₁(а₁, а₂)) и а₁ заботится об а₂ (Р₂(а₁, а₂)), и соответственно, b₁ сын b₂ (P₁(b₁, b₂)), b₁ заботится о b₂ (Р₂(b₁, b₂)), а также знаем, что а₁ любит а₂ (Q₁(a₁, а₂)), тогда можем заключить: вероятно, что b₁любит b₂ (Q₁(b₁, b₂)).

Заметим, что аналогию отношений всегда можно истолковать как аналогию реляционных свойств (согласно общему принципу истолкования отношения как реляционного свойства какого-либо из объектов этого отношения – см. § 13). Все зависит от того, что мы берем в качестве субъекта в суждениях, представляющих собой посылки. В случае аналогии отношений субъектами являются пары, тройки и т. д. предметов. Если в качестве субъекта высказываний P₁(a₁, a₂), ..., P_n(a₁, a₂)) выделить а₁, тогда его отношение P₁, ..., Р_n суть его реляционное свойство. Аналогично для высказываний P₁(b₁, b₂), ..., P_n(b₁, b₂), когда в качестве субъекта их выделяется предмет b₁.

Но при таком представлении аналогии возможны фиксация сходств рассматриваемых нами предметов также и по атрибутивным свойствам, как и по таким реляционным, которые выражают отношение рассматриваемых предметов к любым другим предметам. Так, в качестве высказываний, фиксирующих сходство предметов a₁ и b₁ можем иметь, наряду с указанными, также P_n+1(a_r), P_n+2(a₁, a₂, а₃) и аналогично для b₁. Таким образом, расширяются возможности учета имеющихся сходств предметов.

Особенно полезными в научном познании являются, по-видимому, умозаключения, которые условно назовем структурными аналогиями. Специфика их состоит в том, что предметами аир являются здесь некоторые агрегаты (системы), а их признаками – характеристики их структур: состав частей, способ их соединения и т.п. Так, в развитии теории атома на некотором этапе играла роль аналогия между атомом и планетарной, в частности Солнечной, системой (планетарная модель атома). Признаки сходства здесь – наличие у того и другого массивного ядра (центральное тело) и вращающихся вокруг него тел со сравнительно небольшими – относительно самого ядра – массами. Переносимым – известным признаком – может быть наличие притяжения между центральным телом и периферийными телами планетарной системы. Правда, сразу же при этом возникла мысль о различии характера взаимодействий (гравитационных – в одном случае, и, в основном, электромагнитных – в другом случае).

В некоторых особых случаях, впрочем, весьма распространенных, в качестве агрегата правомерно рассматривать предмет, представляющий собой некоторую систему количественных характеристик: электрический ток может рассматриваться как совокупность таких определенным образом связанных между собой параметров как напряжение (зависящее от разности потенциалов на концах проводника), сила тока, сопротивление. Тогда аналогичным ему является поток жидкости, который характеризуется силой, действующей на его частицы и зависящей от разности уровней каких-то участков потока (аналог электрического напряжения), количество жидкости, протекающей через поперечное сечение за единицу времени (аналог силы тока), сопротивление движению жидкости (аналог электрическому сопротивлению). Известна связь между указанными характеристиками электрического тока (закон Ома): сила тока прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению участка цепи. Естественно предположить о наличии такой же связи между соответствующими характеристиками потока жидкости (хотя правомерен, конечно, и обратный переход – от жидкости к току).

Вполне очевидно, что рассмотренная аналогия, как впрочем и многие другие, полезна не только как основание для умозаключения, но имеет и определенное познавательное значение само по себе, например, для уяснения характеристик потока жидкости. Выявление познавательных аналогий играет важную роль в научной практике для разъяснения абстрактных, недоступных непосредственному восприятию явлений, способствуя их уяснению и пониманию.

К указанному виду структурных аналогий относится широко известное, так называемое физическое моделирование. Делая заключение, например, о том, как будет вести себя строящийся самолет, судно, плотина, на основе поведения соответствующей модели, учитывают обычно структурное сходство их и в смысле строения, и в смысле количественных характеристик.

Каждый мог заметить, насколько широко используется метод структурных аналогий в процессе овладения языком – при определении правил произношения слов, ударений и т.д. Зная, например, что в слове «потолок» ударение падает на последний слог, мы можем заключить, что так же должно обстоять дело со словом «каталог», которое структурно сходно с первым. Одинаковое ударение, очевидно, должны иметь структурно сходные слова «договор», «приговор», «уговор», «доценты» и «проценты» и т.п. Хотя нельзя и абсолютизировать этот метод – мы скажем, например: «В этой библиотеке нет потолка». Как по аналогии сказать в этой ситуации об отсутствии в ней каталога?

В криминалистической практике – как хорошо известно, по крайней мере, любителям детективов – постоянно употребляется понятие «почерк преступника», то есть структурная характеристика способа совершения преступлений определенного типа некоторым лицом. На основе этих сходств нередко выявляется сам преступник.

Особым видом структурной аналогии можно считать аналогию рассуждений (умозаключений), в которых некоторые утверждения относятся к сходным ситуациям. Аналогии этого типа используются как способ опровержения некоторых рассуждений: на основе сомнительности или явной несостоятельности утверждения, относящегося к одной ситуации, делается заключение о несостоятельности его в применении к другой.

Если кто-то рассуждает таким образом: «Поскольку все преступления уголовно наказуемы и всякий грабеж тоже уголовно наказуем, следовательно, всякий грабеж – преступление», то вместо того, чтобы разъяснять человеку неправильность этого рассуждения ссылками на нарушение правил силлогизма (Нераспределенность среднего термина в обеих посылках или неправильный вывод по второй фигуре с двумя утвердительными посылками.), можно привести рассуждение такой же – аналогичной – логической структуры применительно к другой ситуации, в которой выявляется его явная абсурдность:

 

 

Итак, умозаключение по аналогии позволяет получить новое знание лишь с большей или меньшей степенью вероятности того, что оно соответствует действительности. Есть, однако, определенные условия, которые позволяют повысить эту степень вероятности, то есть делать наши выводы более правдоподобными.

Во-первых, ясно, что вывод по аналогии тем правдоподобнее, чем больше сходств между предметами при этом учитывается. Однако сразу надо сказать, что отнюдь не любые сходства «идут в дело». Никто не стал бы делать выводы о наличии жизни на какой-то планете в силу того лишь, что она, как и Земля, шарообразна, вращается вокруг своей оси, а также вокруг Солнца. Каждые два человека сходны во множестве признаков, но не любое множество сходств позволяет, например, заключить об одинаковости их профессии, увлечений и т.д. Из того, что оба человека брюнеты, худощавы, темпераментны и один из них – бизнесмен, явно не следует, что и другой занимается тем же самым.

Таким образом, мы приходим ко второму условию повышения степени правдоподобия: в качестве основы вывода необходимо установление сходств предметов в таких признаках P₁, ..., Р_n, которые, по крайней мере предположительно, связаны тем или иным образом с переносимым признаком Q, в какой-то мере детерминируют (обусловливают) его, то есть являются в какой-то мере существенным для него.

Это требование не является, конечно, формальным и выполнение его, как и вообще большая или меньшая эффективность использования метода аналогий, зависит от уровня знаний человека. Чем ниже уровень, тем больше у него склонность к поверхностным, явно несостоятельным аналогиям.

Отмечают иногда, что заключения по аналогии могут быть даже достоверными и называют такие аналогии полными или строгими. Такое возможно в том, например, случае, когда известно, что какие-то признаки сходства однозначно детерминируют переносимый признак. Если установлен, например, ряд сходств между льдом и железом, в числе которых, наряду с другими, фигурирует кристалличность того и другого, тогда перенос знания о наличии определенной температуры плавления от льда к железу в принципе имеет достоверный характер, поскольку уже сам признак кристалличности какого-то вещества детерминирует у него определенную точку плавления.

Однако, если указанная связь (детерминированность) между признаками уже известна, тогда вывод, по существу, превращается в дедуктивный: знание о том, что кристалличность вещества детерминирует наличие у него определенной температуры плавления означает, что имеется общее высказывание «Всякое кристаллическое вещество имеет определенную температуру плавления». Добавление к этому утверждения «Железо кристаллично» приводит к обычному силлогизму с заключением «Железо имеет определенную температуру плавления» – аналогия железа со льдом оказывается пои этом вообще излишней!

Для повышения степени правдоподобия выводов по аналогии весьма полезно также учитывать, наряду со сходствами предметов, их различие. Нередки случаи, когда одно какое-то различие указывает на неправомерность аналогии, несмотря на все множество сходств. Нетрудно указать множество сходных признаков между Землей и Луной, однако отсутствие у Луны атмосферы делает неправомерной попытку сделать заключение о наличии на ней жизни на основе аналогии с Землей.

Вывод по аналогии без учета хотя бы уже известных различий между соответствующими предметами нельзя даже считать логически корректным. Теологи в опровержение рассуждений атеистов о том, что допущение Богом зла в мире свидетельствует о том, что Он не является, по крайней мере, всеблагостивым, как его характеризуют, приводят следующую аналогию. Бог подобно хирургу, причиняющему больному боль, оперируя его, невиновен в ней. Он так же, как и хирург, допускает зло, бедствия человечества и связанную с ними боль для излечения болезней и потому невиновен в ней, как и хирург. Однако в этом рассуждении по аналогии не учитывается весьма важное, как кажется, различие: болезнь возникает у больного не по воле хирурга, тогда как болезни и страдания человечества не могут возникнуть помимо воли Бога – согласно верованиям самих же теологов.

Наконец, для иллюстрации того, как важно в аналогиях не упускать из вида различия, напомним известную и поучительную историю с ослом. Когда он вез на своем горбу мешки с сахаром, то, переходя вброд реку, почувствовал большое облегчение. Руководствуясь аналогией, он предвидел то же самое, когда в другой раз переходил ту же реку с грузом хлопка того же веса. В результате, как догадывается читатель, у нашего героя возникли сильные сомнения относительно ценности выводов по аналогии!

Несмотря на сказанное выше о роли выводов по аналогии, надо заметить, что эти выводы по своей форме не представляют сбой отношение индуктивною следования между посылками и заключением. Иначе говоря, заключенных Р_n (β) не является индуктивным следствием посылок, что можно проверить, пользуясь указанным выше табличным способом (см. «Индуктивное следование»). Очевидно, это указывает на необходимость уточнения формы выводов по аналогии. Возникает предположение, что при употреблении выводов по аналогии в практике научного познания, при котором они представляются как действительно правдоподобные выводы, неосознанным образом употребляются какие-то дополнительные посылки, и задача состоит в выявлении таковых.

 

НЕКОТОРЫЕ МЕТОДЫ НАУЧНОГО ПОЗНАНИЯ

По существу, о некоторых методах (приемах, способах) решения тех или иных задач познавательной деятельности мы говорили уже в предыдущих разделах. Таковыми являются рассмотренные выше операции с понятиями: деление, обобщение, ограничение понятий. Тем более к ним относится прием определения. Рассматривая индукцию мы отмечали, что она интересует нас в первую очередь не как форма вывода, а как способ получения общего знания. Однако мы не выделяли эти способы познания отдельно, считая целесообразным связать их с формами мысли, каковыми являются понятие, суждение, а также с такими формами мышления, как дедуктивные умозаключения. В связи с последними была рассмотрена важная форма подтверждения гипотез, которую можно так и охарактеризовать – «подтверждение посредством дедуктивных умозаключений».

Что касается последних, то они, с одной стороны, связаны с суждениями, поскольку представляют собой определенного типа операции с суждениями (способы выведения одних суждений из других). В логике их нередко характеризуют вообще как процессы преобразования суждений. С другой стороны, они являются, конечно, также и определенными методами познания – методами получения нового знания на основе имеющегося. При этом нет надобности специально говорить о большой значимости этих методов, поскольку при помощи умозаключений мы познаем нередко то, что недоступно чувственному восприятию. К этому надо добавить еще и то, что они представляют логику рассуждений в собственном смысле слова и потому составляют в истории логики основной предмет ее изучения.

В этой же главе речь пойдет о некоторых специальных методах научного познания. Конечно, ставить здесь задачу рассмотрения всех методов научного познания невозможно. Тем более, что некоторые из них не связаны с логикой. Здесь же мы рассматриваем лишь те, что имеют такую связь, в описании которых существенное значение придается использованию определенных понятий и положений логики, в особенности – понятия логического следования, а вместе с ним и понятия умозаключения.

В связи с намеченным уже ранее различением эмпирического и теоретического уровней познания (см. §§ 1, 12) естественно различение методов эмпирического и методов теоретического познания.

К числу эмпирических методов познания относятся методы наблюдения, анализа, обобщения (Общая характеристика этих методов дана в § 1. Они же, с теми или иными модификациями, применяются и на теоретическом уровне познания.) наблюдаемых явлений, посредством которых наука приобретает исходный фактический материал для проникновения в сущность явлений и установления законов связи между ними. Здесь будут рассмотрены эмпирические методы установления причинной зависимости явлений.

Среди методов теоретического познания (рассматриваются далее – в разделе «Теория и некоторые методы теоретического познания») – метод научного объяснения и гипотетико-дедуктивный метод познания. В этом же разделе – в той мере, в какой это здесь возможно – такие понятия, как вопрос и гипотеза, поскольку они играют важную роль в теоретической деятельности. Кроме того, в последней главе рассматриваются методы доказательства и опровержения, так же относящиеся к числу теоретических методов познания.

Поскольку речь здесь зашла о делении методов познания на теоретические и эмпирические, естественно вспомнить и о тех методах, которые были рассмотрены выше. Операции с понятиями применяются как на эмпирическом, так и на теоретическом уровнях познания – в зависимости от характера самих понятий. Умозаключения,– прежде всего дедуктивные – поскольку они, наряду с другими приемами творческой деятельности мышления, приводят к новому знанию, являются типичными теоретическими способами познания. Правдоподобные выводы (аналогия, индукция) – это, скорее всего, переходные формы от эмпирического к теоретическому познанию.

 

ЭМПИРИЧЕСКИЕ МЕТОДЫ ОБОСНОВАНИЯ ИНДУКТИВНЫХ ОБОБЩЕНИЙ

Выше мы рассмотрели один из методов эмпирического познания, каковым является индукция. Она, с одной стороны, включает некоторые формы правдоподобных выводов, но наиболее существенная ее характеристика, как мы уже отмечали, состоит в том, что в ее лице мы имеем методы получения общего знания. Иначе говоря, результатами индуктивных выводов являются более или менее правдоподобные высказывания общего характера. Будучи, как правило, проблематичными, эти высказывания требуют дополнительных обоснований. И наиболее важным способом такого обоснования является выяснение причин обобщаемых явлений. Не случайно поэтому в истории логики возникло специальное учение о методах выявления причинной зависимости явлений. Основоположник его – Ф. Бэкон – придавал ему настолько важное значение, что – в противоположность учению Аристотеля, то есть его «Органону» – назвал свое учение «Новый Органон».

По мысли Ф. Бэкона, в этом его учении заключены основные методы научного познания, позволяющие выявлять сущность и законы явлений. Однако значение данной теории, как можно видеть в свете современной эпистемологии, является, конечно, более скромным. Хотя бы потому, что речь идет лишь о способах эмпирического познания. Хотя выявление причин тех или иных явлений весьма существенно для понимания явлений и управляющих ими законов, но отнюдь неправильно понимать это как некий завершающий этап познания. Остается актуальной еще задача выяснения того, каков механизм действия этой причины, что относится уже к теоретической ступени познания (см. § 43).

Отметим еще, что рассматриваемые в этой главе методы явились результатом дальнейшего совершенствования теории Ф. Бэкона в трудах ряда логиков философского направления: Д. Гершеля, особенно Дж. Ст. Милля и других. В результате в современной литературе они получили названия «методы Бэкона-Милля».

Строго говоря, методы предназначены для выяснения опытным путем – посредством наблюдений или экспериментов – не только причин, но и вообще обстоятельств, причинно связанных с некоторым явлением. Под термином «явление» понимается при этом возникновение или исчезновение чего-либо: сверкнула молния, пошел дождь, выздоровел человек, произошла катастрофа – все это явления. К числу причинно связанных с некоторым явлением обстоятельств относятся: причина его, необходимые условия действия этой причины, а также обстоятельства, которые, за неимением лучшего термина, будем называть «не необходимыми релевантными сопутствующими обстоятельствами» или даже просто: релевантно сопутствующими этому явлению.

Данные методы могут служить также для выяснения наличия или отсутствия необходимой связи между признаками S и Р в высказываниях вида «Все S суть Р», получаемых в индуктивных умозаключениях.

Что касается причинных зависимостей, то здесь мы ограничимся задачами выяснения причин и необходимых условий некоторого явления и, возможно, релевантно сопутствующих обстоятельств. Задача выявления следствий некоторого явления не столь актуальна и к тому же решается аналогичным образом.

 Понятие причины и основные свойства причинных связей

В мире нет изолированных, обособленных явлений. Как в природе, так и в обществе явления связаны друг с другом, зависят друг от друга и обусловливают друг друга. Взаимосвязь и взаимозависимость явлений, взаимодействие между ними являются объективной закономерностью развивающегося материального мира.

Изучая явления природы и общества, мы должны брать их такими, каковы они есть в действительности, то есть в их взаимосвязи. Рассмотрение явлений в их взаимной связи и взаимозависимости является необходимым условием научного исследования природы, познания ее закономерностей.

В процессе познания природы и общества различные науки изучают различные формы и стороны взаимосвязи предметов, явлений действительности. Математика исследует количественные и пространственные отношения тел. Химия изучает законы связи между химическими элементами. В общественных науках – политической экономии, праве, истории и т.д.– изучаются экономические, политические связи, отношения между людьми, классами, государствами. В логике – законы связи мыслей в процессе рассуждения и т.д.

Среди различных форм связи и взаимозависимости явлений природы и общества одно из важнейших мест занимает причинная связь явлений. Поэтому на методах определения причинной зависимости между явлениями в логике останавливаются специально.

• Под причинной, или каузальной (от латинского слова causa – «причина»), связью понимается связь причины и Действия (следствия). Состоит эта связь в том, что каждое явление природы и общества обязательно вызывается каким-либо другим явлением или явлениями. Находясь во всеобщей связи, всякое явление непременно обусловлено другими явлениями.

Причиной называется явление или совокупность явлений, которые предшествуют другому явлению и вызывают его. Например, нагревание жидкости увеличивает ее испарение. Нагревание жидкости в данном случае является причиной увеличения испарения, так как оно предшествует второму явлению и вызывает его. Следствием (действием) называется то явление, которое следует за другим явлением и вызывается им. Увеличение испарения является в нашем примере следствием, ибо оно следует за нагреванием жидкости и является его результатом. Знание причин дает возможность научно объяснить явления действительности, познавать их закономерности и благодаря этому предвидеть наступление явлений. Знание причинной связи позволяет также управлять явлениями в соответствии с потребностями людей. Изучив причины, мы можем предотвращать наступление нежелательных явлений и вызывать такие, которые полезны людям в их жизни.

Однако каждая причина действует при наличии некоторых условий, называемых необходимыми условиями действия причины. Для того чтобы, например, состоялось испарение воды кроме нагревания (причины) необходимо, конечно, по крайней мере, наличие источника нагревания и какого-то пространства, в которое происходит испарение. Для вспышки спички при трении ее о спичечную коробку (причины) необходимо наличие кислорода в окружающем пространстве, а также исправность коробки и того, чтобы и коробка, и спички не были отсыревшими.

Наличие причины и всех необходимых условий ее действия в совокупности составляют достаточное условие для наступления явления. Наличие же самой причины и каждого необходимого условия ее действия является необходимым условием появления явления, то есть если нет хотя бы одного из указанных обстоятельств, то нет и явления. Таким образом различаем: необходимые условия действия некоторой причины и необходимые условия наступления некоторого явления.

Как обычно бывает, особенно когда речь идет о сложных и тем более абстрактных объектах, грани между различными их видами не являются всегда определенными. Так обстоит дело и с различием причин и необходимых условий. Обычно понятие причины связывают с таким признаком, как активность обстоятельства, его способность вызывать какие-то действия.

По-видимому, в наиболее широком смысле причиной некоторого явления естественно называть то обстоятельство, которое позволяет объяснить, почему и как Появляется данное явление, хотя при этом сохраняется такая характеристика причины, что она предшествует своему действию во времени. Например, естественно назвать причиной того, что некоторые вещества имеют определенную температуру плавления, такой их общий признак, как кристалличность, поскольку именно кристалличность объясняет указанную специфику упомянутых веществ. И здесь подразумевается определенный временной процесс проявления кристалличности: наличие определенной температуры плавления означает, что при нагревании кристаллического вещества, находящегося в твердом состоянии, температура его повышается до определенного уровня и затем останавливается до перехода вещества в жидкое состояние, по существу,– до разрушения кристаллической структуры.

Релевантно сопутствующие обстоятельства – это обстоятельства, которые не являются необходимыми для действия данной причины, но так или иначе влияют на ее действие, то есть ускоряют действие причины либо, наоборот, ослабляют ее действие, увеличивают или уменьшают интенсивность этого действия, что, конечно, отражается и на результате (на самом явлении, которое вызывает эта причина). В случае с испарением воды это, например, величина внешнего давления на жидкость, подвергаемую нагреванию.

Причиной гриппа, как известно, является действие определенного вируса. Обстоятельствами, ослабляющими его действие, выступают закалка организма, качественное питание, активный образ жизни, а ослабляющими – истощение организма, отсутствие витаминов и т.п.

Еще пример. Мы нередко наблюдаем, что то или иное лекарство при одних и тех же обстоятельствах действует более или менее эффективно или быстро в зависимости от того, запивают ли его теплой или холодной водой, размельчают таблетку или нет, принимают до или после еды и т.п. Обычно упомянутые обстоятельства не являются необходимыми условиями соответствующего действия лекарства, но, с другой стороны, не являются и безразличными к этому действию. Знание обстоятельств такого рода является во многих случаях весьма важным.

Причина, необходимое условие и релевантно сопутствующие обстоятельства – это все, конечно, обстоятельства релевантные данному явлению. Релевантно сопутствующие обстоятельства выделяются в этом смысле как один из видов таковых.

Причинная связь является всеобщей. Она присуща всем без исключения явлениям природы и общества. Ни в природе, ни в обществе нет явлений, которые бы не вызывались определенной причиной. Ничто не происходит без причины. Все явления природы и общества детерминированы, то есть причинно обусловлены.

Причинная связь есть необходимая связь. Понятие необходимой связи не следует смешивать с понятием необходимых условий чего-либо. Причинная связь необходима, но не всякая необходимая связь является причинной.

Когда присутствует причина и необходимые условия ее проявления, то обязательно происходит действие; когда есть действие, то непременно имеет место и его причина. Причина и действие неразрывны, они существуют только в единстве. Иначе говоря, необходимая связь между явлениями означает однозначную детерминированность, обусловленность одного другим. Примерами необходимой, но не причинной связи между явлениями могут служить связь между делимостью суммы цифр числа на 3 и делимостью самого числа на 3, связь между параллельностью противоположных сторон четырехугольника и равенством этих – параллельных – сторон и др.

Если при изучении того или иного явления, играющего роль причины, мы не обнаруживаем производимого им действия, то это не означает отсутствие действия вообще. Действие существует, но оно либо еще не распознано среди других явлений, либо уничтожено обратным действием другой причины. Точно так же, если мы наблюдаем какое-либо явление и не замечаем его причины, это означает только то, что причина еще не найдена нами.

Причинная связь обладает свойством определенности и однозначности. Определенная причина производит вполне определенное действие, причем одинаковые причины, действующие в разное время, в разных местах, при одних и тех же условиях вызывают одинаковые действия, хотя одно и то же явление может быть результатом действия разных причин (принцип множественности причин) или одной и той же причины при разных условиях ее действия. Хотя, опять-таки, наряду с множественностью причин существуют, конечно, и такие случаи, когда явления вызываются только одной единственной причиной. Например, каждое из следующих явлений: затмение Солнца или Луны, смена дня и ночи и времен года, морские приливы и отливы, заболевание малярией – и многие другие явления происходят всегда от одной и той же, особой для каждого из этих явлений, причины. К этому добавим, что представление о множественности причин нередко возникает в силу того, что не различают непосредственно наблюдаемые и непосредственно действующие, вызывающие явление. Во врачебно-криминальной практике причиной смерти человека в одних случаях считают удар тяжелым предметом по голове, в других – удар человека головой об пол, стену при падении. Однако ближайшая, непосредственно вызывающая смерть человека причина и в том, и в другом случае одна – нарушение жизненно важных функций головного мозга. Но она не относится к числу наблюдаемых обстоятельств и поэтому не может быть обнаружена посредством описываемых ниже методов эмпирического исследования.

Причина и действие последовательны во времени, то есть причина всегда предшествует действию, а действие всегда следует за причиной, во всяком случае не может опережать ее.

Из последовательности причины и действия во времени следует, что причину всякого явления необходимо искать среди предшествующих ему явлений. Явление, происшедшее после данного явления, не может быть его причиной.

Последовательность причины и действия во времени составляет один из важнейших, но не единственный признак причинной связи. Одного этого признака недостаточно для распознания причинной связи. Поэтому если мы наблюдаем последовательную смену двух явлений, то на основании одного этого признака мы не можем делать вывод об их причинной связи. Одно явление может постоянно предшествовать другому, не находясь с ним в причинной связи. Весна, например, всегда предшествует лету, но не является его причиной.

Отождествление последовательности явлений во времени с причинной связью является источником логической ошибки, носящей латинское название post hoc ergopropter hoc (после этого – значит по причине этого). Ошибка такого рода чаще всего допускается суеверными людьми. Например, в 1811 г. появилась большая блестящая комета. Необыкновенный в сравнении с другими небесными телами вид кометы и быстрые перемещения ее по небу вызвали суеверный страх. Появление ее было истолковано как предзнаменование большого несчастья. Вскоре, в 1812 г., Наполеон вторгся в Россию. Эти два события были поставлены суеверными людьми в причинную связь. В действительности же никакой связи, кроме случайно совпавшей хронологической последовательности, между этими явлениями не было. Точно так же суеверные люди долгое время связывали молебствие и следовавшее иногда за ним появление дождя, черную кошку, перебежавшую дорогу, и несчастье и т.д. Но это – предрассудки, которые ничего общего не имеют с наукой. Причинное объяснение явлений – противник житейских предрассудков.

Было время, когда наука носила чисто описательный характер. Она констатировала факты, но не объясняла их, не интересовалась или мало интересовалась вопросом, почему эти факты имеют место. Астрономия вплоть до XVII в. занималась в основном описанием форм движения небесных светил, механика – классификацией и описанием движения тел (кинематикой тел), биология – описанием животных и растительных организмов и т.д.

Для научного объяснения явлений мира, для целесообразной деятельности человека одного описания недостаточно. Например, на основании описания болезни нельзя сказать, почему она возникает и как ее лечить, в каких случаях можно ожидать и как предотвратить. Для того чтобы объяснить происхождение той или иной болезни и эффективно бороться с ней, необходимо знать причины, которые вызывают ее. Наука, таким образом, не может ограничиться только описанием явлений.

У различных явлений природы и общества характер причинной зависимости различен. Иначе говоря, формы причинной связи в мире многообразны. Поэтому связь причины и действия гораздо сложнее, чем это может показаться на первый взгляд. В связи с этим установление причинной зависимости явлений, то есть определение причины и ее действия, представляет собой нелегкую задачу.

Трудности установления причинной связи обусловливаются целым рядом обстоятельств.

Во-первых, каждому явлению предшествует бесконечное множество других явлений. Выделить причину среди этого многообразия явлений – сложная задача.

Во-вторых, причина и действие, как и все явления, не изолированы, не отгорожены друг от друга, а взаимосвязаны и взаимозависимы. При этом активна не только причина, но и действие. Если причина вызывает, порождает действие, то и действие нередко влияет на причину.

В-третьих, установить причину явления в случае множественности причин сложнее, чем в том случае, когда явление вызывается только одной причиной. При множественности причин каждый раз нужно выяснять, какой из возможных причин вызвано явление. А это делает задачу определения причинной связи более трудной.

Наконец, определение причинной связи очень усложняется явлением смешения действий разных причин. Происходит это в тех случаях, когда исследуемое явление представляет собой результат совместного действия двух и более причин. В таких случаях общая причина является составной, сложной. Составным является так же и действие этих причин, так как каждая из причин вызывает свое действие, а сложение их дает то явление, которое изучается.

Например, нагревание якоря электромотора происходит за счет электрического тока, проходящего по его обмотке, за счет паразитных токов (токи Фуко), возникающих в металлических частях якоря, и за счет трения якоря в подшипниках.

Сложение действий нескольких совместно действующих причин в одно общее, результирующее явление и носит название смешения действий.

В зависимости от характера причинной связи смешение действий происходит двояким образом. В одних случаях действия просто накладываются одно на другое, изменяя лишь количество общего действия, увеличивая или уменьшая его. Так, в вышеприведенном примере с нагреванием якоря электромотора действия всех трех причин складывались. При испарении жидкости повышение температуры жидкости и увеличение давления над нею ослабляют друг друга, так как повышение температуры увеличивает испарение жидкости, а повышение давления уменьшает испарение жидкости.

Возможно также, что действие одной причины погашает действие другой. Например, согласно известному закону механики, действие силы на некоторое тело создает ускорение его движения (или выводит его из равновесия). Однако, давя рукой на стену, мы не обнаруживаем ее ускорения. Все дело в том, что противодействие стены создает такое же по величине ускорение, что и действие нашей руки, но направленное в противоположную сторону.

Простое наложение действий происходит в тех случаях, когда причины дают, в основном, качественно однородные и лишь количественно различные действия. Общий результат совместного действия причин в таких случаях представляет собой количественную сумму действий отдельных причин.

При простом наложении действий каждая из причин допускает изолирование без нарушения действия остальных причин. Благодаря этому, определение причины по действию или действия по причине в таких случаях обычно не представляет большой трудности.

В других случаях сложение причин происходит таким образом, что изменяются не только количественные характеристики общего действия по сравнению с действиями отдельных причин, но и его качество. Происходит это потому, что каждая из совместно действующих причин дает качественно различные результаты, и, взаимодействуя между собой, все причины дают такое явление, которое не может быть представлено как простая сумма составляющих – действий отдельных причин. Например, составляющие солнечного спектра вызывают у нас ощущение или красного, или желтого, или зеленого и т.д. цвета. Все же вместе они создают ощущение белого цвета.

Процесс установления причинной связи во втором случае смешения действий гораздо сложнее, чем в первом, и требует учета и всестороннего анализа всех совместно действующих обстоятельств явления. Сложности указанного вида обусловливают случаи недостоверности результатов применения описываемых здесь методов.

Во всех рассматриваемых ниже методах, кроме так называемого метода остатков, по существу, выпадающего из числа методов опытного познания, в качестве исходных для получения нужных выводов используются некоторые эмпирические данные. Прежде всего некоторый – базисный – случай, имеющий место в действительности. Именно случай наступления некоторого явления и связанные с ним данные относительно того, какие обстоятельства ему предшествуют. Затем этот случай сравнивается с другими случаями наступления, отсутствия или того или иного изменения данного явления. Различие методов обусловлено прежде всего различием именно этих данных.

В применении всех описываемых ниже методов предполагается, что мы имеем уже какие-то знания, которые используются при отборе обстоятельств, предшествующих исследуемому явлению и возможно сопутствующих ему (далее будем говорить для краткости только о предшествующих обстоятельствах), и эти знания позволяют при этом выделять лишь возможно релевантные (уместные) ему обстоятельства, отбрасывая все, что явно не связано с ним причинным образом, то есть позволяют исключить все то, что явно не может влиять на это явление. Если мы хотим установить причину отравления человека, то, конечно, должны игнорировать то, что вчера у какого-то из членов какого-то парламента был насморк, что какая-то кошка осталась ненакормленной и даже то, например, что незадолго до отравления человек играл в волейбол, смотрел телевизор и т.п.

Методы установления причинной зависимости явлений

МЕТОД СХОДСТВА

Для установления причины некоторого явления а и необходимых условий ее действия при помощи метода сходства надо найти – посредством наблюдения или создать экспериментально,– по крайней мере, два случая следующего вида:

А. В₁, ...., В_n – а

А, С₁,..... С_n – а, где n ≥ 0.

Обстоятельство А может представлять собой в свою очередь совокупность обстоятельств А₁, ..., А_т (т ≥ 1). Это именно все те обстоятельства, которые являются общими среди предшествующих в обоих случаях.

Обстоятельства С₁, ..., С_n отличаются от обстоятельств B₁, ..., В_n, то есть эти множества не содержат общих элементов. Допущение n = 0 предполагает возможность некоторых вырожденных случаев. Ясно, что в любых случаях наступления а среди предшествующих ему обстоятельств всегда будет находиться не только причина, но и все необходимые условия ее действия. Итак, А является единственно сходным обстоятельством или совокупностью обстоятельств среди предшествующих и в каждом случае наступает явление а. Это дает основание с той или иной степенью вероятности заключить, что А содержит причину и все необходимые условия явления а. В качестве основы этого вывода формулируют следующее правило – специальное правило метода сходства:

• Если два или более случаев наступления исследуемого явления имеют общим лишь некоторую совокупность обстоятельств, возможно, одноэлементную, то эта совокупность обстоятельств, в которой только и сходны все эти случаи, содержит в себе причину рассматриваемого явления и все необходимые условия ее действия.

Во всех случаях, когда имеется механическое взаимодействие тел (трение тел, удары по металлу, обтачивание или распиливание бревна и т. п.), всегда возникает нагревание тел, то есть появляется теплота. Легко отобрать пары случаев, которые различаются во всех обстоятельствах, кроме указанного механического взаимодействия; это приводит к мысли, что причиной появления теплоты в случаях описанного типа является механическое взаимодействие тел.

Ученые изучали случаи возникновения рака легких у людей. Причем таким образом выбирали людей, что они попарно различались: образом и условиями жизни, характером употребляемой пищи – вообще во всех обстоятельствах, кроме того, что все они являются заядлыми курильщиками. Отсюда делается вывод, что в определенных случаях курение – является причиной этого заболевания.

Умозаключения по методу сходства довольно широко применяются в науке и в повседневной жизни. Для установления причинной связи явлений методом сходства пользуются в физике, химии, медицине, биологии и т.д. С помощью этого метода в различных науках найдены причины весьма многих явлений, например, причина радуги, причина однотипности степных растений и т.д.

Но чаще всего его эвристическая роль в процессе познания состоит в том, что он дает эмпирические данные для выдвижения гипотез о причинах тех или иных явлений.

К сожалению, заключение этого, как и других рассматриваемых методов, не является достоверным. Оно лишь в той или иной степени правдоподобно. Причинами ошибочности здесь, как и в других методах, может служить неполнота учета предшествующих обстоятельств, упущение из вида какого-либо другого сходного – наряду с выделенными – обстоятельства. Но для этого метода есть еще особое объективное обстоятельство, которое делает его менее надежным, чем другие. Это – множественность причин.

При исследовании, например, явления пищевого отравления или вообще какого-то заболевания, связанного с употреблением пищи, в одном случае причиной его могло быть употребление молока от какой-то коровы, а во втором случае – мяса этой же, забитой позже коровы. Или, положим, один из людей, подвергнувшихся отравлению, пил молоко и ел несвежие яйца. Второй также пил молоко и ел испорченное мясо; по методу сходства, в данной его трактовке, мы должны были бы заключить, что причиной отравления этих людей является употребление молока, хотя ясно, что в действительности скорее должно было бы быть так, что один отравился по причине употребления несвежих яиц, а второй – несвежего мяса.

Когда учитываются не все обстоятельства, возможны даже и такие курьезные случаи, которые высмеиваются в книге «Физики шутят», вроде того, что причиной всех смертей и даже всех бедствий людей является употребление ими в пищу хлеба, поскольку именно оно является общим обстоятельством в самых различных случаях.

Метод сходства чаще всего применяется лишь на первых ступенях исследования, для получения предположительных выводов о причинах исследуемых явлений. Эти предположения затем проверяются и обосновываются либо с помощью других знаний об исследуемых явлениях, либо посредством других, более точных методов установления причинной зависимости.

Метод сходства является по преимуществу методом наблюдения, а не эксперимента. Объясняется это, во-первых, тем, что экспериментальное воспроизведение явлений требует хотя бы предположительного знания причины, в то время, как это предположительное знание как раз и выводится обычно посредством метода сходства; во-вторых, тем, что в процессе экспериментирования, как правило, имеется возможность применять другие, более сильные методы установления причинной связи, которые будут рассмотрены ниже.

Практически метод сходства применяется (или может полезно применяться) в несколько этапов. В двух сравниваемых случаях мы можем иметь не одно сходное обстоятельство, а несколько сходных обстоятельств, положим А₁ и А₂. Тогда ищем случай, где А₂ (или A₁) отсутствует, то есть заменено каким-то другим качественно отличным обстоятельством (про которое нельзя сказать, что оно есть А₂ (соответственно, А₁). Если при этом явление а сохраняется, то мы получаем условие метода сходства в чистом его виде – второе обстоятельство (А₂ или А₁) элиминируется как не являющееся причиной.

 

МЕТОД РАЗЛИЧИЯ

При выделении обстоятельств, предшествующих некоторому исследуемому явлению а, в число их могут попадать случайные обстоятельства, фактически причинно не связанные с а. Поэтому возникает обычно необходимость какой-то проверки их для того, чтобы выделить действительно причинно связанные с явлением а обстоятельства. Решение этой задачи наиболее эффективным образом достигается по методу различия. Так, выделяя в качестве проверяемого среди предшествующих обстоятельств базисного случая какое-то обстоятельство В, то есть представляя этот случай в виде:

 

 

Таким образом, второй случай указывает на то, что среди предшествующих обстоятельств имеются все те же, что и в первом случае, кроме В_i, и отсутствует явлениеа. Это дает основание заключить, что В_i является причиной или необходимым условием а.

• Итак, специальное правило метода различия таково: Если случай, в котором исследуемое явление наступает, и случай, в котором оно не наступает, сходы между собой во всех обстоятельствах, кроме одного, то это обстоятельство, в котором только и разнятся эти два случая, есть причина или одно из необходимых условий действия причины исследуемого явлений.

Положим, задача состоит в определении причины или необходимых условий образования хлорофилла в растениях. Пусть а – «наличие нормального зеленого цвета у растения», выросшего при нормальных условиях: при нормальном освещении (B₁), нормальной смеси газов (B₂), при наличии достаточных тепла (В₃) влаги (B₄), на почве определенного характера (В₅). Данные для второй посылки  могут быть получены экспериментально. Пусть растение выражено в том же месте при всех тех же условиях, кроме B₁, a именно при недостаточном освещении. Отсюда следует заключение, что B₁ является причиной или необходимым условием а.

Другой пример, который мы даем без детального анализа, предлагая читателю осуществить его самостоятельно.

На звероферме, расположенной в лесу, невдалеке от западногерманского города Хагена, выращивали норок, колонков, куниц и серебристо-черных лис. Звероферма процветала. Однако с некоторых пор дела пошли хуже: зверьки похудели, стали вялыми, некоторые даже погибли. Разгадка была найдена при обследовании окрестностей зверофермы: в полукилометре от нее расположился молодежный центр отдыха. Там длительное время, 1-3 часа ежедневно, а по субботам и воскресеньям 5-6 часов, грохотала поп-музыка, многократно усиленная электронной аппаратурой. После ликвидации источника шума обитатели зверофермы за три недели вновь обрели былую «форму».

Из всех методов установления причинной зависимости явлений метод различия является наиболее эффективным.

В отличие от метода сходства, который представляет собой по преимуществу метод наблюдения, метод различия связан главным образом с экспериментом. Явления природы происходят обычно при столь разнообразных обстоятельствах, что два случая, сходные во всех обстоятельствах, кроме одного, в естественных условиях встречаются редко. Это и ограничивает применение метода различия при простом наблюдении явлений. В эксперименте же получить условия, которые необходимы для умозаключения по методу различия, довольно просто, так как обычно экспериментатор имеет полную возможность устранять из хода процесса отдельные обстоятельства, не изменяя остальных.

При изучении явления не всегда бывают известны все его предшествующие обстоятельства. Метод различия позволяет в ряде случаев обнаружить наличие еще неизвестных обстоятельств, находившихся в причинной зависимости с исследуемым явлением.

Например, до 80-х годов XIX века существовало упрощенное представление о пищевых потребностях животного организма. Ученые Англии, Франции и Германии утверждали, что организм нуждается только в белке и небольших количествах разных солей. В 1880 г. русский доктор Н.И. Лунин решил проверить эти утверждения. Он взял несколько десятков мышей и разделил их на подопытных и контрольных. Первых он стал кормить искусственным молоком, изготовленным из очищенных веществ, входящих в состав натурального молока,– белка, жира, казеина, сахара и соответствующих солей; других мышей, контрольных,– натуральным молоком. Подопытные мыши заболевали и гибли, контрольные оставались здоровыми. На основании этого Н.И. Лунин сделал вывод, что в естественной пище присутствуют в малых количествах неизвестные еще вещества, которые необходимы для организма. Своими опытами, проведенными по методу различия, Н.И. Лунин положил начало учению о витаминах.

Метод различия по сравнению с методом сходства имеет ряд преимуществ, которые делают его умозаключения более ценными в научной и практической деятельности человека.

Во-первых, метод различения связан главным образом с экспериментом, в то время, как метод сходства базируется, в основном, на наблюдении. Эксперимент позволяет искусственно изменять условия явлений, поэтому метод различия оказывается более удобным и более простым приемом исследования причинной связи, чем метод сходства. Благодаря эксперименту, этот метод имеет большое распространение и применение. Он служит, как мы видели, не только для определения причины, но и для определения действия.

Вторым важным преимуществом метода различия является большая, чем при методе сходства возможность получения достоверных выводов. Если в методе сходства мы всегда связаны с предположением о единственности причины, то в методе различия достоверность вывода зависит только от точности анализа сравниваемых случаев наступления исследуемого явления. Для того, чтобы обеспечить достоверность вывода по методу различия, нам необходимо лишь точно установить обстоятельства, при которых происходит исследуемое явление, а также достоверно убедиться в том, что сравниваемые нами случаи этого явления различаются только в одном обстоятельстве или в определенной совокупности обстоятельств. Но в эксперименте, с которым связано обычно применение метода различия, это сделать во многих случаях вполне возможно. Таким образом, метод различия очень часто обеспечивает достоверные выводы, поэтому он нередко применяется для проверки и доказательства предположений и догадок, полученных с помощью метода сходства в процессе наблюдения.

 

МЕТОД СОПУТСТВУЮЩИХ ИЗМЕНЕНИЙ

Этот метод, как и метод различия, может использоваться как средство для выяснения действительного статуса некоторого из предшествующих обстоятельств базисного случая. Однако, в отличие от метода различия, проверяемое здесь обстоятельство В_i не устраняется при переходе ко второму случаю, а модифицируется (изменяется) каким-то образом до В_i' если при этом некоторым образом изменяется также исследуемое явление а до а', то это является основанием заключить, что обстоятельство B_i находится в какой-то причинной зависимости с явлением а, но это не означает, что оно – обязательно причина или необходимое условие. Возможно, что это какое-то релевантное сопутствующее обстоятельство.

Итак, в качестве эмпирических данных для заключения по этому методу мы должны иметь, по крайней мере, два случая:

В₁, ..., В_i, ..., B_n – a.

В₁, ..., В'_i, ..., B_n – a'.

Эти данные являются основанием для заключения, что обстоятельство В_i является либо причиной, либо необходимым условием действия причины, либо релевантно сопутствующим обстоятельством явления а.

Например, пусть а, как и в примере на применение метода различия,– нормальная зеленая окраска растения, выросшего при обстоятельствах В₁, В₂, В₃, В₄, В₅ (см. упомянутый пример). Но если при применении метода различия переход к другому случаю состоял в устранении обстоятельства В₁ (нормального освещения), то теперь мы изменяем его интенсивность (В_i'). При этом замечаем, что изменяется и интенсивность зеленой окраски растения (а'). Отсюда заключаем, что наличие освещения является либо причиной, либо необходимым условием, либо релевантно сопутствующим обстоятельством образования хлорофилла в растениях.

Ясно, что заключение здесь более слабое, чем то, что получается по методу различия, поскольку дизъюнктивное высказывание, представляющее это заключение, включает еще дополнительную возможность, а именно возможность, что это обстоятельство является релевантно сопутствующим. В химических реакциях этим обстоятельством может служить, например, катализатор: с его количественными изменениями могут быть связаны изменения исследуемого явления а (результата реакции).

Специальное правило вывода по этому методу:

• Если два или более случаев наступления некоторого явления сходны во всех предшествующих обстоятельствах, кроме одного, которое изменяется каким-то образом от случая к случаю и при этом изменяется и исследуемое явление, то это обстоятельство находится в причинной связи с исследуемым явлением, то есть является либо его причиной, либо необходимым условием действия причины, либо релевантно сопутствующим обстоятельством.

Легко можно заметить, что метод различия является как бы частным (предельным) случаем метода сопутствующих изменений.

Если мы будем изменять какое-либо из обстоятельств в ряду обстоятельств, предшествующих изучаемому явлению, до полного исчезновения этого обстоятельства, то в пределе получим тот случай, который необходим для умозаключения по методу различия.

Существенно и то, что по этому методу мы выявляем не только причины и необходимые условия, но и релевантно сопутствующие обстоятельства.

СОЕДИНЕННЫЙ МЕТОД СХОДСТВА И РАЗЛИЧИЯ

Прежде всего надо заметить, что характеристику этого метода, как соединенного, не следует понимать так, что он в действительности представляет собой сочетание или последовательное применение двух упомянутых в его названии методов. Дело в том, что последовательное применение методов сходства и различия увеличивало бы степень правдоподобия получаемого заключения по сравнению с отдельными их применениями. Между тем метод, который здесь имеется в виду, дает, наоборот, менее правдоподобное заключение, чем каждый из указанных методов.

Если предполагать последовательное применение методов, то можно было бы иметь сочетание любых из указанных методов. Как мы уже замечали, особенно напрашивается последовательное применение метода сопутствующих изменений и метода различия, как предельного случая первого.

Соединенный же метод сходства и различия применяется в тех случаях, когда мы не можем точно учесть состав и характер предшествующих обстоятельств исследуемого явления, как это требуют методы сходства и различия.

Положим, что мы имеем ряд случаев, где есть явление а, причину которого отыскиваем, и замечаем, что среди обстоятельств, при которых происходит это явление, есть везде некоторое обстоятельство А. Если при этом в силу неясности характера и состава всех других обстоятельств, мы не имеем уверенности в том, что все случаи сходны только в этом обстоятельстве, то не можем прибегнуть к методу сходства. Тогда мы можем попытаться найти ряд случаев, где имеются обстоятельства, примерно сходные со случаями первого ряда, но явление а отсутствует. Если вместе с тем окажется, что во всех этих случаях, отсутствует также обстоятельство А, то это дает нам право с большей или меньшей степенью вероятности утверждать, что обстоятельство А находится в причинной связи с явлением а.

Таким образом, для умозаключения по этому методу надо иметь, по крайней мере, три случая вида:

 

 

Первый и второй случаи дают основание для заключения о том, что А является причиной или необходимым условием а по методу сходства, однако, без учета возможности множественности причин. Конечно, с учетом того, что имеется некоторая неопределенность, является ли сходство – в наличие обстоятельства А – среди предшествующих обстоятельств единственным (на что указывает заключение всех обстоятельств, кроме А, в скобки).

Случаи 1, 3 (или 2, 4) позволяют по методу различия также утверждать с некоторой вероятностью, что А является причиной или необходимым условием а, опять-таки с учетом упомянутой неопределенности относительно предшествующих обстоятельств.

Видно, что, при наличии посылок 3 и 4 одновременно, данный метод можно охарактеризовать как метод двойного сходства: сходство в посылках 1 и 2 в наличии обстоятельства А и явления а; в посылках же 3 и 4 – сходство в отсутствии А и а.

Подчеркнем еще раз, что заключение обстоятельств B₁, ..., В_n, как и С₁, ..., С_n, в скобки указывает, что у нас нет точной уверенности в том, что обстоятельства первого ряда сходны только в наличии А, а относительно случаев другого ряда не уверены, что наблюдаемые обстоятельства различны только в отсутствии А.

По существу, здесь речь идет уже не о методе исследования в строгом смысле этого слова, а об указании того, какие наблюдаемые данные могут служить основанием для выдвижения определенных гипотез.

Примером умозаключения о причине явления по соединенному методу сходства и различия может служить следующий. На основании данных сельскохозяйственной практики и опытной агрономии давно было известно, что растения из группы бобовых – горох, бобы, чечевица, соя, вика, клевер, люцерна и др.– не только не нуждаются во внесении в почву азотистых удобрений, но даже сами обогащают ее азотом. Благодаря этому свойству, бобовые способствуют повышению урожайности других сельскохозяйственных культур, которые сеются на полях после бобовых культур.

Причина столь интересного и важного в хозяйственном отношении явления длительное время оставалась неизвестной. Она заключалась в какой-то особенности строения бобовых растений, которую нужно было определить. И действительно, сравнение различных видов бобовых, несмотря на их разнообразие, показало, что все они имеют на корнях ярко выраженные вздутия, называемые клубеньками. В то же время у небобовых растений такие клубеньки отсутствуют. Очевидно, что здесь невозможно установить, только ли в этом обстоятельстве сходны все бобовые и отличны все небобовые растения. Однако эти наблюдения дали возможность с большей степенью вероятности заключить о том, что именно наличие клубеньков заключает в себе причину или, по крайней мере, необходимое условие их способности обогащать почву азотом.

Изучение клубеньков показало, что они вызываются особыми почвенными бактериями, которые получили название клубеньковых. Проникая в корневую систему бобовых растений, эти бактерии помогают им усваивать свободный азот, обогащая тем самым почву азотистыми соединениями.

 

МЕТОД ОСТАТКОВ

Этот метод, как его трактует Дж.Ст. Милль, сводится к следующему правилу вывода:

Если имеется сложное исследуемое явление abed, возникшее при обстоятельствах ABCD (по предположению, очевидно, причинно связанных с указанным явлением; по Миллю – возможные причины его составляющих), и если при этом известно – из предыдущих исследований,– что причина части исследуемого явления abc заключена в совокупности обстоятельств ABC, то следует заключить, что причиной d является оставшееся обстоятельство D.

Или – буквально по Миллю:

«Если из явления вычесть ту его часть, которая, как известно из прежних индукций, есть следствие некоторых определенных предыдущих, то остаток данного явления должен быть следствием остальных предыдущих (Дж.Ст. Милль. Система логики силлогистической и индуктивной.– М., 1914.– С. 361.)».

Здесь, очевидно, требуется уточнение: указанное заключение может быть правомерно выведено лишь при наличии дополнительного знания о том, что ABC не является причиной также и d. К тому же следует обратить внимание на то, что вывод такого рода не связан непосредственно с опытным исследованием. В лучшем случае в нем используются посылки предшествующих опытных исследований. По существу, это просто форма теоретического рассуждения по принципу:

Если причина какого-то явления не находится среди некоторой совокупности предшествующих обстоятельств, то она должна находиться среди других предшествующих обстоятельств, или, возможно, среди обстоятельств, которые оказались в данном случае даже неучтенными.

Не случайно, что, как правило, примеры, которые приводят авторы курсов логики, сводятся именно к тому, что заключают о наличии каких-то невыявленных обстоятельств, являющихся причинами исследуемого явления, на том основании, что причина не находится среди выявленных предшествующих обстоятельств.

Пример вывода по этому методу, ставший уже классическим,– это открытие планеты Нептун. Г.И. Челпанов (См. также: Горский Д.П. Логика.– М., 1963.– С. 262.), например, формулирует его так:

«Оказалось, что наблюдаемые движения Урана не находились в согласии с движениями, найденными посредством вычисления. Движение Урана то замедлялось, то ускорялось. Надо было определить причину нарушения движения Урана. Было известно, какое количество нарушения в движении Урана было обязано влиянию известных в то время небесных светил. Когда произвели вычитание этого известного уже воздействия, то в остатке получалось нарушение, причину которого нужно было найти. Нужно было предположить существование еще какой-то неизвестной планеты, принимающей участие в определении пути Урана. Такой планетой оказался Нептун (Челепанов Г.И Учебник логики.– М., 1946.– С. 106.)».

Как видим, действие Нептуна на Уран здесь фигурирует среди предшествующих обстоятельств. И поэтому нет и «вычитания» из совокупности предшествующих обстоятельств какой-то их части. Более того, не ясно, в чем состоит само сложное явление abed? И уж совсем этот метод не выглядит как метод эмпирического исследования, когда некоторые авторы трактуют упомянутое Миллем «вычитание» (каких-то обстоятельств из некоторой совокупности) как простое арифметическое действие. Как мы видели, близок к этому и Г.И. Челпанов.

В заключение еще раз обратимся к вопросу о связи изложенных методов с индуктивными умозаключениями. Мы уже упоминали, что основные идеи, лежащие в основе метода сходства, различия и соединенного метода сходства и различия, используются в выводах неполной индукции при специальном отборе данных, выраженных в посылках. Кроме этого было отмечено, что эти методы могут служить средством обоснования индуктивных обобщений. Например, по методу неполной индукции мы можем заключить, что «все медведи, обитающие на Северном полюсе, имеют белую окраску». Обоснованием этого обобщения могло бы служить установление причины указанной особенности белых медведей. Непосредственно наблюдаемая причина состоит, очевидно, в цветовой характеристике самой среды обитания этих животных.

Индуктивное обобщение относительно того, что все кристаллические вещества имеют определенную температуру плавления, может получить дополнительное обоснование, если установить, в частности, используя данные методы, что именно кристалличность является причиной указанной их особенности.

Наконец, полезно обратить внимание и на то, что данные методы могут применяться не только для установления причинных связей, но и для выяснения вообще необходимых связей между признаками тех или иных явлений. По крайней мере, они могут играть некоторую эвристическую роль в возникновении гипотез относительно таких связей. Мы можем, например, заметить, что всегда, когда число делится на 3, то сумма цифр его тоже делится на 3. Когда же последний признак отсутствует, то отсутствует и делимость числа на 3. На основе этих наблюдений, соответственно по методу сходства и различия,– хотя и при нестрогом их применении – мы можем прийти к гипотезе о необходимой связи указанных признаков.

Однако подчеркнем еще раз ограниченность этих методов, как способов научного познания: она состоит в том, что с их помощью мы можем выяснить такие причины явлений, которые относятся к числу наблюдаемых обстоятельств. Кроме того, как мы видели, при их применении обычно не обусловлена достоверность заключений.

К тому же, устанавливая с помощью этих методов причинную связь тех или иных явлений, мы не имеем ответа на вопрос, какова природа этой связи, в чем именно она состоит? Каким образом, например, кристалличность тех или иных веществ обусловливает (детерминирует) наличие у них определенной температуры плавления? Ответы на вопросы этого рода дает научное объяснение явлений и их связей (см. § 43).

 

Упражнения

 

1. При расследовании одного уголовного дела было установлено, что на пункте общественного питания отравилось пять человек. Было выявлено, что один из пострадавших ел осетрину, щи, шницель, кофе; другой – икру, борщ, шницель, сметану; третий – семгу, икру, говядину по-монастырски, шницель, мороженое; четвертый – щи, студень, шницель, кисель; пятый – салат из капусты, кильку, бульон, шницель, компот и много хлеба.

На вопрос, каков источник отравления, следователь ответил, что пока (до вскрытия) ничего определенного сказать нельзя. Согласны ли Вы с его мнением? Обоснуйте свой ответ.

2. При расследовании другого дела было установлено, что пострадавший ел селедку, борщ, котлеты, компот. Следственными мероприятиями был обнаружен человек, который ел сметану, суп, жареную рыбу и компот в этой же столовой без признаков отравления.

На вопрос об источнике отравления следователь дал ответ как и в предыдущем случае. Согласны ли Вы с его мнением? Аргументируйте свой ответ.

3. Известно, что явлению а предшествуют обстоятельства А, В, С. Какие опыты нужно проделать и какие данные получить для установления причинной связи между Си а по методу различия, сходства и сопутствующих изменений?

4. По какому методу установления причинных зависимостей сделаны следующие заключения и состоятельны ли они?

а) Без примеси углерода железо легко куется. При добавлении небольшого количества углерода железо куется труднее. При большом количестве добавленного углерода железо вообще не куется. Отсюда делается заключение, что присутствие углерода является причиной ухудшения ковкости железа.

б) Освященная священником вода долго не портится, в то время, как обычная вода, повседневно используемая в хозяйстве, портится быстро. Значит, освящение воды священником предохраняет воду от порчи.

в) Одну мышь поместили в атмосферу, лишенную кислорода. Другая находилась в обычных условиях. Первая мышь погибла. Так, мы заключаем, что кислород необходим для жизни.

г) Некий школьник утверждал, что органы слуха у пауков находятся на ногах...

Положив пойманного паука на стол, он крикнул: «Бегом!» Паук побежал... Затем он оторвал пауку ноги и, снова положив его на стол, скомандовал: «Бегом!» Но на сей раз паук остался неподвижен. «Вот видите,– торжествующе заявил юный экспериментатор,– стоило пауку оторвать ноги, как он сразу оглох».

ТЕОРИЯ И НЕКОТОРЫЕ МЕТОДЫ ТЕОРЕТИЧЕСКОГО ПОЗНАНИЯ

§ 42. Теория как форма и система знания

Теория – наряду с понятиями и суждениями – представляет собой одну из форм отражения (воспроизведения) действительности в мышлении. Однако, в отличие от понятия и суждения, теория не является, вообще говоря, отдельной мыслью – если не иметь в виду вырожденные случаи теории, в качестве каковых рассматривают иногда отдельные суждения, выражающие, например, законы науки.

Теория представляет собой некоторую систему знания, относящуюся к некоторой области действительности или к некоторым аспектам той или иной области действительности. Предметом астрономии, например, является, очевидно, особая область реальной действительности – небесные тела, тогда как география и геология изучают определенные аспекты такой области реальной действительности, как планета Земля. Логика, психология, физиология высшей нервной деятельности изучают разные аспекты мышления человека; социология, экономическая теория, история – различные аспекты общественной жизни.

Предметом теории могут быть и особые классы явлений: теория теплоты, электричества, магнетизма и т.д., а также некоторые аспекты действительности вообще: теория пространства и времени, философия. К особому классу теорий относятся теории методологического характера, изучающие методы и приемы познания. К их числу относятся, например, многие разделы математики (теория математического анализа, вариационного исчисления, теория дифференциальных уравнений) и значительная часть содержания логики.

Как система знания – в отличие от простой совокупности знаний, каковой является, например, обыденное знание – теория включает в себя определенный круг понятий и высказываний, логически связанных между собой так, что одни понятия, или термины вообще, определяются через другие. Одни суждения связаны по смыслу с другими, определенным образом субординированы или даже выводятся из других.

Весьма существенными характеристиками теорий являются также указания на основные задачи, функции теории. Таковыми являются систематизация и объяснение изучаемых явлений, а также выявление законов изучаемой области или аспекта действительности. Наиболее важной функцией теории является объяснение. Часто, например, даже говорят, что объяснить явления некоторого класса – это значит построить теорию этих явлений; можно сказать и наоборот: построить теорию – значит объяснить какие-то явления. Важность функции объяснения очевидна в естественно-научных теориях. В физике мы объясняем суть тепловых, световых, электрических явлений, явлений магнетизма и звука и т.д. В химии – суть химических реакций или имеющихся результатов химических процессов. Законы движения в механике также объясняют нам, каким образом взаимосвязаны такие факторы, как сила, масса, ускорение, путь и скорость движения и т.п.

Правда, при более широком употреблении термина «теория» в практике научного познания выделяются и такие теории, которые ограничиваются лишь описанием и систематизацией некоторого эмпирического материала и возможно содержат те или иные индуктивные обобщения,– эмпирические теории (минералогия, ботаника, география, анатомия). Иногда такие теории называют феноменологическими.

Заметим, что в математической и логической литературе теорию принято определять как множество (совокупность) высказываний, замкнутое относительно логической выводимости. Это значит, что в ту или иную теорию включаются не только уже известные высказывания, но и те, которые могут быть выведены из известных. Конечно, это определение выделяет важную характеристику теории и в некоторых исследованиях теорий логического и математического характера является вполне достаточным. Но оно не отражает другие, существенные с гносеологической точки зрения характеристики этой формы знания. И в особенности именно то, что теория представляет собой некоторую систему знания. И при этом знания, в большей или меньшей степени обоснованного.

 СОСТАВ ТЕОРИЙ

В составе теории, особенно естественно-научной, хотя и не только таковой, выделяют обычно эмпирический базис – совокупность фактов, устанавливаемых посредством наблюдений. Например, к эмпирическому базису молекулярно-кинетической теории строения вещества относятся знания о наличии в действительности явлений диффузии жидкостей и газов, а также (в определенной мере) и твердых тел; испарение жидкостей; различие и изменения агрегатных состояний тел; броуновское движение и т.п.

Научные данные, относящиеся к эмпирическому базису, составляют исходный материал для теоретических построений. Поэтому, употребляя термин «теория» в более строгом смысле, его отделяют от собственно теории, не включая в состав последней.

Как уже было сказано, теория есть совокупность взаимосвязанных понятий и высказываний. Среди понятий теории различаются два основных типа:

1. В понятиях первого типа выделяются и обобщаются основные характеристики и компоненты изучаемых явлений. Например, в механике выделяются такие характеристики механического движения предметно-функционального типа, как траектория, скорость, ускорение, а также сила, масса, импульс, кинетическая энергия и т.п.

2. Другую группу понятий – понятий классификационного характера – составляют понятия, в которых выделяются классы изучаемых предметов и явлений (объектов вообще). Посредством этих понятии осуществляется классификация этих явлений. Причем, основаниями этих классификаций являются обычно упомянутые выше характеристики. Например, в механике, наряду с основным понятием «механическое движение» выделяются такие его виды, как «прямолинейное», «криволинейное», «колебательное», а также «равномерное», «неравномерное», «равноускоренное» и «неравноускоренное» и т.д.

На два этих типа делятся как эмпирические, относящиеся к эмпирическому базису, так и, соответственно, теоретические понятия теории. На теоретическом уровне познания мы, в частности, детализируем, углубляем эмпирические понятия. В той же механике на этом уровне при использовании методов математического анализа появляются такие понятия, как «равнозамедленное» и «равноускоренное движение», «импульс», «кинетическая энергия», «мгновенная скорость» и «мгновенное ускорение» и т.д.

Основную роль в теориях играют высказывания. Они так же, как и понятия, могут относиться к эмпирическому базису и к собственно теоретическому уровню теории. Среди последних особо выделяются два вида:

1. Высказывания, в которых выражается знание законов изучаемой действительности и которые называются законами данной теории или науки (законы физики, химии, математики и т.д.).

2. Так называемые предложения соответствия (точнее, интерпретационные высказывания).– Их характеризуют обычно как предложения, выражающие связи между терминами, обозначающими нечто наблюдаемое, и теоретическими терминами. Например: «Теплота тела (наблюдаемое) – это кинетическая энергия хаотического движения частиц, составляющих это тело (теоретическое)», «Температура тела – показатель средней скорости движения его молекул», «Электрический ток – это поток электрически заряженных частиц».

Точнее, как можно видеть из примеров, предложения соответствия – это утверждения, раскрывающие сущность наблюдаемых явлений. С логической точки зрения это реальные определения соответствующих явлений (§ 24). В них содержится объяснение наблюдаемых явлений.

Высказывания того и другого вида представляют собой утверждения необходимого характера (см. § 33), в отличие от утверждений фактического характера, каковыми являются утверждения, относящиеся к эмпирическому базису теории.

ИСТИННОСТЬ ТЕОРИЙ

Важной характеристикой теории является степень ее обоснованности, ее практическая подтверждаемость. Каждый ученый, который действительно стремится иметь знания о явлениях изучаемой им области (а не просто произвольные построения, хотя бы и позволяющие решать некоторые задачи и удовлетворяющие определенным эстетическим требованиям (Есть такие философы-методологи науки, которые видят задачу научного познания именно в изобретении теоретических концепций, удовлетворяющих указанным требованиям способности служить решению некоторых задач, простоты, изящества и т.п.)), всегда стремится иметь истинные теории, то есть такие теории, утверждения которых соответствуют изучаемой действительности. Хотя случается и так, что теории оказываются и ложными. Таковыми, например, являются известные в истории теории флогистона, теплорода, неправильно объясняющие явления горения и тепловые процессы.

Основным и наиболее общим критерием истинности теорий, как и высказываний вообще, является общественная практика, включающая производственную деятельность, эксперименты и вообще применение теоретических знаний в той или иной деятельности людей. При этом деятельность не обязательно должна быть материальной. Так, конкретная научная деятельность, в которой применяются результаты математики и логики, является сферой их практического применения, а тем самым и сферой проверки этих знаний.

Вместе с тем практика не является абсолютным критерием истинности наших знаний. Это верно в трех отношениях. Во-первых, он не всегда применим – по крайней мере, непосредственно – для проверки высказываний. Например, для проверки высказываний о необходимости каких-то явлений, о будущих событиях. Во-вторых, практика может подтверждать и некоторые ложные высказывания (до некоторых пор в опыте подтверждались утверждения указанных ложных теорий теплорода, флогистона). И наконец, как уже было сказано, практика лишь подтверждает, но не доказывает истинность утверждений теории. В лучшем случае они обеспечивает практическую, но не логическую достоверность, то есть близкую к единице, но не равную единице, вероятность их истинности.

Необходимым условием и тем самым важным логическим критерием истинности теорий является их логическая непротиворечивость, то есть взаимная согласованность утверждений теории между собой, последовательность в объяснении явлений.

Однако и истинные теории, как правило, не представляют собой абсолютно точного знания своего предмета. Сказанное прежде всего относится к теориям естественно-научного характера, предметом которых являются некоторые области или аспекты реальной действительности. Это означает, что теория не представляет собой законченного образования. В истории познания наблюдается постоянная смена теорий, связанная с углублением нашего знания: Эвклидова геометрия получила дальнейшее развитие в неэвклидовых, классическая механика (Галилея, Ньютона) – в релятивистской и квантовой теориях.

ВИДЫ ТЕОРИЙ

Теории различаются прежде всего по своему предмету, по характеру изучаемой или области или аспекта действительности, а тем самым и по характеру рассматриваемых объектов.

Среди существующих теорий большой класс составляют теории, изучающие те или иные области или аспекты реальной действительности (конкретные науки). К другому классу относятся теории, имеющие дело с идеальными областями или вообще с явлениями ненаблюдаемого характера (абстрактные науки).

Среди первых особо выделяются естественно-научные (физика, биология, теории, составляющие медицину, химия и т.п.) и гуманитарные теории (философия, социология, этика, эстетика – науки в более широком смысле). Грань между ними провести вообще довольно трудно. Вторые связаны с человеком и с различными аспектами его жизнедеятельности, хотя и среди естественно-научных есть такие, которые также изучают человека: его анатомию, физиологию и т.д. По-видимому, деление идет здесь по степени наблюдаемости изучаемых явлений. В первом случае – это непосредственно наблюдаемые явления. Во втором – это явления, наблюдаемые некоторым опосредованным образом, через те или иные проявления их в жизни. В последнем случае речь идет собственно о явлениях, связанных с человеком, о таких его проявляемых в жизни характеристиках, как психика, эстетические или этические взгляды и убеждения, характеристики употребляемого им языка, явления и объекты культуры, миропонимание и т.п.

Среди наук, изучающих области идеальной действительности, следует прежде всего выделить математику и логику, вернее, теории, относящиеся к математике и логике. Это теории, изучающие абстрактные и идеальные объекты и методы научного познания.

Другим основанием деления теорий на виды является способ их построения.

Наиболее четко выделяются по своему строению аксиоматические теории. Само их название говорит о том, что в них выделяется особая часть – системы аксиом. Это совокупность высказываний, которые принимаются за истинные (постулируются как истинные). Наряду с аксиомами в них первоначально выделяются некоторые понятия, необходимые для точной формулировки аксиом.

Аксиомы иногда определяют как очевидно истинные утверждения, не требующие доказательств. Однако в науке дело обстоит не так. Аксиомы бывают далеко не очевидными и более того, они сами в большей или меньшей степени обосновываются, но не внутри самой теории. Например, аксиомы геометрии принимаются в результате некоторого их обоснования в практической деятельности, в которой мы имеем дело с теми или иными фигурами и телами. Кстати, к вопросу об обосновании аксиом заметим, что аксиомы логических исчислений, как правило, строгим образом обосновываются в семантике соответствующих дедуктивных теорий. Важную часть аксиоматической теории составляет совокупность утверждений, логически выводимых из аксиом – производные утверждения теории.

Примерами таких теорий являются рассмотренные выше аксиоматически построенные логические исчисления (см. § 10, 11), аксиоматическая теория множеств и аксиоматическая арифметика в математике. В настоящее время аксиоматизирована геометрия, аксиоматизированы некоторые физические теории, например, механика.

Однако большинство теорий не являются аксиоматизированными, хотя в них тоже есть некоторые исходные утверждения, но нет четкого разделения на исходные и производные – выводимые из них. Причем даже те, которые более или менее выделяются как исходные, имеют определенное обоснование в самой теории. Эти теории называют гипотетико-дедуктивными. Хотя следует уточнить, что эта характеристика указывают не на особенность их строения, а на способ, методы их формирования и развития: таковым является гипотетико-дедуктивный метод познания. Он состоит в том, что, исходя из какого-то множества наблюдаемых явлений, мы строим вначале некоторые гипотезы, объясняющие эти явления. В ряде случаев, когда речь идет об установлении законов между явлениями, эти гипотезы получаются посредством индуктивных обобщений. Объяснительные гипотезы обычно являются результатами мыслительной творческой деятельности человека, которая не сводится к каким-либо известным логическим приемам, не регламентируется теми или иными правилами: основную роль в них играет интуиция, изобретательность. Далее идет проверка, обоснование выдвинутых гипотез. Как говорилось уже ранее (§ 39), основную роль в этом процессе обоснования гипотез играют дедуктивные «извлечения» из них следствий, которые проверяемы путем наблюдения, и собственно проверка этих следований. Особую надежность теории придает реализация каких-то ее следствий в практической деятельности и оправдание при этом ожидаемых результатов.

Такой процесс дедукции и проверки ее результатов расширяет круг известных нам явлений. При этом зачастую открываются явления, не объясняемые данными гипотезами и даже противоречащие им. В таких случаях происходит корректировка гипотез, их уточнение, обобщение и т.д., а иногда, конечно, и просто отбрасывание их как ложных. Таким образом, гипотетико-дедуктивный метод – это форма постоянного взаимодействия теоретического и эмпирического исследования.

 

 Научное объяснение

Заметим прежде всего, что в литературе по логике научного познания существует так называемая логическая модель научного объяснения (теория Гемпеля-Оппенгейма).

Согласно этому представлению, научное объяснение какого-то явления Н (зафиксированного в истинном единичном высказывании «Н») представляет собой логический вывод, посылками которого являются некоторая непустая конечная совокупность законов L₁, ..., L_n той области действительности, к которой относится объясняемое явление Н, и некоторое такое истинное единичное высказывание Е (выражающее, например, условие, при котором происходит Н), которое указывает на определенное явление (факт, признак) из той же области; заключением же вывода является Н. При этом объяснение может быть дедуктивным и вероятностным в зависимости от того, каков характер логического следования, лежащего в основе этого вывода.

Не вдаваясь в подробности, скажем, что это понимание объяснения не выражает, по-видимому, сути того, что в науке обычно имеют в виду под этим термином: «объяснение», построенное по этой схеме может вообще не содержать никакого объяснения интересующего нас явления! Действительно, может ли, например, удовлетворить кого-либо объяснение, почему медь электропроводна, построенное – в соответствии с указанной моделью – в форме следующего вывода:

 

 

Ясно, что здесь снова напрашивается вопрос: а почему металлы электропроводны? Без этого неясен и ответ на поставленный вопрос о меди...

Здесь мы подошли, во-первых, к различению объяснения явлений и объяснения законов науки.

Объяснение явления. Объяснение явления должно отвечать на вопросы: что оно представляет собой, почему и как происходит? При объяснении тех или иных природных явлений того или иного вида должна быть указана их сущность (см. § 14). Например, электропроводность вещества состоит в том, что при помещении его в электрическое поле (при возникновении разности потенциалов) в нем возникает электрический ток, то есть поток электрически заряженных частиц. Углубляя объяснение, ссылаются также и на причину возникновения этого потока, каковой является, в конечном счете, взаимное притяжение частиц с противоположными зарядами и отталкивание одноименно заряженных частиц (Последнее указывает уже на существование определенного закона, который сам может потребовать объяснения того, почему именно противоположные частицы притягиваются друг к другу, а одинаковые – отталкиваются друг от друга (см. ниже).). Молния представляет собой мгновенный электрический разряд между облаками или облаком и Землей (возникающий опять-таки в силу разности потенциалов). Испарение жидкости есть результат отрыва поверхностных молекул жидкости от данной массы жидкости. Причина этого явления состоит в том, что кинетическая энергия движения отрывающихся молекул позволяет им преодолеть взаимное притяжение молекул в массе жидкости.

Так или иначе – явно или неявно – в объяснениях этого вида имеется указание на причину, вызывающую данное явление (см. § 40). Поэтому обычно их называют каузальными и говорят даже, что объяснить какое-то явление – это значит, указать его причину.

Однако наиболее важной частью объяснения явления выступает не указание причины самой по себе, а раскрытие механизма ее действия. Более того, возможны объяснения, не содержащие даже прямого указания на причину, но раскрывающие механизм ее действия, что, собственно, и составляет сущность некоторого явления. Объясняя, например, что такое молния, мы можем в каких-то случаях ограничиться указанием на то, что это мгновенный электрический разряд, мгновенное перетекание электрически заряженных частиц с одного облака на другое или с облака на Землю. К тому же причиной, например, наличия у предметов того или иного вида каких-то специфических свойств является сама их сущность. Мы видели выше (см. § 14), что выявление сущности предметов некоторого вида позволяет объяснить, почему именно им необходимо обладать некоторыми общими свойствами, то есть объяснить причину их качественной специфики.

Некоторую особенность имеют объяснения явлений общественной жизни, поступков, поведения людей. Здесь главную роль играет выяснение мотивов, целей поведения людей (или определенных групп людей) в их соотношении с моральными принципами и установками. Объяснения этого рода принято называть телеологическими объяснениями.

Распространенно мнение, что цель, мотив, под влиянием которого человек осуществляет какое-то действие, не является причиной этого действия. Однако такое абсолютное противопоставление цели и причины едва ли можно признать правильным. По крайней мере, цель в сочетании с волей человека, направленной на осуществление намеченного действия, является его причиной. Однако мы подчеркивали раньше, что причина вызывает действие при наличии определенных условий. И если в природе часто можно достаточно точно выявить круг таких условий, то в обществе это возможно, по-видимому, лишь в очень простых случаях. Но если действительно какая-то цель осуществляется, то это указывает, конечно, на то, что была соответствующая совокупность условий и цель – в сочетании с волей – проявила себя именно как причина.

Учитывая введенное ранее различение ближайшей причины некоторого явления и более отдаленной (см. § 40), в каких-то случаях при объяснении общественных явлений полезно и даже необходимо – особенно при объяснении массовых общественных явлений – ставить вопрос и об объяснении причины появления самих целей и воли людей к их осуществлению. Это вопрос уже не о непосредственных, а о более глубоких причинах явления и, соответственно, о более глубоком их объяснении.

Объяснение законов науки. Строго говоря, имеется в виду объяснение повторяемости явлений, фиксируемая в формулировках законов науки.

Исходным при таком объяснении обычно является некоторое индуктивное обобщение. Результат такого обобщения – вида «Все S суть Р» – указывает на наличие повторяемости: везде, где есть S имеется Р. Результат объяснения этой повторяемости может быть двояким:

1) устанавливается, что указанная повторяемость является случайной. Так, считается, что случайным является наличие у всех людей мягкой мочки уха, парнокопытность всех жвачных животных;

2) выясняется, что повторяемость имеет место в силу наличия некоторой связи между S и Р.

В последнем случае – если эта связь установлена – индуктивное обобщение приобретает статус закона науки. Таким образом, сам закон науки становится результатом объяснения.

Поскольку связь между явлениями или признаками S и Р означает детерминированность (обусловленность) одного другим, постольку объяснение состоит в том, чтобы показать, почему всегда (обязательно, а не случайно – иначе нет закона) Р сопровождает S. Иначе говоря, должен быть показан механизм взаимосвязи («сцепления») S и Р (механизм перехода от одного к другому). Для этого необходимо выяснение сущности как S, так и Р, ибо связь, которую выражает закон, выявляется именно на уровне сущности соответствующих признаков или явлений.

Возвращаясь к примеру объяснения того, почему медь электропроводна, мы должны были бы указать, что ее атомы – как и атомы всех металлов – обладают низким коэффициентом ионизации, то есть легко «теряют» свои внешние электроны. В силу этого в массе медного тела или проводника имеются свободные электроны, которые при возникновении разности потенциалов на концах проводника начинают «перемещаться», то есть образуют электрический ток. Поскольку медь здесь выступает просто как представитель класса металлов, данное объяснение можно рассматривать как объяснение повторяемости металл (S) – проводник (Р), результатом которого является закон: «Все металлы – проводники». Таким образом, медь проводник не потому, что все металлы проводники, как это получается согласно модели Гемпеля, а наоборот, все металлы проводники, потому что они имеют общую с медью сущность, то есть будучи простыми веществами, состоят из атомов с низким коэффициентом ионизации.

Данный пример указывает на возможность установления закона, относящегося к классу некоторых явлений, на основе объяснения отдельных явлений этого класса.

Так, Карно установил общий закон работы паровых машин («цикл Карно») на основе анализа сущности происходящих в них процессов, отнюдь не обращаясь к множеству паровых машин.

Вспомним также доказательства геометрических теорем в школьном обучении. Для доказательства, например, того, что всякий треугольник имеет сумму внутренних углов, равную 180° (закон эвклидовой геометрии) рассматривают некий отдельный треугольник. Переход от отдельного к общему оправдан при этом тем, что при рассмотрении взятого треугольника учитывают только те его свойства, которые, по определению, являются общими для всех треугольников (замкнутость, ограниченность тремя прямыми).

Вывести какие-то свойства предмета из его сущности – значит установить необходимость присущности ему этих свойств. А согласно эпистемическому принципу «необходимость есть всеобщность», это означает также установление общего утверждения о принадлежности данных свойств всем предметам, обладающим данной сущностью (всему классу предметов, обладающих данной сущностью).

Возвращаясь к вопросу об обосновании индуктивных обобщений, заметим, что в случае выяснения причин повторяемости S и Р посредством применения какого-либо из методов установления причинной зависимости явлений (см. § 41), мы получаем уже некоторое обоснование индуктивного обобщения, и, можно сказать, некоторое частичное объяснение этой повторяемости. Мы видели, что таким именно образом может быть обосновано и частично объяснено обобщение «Все кристаллические вещества имеют определенную температуру плавления», если установлено, что причиной указанной особенности кристаллических веществ является именно их кристаллическое строение. Однако для объяснения этого обобщения в строгом смысле слова надо обратиться к сущности теплоты, к сущности самого процесса нагревания и повышения температуры тела. Нагревание – сообщение телу теплоты – это увеличение кинетической энергии составляющих его молекул. У кристаллического вещества превращаемая кинетическая энергия затрачивается до некоторых пор на разрушение кристаллической структуры. И только после полного разрушения кристаллов – то есть после превращения твердого вещества в жидкость – оно (продолжающееся нагревание) приводит к увеличению средней скорости движения молекул, что и означает повышение температуры. Точка плавления кристаллического тела – это и есть та температура, которая сохраняется в течение разрушения его кристаллической структуры.

В заключение данного раздела обратим внимание на то, что объяснение связано с определенными типами вопросов (см. § 44):

– «Что?» (что представляет собой явление или предметы некоторого класса?);

– «Почему?» (какова причина тех или иных явлений или каких-то особенностей у предметов некоторого класса?);

– «Каким образом?» (каков механизм действия причины, каков механизм обусловленности, взаимосвязи явлений?).

Как мы видели, при объяснении явлений и законов ответы – объяснения – на эти вопросы могут совмещаться. Если при объяснении явления указывается не просто его сущность, но и причина и механизм ее действия, то имеем ответ на вопросы всех указанных типов. При объяснении законов выясняются ответы на вопросы «почему?» и «каким образом?».

Естественно выделить и особый вид объяснения, играющий важную роль в педагогической практике. Это – объяснение, представляющее собой ответ на вопрос «каким образом?», разъясняющее процедуры решения тех или иных массовых задач (объяснение алгоритмов), например, каким образом найти наибольший общий делитель двух чисел, наименьшее кратное для них, как найти знаменатель геометрической прогрессии, сумму ее членов и т.п.

Ясно, что объяснение неразрывно связано с пониманием, именно с пониманием того, что представляют собой те или иные явления, как и почему они происходят. Правда, термин «понимание» можно употреблять и часто употребляют в некотором психологическом смысле. В этом смысле человек может не понимать самого объяснения, что в педагогической практике, кстати, нередко и случается. Непонимание этого рода опять-таки, по-видимому, связано с механизмом употребления языка. Чаще всего оно, как кажется, является следствием неумения связать употребляемые словесные знаки с теми предметами и явлениями, свойствами и отношениями, которые составляют предметное значение этих знаков, то есть следствием непонимания смысла и незнания предметных значений или неточности этих знаний.

 

 Вопрос и гипотеза как формы познания. Их методологическое значение

ВОПРОС

Как мы надеемся, читатель имеет уже определенное представление о процессе познания и некоторых методах его осуществления в науке. Результатами познания являются те или иные формы знания, и ясно, конечно, что для осуществления процесса познания существенной является задача оформления и фиксации этих результатов. Но не менее важно в этом процессе уметь фиксировать и то, что является еще неизвестным и требует выяснения. Формами, в которых мы фиксируем знание того, что мы еще не знаем, что подлежит выяснению, являются как раз вопросы. Для понимания структуры вопроса подчеркнем: выделение того, что нам неизвестно, осуществляется всегда в рамках чего-то известного, познанного. Например, нам известно, что тела состоят из молекул, и в рамках этого знания могут теперь возникать вопросы: что представляют собой сами молекулы, какова их величина, сколько молекул находится в некоторой единице объема вещества, связаны ли они между собой в телах или свободно двигаются и т.д., и т.п.

• Вопрос, как форма познания, есть способ выделения неизвестного, подлежащего познанию, в рамках чего-то известного.

Отсюда ясна и методологическая роль вопроса. Он определяет цель дальнейшего научного исследования, а тем самым и направление научного поиска. Мы говорили раньше, что мышление – это активный и целенаправленный процесс и такой характер его обусловлен именно тем, что он начинается всегда с некоторого вопроса (конечно, речь идет о познавательных процессах мышления, а не о стихийном, не о самопроизвольном брожении мыслей).

Едва ли надо говорить, какую роль играют вопросы в процессах коммуникации людей. С вопросов обычно начинается знакомство людей, посредством вопросов люди узнают друг друга и т.д.

Знаковой формой вопроса в естественном языке является вопросительное предложение. Оно, наряду с побудительным предложением, представляет собой фактически одну из семантических категорий языковых выражений, то есть является знаком определенного типа. Однако, как отмечалось (см. § 6), до сих пор в логике как и в науке о знаках вообще – семиотике – не выяснено, каково предметное значение, а также и смысл выражений этого типа.

В логике существует определение вопроса как запроса некоторой информации. Иначе говоря, вопрос трактуется как побудительное предложение: «Представьте, пожалуйста, такую-то и такую-то информацию!» Однако из указанной роли вопроса в познании ясно, что ученый прежде всего ставит вопросы перед самим собой... Но едва ли он обращается с запросом о предоставлении ему информации к самому себе... Как кажется, можно в какой-то мере трактовать только что упомянутым образом вопросы, возникающие в процессе коммуникации людей, в частности, в процессах анкетирования, экзаменов. Однако и в таких случаях в вопросе всегда выявляется то, что человек находит нужным выяснить. А экзамен к тому же – при определенной его организации – представляет собой некоторую имитацию познавательного процесса. Ясна, например, желательность того, чтобы экзаменующийся не просто помнил бы ответы на вопросы, но и представлял бы себе процедуру и аргументацию, которые приводят в науке к этим ответам. Известно, что способные люди, например в математике, стремятся не запомнить готовые результаты, а воспроизводить их, когда это нужно.

Имеются четыре основных вида вопросов, которые, как может показаться, имеют довольно странные названия:

Ли-вопросы;

Какой (кто, какие)-вопросы;

Сколько-вопросы;

Что (как, почему)-вопросы.

Ли-вопросы таковы, например: «Является ли чугун металлом?», «Все ли теплокровные позвоночные?», «Существуют ли кислоты, не содержащие кислорода?», «Многие ли водные животные являются холоднокровными?» Это вопросы, ответами которых могут служить просто «да» или «нет», или в сочетании с высказываниями, которые представляют знание того, что не было известно: «Нет, чугун не является металлом», «Да, все теплокровные животные являются позвоночными».

Однако нетрудно заметить, что такие вопросы, как «Какая кислота не содержит кислорода?», «Какие водные животные являются теплокровными?» относятся явно к другому типу. Это – как раз вопросы типа «Какой (кто, какие)?» В качестве ответов на них мы должны, очевидно, назвать неизвестный предмет, ряд предметов или видов некоторого класса: «Соляная кислота», «Киты и дельфины».

Сколько-вопросы употребляются, когда нас интересуют количественные характеристики тех или иных явлений. «Сколько имеется простых чисел между 2 и 11?», «Какова длина земного экватора?» (здесь может подразумеваться сколько километров или метров составляет эта длина?).

Что-вопросы выражают незнание того, что представляет собой некоторое явление, какова причина некоторого события или что обозначает некоторое слово (например, «Что обозначает слово «дескрипция»?). Поскольку явление обычно многосторонне, то и вопрос может разбиваться на некоторые подвопросы, выдающие аспекты явления: почему-вопрос (какова причина явления) или, когда подразумевается какая-то связь с практикой,– для чего-вопрос (какова цель действия); как-вопрос (в чем суть явления, например, молнии, закипания воды и т. п., каков механизм его возникновения). При таком разбиении вопрос становится сложным, то есть представляет собой некоторую совокупность подвопросов.

Специфика что-вопросов состоит в том, что ответами на них являются объяснения каких-то явлений. И здесь имеются две возможности: 1) когда ответом является реальное определение предмета: что представляет собой теплота, температура? Что представляет собой предикат как функция? (какова специфика его как функции?); 2) вторая возможность, когда ответ – это объясняющая теория и естественно, что такой ответ не может быть выражен в отдельном суждении и без привлечения определенных понятий. Иначе говоря, ответ на такой вопрос – это именно какая-то теория. Таковыми являются как раз теория происхождения Солнечной системы, теория строения атомного ядра и т.п.; они именно являются ответами на вопросы: как произошла Солнечная система, почему в ней имеют место те или иные особенности, например вращение всех планет вокруг Солнца, при этом в одной плоскости, вращение их вокруг своих осей? и т.д.

То известное, то есть имеющееся знание, в рамках которого выделяется подлежащее выяснению, называется предпосылкой вопроса.

Наиболее простой характер имеют предпосылки ли-вопросов. Для вопроса вида «Верно ли А?» (имеет ли место ситуация А?) предпосылкой является высказывание вида «А или неверно, что А». Например, предпосылка вопроса: «Все ли водные животные являются холоднокровными?» есть подразумеваемое высказывание «Все водные животные являются холоднокровными или не все они таковы». По-видимому, высказывания указанного вида (А или неверно, что А) представляют собой частные случаи закона исключенного третьего лишь для правильно сформулированных высказываний. А к числу неправильно сформулированных, как уже раньше подчеркивалось, относятся, в частности, высказывания субъектно-предикатного типа, в которых предикатор применяется к предметам, не относящимся к области его определения, вроде, «Все четные числа разумны», «Цицерон есть простое число» и т.п.

Для приведенных выше вопросов других типов «Какая кислота не содержит кислорода?», «Какие водные животные являются теплокровными?» предпосылками являются знания, высказывания: «Есть такие кислоты, которые не содержат кислород», «Среди водных животных имеются теплокровные». Вопрос «Будешь ли ты сегодня вечером дома?» имеет в качестве предпосылки сложное высказывание или совокупность высказываний: «У данного человека есть дом и, по крайней мере, иногда, но не всегда, он бывает по вечерам дома».

Критерий правильности постановки вопросов. Вопрос может быть поставлен правильно или неправильно прежде всего в зависимости от того, истинны или неистинны его предпосылки.

Ясно, что вопросы «Кто зажигает звезды?», «Кто изобрел иррациональные числа?» «Какие простые числа являются тяжелыми?» явно неправильны как раз в силу того, что звезды никто не зажигает, то есть неверна предпосылка, что звезды кто-то зажигает; иррациональные числа никто не изобрел (не путать изобретение с открытием!); что касается третьего вопроса, то его предпосылка «имеются тяжелые простые числа» не только не истинна, но и бессмысленна.

Правда, кажется, что некоторые вопросы не имеют предпосылок. Например: «Знаете ли Вы этого человека?» (подразумевается, что имеется указание на определенного человека). Тогда напрашивается вывод – если правильность или неправильность вопроса связывать только с истинностью или неистинностью предпосылок, как это обычно и делается,– что подобные вопросы нельзя оценивать ни как правильные, ни как неправильные. Однако только что приведенный вопрос неправилен потому, что неясно, каковым должен быть ответ на него, знать можно фамилию человека, профессию, его физические и нравственные качества и т.д. Он не имеет предпосылки как раз в силу именно того, что неясно, что подлежит выяснению согласно этому вопросу. Конечно, тот, кто ставит такой вопрос, должен был конкретизировать его, то есть уточнить, какие сведения об этом человеке его интересуют. Тот же, кому был адресован вопрос, мог формально ответить «знаю» или «не знаю», но в этих ответах, по существу, нет никаких сообщений. Однако предъявить претензии к нему по этому поводу было бы явно несправедливо: вина за это лежит на задающем вопрос. Кстати, известны недоразумения, случающиеся на экзаменах в силу как раз того, что неясный характер имеют обращенные к экзаменуемому вопросы.

Вообще, второй причиной неправильно поставленных вопросов может быть неясность в их формулировках. Неясность может быть и с грамматической (синтаксической) точки зрения, и с точки зрения смысла, и т.д. Но основное – неясен характер ожидаемого ответа.

Бывает в жизни и так, что из-за неясности поставленных вопросов лица терпят большие неприятности, как в известном анекдоте:

– Бабка, тебе дрова нужны? – обращаются к пожилой женщине молодые люди.

– Нет, сынки мои родимые, не нужны! – отвечает растроганная старушка.

На утро женщина обнаруживает, что с ее двора исчез весь запас дров...

Здесь, конечно, шутка, но логической ошибке, которая в ней обыгрывается, могут быть подвержены и вопросы, задаваемые вполне серьезно. Она состоит в двусмысленности вопроса и зависит от того, какие подразумеваются предпосылки:

1) Один смысл подразумевает предпосылку – «У Вас на дворе лежат дрова», а вопрос имеет смысл: «Нужны ли они Вам?»

2) Второй смысл. Предпосылка – «У Вас нет в запасе дров». Вопрос: «Нужно ли Вам привезти дров?»

Из предыдущих разъяснений относительно предпосылок ли-вопросов последние также, очевидно, не всегда бывают правильно поставленными. Так, в одном из известных логике софизмов некоторому человеку N адресуется вопрос «Перестал ли ты бить своего отца?» Предпосылка здесь «N перестал бить своего отца или не перестал». По-видимому, это – закон исключенного третьего, и потому ответом, как будто, должно быть «Перестал» или «Не перестал» (но в том и другом случае содержится признание N в том, что он бил своего отца). В действительности же эта предпосылка не является законом, ибо составляющие ее высказывания сформулированы неверно в том случае, если N не относится к числу людей, бивших своего отца. Ответом на этот вопрос могло бы быть: «Вопрос поставлен неправильно. Я не бил своего отца (то есть я не отношусь к области людей, к которым применим предикатор «перестал бить отца»)».

В заключение заметим, что ответ на правильно поставленный вопрос может быть полным или неполным, а также ответом по существу или не по существу (релевантным вопросу или не релевантным ему).

На вопрос «Какие существуют категории языковых выражений?» неполным, конечно, будет ответ «Имена» и даже «Имена и предложения». Полным ответом будет перечисление всех или, по крайней мере, основных категорий языковых выражений (см. § 6). Хотя отнюдь не всегда в ответ на вопрос «Какие?» возможно полное перечисление всех случаев, оно может быть практически даже невозможным. В таких случаях корректным является дополнение вопроса просьбой: «Приведите какие-нибудь примеры» или «Назовите то, что знаете» и т.п.

Ответ по существу таков, что он выясняет как раз то, что подлежит выяснению в формулировке самого вопроса. Конечно, на вопрос «Какая река является самым большим притоком Волги?» нерелевантным был бы ответ, что одним из ее притоков является Ока и тем более то, что Волга не впадает в Черное море.

Само собой разумеется, что ответ на некоторый вопрос может быть правильным или неправильным в зависимости от того, истинно или неистинно высказывание, в котором он выражается. Нетрудно усмотреть из определения вопроса, что если ответ на вопрос релевантен и правилен (хотя, возможно, даже не полон), то он должен включать информацию, заключенную в предпосылках, то есть предпосылки должны быть его следствиями.

Началом этого раздела уже был вопрос о предметном значении и смысле вопросительных предложений как одного из видов знаков (как одной из семантической категории знаков). Осуществленный здесь анализ вопросительных предложений приводит к заключению, что предметным значением вопроса является отсутствие некоторой информации в рамках некоторой имеющейся. Может возникнуть, правда, недоумение, как отсутствие чего-то может быть предметом мысли или предметным значением знака. На это, по-видимому, можно было бы ответить так: отсутствие чего-то вообще не может быть предметом мысли, но отсутствие чего-то в рамках наличия чего-то может быть таковым. Например, мы можем рассуждать о яме, колодце, хотя они представляют собой отсутствие земли в определенном месте, но при наличии ее вокруг. Что касается вопросов, то существенным для их определения является отсутствие информации именно в рамках какой-то имеющейся. Здесь уместным кажется вспомнить слова Гегеля: «Ничто от некоторого нечто есть определенное ничто». Вопрос как раз указывает на некоторое ничто (отсутствие информации) от некоторого нечто (в рамках какой-то данной информации). И это «определенное ничто» может быть предметом некоторой мысли и, следовательно, предметным значением какого-то знака.

 

Упражнения

 

Проведите анализ следующих вопросов (укажите, к каким видам они относятся, правильны ли они, каковы их предпосылки; дайте обоснование ответов):

1) Какие существительные не спрягаются?

2) Какие существительные не изменяются по падежам?

3) Для чего весной вспахивают поля?

4) Верно ли, что все студенты понимают то, что они говорят?

5) С какой скоростью движется Солнце в мировом пространстве?

6) Все ли корни уравнений являются целочисленными?

7) Кто придумал любовь?

8) Каким образом весна влияет на уравнения третьей степени?

• Гипотезой называют высказывание или теорию (совокупность определенных высказываний), представляющих собой некоторое предположение, то есть предположительный ответ на некоторый вопрос о существовании, о причинах какого-то явления и происхождении его и т.п.

Например, предположение – до полета спутника вокруг Луны – о существовании гор и кратеров на обратной стороне Луны; гипотеза А.И. Опарина о происхождении жизни на Земле, гипотеза о происхождении Солнечной системы и т.п.

Предположительный характер гипотезы означает, что она не является не только доказанной, но и не обоснована в такой мере, чтобы считаться практически достоверной. С другой стороны, научная гипотеза должна быть в той или иной мере обоснована: она должна быть согласована с имеющимися знаниями, фактами и, будучи выдвинутой для объяснения какого-то явления, она должна объяснять известные его стороны, характеристики и связи с другими явлениями.

Иметь гипотезы в качестве ответов на вопросы науки весьма полезно, даже если они мало обоснованы, поскольку они играют, по существу, ту же методологическую роль как и сами вопросы, на которые они отвечают. А именно, указывают направление научного поиска; но в отличие от вопроса гипотеза сужает это направление, конкретизирует его. Это происходит потому, что возникает возможность выведения следствий из гипотез, особенно следствий эмпирического характера, проверяемых путем наблюдения, эксперимента. Следствия именно указывают, в каком направлении должно осуществляться исследование для проверки их правильности. Они позволяют соответствующим образом организовать наблюдение, спланировать эксперименты. Таким образом, гипотеза стимулирует и направляет развитие знания. В связи с чем ее часто и характеризуют как форму развития знания. При этом подразумевается, очевидно, то, что называют гипотетико-дедуктивным методом познания. И гипотезы при этом, наряду с дедукцией, являются основными элементами этого метода (см. §§ 39, 42).

Когда речь идет о разрешении сложных вопросов науки, возникают различные, так называемые конкурирующие гипотезы, являющиеся различными ответами на одни и те же вопросы (ряд гипотез о происхождении Солнечной системы, имеются различные гипотезы о происхождении жизни, Вселенной и т.д.). При этом указанные выше требования согласованности гипотез с известными знаниями и фактами, способность их объяснять предъявляются к каждой из конкурирующих гипотез. Однако по мере развития знания какие-то из этих гипотез исключаются, поскольку перестают – по мере открытия новых фактов и расширения знания вообще – удовлетворять этим требованиям.

Среди конкурирующих гипотез предпочтение отдается обычно тем, которые дают более простые объяснения, содержат меньше недоказанных предпосылок, и тем более таким, которые позволяют предсказывать какие-то новые явления и их характеристики, то есть если можно так выразиться, обладают большим коэффициентом эвристичности. С логической точки зрения это означает, что эти гипотезы более информативны, дают возможность выведения из них более широкого круга следствий. И как уже было сказано при характеристике гипотетико-дедуктивного метода развития знания, гипотезы в процессе развития знания конкретизируются, совершенствуются, и «выживающие» в конкурентной борьбе становятся все более и более обоснованными.

Подчеркнутая выше направляющая роль гипотез, предварительных решений вопросов вообще, проявляется в том, что к таким предварительным решениям прибегают не только в научном познании, но широко применяют их в юридической практике. Подобное предварительное решение вопроса в оперативно-следственной, судебной практике называется версией. Иногда, правда, слово «версия» в юридической практике употребляют и в смысле «мнение», «точка зрения» участников юридического процесса (версия защиты и обвинения, версия истца и ответчика). В этом смысле «версия» уже не является, конечно, аналогом научной гипотезы.

 

ЛОГИКО-ЭПИСТЕМИЧЕСКИЕ И СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКИЕ АСПЕКТЫ АРГУМЕНТАЦИИ

Аргументация играет важную роль в процессах научного исследования, построения и развития теорий, в преподавательской деятельности, в процессах общения людей, в научных спорах и дискуссиях. В процессе аргументации осуществляется стремление к реализации одного из названных выше принципов логической правильности мышления – принципа достаточного основания (см. § 2).

В соответствии с ним мы можем принимать те или иные результаты научного познания – высказывания или теории – за истину лишь в том случае, когда либо имеем достаточные основания считать их таковыми, либо когда обоснование достигло такой степени, которая позволяет считать их практически достоверными. Указанные два случая, как разъяснялось раньше, различаются тем, что в одном мы имеем логически доказанные знания, а во втором – лишь практически достоверные. В соответствии с этим различаются и сами процессы аргументации – особо выделяются доказательства и опровержения – высказываний и теорий,– с одной стороны, и, с другой – подтверждение и критика (частичное опровержение) их.

Процессы аргументации, кроме того, имеют различные аспекты. В них играют роль как факторы логико-эпистемического характера, так и социально-психологического. Наконец, имеются различные формы самих аргументативных процессов: кроме элементарных форм – доказательств и опровержений, подтверждений и критики – имеются сложные формы – споры, дискуссии, представляющие собой определенное сочетание указанных элементарных форм.

Часть I. ЛОГИКО-ЭПИСТЕМИЧЕСКИЕ АСПЕКТЫ АРГУМЕНТАЦИИ

§ 45. Аргументация как прием познавательной деятельности. Виды аргументаций

• Аргументация – это форма мыслительной деятельности, цель которой состоит в обосновании утверждения об истинности или ложности некоторого высказывания или теории (или о принципиальной невозможности оценки высказывания как истинного или ложного, то есть бессмысленности его).

В процессе аргументации объектами нашего обсуждения выступают те или иные уже имеющиеся высказывания или теории. При этом в одних случаях истинность их предполагается, но требует обоснования, в других – высказывание или теория, выдвигаемые, например, оппонентом в споре или дискуссии – представляются ложными или даже бессмысленными, и требуется обоснование этого мнения. В простейших случаях истинность или ложность некоторого утверждения можно установить путем непосредственного обращения к фактам, однако, как правило, необходимы специальные логические процедуры, объединяемые под термином аргументации.

Есть существенная разница в обосновании высказываний и теорий. Вопрос об обосновании теорий относится к наиболее сложным и малоразработанным в логико-методологическом плане. Мы выделим его в особый раздел и рассмотрим первоначально процедуру аргументации применительно к высказываниям, как это обычно и имеется в виду в теории аргументации.

Обоснование высказывания может быть полным или частичным.

Полное обоснование утверждения об истинности какого-либо высказывания называется доказательством этого высказывания.

Полное обоснование утверждения о ложности какого-либо высказывания называется его опровержением.

Частичное обоснование утверждения об истинности некоторого высказывания называется его подтверждением.

Подтверждение, как мы уже говорили (см. § 39), есть особый прием обоснования высказываний. Возможны, конечно, различные степени подтверждения, и доказательство является предельным случаем подтверждения. Однако это такой предельный случай, который, как было также сказано ранее, в процессе подтверждения никогда не достигается. Подтверждение повышает степень вероятности того, что подтверждаемое утверждение истинно. Но эта вероятность может сколь угодно приближаться к 1, никогда, однако, не достигая ее. Вероятность, равную единице, дает нам только доказательство.

Когда речь идет о частичном обосновании утверждений о ложности некоторых высказываний, то здесь уместен термин критика (или частичное опровержение) соответствующих положений. Ясно, что она может быть также различных степеней и аналогично тому, как доказательство является предельным случаем подтверждения, опровержение есть предельный случай – также недостигаемый – критики высказывания.

 

46. Доказательство и опровержение

 

До некоторых пор мы будем пользоваться этим термином именно в этом – более широком – смысле и лишь при необходимости подчеркнуть некоторые особенности процесса опровержения будем выделять его как противоположность доказательству в узком смысле.

Кроме того, вместо точных, но довольно громоздких выражений «доказательство утверждения об истинности некоторого высказывания А» и «доказательство утверждения о ложности некоторого которого высказывания А» (без которых трудно было обойтись при точной формулировке общего понятия аргументации) будем теперь – с разрешения читателя – употреблять хотя и менее точные, но более удобные выражения: «доказательство истинности А» и «доказательство ложности А».

Состав доказательства (и, конечно, опровержения, поскольку речь идет о доказательстве в широком смысле). В доказательстве выделяются:

1. Тезис доказательства – высказывание, истинность или ложность которого доказывается.

2. Аргументы – высказывания, посредством которых осуществляется доказательство тезиса.

3. Промежуточные допущения – вспомогательные допущения, которые вводятся в процессе рассуждения (дедукции) и устраняются затем при переходе к окончательному результату рассуждения (См. «Непрямые правила», «Эвристические принципы введения допущений» §§ 10, 11.).

4. Форма доказательства – логический способ обоснования тезиса при помощи аргументов (возможно с использованием промежуточных допущений).

В доказательстве таким способом обоснования тезиса является дедуктивный вывод, то есть вывод, обеспечивающий истинность заключения (тезиса) при истинности посылок (аргументов доказательства). Основу такого дедуктивного рассуждения составляет совокупность принятых законов логики и правил перехода от одних высказываний к другим в процессе доказательства. Указание на характер этих переходов называют также демонстрацией (см. «Анализ доказательства», «анализ вывода» – §9).

Поскольку речь шла о доказательстве в широком смысле, приведенная характеристика состава доказательства относится и к доказательствам в узком смысле, а также и к опровержениям. Рассмотрим теперь более подробно элементы этого состава.

Поскольку доказательство – это рассуждение, завершающееся обоснованием тезиса, то форма доказательства – это форма соответствующего рассуждения – совокупность связей между исходными и возникающими в процессе рассуждения высказываниями. Если доказательство осуществляется в рамках некоторой логической системы, то форма его определяется совокупностью употребляемых в доказательстве законов и правил этой системы.

В процессе демонстрации происходит обоснование переходов от одних высказываний к другим и таким образом раскрывается характер упомянутых связей между высказываниями. Этот момент обоснования отсутствует в так называемых естественных рассуждениях, когда нет специального описания используемых в доказательстве логических средств.

Заметим, что в практике научного познания под термином доказательство имеют в виду не просто дедуктивный вывод тезиса из множества аргументов, а более широкую процедуру интеллектуального характера, включающую также и поиск аргументов. А это означает анализ некоторых известных связей, отношений в той области действительности, к которой относятся содержащиеся в тезисе утверждения. Так, доказательство равенства суммы углов треугольника 180° (в Эвклидовой геометрии) включает, как известно, определенное построение (проведение линии, параллельной одной из сторон треугольника) и анализ соотношений углов, образованных пересечениями этой линии двумя сторонами треугольника. В результате анализа оказывается, что в качестве аргументов здесь могут быть взяты уже доказанные теоремы о равенстве накрест лежащих углов, образуемых при пересечении двух параллельных третьей линией, и о равенстве развернутого угла 180°.

Существенную роль, так же в качестве аргументов, при этом играют, наряду с аксиомами, аналитически истинные утверждения, то есть утверждения, истинные в силу принимаемых определений. Такие, например, как «Развернутый угол – это угол, который образован двумя лучами, каждый из которых является продолжением другого» (оба луча составляют одну прямую).

Однако для представления доказательства в более полном виде в качестве аргументов могли бы быть взяты только аксиомы, которые были использованы в доказательстве упомянутых теорем, и высказывания, истинные по определению. Использование же ранее доказанных теорем – это способ сокращения доказательств.

Аргументы – в правильном доказательстве – это высказывания, истинность которых не вызывает сомнения, и при этом уверенность в их истинности имеет какие-то рациональные основания. Иначе говоря, аргументы – это такие высказывания, которые выражают знание человека о наличии или отсутствии соответствующих – утверждаемых или отрицаемых в этих высказываниях – ситуациях. Правда, у различных людей может быть различное отношение к одним и тем же высказываниям. Для одних – истинность высказываний очевидна, у других может вызвать сомнения. Это обусловливает необходимость учитывать при осуществлении доказательства и вообще в процессе аргументации – применяемой в процессе общения – характер аудитории, для которой она предназначена. Таким образом, в зависимости от аудитории правомерно употреблять в качестве аргументов то или иное множество высказываний. Различными также для разных аудиторий могут быть приемлемые законы логики и правила вывода. Представитель, например, интуиционистской или релевантной логики не признает некоторые способы рассуждения, приемлемые в классической логике.

Множество высказываний, приемлемых для данной аудитории в качестве несомненно истинных – для доказательства некоторого утверждения – или в качестве правдоподобных – когда речь идет лишь о более или менее достаточном подтверждении, а также совокупность приемлемых логических средств,– называется полем аргументации.

К числу несомненно истинных, или достоверных видов аргументов, входящих в поле аргументации, в любом случае обычно относят высказывания, истинность которых устанавливается на основе чувственного опыта при условии многократной проверки их с целью убеждения в надежности показаний органов чувств (во избежание случаев, когда мы имеем дело с оптическим обманом, миражом и т. п.).

Достоверными являются также утверждения, истинные по определению – аналитически истинные утверждения; далее, аксиомы содержательной теории, которые нередко даже и определяют в литературе как «утверждения, не требующие доказательства» («не требующие» – именно в силу их очевидности). Однако история науки знает немало примеров, свидетельствующих о том, что очевидность не всегда является достаточным критерием истинности.

Наконец, аргументами доказательства в составе некоторой теории могут быть утверждения, уже ранее доказанные в этой теории.

Промежуточные допущения играют вспомогательную роль. Они вводятся в зависимости от логической структуры тезиса и в конечном счете устраняются в процессе самого доказательства. Эти высказывания могут быть как истинными, так и ложными. Например, в доказательствах «от противного» вводятся – в качестве промежуточных допущений – обычно даже заведомо ложные высказывания.

 

Виды доказательств

Некоторым тривиальным и притом нелогическим, но играющим большую роль в познании видом доказательства является обоснование высказывания путем непосредственного обращения к фактам. Достаточным основанием для признания некоторого утверждения истинным или ложным в этом случае являются соответствующим образом проверенные показания органов чувств. Таким образом доказано, например, что существует смена времен года, дня и ночи, что иногда выпадают дожди, что существуют жидкие и твердые тела (а для удостоверения в существовании газообразных тел требуются некоторые дополнительные средства!).

Другой вид также тривиального, но уже логического характера является доказательство аналитически истинных высказываний. Доказательство их состоит просто в извлечении некоторой части информации, заключенной в некотором определении (дескриптивных или логических терминов). Например, для доказательства истинности утверждения, что все тела протяженны, мы можем просто обратиться к определению тела, согласно которому телом называют все то, что занимает часть пространства. Истинность утверждения, что у всякого параллелограмма противоположные стороны параллельны, следует прямо из определения параллелограмма как четырехугольника с параллельными сторонами. Из определения самоокупаемого предприятия и понятия рентабельности непосредственно по правилам логики, без учета каких-либо утверждений фактического характера, следует, что всякое рентабельное предприятие является самоокупаемым.

К сказанному – в соответствии с общепринятыми положениями – необходимо сделать добавление. Утверждение, выводимое из некоторого определения, может быть признано истинным лишь при условии доказанности существования объектов, вводимых определением. В противном случае, введя, например, термин «странная фигура» и определив его как «фигуру, являющуюся одновременно квадратом и кругом», мы могли бы доказать истинность утверждений: «Всякая странная фигура является квадратом» и «Всякая странная фигура есть круг».

Ясно что это замечание касается понятия аналитических суждений, если аналитичность, как это обычно делается, связывается с особым видом истинности (логической истинности). Необходимым условием признания в таком случае некоторого суждения аналитическим, кроме выводимости его из определения, является также непустота термина – субъекта этого суждения.

Логически сложные доказательства могут иметь различные виды в зависимости от характера аргументов, формы доказательства, от характера тезиса. Наиболее значимым является различение видов доказательств по двум последним основаниям.

Виды доказательств по характеру тезиса. Если мы хотим доказать истинность высказывания «Все S суть Р», то мы должны либо дедуктивно вывести его из других истинных общих суждений (Например, по модусу Barbara первой фигуры силлогизма (см. § 37).), либо установить посредством перечисления (в форме полной индукции), что каждый предмет из класса S обладает свойством Р, либо показать, что отрицание этого высказывания приводит к противоречию, либо установить, что свойство Sдетерминирует свойство Р, то есть доказать необходимость высказывания вида «Все S суть Р». В последнем случае мы доказываем, по существу, более сильное утверждение, а именно утверждение необходимого характера вида «Все S необходимо суть Р».

Для доказательства же ложности рассматриваемого высказывания, то есть для опровержения высказывания «Все S суть Р», достаточно указать хотя бы один случай, когда предмет из класса S не обладает свойством Р.

С доказательством истинности или ложности высказываний вида «Некоторые S суть Р» (существует предмет из класса S, обладающий свойством Р) дело обстоит двойственным (по отношению к высказыванию «Все S суть Р») образом.

Заметим, что некоторую особенность имеют доказательства истинности высказываний вида «Некоторые S есть Р» в логике и математике. Здесь доказательство истинности высказывания о существовании некоторых объектов осуществляется часто особым конструктивным образом – посредством указания способа построения (получения) этого объекта и обоснования того, что он удовлетворяет заданным условиям. Таково, например, доказательство существования наибольшего общего делителя некоторых двух чисел, наименьшего кратного для них; как помним, математика дает способ, аппарат, посредством которого в каждом случае мы можем указать искомое число, если оно действительно существует.

Особую значимость в науке имеют доказательства утверждений о наличии необходимых связей, каковыми собственно и являются законы науки. Однако с ними связаны и особые трудности. Мы уже упоминали, что доказательство истинности утверждения «Все S суть Р» можно получить из доказательства истинности высказывания «Свойство S детерминирует свойство Р». (Утверждения о детерминированности одного свойства другим или одного явления другим представляют высказывания необходимого характера. Детерминированность составляет основное содержание законов науки.)

Для доказательства утверждения «Всякое число, которое оканчивается на 5 (в десятичной системе), необходимо делится на 5», достаточно показать, что число, оканчивающееся на 5, может быть представлено как сумма чисел, в каждом слагаемом которой имеется делитель 5, и использовать известное положение арифметики о том, что число, являющееся делителем каждого члена суммы (в данном случае 5), является так же и делителем самой суммы.

Вообще, в доказательствах утверждений о наличии необходимых связей большую роль играет, как мы уже говорили, метод научных объяснений (см. § 43) и употребляемые в связи с ним предложения соответствия (см. § 42), но для них, как и вообще для объяснительных теорий, не существует строгих методов доказательств. Возможно установление лишь практической достоверности их посредством многочисленных подтверждений. В целом, проблема доказуемости теорий является одной из наиболее сложных и не разработанных в логике и философии (см. § 42).

Виды доказательств по форме. Основными видами доказательств, различающихся по форме, являются доказательства прямые и непрямые (косвенные).

Прямые доказательства представляют собой дедуктивный вывод, в котором тезис непосредственно выводится из аргументов в качестве заключения вывода.

Непрямое доказательство (истинности или ложности) высказывания А (тезиса) состоит в том, что оно достигается посредством опровержения некоторых других высказываний. Здесь выделяются два вида непрямых доказательств: доказательство «от противного» (апагогическое) и доказательство посредством исключения альтернатив.

Доказательство «от противного», осуществляется посредством применения непрямого правила рассуждения:

 

 

Для доказательства истинности А при наличии множества аргументов Г предполагается ложность этого высказывания (истинность ) и показывается, что из Г и этого предположения выводимо противоречие:  Указанное правило позволяет заключить при этом, что из аргументов Г выводимо А.

Здесь мы, очевидно, употребляем термин «доказательство» в узком смысле – как противоположность опровержению. Известна также форма непрямого опроверженияА (доказательство ), осуществляемое по правилу:

 

 

Опровержение этого рода характеризуется как опровержение путем сведения к абсурду.

Доказательства «от противного» известны, очевидно, всем из школьных курсов по математике. Заметим, однако, что там они описываются так, что в них нелегко усмотреть приведенную только что форму рассуждения. Обратимся к одному из таких описаний:

Этот способ доказательства состоит в том, что мы делаем сначала предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждения, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.

 

 

По существу, в любом доказательстве «от противного» мы имеем в качестве его составной части и указанную выше форму опровержения путем «сведения к абсурду». Именно: мы получаем сначала

 

 

Доказательство посредством исключения альтернатив состоит в том, что, например, для доказательства того, что некоторый проступок совершил Петров, мы используем в качестве аргумента дизъюнктивное высказывание (перечисление альтернатив): «Этот поступок совершил Иванов или Сидоров, или Петров», а также знание (которое составляет другие аргументы), что Иванов не совершал и Сидоров не совершал этого проступка. Отсюда, исключая первые два члена из приведенной дизъюнкции, получаем заключение: «Проступок совершил Петров». Обобщенная форма подобных доказательств такова:

 

 

Ясно, что условием истинности дизъюнктивного аргумента А₁, ..., А_т является перечисление именно всех возможностей, среди которых и тезис, и все его возможные альтернативы.

Данное правило рассуждения, лежащее в основе непрямого доказательства посредством исключения альтернатив, является, как мог заметить внимательный читатель, обобщением известной дедуктивной формы дизъюнктивного силлогизма Modus tollendo ponens (см. § 35):

 

 

Аргумент A₁ v ... v A_m, указывающий на все альтернативы, получается зачастую как результат деления объема некоторого понятия. Например, если мы знаем, что простые суждения бывают единичные, частные и общие, то отсюда получаем дизъюнктивное высказывание: «Некоторое данное простое суждение является единичным или оно является частным, или оно является общим». Если установлено теперь, что оно не единичное и не общее, то в качестве заключения имеем утверждение, что данное суждение является частным.

Рассмотренный способ доказательства, согласно свидетельству А. Конан-Дойля, служил основным методом Шерлока Холмса. На вопрос, в чем суть его дедуктивного метода, Шерлок Холме отвечал: «Установите все возможности, относящиеся к исследуемому событию, затем исключите последовательно все их, кроме одной, тогда это последнее и будет служить ответом на интересующий вас вопрос!»

Указанное – традиционное – деление доказательств на прямые и непрямые (косвенные) не является достаточно точным, поскольку как в той, так и в другой форме доказательства тезис, в конечном счете, является заключением дедуктивного вывода. Более строгим образом следовало бы разделять доказательства на прямые и косвенные в зависимости от того, используются ли в качестве посылок вывода только аргументы или также и вспомогательные допущения. В последнем случае доказательство является косвенным, поскольку в нем применяются непрямые (косвенные) правила вывода (см. § 10).

Подтверждение и критика (тезиса)

Как уже неоднократно отмечалось, отнюдь не всякое истинное утверждение не только повседневной жизни, но и научного познания, может быть строго доказано (а ложное – опровергнуто). В этом отношении характерны утверждения философии. По самому характеру этой науки ее высказывания носят весьма общий характер. Поэтому доказательства их в строгом смысле просто невозможны. Принципиально невозможно ни доказать, ни опровергнуть идеалистическое или материалистическое понимание мира (мир существует объективно, независимо от сознания, какого-либо духа, идеи или, наоборот, что он является порождением мирового духа, абсолютной идеи или даже сознания человека). Неоднократно предпринимались, но всегда оказывались неудачными, попытки доказать или опровергнуть утверждения о конечности или бесконечности мира во времени и пространстве (В связи с последними высказываниями возникает даже проблема, связанная с проблемой истины. Согласно этому понятию, как уже говорилось (см. § 1), некоторое высказывание истинно, если, и только если, ситуация, которую оно описывает, существует в действительности. Но как быть с ситуациями, представляющими собой те или иные характеристики самого мира?).

• Наиболее распространенной формой аргументации как во многих науках, так и в повседневной жизни, является подтверждение или критика тех или иных утверждений.

Подтверждение и критика тезиса имеют тот же состав, что и доказательство и опровержение, но отличаются они, соответственно, от строгих доказательств и опровержений либо недоказанностью аргументов, либо применением недедуктивных способов рассуждения, то есть таких способов рассуждения, которые не обеспечивают истинности заключения даже при доказанной истинности посылок.

Множество примеров подтверждения первого рода существует в естественных науках. Один из них – подтверждение гипотезы В. Паули о существовании микрочастиц нейтрино. Гипотеза возникла в связи с тем, что при явлении известного в физике бета-распада наблюдение приводило к выводу о том, что бесследно исчезает некоторая часть энергии, выделяемой при распаде. Суть гипотезы состояла в том, что эту «исчезающую» часть энергии уносят частицы, которые и были позже названы «нейтрино» (которые не удавалось никаким образом обнаружить). Основным аргументом в пользу данной гипотезы служило известное положение о том, что энергия не может исчезать бесследно, то есть закон сохранения энергии. Однако сам этот закон, хотя и является практически достоверным (достигшим высшей степени подтверждения), не был тем не менее логически доказан.

Примеры подтверждения второго рода связаны с рассмотренным выше гипотетико-дедуктивным способом рассуждения, в котором применяются правдоподобные рассуждения «от следствий к основанию», то есть такой способ рассуждения, при котором повышение вероятности истинности гипотезы достигается накоплением информации за счет доказательства или подтверждения вытекающих из нее следствий. Однако нередко здесь могут быть использованы и такие формы правдоподобных рассуждений, как аналогия и неполная индукция.

Как уже отмечалось, степень подтверждения может оказаться настолько высокой, что теория практически будет считаться достоверной. Аналогично дело обстоит и со многими отдельными утверждениями науки.

КРИТИКА ДОКАЗАТЕЛЬСТВ И ОПРОВЕРЖЕНИЙ

Следует иметь в виду, что термин «опровержение» нередко употребляется в двух смыслах: 1) в том смысле, который был указан выше,– как полное обоснование ложности некоторого высказывания; 2) как процедуру выявления ошибочности построения некоторого доказательства или подтверждения (обоснования вообще) истинности или ложности некоторого утверждения.

Во избежание этой двусмысленности для процедуры выявления ошибочности некоторого обоснования целесообразно принять термин «критика» (имея в виду критику того или иного процесса обоснования некоторого высказывания).

Специально обратим внимание читателя на то, что критику некоторого процесса обоснования нельзя смешивать с критикой тезиса, который подлежит обоснованию.

Критика некоторого процесса обоснования – это выявление (критика) ошибок в его построении. Поэтому характер этой процедуры выясняется, по существу, в связи с разбором возможных ошибок в доказательстве (см. § 49). Здесь же укажем, во-первых, на то, что критика связывается с основными частями обоснования. Она может относиться к тезису, аргументам и форме доказательства. Во-вторых, отметим,

что выявление ошибок в процессе обоснования некоторого тезиса отнюдь не указывает на несостоятельность самого тезиса.

ВОПРОС ОБ ОСНОВАНИИ ТЕОРИЙ

Прежде всего надо заметить, что здесь лишь в некоторых особых случаях мы можем достигать полных обоснований, то есть доказательств теории. Это относится лишь к некоторым теориям методологического характера, цель которых состоит в выработке методов решения каких-то задач. К их числу относятся определенные логические и математические теории. Доказательство истинности некоторой, например, теории дедукции или логического исчисления состоит в том, чтобы показать, что каждая теорема этой системы является законом данной системы, общезначимым высказыванием.

Однако основной формой обоснования теорий является не доказательство их, а подтверждение, то есть обоснование с той или иной степенью полноты. И при этом главным методом обоснования является описанный выше гипотетико-дедуктивный способ обоснования. Сама процедура обоснования при этом состоит, напомним, в выведении такого рода следствий из теории, истинность которых может быть доказана опытным путем. Однако научная добросовестность ученого проявляется в том, что он ищет не только то, что подтверждает его гипотезы, но и то, что может их опровергнуть. И последнее иногда даже в первую очередь.

Но самый основной и обычно первоначальный шаг в обосновании каждой теории состоит в установлении ее непротиворечивости, В аксиоматических теориях – непротиворечивость системы ее аксиом или, говоря более обобщенно, в невозможности вывода из ее аксиом какой-то формулы А и одновременно ее отрицания  В теориях гипотетико-дедуктивного типа необходимо убеждение в том, что не противоречивы, согласуются между собой, по крайней мере, ее основные, исходные положения. Только после того, как имеется убеждение в том, что теория является непротиворечивой, приобретают смысл все описанные выше процедуры ее подтверждения.

 

Правила и возможные ошибки в процедурах обоснования

Имеется ряд правил построения процедур обоснования. Они связаны с основными частями этой процедуры: с тезисом, с аргументами, формой обоснования. Сами по себе эти правила довольно тривиальны, но их формулировка предназначена для того, чтобы предупреждать некоторые типичные ошибки логического характера, встречающиеся в аргументации, которые являются уже отнюдь не тривиальными.

ПРАВИЛА ПО ОТНОШЕНИЮ К ТЕЗИСУ

1. Тезис должен быть ясно выделен и сформулирован точным образом, то есть должно быть точно сформулировано подлежащее обоснованию суждение.

Условия точности формулировки суждения мы уже разбирали (см. § 29). Не мешает напомнить, что точность формулировки суждения означает явное указание всех его смысловых аспектов:

– если суждение простое, то должны быть выделены его логические подлежащие (субъекты) и логическое сказуемое (предикат);

– если какой-то из субъектов представлен общим именем, то нужны его точные количественные характеристики («Все» или «Некоторые»);

– ясными должны быть также модальные характеристики суждения (см. § 33);

– при формулировке сложных суждений должен быть понятен логический характер объединяющих их логических связок;

– и, конечно, необходима достаточная ясность употребляемых в суждении понятий, связанных с его дескриптивными терминами (см. 6) и т.д., и т.п.

Короче говоря, тезис не должен быть двусмысленным и неопределенным по смыслу.

В связи со сказанным очевидны теперь и возможные ошибки, представляющие собой нарушение этого правила. Они могут состоять как раз в том, что тезис сформулирован нечетко, не определяет точно, что подлежит обоснованию или допускает различные истолкования. Примером такого тезиса может быть утверждение «Капитализм лучше социализма» (или наоборот): одно может быть лучше или хуже другого в разных отношениях – в экономическом, социально-политическом, духовном, этическом и т.д. отношениях.

Другой пример неясного тезиса: «Животные, например, собаки «не знают» законов природы». Неясность состоит в неоднозначности того, что значит «знают»: 1) означает ли это, что они не могут их сформулировать в языке или 2) они не умеют использовать их в своем поведении. Если иметь в виду второй смысл, то есть принять номинальным образом такое определение термина, тогда мы должны согласиться и с тем, что собака не знает, что годится ей в пищу, не знает, как поступить при появлении угрозы ее жизни, не знает даже своего хозяина... Мы хотим обратить здесь внимание на то, что истинность или ложность тезиса зависит от определений имеющихся в нем слов. Но выбор определений в процессе аргументации не является, конечно, абсолютно произвольным; как мы видим, это может приводить нас к явному конфликту с общепринятыми положениями.

Наконец, нельзя доказывать или опровергать то, что связано с индивидуальными вкусами людей, нелепо, конечно, было бы выдвигать на обсуждение тезис: килька в томате лучше кильки в масле.

2. Второе правило состоит в том, чтобы тезис оставался тождественным, то есть тем же самым, на протяжении всего процесса обоснования: он не должен изменяться, по крайней мере, без специальных оговорок.

В процессе аргументации может возникать необходимость в каком-то уточнении, конкретизации тезиса и вообще внесения каких-то поправок в исходное положение, но все такие коррективы должны быть точно фиксированы.

Рассмотренные правила, очевидно, связаны между собой: чем менее четко сформулирован тезис, тем больше возможность его подмены. Типичной ошибкой, возникающей в результате нарушения этого правила является подмена тезиса. Подмена осуществляется часто так, что доказывается нечто одно, по-видимому близкое к тезису, а в результате это выдается за доказательство тезиса. Причем это происходит зачастую за счет подмены понятий.

Положим, в суде доказывается виновность определенного человека в совершении преступления. Однако прокурор вместо этого доказывает, что данный человек совершил этот проступок (известно, что виновность в совершении некоторого действия состоит не в самом факте его осуществления, но включает также ряд моментов социально-психологического характера: способность или неспособность предвидения последствий проступка, наличие или отсутствие намерений вызвать эти последствия и т.д.). Если же при этом адвокат доказывает, что человек не совершал этого проступка, то тем самым он доказывает утверждение более сильное, чем нужно (поскольку из него следует уже невиновность). В таких случаях подмены тезиса говорят: «Человек доказывает слишком много». Хотя подмены такого рода менее грешат против логики, тем не менее и они нежелательны, потому что дают возможность противнику в споре легче опровергнуть то, что доказывают, и при этом часто под видом опровержения выдвинутого тезиса.

При анализе рассмотренного примера мы выделили две разновидности подмены тезиса: подмена его более слабым в рассуждениях прокурора и более сильным в доказательстве адвоката.

Возможно, однако, и третье – когда вместо данного тезиса доказывается утверждение, просто нерелевантное ему. Дополняя данный пример, можно было бы привести выступление какого-либо общественного защитника, который рассуждал бы, положим, так: «Этот человек не является виновным, наоборот, он является добрым, вполне порядочным и очень добросовестным работником».

Вероятно, в судебной практике такого рода ошибок не происходит. Иначе, это бы означало, что адвокатам и прокурорам не известно понятие виновности. А пример этот надо рассматривать просто как модель возможных ошибок такого рода.

Если вспомнить основные принципы правильного мышления (см. § 2), то можно сказать, что подмена тезиса в доказательстве – это нарушение принципа последовательности и, в свою очередь, как правило, принципа определенности. Мы обращаемся к этим принципам здесь не случайно. Они в определенной форме закреплены даже в судебном законодательстве.

Естественно, что к числу ошибок подмены тезиса должны относиться случаи, когда критика доказательства, выявление несостоятельности его в тех или иных пунктах выдается (или воспринимается) за опровержение тезиса: истинность или ложность тезиса не зависит от того, правильно или неправильно осуществляется его обоснование.

ПРАВИЛА ПО ОТНОШЕНИЮ К АРГУМЕНТАМ

1. Аргументы должны быть истинными утверждениями.

2. Более того, при построении доказательства аргументы должны быть доказаны.

В процедурах подтверждения – в какой-то мере обоснованы, не исключая, конечно, при этом и возможность их доказанности. Если аргументация применяется в процессе спора, дискуссии, то аргументы должны быть, по крайней мере, приемлемы для их участников, то есть должны быть элементами принятого поля аргументации.

3. Доказательство или подтверждение аргументов, которые могут сопутствовать основному процессу аргументации, должны осуществляться независимо от тезиса (автономность обоснования аргументов).

Ошибочными согласно этим правилам надо считать доказательства, в которых используются ложные или хотя бы даже не доказанные аргументы. Для подтверждения неподходящими являются аргументы, не обоснованные в такой степени, что нет уверенности в их истинности. Например, Аристотель утверждал, что причиной падения тел на Землю является их стремление к естественному месту. Здесь подразумевался ложный аргумент: для всякого тела имеется некоторое естественное место, к которому тело стремится.

Явно ложный аргумент используется в рассуждениях следующих типов, с которыми каждому в жизни нередко приходилось, наверное, встречаться. Человек возмущается, что после починки у его ботинок стали очень высокими каблуки. Мастер отвечает: «Что же Вы, предпочитаете совсем без каблуков ходить?» Вы упрекаете кого-то, что тот ответил кому-то довольно грубо. Он возражает: «Что ж по Вашему, я лебезить перед ним должен?» Ошибку такого рода можно охарактеризовать как из крайности – в крайность иногда ее называют «дамский аргумент». В этих рассуждениях, по существу, используются ложные дизъюнкции вида А или В, где А и В –противоположности (крайности), между которыми есть промежуточные возможности, а рассуждающий склонен считать, что таковых нет.

Бывает так, что какой-то человек высказал о другом положительное мнение, имея в виду, положим, его нравственные качества, в другом случае – отрицательное по поводу его профессиональных способностей. Человеку, обвиняя его в непоследовательности, ставят вопрос: «Когда же Вы сказали правду?», умышленно или неумышленно подразумевая ложную (строгую) дизъюнкцию: либо одно верно, либо другое, улавливая лишь то, что одно высказывание характеризует человека положительно, а другое – отрицательно, и как таковые эти характеристики, конечно, несовместимы между собой.

К числу ошибок, связанных с ложными аргументами, относится также ошибка, которую характеризуют как употребление аргумента, который доказывает слишком много. Это случай, когда ложность аргумента сама по себе не очевидна, но обнаруживается, что, применяя этот аргумент, можно доказать не только выдвигаемый тезис, но и нечто явно ложное. Например, во время дискуссий о необходимости запрещения пропаганды войны некоторые их участники выдвигали тезис о том, что нельзя запрещать пропаганду войны, поскольку это означало бы ограничение демократического принципа свободы слова. Иные по поводу этого аргумента возражали так: «При таком понимании свободы слова, которое здесь имеется в виду, не следовало бы запрещать также и призывы к убийствам тех или иных людей, к совершению террористических актов, диверсий и т.п.». Однако такого рода запреты имеются даже в самых демократических государствах. Это указывает на то, что выдвигаемый аргумент при соответствующем – подразумеваемом – понимании свободы слова (как абсолютной свободы) является явно ложным.

Явно несостоятельными являются доказательства, в которых, кроме обоснования самого тезиса, содержится обоснование какого-либо из аргументов и в этом последнем используется сам тезис. Эта ошибка носит название круг в доказательстве. Например, ученик утверждает, что число 10⁶ является натуральным (тезис). Аргументы: «Оно является членом натурального ряда, а всякий член натурального ряда есть натуральное число». Но на вопрос о том, откуда видно, что оно является членом натурального ряда, следует ответ; «Это ясно из того, что число это является натуральным!» Иначе ошибку этого типа характеризуют иногда так: То же через то же.

Другая ошибка, связанная с нарушением правила автономности обоснования аргументов называется предвосхищение тезиса – petitio principii (буквально: предвосхищение основания). Она состоит в том, что в качестве аргумента в доказательстве используется утверждение, обоснование которого неявно предполагает уже истинность тезиса. Когда использование тезиса для обоснования такого аргумента выявляется, то есть становится явным, то возникает «круг в доказательстве». Такой аргумент представляет собой либо некоторую замаскированную переформулировку тезиса, либо, будучи сложным высказыванием, содержит тезис в качестве своей составной (конъюнктивной) части. Так, некоторые философы, например, доказывали, что мир имел начало во времени, аргументируя («от противного») так: «Если бы мир не имел начала во времени, то это означало бы, что к настоящему времени была бы отсчитана бесконечность. Но бесконечность нельзя отсчитать. Следовательно, мир имел начало во времени». В аргументе «В случае бесконечности мира во времени была бы отсчитана бесконечность» содержится как раз утверждение о том, что мир имел начало во времени. Ибо само понятие «отсчитано» указывает на то, что имеется начало и конец отсчета. Очевидно, что в таких случаях, как и в случае «круга в доказательстве» имеется ошибка необоснованный аргумент.

 

 

Примеры

 

1. Из области теологических споров. Все теологи утверждают, что Бог всемогущ. Если Бог всемогущ, то Он может создать камень, который не может поднять. Но если он не может сделать что-то, то Он не всемогущ. Значит, если Бог всемогущ, то Он не всемогущ. Следовательно, Он не всемогущ.

Заключение было бы истинным при истинности используемых аргументов. Однако, поскольку существование Бога недоказано, то утверждения о нем (как раньше уже подчеркивалось относительно утверждений такого рода) не имеют реального содержания, то есть не имеют смысла в строгом смысле этого слова (см. § 6). Тем же людям, кто верит в существование Бога, необходимо, очевидно, уточнить, что значит его Всемогущество.

2. Из логической практики. Еще со времен Древней Греции известен так называемый парадокс «Лжец»: один критянин заявил, что все жители острова Крит – лжецы (в том смысле, что всегда говорят ложь). Если он сказал правду (то есть действительно, все критяне – лжецы), тогда и он лжец и, следовательно, сказал неправду (то есть неверно, что сказал правду). Таким образом, оказывается, что если упомянутый человек сказал правду, то он сказал неправду. Отсюда следует, что он сказал неправду (конечно, если истинно, что он вообще говорил то, что ему приписывается).

А. Эйнштейн в книге «Сущность теории относительности» (1955 г.) замечает: «Уязвимым местом принципа инерции было то обстоятельство, что он содержал логический круг: масса движется без ускорения, если она достаточно удалена от других тел; но мы знаем о ее достаточной удаленности от других тел только по ее движению без ускорения».

Точнее надо было бы сказать, что здесь содержится ошибка petitio principii и то лишь при определении,– которое имеет в виду А. Эйнштейн,– высказывания «масса (тела) находится на достаточно большом расстоянии от других тел», если и только если (по определению) «она не испытывает гравитационного воздействия от этих тел». Однако возможно и другое определение, согласно которому «тело находится на достаточно большом расстоянии от других тел, если, и только если, оно удалено от них на некоторое расстояние n, положим, не менее 100 км». Аргумент «тело находится на достаточно большом расстоянии от других тел» в сочетании с тем, что на тело не действует непосредственно никакая сила – вроде двигателя космического корабля – доказывает, что это тело движется без ускорения.

Указанное расстояние можно, очевидно, определить более или менее точно, удаляя тело от других тел настолько, чтобы прекратилось, практически по крайней мере, гравитационное воздействие других тел на него. Кажется, что в таком случае снова возникает ошибка «круга в доказательстве». Однако понятие гравитационного воздействия мы используем здесь для образования некоторого общего понятия, равнозначного понятию «тело, находящееся на достаточно большом расстоянии от других тел». Это общее понятие сформулировано уже в других терминах, хотя и с учетом, конечно, понятия гравитации, и, применяя его в некотором конкретном случае для доказательства того, что какое-то тело движется равномерно, то есть не испытывает гравитационных воздействий от других тел, мы не допускаем уже указанной ошибки (Здесь применяется один из методов познания, который К. Маркс назвал «оборачиванием метода».).

В процессе познания часто встречаются мнимые «круги». И нужна определенная осторожность, чтобы не принимать их за действительные. Мы определяем, например, общее понятие скорости, пользуясь понятием путь, а именно, как путь, пройденный за единицу времени. Однако в конкретных случаях мы доказываем, что путь, пройденный данным телом, равен S, используя в качестве аргумента закон механики S = v • t (для равномерных движений). Здесь нет круга, если значение скорости v, в этом именно случае, не определяется через значение пути S. Между тем рассматриваемая ситуация еще более похожа на круг, чем в примере Эйнштейна, поскольку понятие пути непосредственно используется в определении общего понятия скорости.

ПРАВИЛО ОТНОСИТЕЛЬНО ФОРМЫ ДОКАЗАТЕЛЬСТВА

Это правило состоит просто в том, что рассуждение в доказательстве должно быть логически правильным: в доказательстве тезис должен следовать из аргументов. Или – в случае подтверждения – аргументы должны подтверждать тезис, то есть повышать степень вероятности его истинности.

Когда в доказательстве тезис не следует из аргументов, ошибка так и называется не следует – nоn sekietur. В случае же, если аргументы не повышают степень вероятности истинности тезиса – в процессе подтверждения,– ошибку можно назвать по аналогии с предыдущей не подтверждает.

ПРИМЕРЫ ОШИБКИ «НЕ СЛЕДУЕТ»

1. Адвокат пытается доказать, что подсудимый не совершал вменяемое ему преступление, рассуждая так: «Если бы обвиняемый был богат, то этот автомобиль он купил бы. Если ж обвиняемый был бы бесчестен, то он украл бы его. Однако обвиняемый не богат и уж ни в коем случае его нельзя отнести к бесчестным. Следовательно, обвиняемый не покупал и не крал этого злополучного автомобиля».

Установите, какая форма вывода использована и в чем состоит логическая ошибка?

2. Некто утверждает, что Иванов не слесарь, поскольку известно, что он токарь, а токарь не есть слесарь. В данном случае также имеем ошибку «не следует»: из того, что Иванов токарь, а профессия слесаря отличается от профессии токаря, не следует, что Иванов не может иметь эту последнюю. Видимость следования имеет здесь место из-за смешения понятий «человек, обладающий некоторой профессией» (конкретное понятие) и «профессия некоторого человека» (абстрактное понятие). В результате подмены напрашивается ложный аргумент: «Тот, кто обладает профессией токаря, не обладает профессией слесаря».

3. Читатель сам, вероятно, поймет теперь, в силу чего имеет место ошибка «не следует» в аргументации: «Древние греки внесли большой вклад в развитие философии. Спартанцы – древние греки, следовательно, они внесли большой вклад в развитие философии».

Вспомните о различии между общим понятием и единичным именем, обозначающим его объем, рассматриваемый как самостоятельный объект мысли (см. § 6).

Наконец, распространенной в аргументации является ошибка аргумент к человеку («довод о человеке» – argumentum ad hominem). Ее относят часто к числу ошибок, связанных с аргументами, а иногда связывают с тезисом. Она действительно некоторым образом связана и с аргументами, и с тезисом, но, по существу, это, скорее, ошибка, относящаяся к форме (демонстрации) доказательства. Она возникает в особых случаях, когда тезис связан тем или иным образом с каким-то лицом, и состоит в том, что в качестве аргументов используются те или иные характеристики этого лица, от которых зависит доверие или недоверие к тезису, но вывод при этом делается об истинности или неистинности тезиса.

Например, при доказательстве виновности или невиновности человека выдвигается в качестве аргумента то, что он является честным, добропорядочным или, наоборот, лжив, имеет преступные наклонности и т.п. Сами по себе эти аргументы, возможно, истинны (поэтому нет ошибки, связанной с аргументами), но из них не следует то, что требуется доказать. Правда, если истинность таких аргументов выдают за доказанность тезиса, тогда возникает ошибка подмены тезиса.

Истинность или ложность некоторого утверждения, высказанного каким-то ученым, пытаются иногда обосновать ссылкой на его авторитет, компетентность, научную добросовестность... Однако истинность или ложность суждений в силу самих определений этих понятий (см. § 1) не зависит ни от каких качеств тех, кто высказывает эти суждения. Авторитет лица, которому принадлежит некоторое утверждение, может порождать доверие к этому утверждению и даже безусловную веру в его истинность. Но вера, доверие – это психологические понятия, тогда как истина, ложь, доказанность, опровергнутость, обоснованность вообще – это понятия логики и эпистемологии.

Есть примеры неверной аргументации, ошибочность которых связана одновременно и с аргументами и с формой доказательства таким образом, что трудно выделить конкретно, к какой именно части аргументации относится ошибка. В таких случаях полезно использовать некоторые приемы опровержения без этой конкретизации и детализации – мы просто можем установить неправильность рассуждения. Об одном из таких приемов мы уже упоминали – это опровержение с использованием аналогии рассуждений (см. § 39). Положим, кто-то обосновывает тезис, что язык, наряду с формами мысли и рассуждений, также является предметом изучения логики, поскольку изучаемые ею формы и приемы мышления выражаются в языке. По аналогии этому рассуждению мы можем противопоставить такое: «Для историков, которые изучают документы периода существования СССР, предметом изучения является и язык, поскольку изучаемые документы зафиксированы в языке».

Неправильность этого рассуждения очевидна. Мы видели выше, что логика действительно изучает язык, но с определенной точки зрения – как средство познания. И отнюдь не в силу того, что формы и законы, которые она изучает, фиксируются в языке. Таким образом, мы здесь критикуем не тезис предполагаемого автора, а способ его обоснования.

СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКИЕ АСПЕКТЫ АРГУМЕНТАЦИИ

В связи с ошибками типа «к человеку», «к авторитету» в нашем изложении наметился выход за пределы логико-эпистемических аспектов аргументации. Здесь затрагиваются уже факторы социально-психологического характера. Факторы такого рода и связанные с ними аспекты аргументации также существенны для понимания возможных ошибок в аргументации. С ними также связаны определенные принципы, правила аргументации. Во избежание упомянутых ошибок, например, ошибки обращения к авторитету, полезно иметь в виду принцип, что в процессе познания на мир надо смотреть своими глазами, а не через призму тех или иных концепций, сложившихся взглядов на мир. Человек иногда развивает какую-то философскую или специально-научную мысль по тому или иному вопросу и среди слушателей обычно находится кто-то, категорически требующий ответов: «А в соответствии с кем? Кому Вы следуете – Канту, Гегелю или Марксу?», «Это что, по Бору, Гейзенбергу или по Эйнштейну?» Спрашивающий явно уверен, что на мир обязательно надо смотреть с точки зрения той или иной уже готовой концепции (не учитывая того, что авторы этих концепций имеют их именно потому, что действовали не в соответствии с такими установками!). Конечно, решая тот или иной вопрос науки или практической жизни, полезно и даже необходимо знать хотя бы основные результаты предшествующих поисков. Но полезно это именно потому, что дает возможность быстрее и более четко увидеть в самой реальной действительности то, что составляет их рациональное содержание. Учесть имеющиеся объяснения рассматриваемых явлений полезно опять-таки для того, чтобы объективным образом составить собственное представление о них. Настоящее понимание тех или иных положений науки заключается в том, что зафиксированные в них связи и отношения действительности усматриваются в самой этой действительности. Когда человек хорошо усвоил те или иные научные результаты, у него возникает чувство, что он мог совершенно свободно придти к ним и самостоятельно. Но богатство мира не исчерпывается, конечно, никакими концепциями, а наличие различных решений одного и того же вопроса указывает и на то, что в них имеется что-то неверное или неточное. Составить свое мнение о действительности, наряду с существующими концепциями, должно означать как раз преодоление указанных недостатков с сохранением, конечно, и их рациональных моментов. И совсем уж нелепо, когда критики упомянутого типа в таких случаях упрекают авторов в том, что у них имеется «смешение различных концепций».

Наиболее важным принципом аргументации надо считать, очевидно, и требование научной добросовестности и объективности в оценке тех или иных теорий. Это требование состоит в необходимости – при доказательстве или опровержении, в попытках подтверждения или критики обсуждаемого тезиса – отвлекаться от приверженности к тем или иным концепциям, от симпатий или антипатий в отношении автора выдвигаемого тезиса, от собственного честолюбия или самолюбия. Ничто не должно затмевать основную задачу аргументации – выяснение истинности или ложности обсуждаемого материала, и нельзя позволить себе уходить от решения именно этой задачи.

Требование научной добросовестности, научной объективности, например, ученого, занятого обоснованием выдвигаемого им решения какого-то научного вопроса, состоит как раз в том, чтобы, пытаясь обосновать истинность предлагаемого решения вопроса, автор, наряду с попытками его доказательства, должен искать также, и скорее даже в первую очередь, его возможные опровержения. В таких случаях, как легко заметить, происходит как бы «раздвоение личности». Оно выражается в том, что автор одновременно выступает и как защитник тезиса и как оппонент, пытающийся его опровергнуть (сравните случаи, когда человек спорит сам с собой; это весьма полезное раздвоение личности в отличие от известного болезненного психического ее раздвоения). Это, если можно так выразиться, монологическая форма спора. В процессе же общения она переходит в диалогическую форму аргументации, то есть превращается в более сложный аргументативный процесс, называемый спором в собственном смысле слова.

Спор и дискуссия как разновидности аргументации. Виды споров

В ходе спора, дискуссии взаимно дополняют друг друга два вида деятельности: доказательство некоторого тезиса одним лицом или, возможно, группой лиц и опровержение тезиса другим лицом или другими лицами. Но так или иначе в споре участвуют, по крайней мере, два лица: пропонент и оппонент.

В массовых спорах наиболее часто выступает один – пропонент, выдвигающий тезис,– против многих оппонентов. Таким образом происходят дискуссии на семинарах, при обсуждении докладов. При этом тезис не состоит из одного только утверждения, он может представлять собой целую концепцию, теорию. В связи с этим возможны и опровержения отдельных ее частей. И сложные аргументативные процессы разбиваются на части такого именно типа.

В отличие от простых форм аргументации в спорах и дискуссиях существенную роль играет постоянный поиск аргументов, подтверждение и критика их, отбор приемлемых – при этом для обеих сторон. Указанные выше правила о том, что аргументы в процессе аргументации должны быть истинными и в той или иной мере обоснованными, здесь, по существу, играют роль лишь в том смысле, что указывают цель, к которой надо стремиться.

Будучи сложными процессами, споры могут делиться на виды по разным аспектам. Но из множества возможных оснований выделяют обычно два – цель ведения спора и манеру его ведения. Наиболее существенным основанием является первое из указанных. По цели выделяются споры для истины, для убеждения и для победы.

Целью спора для истины является обоснование истинности или ложности выдвигаемого тезиса, то есть выявление оснований для принятия или непринятия его. Такие споры называют научными, эпистемическими, логическими.

В спорах для убеждения какая-то из сторон стремится убедить другую или присутствующих при споре в приемлемости или неприемлемости обсуждаемого положения, а иногда и просто в том, что следует или не следует совершать те или иные поступки. Конечно, и в спорах для истины, выявляя основания для принятия или непринятия тезиса, мы тоже убеждаем оппонента в приемлемости или неприемлемости его. При этом, однако, имеем в виду убеждение особого рода, а именно рациональное (логическое) убеждение; к тому же это не задача научного спора или, по крайней мере, не основная его задача: в строгих науках доказывают часто даже то, в чем люди уже вполне убеждены, доказательство в таких случаях необходимо как условие систематичности знания. В спорах же для убеждения, убеждение – самоцель. Иногда даже сам убеждающий уверен в неистинности или сомневается в истинности того, в чем он убеждает другого, исходя из каких-то особых своих интересов. Здесь возможны и методы не рационального, не логического убеждения, когда, наоборот, даже сознательно нарушаются логические правила аргументации; помимо логического широко применяется эмоционально-психологическое воздействие вплоть до гипнотического влияния.

Известный русский адвокат Ф.Н. Плевако, часто не отрицая виновности подсудимого, только благодаря своему вдохновению, остроумию, красноречию и умению глубоко проникать в психологию людей, склонял присяжных заседателей к оправданию подсудимых. Так, чтобы добиться оправдания своего подзащитного – священника, судимого за серьезное преступление, которое обычно сурово наказывается,– Ф.Н. Плевако достаточно оказалось одной, по существу, фразы: «Господа присяжные заседатели! Много лет этот человек отпускал нам наши многочисленные грехи... Так неужели мы не отпустим ему один раз его грех?!»

Когда судили полунищую старуху, укравшую у соседей грошовый чайник, прокурор, зная приемы Ф.Н. Плевако, которыми он пользуется, чтобы разжалобить присяжных, и решив предупредить его в этом, расписал в своей речи насколько она выглядит жалко, что она вызывает не гнев, а сострадание... Но, заключил он, она все-таки заслуживает обвинительного вердикта, поскольку посягнула на святая святых – на частную собственность, которая составляет экономическую основу нашего общества... Государство рухнет, если мы решительно не будем пресекать любые посягательства на его основы! На это Ф.Н. Плевако ответил в том духе, что Россия прошла сквозь многие испытания и лишения: набеги половцев, ужасы татаро-монгольского ига, нашествие Наполеона и т.д. Но устояла при этом и лишь крепчала все более и более... Но вот старуха украла чайник... и этого Россия, конечно, не выдержит! Ну и ясно, что женщина была оправдана.

Споры для победы – это своего рода интеллектуальное фехтование. В этом споре его участники вовсе не озабочены тем, истинны или ложны обсуждаемые ими положения, а также не стремятся убедить друг друга в том или ином. Цель состоит в том, чтобы во что бы то ни стало создать видимость доказанности или опровергнутости некоторого положения, лишив противника контраргументов, и таким образом одержать победу в интеллектуальном поединке.

Строго говоря, момент соревновательности, дух состязательности в той или иной мере имеет место в любом споре. Но в спорах описываемого вида к нему сводится все содержание обсуждения. К числу таких споров относятся, в частности, известные схоластические споры – споры чисто словесного характера. Эти споры часто называют эристическими. Широкое распространение споры такого рода имели место в Древней Греции и была особая категория людей – софистов,– которые специально практиковались в интеллектуальном фехтовании и демонстрировали свое искусство перед многочисленной публикой. Именно борьбе с софистами Аристотель посвятил свой трактат «О софистических опровержениях».

В спорах для убеждения возможны, а в спорах для победы обычно даже применяются так называемые уловки. Уловка – это прием, который сознательно применяется для того, чтобы затруднить ведение спора своему противнику или облегчить его ведение для себя. По существу, уловки – это некоторые нарушения принципов нормального научного спора. Поэтому в научном споре они просто неуместны в силу самих определений как уловок, так и научного спора.

Логику интересуют, собственно говоря, научные споры. Остальные, как объекты изучения, относятся, скорее, к сфере психологии, а логику интересуют лишь постольку, поскольку в них применяются нарушения логических требований аргументации и в качестве приемов ведения спора применяются логические уловки – сознательное нарушение тех или иных логических правил,– называемые софизмами; несознательное нарушение логических правил в споре, или вообще в некотором рассуждении, называется паралогизмами.

По манере, по способу ведения споров можно различать такие, где участники относятся с уважением друг к другу, не допускают никаких личных выпадов, оскорбительных эпитетов, оценок высказываемых мнений. С. Поварнин, автор специальной работы о спорах (Поварнин С.И. Спор. О теории и практике спора//Вопросы философии.– 1960.– № 3.), называет такие споры джентльменскими, противоположную этой форму ведения спора квалифицирует как хамскую. Само собой ясно, что представляет собой форма, противоположная джентльменской. Естественной формой ведения научного спора является, безусловно, первая. Вторая относится к спорам для победы и в меньшей мере для убеждения.

 

Научный спор как форма познавательной деятельности. Эпистемически-эвристическое и социально-педагогическое значение научных споров

В подлинно научном споре и пропонент, и оппонент в качестве основной цели имеют выяснение истинности или ложности самого обсуждаемого тезиса. Это выражается в том, что каждый из них не только не препятствует и не мешает деятельности другого, но, наоборот, при каждой возможности стремится способствовать его успеху. Пропонент, например, внимательно относясь к контраргументам, которые выдвигает оппонент, естественно должен стремиться к выяснению, уточнению и даже, по возможности, к добавлению их, хотя основная его задача состоит в опровержении этих контраргументов. В свою очередь, оппонент никак не препятствует этим опровержениям и готов даже содействовать им. Такое соединение усилий, направленных на всестороннее рассмотрение вопроса, на поиск всех возможных аргументов как за, так и против обсуждаемого тезиса, делает эту форму обсуждения весьма эффективным приемом научного познания.

Научный спор, дискуссия (Термин «дискуссия» употребляют иногда как синоним спора или как разновидность спора. Однако часто предметом дискуссии является не обсуждение некоторого готового тезиса, а обсуждение того или иного вопроса, коллективный поиск решения некоторого выдвинутого вопроса. Хотя при этом могут, и обычно складываются различные мнения и тем более если они сложились уже заранее по данному вопросу, то естественно возникает и обычный спор.) являются формами коллективного научного поиска. В процессе их подготавливается научный материал, из которого часто рождается ИСТИНА. Однако значение спора состоит не только в том, чтобы найти истину, но и в том также, что сама эта деятельность является чрезвычайно полезной для развития интеллектуальных способностей участвующих в ней людей. Наряду с тем, что при этом развиваются интеллектуальная интуиция, творческие способности, эта деятельность позволяет оттачивать известные приемы логического мышления, вырабатывает автоматизм их применения. Если физические упражнения направлены на развитие тела, то научные споры – это интеллектуальные упражнения, направленные на развитие того, что составляет прежде всего сущность человека – его интеллект, мыслительные способности.

Не случайно, что многие народы во времена их расцвета увлекались интеллектуальными турнирами, если не в большей мере, то так же, как и спортивными. В этом, очевидно, проявлялся инстинкт нации, подсказывающий ей, что развитие интеллекта – это гарантия и необходимое условие ее будущего развития и успехов. В Древней Греции, например, это было важным элементом подготовки аристократической молодежи к будущей судебной и общественно-политической деятельности.

И очевидно, что в гораздо большей степени это все должно бы относиться к нашему настоящему, когда широко осознано, что решающую роль в современной жизни играет именно интеллектуальная деятельность людей, что именно научное знание составляет основу не только всего современного производства, но и всей социальной жизни вообще. Не следует ли из всего этого, что споры должны быть одной из важных форм педагогического процесса? Что именно эта форма прежде всего способствует развитию творческих способностей мышления и именно она обеспечивает формирование культуры мышления? Знаменательно, что даже при отсутствии специальной организации этой формы деятельности в школе научные споры стихийно возникают между учащимися. Не есть ли это интуитивное стремление к коллективной интеллектуальной деятельности, к развитию интеллектуальных способностей?

Каким образом спор, дискуссию следует внедрять в педагогический процесс – это, конечно, не простой вопрос. Однако нет сомнения, что нужны поиски его решения. Очевидно, что какие-то уроки, например, литературы, истории могут быть организованы так, что преподаватель выступает в качестве организатора спора, выдвигает тезис, выделяет спорные моменты и дает возможность учащимся хотя бы в какой-то мере выступить с попытками доказательства, опровержения или уточнения тезиса. Конечно, полезен был бы последующий разбор состоявшейся дискуссии, в частности, и с точки зрения логики аргументации, ее убедительности и корректности. Полезна, очевидно, и уже известная практика организации «ролевых дискуссий» с предварительным распределением тем выступлений и определением их авторов. Так или иначе указанная задача должна решаться. Она, безусловно, составляет часть общей проблемы перестройки образования в нашей стране.

Итак, споры, о которых сейчас идет речь,– это научные споры. «Научные» – здесь не в том смысле, что обсуждаются тезисы какой-то науки. Это могут быть и утверждения повседневной жизни. Научным является сам способ ведения спора, соответствующий его цели, каковой является достижение истины – это понимание спора с точки зрения логики. И здесь она, как и обычно, акцентирует внимание не на том, что имеет место в действительных процессах мышления, а на том, как должно осуществляться мышление с точки зрения критериев логической правильности и рациональности вообще. Но в действительности споров, в описанной выше идеальной форме, обычно, к сожалению, не бывает и нередко спор, по изначальному замыслу научный, превращается в конце концов в шумные перебранки, в которых участники даже перестают слушать друг друга, не говоря уже о том, чтобы вникать в смысл того, что кто-то из них пытается высказать. Такой «спор» превращается в некоторую свару, которую Аристотель называл логомахией, в ней участники спора пытаются навязывать свои решения отнюдь уже не научными, логическими способами, а обсуждение вопросов сводится к «обмену ударами» и часто ниже пояса...

Что является причиной того, что во многих случаях не выдерживается естественный для научных споров способ их ведения? Прежде всего такой причиной может быть отсутствие логической культуры у участников спора. Далее, играют роль обычные человеческие недостатки и слабости, связанные к тому же с определенными социальными обстоятельствами. Так, например, в силу обостренного честолюбия и самолюбия человек не может поступиться тем, что ему дорого – особенно собственными научными результатами и привычками. В таком случае он не только не воспринимает выдвигаемые против его тезиса возражения, но может даже явно игнорировать их, закрывая глаза на факты, опровергающие защищаемый им тезис. Или, наоборот, человек, в силу его какого-то особого положения в обществе или зависти, ревнивого отношения к успехам другого, неприязненно, а иногда даже с раздражением, относится к выдвигаемому тезису, в силу чего лишается способности объективно оценивать доводы, поддерживающие тезис, и говорящие за него факты.

Весьма отрицательную роль в научных дискуссиях играет догматизм, косность человеческой мысли, приверженность к устоявшимся взглядам, в силу которых человек не может найти в себе силы объективно оценивать действительное положение дел. С большим трудом, например, представители науки могут отказываться от устоявшихся, привычных теорий. Существует даже афоризм, что новое в науке завоевывает господствующее место тогда лишь, когда «вымирают» представители старых взглядов.

Известно немало случаев, когда люди – в силу тех или иных социальных условий – не находят в себе мужества выступить против даже таких положений, неправильность которых для них является совершенно ясной (в подобных случаях выручает иногда лишь наивность и непосредственность какого-либо «мальчика», позволяющая ему заявить, что «король-то голый»).

Ясно, что, несмотря на естественность указанных факторов, они не являются абсолютно непреодолимыми и каждый порядочный и научно-добросовестный человек может в конце концов найти в себе силы для их преодоления ради той высокой цели, которая называется ИСТИНОЙ и ради которой многие люди шли и на костры, и на плахи.

Нельзя упускать из вида и того, что всегда, к сожалению, находятся люди, которые как раз не заинтересованы в правильных решениях вопросов и с готовностью используют человеческие слабости для достижения своих корыстных целей. В спорах такие именно люди и используют уловки, отнюдь не только логического характера.

 

Уловки споров и способы их нейтрализации

Среди уловок споров – возможных сознательных отступлений от нормальных принципов научно-рационального ведения спора – с одной стороны, выделяют уловки логического характера, с другой – уловки социально-психологического и организационно-процедурного характера.

Уловки логического характера называют софизмами. Это,– как мы уже говорили, сознательное нарушение тех или иных правил логики, применение заведомо неправильных способов рассуждений, маскируемых под правильные.

Множество возможных софизмов едва ли можно перечислить, в этом, впрочем, нет и необходимости, поскольку каждому правилу и принципу логики может соответствовать возможное его софистическое извращение. Однако в истории логики зафиксированы некоторые особые, хитроумные способы введения людей в заблуждение или, по крайней мере, формирующие логические головоломки.

Среди древних греков были люди, которые специализировались на софизмах ради потешения публики. Это интеллектуальные фокусники, которые брались доказать или опровергнуть все, что угодно. Софист мог взяться доказать, например, что твой отец – пес, мало того, что и сам ты – пес.

– У тебя есть пес? – спрашивает он.

– Да, есть.

– И от него есть щенки у соседней собаки? – продолжает софист.

– Да, это я видел сам, щенята от него.

– Значит он отец. И он твой. Следовательно, он твой отец!

Человеку доказывают, что у него есть рога: «То, что ты не потерял, у тебя есть. Рогов ты не терял, значит они у тебя есть!»

Человеку ставят вопрос, естественно, как будто, требуя ответа «Да» или «Нет» (вспомните ли-вопросы): «Перестал ли ты бить своего отца?» Но при любом из этих ответов, отвечающий оказывается в нелепом положении.

Нейтрализация софизмов может, в частности, состоять в раскрытии содержащихся в них логических ошибок. Ясно, что в первом случае имеется явная подмена понятий: «Твой пес, являющийся отцом щенков» и «твой отец». Во втором случае – явно ложный аргумент («аргумент, доказывающий слишком много»). В третьем – неправильно поставленный вопрос: вопрос с ложной предпосылкой о том, что ты бил своего отца. Другой не менее эффективный способ нейтрализации софизмов – использование «опровергающей аналогии рассуждения»:

— Перестал ли я бить своего отца? Хорошо, я отвечу на Ваш вопрос, но прежде Вы ответьте столь же четко, перестали ли Вы страдать энурезом?

Подобных софизмов дошло до нас большое количество, хотя под названием софизмов иногда имеются в виду фактически антиномии – логически парадоксальные ситуации, содержащие в рассуждении какие-то дефекты, для которых в логике не найдено общепринятого решения. Например, софизм «Куча»: «Последовательным добавлением песчинок нельзя составить никакую кучу. Если Вы взяли одну песчинку, то это явно не куча, две песчинки тоже не куча. И никогда из не-кучи нельзя получить кучу, добавляя одну песчинку».

Трудность здесь состоит в характере самого свойства «куча» (которое принадлежит к классу свойств, называемых не индуктивными). Особенность его состоит в том, что нет определенного промежутка, когда нечто становится или перестает быть кучей.

Софизм «Эватл и Протагор»: Протагор учил логике молодых людей, готовящихся к занятиям адвокатско-судебной деятельностью. Эватл брал у него уроки, обязуясь – по договору – заплатить ему лишь в том случае, когда он выиграет свой первый процесс (что будет свидетельствовать о хорошем качестве его подготовки). Закончив курс обучения, Эватл не ведет процессов. Протагор, чувствуя, что таким способом Эватл хочет уклониться от оплаты, заявляет ему: «Напрасно ты надеешься, что можешь не уплатить мне, не ведя процессов. Я подам на тебя в суд. И ты уплатишь мне либо по приговору суда, либо – если приговор будет в твою пользу – согласно нашему договору, ибо это будет означать, что ты выиграл свой первый процесс». Эватл отвечает ему на это: «Хоть ты, учитель, и мудрый человек, но рассуждения твои несостоятельны. Если ты подашь в суд, то я ни в каком случае не уплачу: если приговор будет в твою пользу, то это будет означать, что я проиграл свой первый процесс, и не буду платить согласно нашему договору; если же суд укажет мне не платить, я не уплачу согласно приговору суда!»

Заметим, что причина возникшего здесь недоразумения состоит в промахе, который допустил Протагор при заключении договора: говоря современным логическим языком, он не учел, что предикаты «выиграешь» или «не выиграешь» могут относиться только к людям, ведущим процессы, и не предусмотрел в договоре пункт, чтобы Эватл оказался в числе этих людей.

УЛОВКИ СОЦИАЛЬНО-ПСИХОЛОГИЧЕСКОГО ХАРАКТЕРА

Основную группу здесь составляют уловки, которые касаются не содержания обсуждаемых положений, а прежде всего личностей тех, кто выдвигает эти положения или опровергает их.

«Приманка». Желая склонить оппонента к принятию тезиса, подкупают его лестью, утверждая, например, что он, как человек проницательный, эрудированный, интеллектуально развитый, должен согласиться с тезисом. Честолюбивого человека ставят тем самым перед дилеммой: либо принять тезис, либо подорвать хорошее мнение о себе.

«Принижение». Стремясь оправдать неприятие тезиса, оппонент подчеркивает такие, например, отрицательные черты того, кто выдвигает это положение, как необразованность, неосведомленность в данной области или то, что он уже проявил себя как человек, когда-то неправильно решивший какой-то вопрос и т.п. Цель такого рода усилий – породить сомнение в истинности тезиса.

«Самовосхваление». «Я такой-то и такой-то (дается высокая оценка себя по всем параметрам)». А ты, дескать, в противоположность мне, все, что осталось. Уловка состоит в том, что прямо не говорят «кто ты», но по тому «кто я» и «с кем ты споришь» – нетрудно догадаться.

«Проницательность» (или «Чтение в сердцах»). Эта уловка состоит в том, что непринятие соперником тезиса стараются оправдать, усматривая какие-то особые мотивы, которые мешают тому, чтобы тезис был принят, рассуждая, например так: «Всем здесь ясно, что Вы давно бы согласились со мной, но должность (или мундир, или партийная принадлежность и т.п.) не позволяют Вам это сделать».

«К здравому смыслу». Используется как апелляция к обыденному сознанию в ситуациях, когда требуются специальные знания, выходящие за рамки бытовых. Уловка имеет эффект у людей, склонных переоценивать «жизненный», «практический» опыт и доверяться здравому смыслу и интуиции.

«К выгоде». Смысл уловки состоит в том, что вместо логического обоснования истинности тезиса агитируют за рассмотрение его как истинного в силу его выгодности в моральном, политическом, экономическом или каком-либо другом отношении.

«К верности». Вместо доказательства тезиса склоняют к его принятию в силу верности традициям, партийным убеждениям или даже личной преданности человеку, выдвигающему тезис. Когда речь идет о явлениях общественной жизни, нередки апелляции к мнению народа, претензии говорить «от имени народа».

«Досказывание». «Позвольте я доскажу вашу мысль...». «Понятно, куда вы клоните, что хотите доказать...». «Нетрудно предугадать продолжение вашей мысли...».

Подобные выражения свидетельствуют о попытках сделать логические выводы из какой-либо имеющейся информации. Такие выводы, действительно, можно делать, иногда они сами напрашиваются. Уловка же состоит в таком домысливании («досказывании») утверждений соперника, когда осуществляется неправомерное, выходящее за рамки известных фактов мысленное развитие реальной ситуации.

Очень часто эта уловка встречается и в другой модификации: «А завтра...», пользующейся успехом в аудиториях с недостаточной степенью организованности мышления. «Сегодня от нас требуют этого. Завтра потребуют другого! А послезавтра... До каких же пор мы будем терпеть это глумление?!...».

«Ярлык». Однозначная, бездоказательная оценка утверждений соперника, не содержащая никаких доводов, с целью отнести тезис к категории чего-то, явно неприемлемого, и таким образом дискредитировать его: «Ваш тезис эквивалентен, утопичен, играет на руку» ... и т.п.

«Выбор терминологии». Уловка связана с выбором слов таким образом, чтобы сформировать у слушателей либо отрицательное, либо положительное отношение к обсуждаемому тезису или доводам. Ясна, очевидно, разница, которая возникает в зависимости от того, какие из слов выбираются для обозначения соответствующих явлений: попы – духовенство, шпион – разведчик, скотник – специалист по навозоудалению, аппаратчики – работники сферы управления и т.п.

«Демагогия». Явное преувеличение последствий принятия или непринятия тезиса, ложное, искаженное представление этих последствий, стремление сыграть на чувствах, вызвать даже низменные инстинкты людей и т.п.

«Философия». Широко известна способность многих людей говорить «мудреным языком». С помощью набора слов, лишенных ясного смысла, маскируется неясность высказанной мысли или даже отсутствие ее вообще. В процессе спора к такой уловке может прибегать оппонент, желая отвергнуть тезис, не имея против него аргументов по существу. Таким способом добиваются даже впечатления большой мудрости и глубокомыслия.

«Трескотня». Ошарашивание очень быстрым темпом речи и множеством мыслей, быстро сменяющих одна другую.

«Вдалбливание». Уловка состоит в постепенном приучивании оппонента и слушателей к какой-либо мысли, в защиту которой доводы не приводятся, но после неоднократного повторения, возможно в разных вариантах, она преподносится как очевидная или даже доказанная.

«Многозначительная недосказанность». Человек, выдвигающий тезис, чувствует недостаток аргументов в пользу него и делает глубокомысленный и многозначительный вид, что он мог бы, конечно, сказать еще и еще что-то в защиту тезиса, но не считает уже нужным это делать.

«Слабое звено». Из выдвинутого пропонентом тезиса и аргументов в его защиту выбирают наиболее уязвимый, опровергают его в резкой форме и преподносят дело таким образом, что остальные доводы даже внимания не заслуживают. Уловка имеет успех в том случае, если пропонент не возвращается к теме или лишен этой возможности.

«Мнимая невнимательность». Уловка состоит в том, что человек пропускает, как говорят, «мимо ушей», умышленно не замечая («забывая») те доводы противника, на которые он не может ответить по существу.

«Бремя доказательства». Выдвигая тезис, не приводят аргументов, из которых он следует, а предлагают оппоненту или даже требуют от него опровергнуть это положение («... а что, собственно, Вы имеете против?»). Ясно, что эта уловка ограничивает возможности для развернутой критики собственной позиции и перемещает центр спора. В том случае, если оппонент поддался этому и начинает критиковать выдвинутый тезис, приводя различные аргументы, то стараются вести спор вокруг этих аргументов, выискивая в них недостатки, не предоставив для обсуждения свое доказательство, превращая себя в оппонента, а действительного оппонента – в пропонента. Эта уловка реализует один из принципов эристического спора: «Возлагай бремя доказывания на противника. Разрушать рассуждения критикой легче, чем самому доказывать».

«Симуляция непонимания». Не зная, как возразить на те или иные доводы противника, человек старается представить дело так, что он не понимает слов или вообще того, что ему говорят и посредством множества надуманных вопросов либо уходит от обсуждения, либо даже создает впечатление несостоятельности утверждений соперника.

«Механические уловки». Использование отвлекающих жестов, физического воздействия на оппонента.

 

УЛОВКИ ОРГАНИЗАЦИОННО-ПРОЦЕДУРНОГО ХАРАКТЕРА

Одна из них, например,– «брать горлом». Не желая воспринять тезис или слушать возражения противника, человек повышает тон, начинает его перебивать, не дает ему высказать свою мысль, словесно забивает его в конце концов, вообще лишая возможности продолжать обсуждение.

Многие организационно-процедурные уловки относятся к публичным аргументативным процессам, в частности, к дискуссиям, на которых предполагается выработать решение по тем или иным вопросам. Они могут состоять в использовании следующих приемов.

Материалы, нужные для обсуждения, не раздаются вовремя или раздаются выборочно.

Слово предоставляется сначала тем, чье мнение импонирует и известно, таким образом программируется первичная установка.

Обсуждение приостанавливается на выступающем, позиция которого более соответствует заранее намеченной цели, то есть используется известная особенность человеческой психики – тверже запоминаются первое и последнее выступления, они сильнее влияют на психологическую установку.

Одних выступающих жестко ограничивают в соблюдении регламента, другим позволяют выйти из регламента. То же самое в характере высказывании: одним «прощают» резкости в адрес оппонентов, другим делают замечания.

Сначала «выпускается пар» на малозначительных и несущественных вопросах, а затем, когда все устали или находятся под впечатлением предыдущего обсуждения, выносится вопрос, решение которого хотят получить без обстоятельного обсуждения.

Принятые решения фиксируются жестко, не допускается возвращение к ним даже при поступлении новых данных, заслуживающих внимания и важных для выработки окончательного решения.

Если намечается решение, нежелательное для кого-либо из участников дискуссии, он предлагает отложить решение вопроса, выдвигая специально придуманные для этого причины.

Бывает и так, что принятие решения предлагается отложить, потому что спор зашел в тупик, слишком разгорелись страсти и видно, что удовлетворительным образом вопрос не может быть решен. Но это уже не уловка, а, скорее, определенная тактика ведения дискуссии.

Для того, чтобы не попадаться на уловки и не стать объектом манипуляции недобросовестного оппонента, прежде всего, конечно, необходимо уметь распознавать уловки. Дальнейшие действия могут строиться как в зависимости от характера спора, так и в зависимости от природы самой уловки, подсказывающей, как ее нейтрализовать. Ввиду многообразия уловок, трудно говорить о всех возможных способах их нейтрализации, но главным из них является разоблачение уловки. Если это сделано квалифицированно, с достаточным анализом существа и предназначения уловки, то это отбивает у данного и у других участников спора охоту прибегать к ним, поскольку у каждого участника спора возникает уверенность, что в данном споре надо работать честным образом и нельзя возлагать надежды на успех незаконных приемов.

Иногда уловки делят на допустимые и недопустимые. Вернее было бы сказать, что все уловки не допустимы, поскольку они являются нарушением определенных норм ведения спора. «Допустимые уловки» это, скорее, тактические приемы ведения дискуссии.

 

Рационализация споров: понятие о стратегии и тактике спора

Поскольку дискуссия представляет собой определенную борьбу, иногда ее и характеризуют как «сражение» (Она подобна, например, футбольному сражению с той, конечно, разницей, что во втором главным средством являются ноги и в меньшей степени голова, тогда как в первом все решает голова.), то правомерно говорить здесь о стратегии и тактике дискуссии.

Стратегия спора – это план его ведения. Однако она может и не быть единой для всех сторон, чаще всего оппоненты и пропоненты могут иметь каждый свою особую стратегию. Поскольку в споре (как и на футбольном матче) все очень изменчиво и подвижно, постоянно изменяются направления атак, складываются ситуации, которые невозможно предугадать заранее, то нельзя говорить о более или менее единой и неизменной стратегии спора, хотя не исключается все-таки возможность наметить некоторые основные ее контуры.

Так, тот, кто выступает с защитой некоторого тезиса, естественно, продумывает возможные доводы, а также последовательность их выдвижения, чтобы обеспечить максимально возможную степень обоснованности тезиса. При этом аргументы могут делиться на основные и резервные. Основные – те, которые представляются достаточными для обоснования тезиса; резервные – на случай неожиданных осложнений. Естественно, конечно, продумываются и возможные контраргументы и подходящие ответы на них.

Оппоненты, знающие заранее содержание тезиса, продумывают его уязвимые места и возможные опровергающие доводы.

При организации дискуссии для обсуждения некоторого вопроса заранее учитывается круг лиц, уже работавших над ним, намечается круг выступающих, от которых можно ожидать наиболее плодотворных идей по обсуждаемому вопросу. Если заранее известны различные точки зрения по данному вопросу, то естественно выбрать круг людей, которые могли бы обеспечить наиболее содержательный спор.

Составление плана дискуссии, то есть выработка стратегии ее ведения, в сочетании с определенными условиями организационного характера (Ясно, что если дискуссия массовая, то, по крайней мере, кем-то должно быть обеспечено ее нормальное ведение по форме.), является важнейшим условием рационализации спора.

Эффективность спора в значительной мере зависит часто и от тактики его ведения. Вопросы о тактике, как и стратегии спора, не являются еще разработанными, но, безусловно, заслуживают серьезного внимания.

Тактические приемы разнообразны и характер их в значительной мере зависит как от состава аудитории, от интеллектуальных и психических особенностей спорящих, так и от содержания спора. Мы остановимся здесь на наиболее важных моментах.

Прежде всего поговорим о поведении людей и манере держать себя в споре. Если речь идет о теоретическом споре, то от участника такого спора необходимо прежде всего спокойствие и уравновешенность, способность не поддаваться естественно возникающим волнениям, эмоциям, особенно когда не удается обоснование тезиса и намечаются серьезные признаки его опровержения. Если в споре разгораются страсти, происходит всплеск эмоций, то достаточно, чтобы нашелся кто-то, кто, спокойно реагируя на возбужденные выпады, на проявление раздражения противника, в ответ демонстрирует спокойный разбор его аргументов и собственной выдержкой гасит волны возбуждения.

Весьма успокаивающе и миротворчески действует на эмоционального и раздраженного оппонента или, наоборот, на вышедшего из равновесия пропонента внимательное и доброжелательное отношение к тому, что высказывает противник. Магическое действие оказывают в таких случаях выражения: «Ваша мысль очень интересна, над ней следует хорошо подумать», «Это очень остроумное замечание, я не предвидел этого» и т.п.

Ну и конечно, от каждого участника спора требуется открытость для убедительных аргументов. Для того чтобы уметь переубеждать других, надо и самому быть открытым для восприятия убедительных доводов оппонентов.

Вместо прямого опровержения аргумента, который приводит возбужденный противник, полезно использовать прием условного принятия его доводов с тем, чтобы шаг за шагом путем выведения из них сомнительных следствий подвести его к нужному окончательному выводу, обратив его таким образом в соучастника опровергающего рассуждения.

Этот же прием условного принятия положений, кажущихся ложными, за истину может быть полезен на определенном этапе дискуссии и с логической точки зрения. Особенно, когда не видно способов прямого их опровержения: «Предположим, Ваши замечания истинны, давайте попробуем обсудить, что из них следует...» И тогда совместно с оппонентом возможно найдутся косвенные опровержения каких-то положений.

Когда противник выдвигает контрдовод против Вашего тезиса, то прежде чем решать вопрос, является ли он истинным или ложным, полезно посмотреть, действительно ли он сам или следствия из него хотя бы частично опровергают тезис. Часто оказывается так, что контрдовод просто совместим с Вашим тезисом. Если установлено последнее, то нет уже надобности вообще обсуждать его с точки зрения истинности или ложности.

На каждом этапе дискуссии очень важно всегда иметь представление о ней в целом; сосредоточивая внимание на обсуждении каких-то положений, необходимо «боковым зрением» охватывать и все «поле сражения» в целом: учитывать, какие доводы приняты, отвергнуты, какие еще остаются возражения против тезиса, подлежащие анализу.

Существенно не спешить использовать сразу все свои доводы в защиту тезиса. Полезно, приводя их последовательно выявлять при этом и возникающие возражения, что в свою очередь, помогает оценивать состоятельность или несостоятельность других имеющихся в запасе доводов. Изложив же сразу все имеющиеся у Вас аргументы. Вы рискуете оказаться перед фактом, что многие из них будут опровергнуты и, не имея ничего другого в запасе, Вам ничего не останется, как признать свое поражение или, по крайней мере, отложить спор до лучших времен.

 

Упражнения

 

1. Проанализируйте следующие доказательства – выявите тезис, имеющиеся или подразумеваемые аргументы, оцените аргументы с точки зрения их обоснованности и связи с тезисом, следует ли он из аргументов:

а) О том, что Николаев болен, свидетельствует повышенная температура. Известно, что у здоровых людей температура колеблется от 36 до 37 градусов. У Николаева 38,5. Следовательно, Николаев не может считаться здоровым. Более того, у Николаева плохое самочувствие, которое испытывают все больные люди. Это также свидетельствует о том, что Николаев болен.

б) Если бы Петров совершил убийство, то он был бы на месте преступления в ту ночь, когда оно было совершено. Но в ту ночь Петров не был на месте преступления, что подтверждено свидетельскими показаниями. Следовательно, Петров не совершал данного убийства.

в) Поскольку риск, как говорится, благородное дело, и очевидно, что дача взятки должностному лицу, безусловно, представляет собой риск, отсюда с необходимостью по правилам логики следует, что дача взятки должностному лицу является делом благородным.

г) Логика тесно связана с грамматикой. В самом деле, не существует мыслей вне языковой оболочки. Для того чтобы сообщить другому свою мысль, мы должны выразить ее в языковой форме. И наоборот, всякое слово, всякая фраза выражает какую-то мысль. Все это доказывает тесную связь логики с грамматикой.

д) Снег не может лежать на высоких горах, так как чем ближе к солнцу, тем теплее, и притом снег всегда тает раньше на высоких местах, хотя в лощинах еще держится.

е) Евгений Онегин был человеком исключительной порядочности и благородства. Это видно хотя бы из того, что, не чувствуя в своей душе любви к Татьяне, он чистосердечно ей в этом признался.

ж) Один критик высказал суждение о какой-то книге, прочитав всего-навсего одну страницу этой книги. Когда это ему поставили в упрек, то он ответил: «Если я желаю определить вкус вина в бочке, неужели для этого я должен выпить всю бочку? Одной рюмки вполне достаточно, чтобы произвести оценку».

2. Как бы Вы могли опровергнуть следующую аргументацию? Философ Диоген из Аполлонии считал, что разум человека обусловлен вертикальным положением тела человека, благодаря чему человек вдыхает более чистый воздух, тогда как животные с головою, наклоненной к земле, вдыхают воздух, загрязненный влагой земли. Точно так же и дети, вследствие своего малого роста, менее умны, чем взрослые.

3. Определите, правильны ли следующие рассуждения с точки зрения критериев теории доказательств:

а) Иванов говорит, что аргументация – это чисто психологический процесс. Но говорить так, значит, высказывать ложное суждение, следовательно, Иванов высказывает именно такое суждение. А высказывать ложное суждение, значит, говорить ложь. Но тот, кто говорит ложь – лжец! А лжец достоин презрения. Следовательно, Иванов достоин презрения.

б) Во время бунта плебеев в древнем Риме сенатор Менений Агриппа умиротворял их таким образом. «Каждый из вас,– говорил он,– знает, что в организме человека существуют разные части, причем каждая из них выполняет свою определенную роль: ноги переносят человека, голова думает, руки работают. Государство – это тоже организм, в котором каждая часть предназначена для выполнения своей роли: патриции – это мозг государства, плебеи – это его руки. Что было бы с человеческим организмом, если бы отдельные части его взбунтовались и отказались выполнять предназначенную для них роль? Если бы руки отказались работать, голова – думать, тогда человек был бы обречен на гибель. То же самое случится и с государством, если его граждане, подобно вам, будут отказываться выполнять то, что является их естественной обязанностью. А посему, заботясь о вас, неразумные, призываю прекратить бунт!»

в) «Уважаемые коллеги! У меня, как и у всех, очевидно, присутствующих, нет ни тени сомнения в научной некомпетентности товарища Иванова. В самом деле, на протяжении всей, навязанной нам товарищем Ивановым дискуссии, он упорно отстаивает ложный, абсурдный, если хотите, тезис. Да, да! Именно абсурдный! И чтобы не уподобляться товарищу Иванову, я буду доказателен в подтверждении этого и без того, впрочем, ясного обстоятельства. Но тем не менее. Во-первых, аргументы, на которых строится доказательство товарища Иванова, ложны, поскольку описываемых событий не было, и это со всей убедительностью показал предыдущий оратор, да и сам Иванов перед лицом неопровержимых фактов теперь уже это признает. Но более того, и это во-вторых, рассуждение, с помощью которого товарищ Иванов пытался связать свои ложные аргументы с не менее ложным в силу этого тезисом, содержит, как все, наверное, заметили, грубейшую, непростительную логическую ошибку, о которой, товарищ Иванов, Вы прочтете в любом школьном учебнике логики. Я уверен, уважаемые коллеги, что сказанного вполне достаточно, чтобы сделать соответствующие выводы».

 

УДК 16

ББК 87.4я73

В 65

 

Войшвилло Е.К.

Логика: учеб. для студ. вузов/Е.К. Войшвилло, М.Г. Дегтярев.– М.: Гуманитар, изд. центр ВЛАДОС, 2010.– 527 с.– (Учебник для вузов).

ISBN 978-5-691-01688-2

Рассматривается круг логических вопросов и проблем, который можно охарактеризовать как «практическая логика». Анализируются вопросы практического применения логики, в частности, в педагогическом процессе. Особое значение имеет глава, посвященная логико-эпистемологическим и социально-психологическим аспектам аргументации (доказательство и опровержение, критика, споры и дискуссии и т. д.)

В учебнике удачно сочетается традиционная тематика с современным уровнем логико-методологических исследований.

Для студентов вузов.

 

© Войшвилло Е.К., Дегтярев М.Г., 2001

© ООО «Издательство ВЛАДОС-ПРЕСС», 2001

© ООО «Гуманитарный издательский центр ВЛАДОС», 2008

© Оформление. ООО «Гуманитарный издательский центр ВЛАДОС», 2008

Учебное издание

 

Войшвилло Евгений Казимирович

Дегтярев Михаил Григорьевич

 

ЛОГИКА

 

Учебник для студентов высших учебных заведений

 

Редактор И.Б. Нилова

Художник Ю.В. Токарев

Компьютерная верстка Ю.В. Одинцова

Корректор И.Б. Нилова

 

Лицензия ИД № 03185 от 10.11.2000.

Санитарно-эпидемиологическое заключение

№ 77.99.60.953.Д.010192.08.09 от 28.08.2009 г.

 

Подписано в печать 10.10.00.

Формат 60 x 90/16. Печать офсетная. Бумага газетная. Усл. печ. л. 33.

Тираж 10 000 экз. (1-й завод 1-3 000 экз.). Заказ № 5863.

 

Гуманитарный издательский центр ВЛАДОС.

119571, Москва, просп. Вернадского, 88,

Московский педагогический государственный университет.

Тел. 437-11-11, 437-25-52, 437-99-98; тел./факс 735-66-25.

E-mail: vlados@dol.ru

http://www.vlados.ru

 

ООО «Полиграфист».

160001, Россия, г. Вологда, ул. Челюскинцев, 3.

 

 

Скачано с www.znanio.ru

 

Скачано с www.znanio.ru