
|
Ұзақ мерзімді жоспардың бөлімі: Тригонометрия |
Мектеп: |
||||||
|
Күні: |
Мұғалімнің аты-жөні: |
||||||
|
Сынып: 9 |
Қатысқандар саны: |
Қатыспағандар: |
|||||
|
Сабақ тақырыбы |
Тригонометриялық функциялар және олардың қасиеттері |
||||||
|
Cабақтың түрі |
Жаңа тақырыпты оқып үйрену |
||||||
|
Осы сабақта қол жеткізілетін оқу мақсаттары (оқу бағдарламасына сілтеме) |
9.2.4.6 бірлік шеңбердің көмегімен тригонометриялық функциялардың жұптылығын (тақтылығын), периодтылығын , бірсарындылығын және таңбатұрақтылық аралықтарын түсіндіру; |
||||||
|
Сабақ мақсаттары |
Оқушылар: · бірлік шеңбердің көмегімен тригонометриялық функциялардың жұптылығын (тақтылығын), периодтылығын ,бірсарындылығын және таңбатұрақтылық аралықтарын түсінеді; |
||||||
|
Бағалау критерийлері |
Оқушы: · бірлік шеңбердің көмегімен тригонометриялық функциялардың жұптылығын (тақтылығын) анықтай алады; · бірлік шеңбердің көмегімен тригонометриялық функциялардың периодтылығын , бірсарындылығын және таңбатұрақтылық аралықтарын анықтай алады; |
||||||
|
Тілдік мақсаттар |
Оқушылар: бірлік шеңбердің көмегімен тригонометриялық функциялардың қасиетін сипаттайды; Пәнге қатысты лексика мен терминология: бірлік шеңбер, тригонометриялық дөңгелек, тригонометриялық функция, функцияның тақтығы/жұптығы, период, бірсарындылылық, таңбатұрақтылық аралықтары Диалогқа/жазылымға қажетті тіркестер: 1,2,3,4 ширекте синус/косинус/тангенс/котангенс таңбасы ... болады Функцияның периоды ...-ға тең болады. Функцияның өсу /кему аралығы ... Функцияның бірсарындылық аралығы ... |
||||||
|
Құндылықтарды дарыту
|
Құндылықтарды дарыту берілген сабақта жоспарланған іс-әрекеттер арқылы жүзеге асады. Оқуға, жағдайды талдауға, жаңа шарттарға бейімделуге, мәселе қоюға және шешім қабылдауға, топта жұмыс істеуге, өзінің жұмысының сапасына жауап беруге, өзінің уақытын ұйымдастыруға дағдылану. |
||||||
|
Пәнаралық байланыстар |
Физика,биология |
||||||
|
Бастапқы білім
|
«Функция», «аргумент» ұғымдарын біледі. Функцияның графигін және оның қасиетін біледі. Геометрия курсынан сүйір бұрыштың тригонометриялық функцияларының анықтамаларын біледі. |
||||||
|
Сабақ барысы |
|||||||
|
Сабақтың жоспарланған кезеңдері |
Сабақтағы жоспарланған іс-әрекет
|
Ресурстар |
|||||
|
Сабақтың басы
|
1. Ұйымдастыру кезеңі Мұғалім оқушылардың психологиялық мобильдігіне ықпал етеді, оқушыларды диалогке даярлығын орнатады. 2. Мәселе қою кезеңі. 1) Бірлік шеңберде синус дегеніміз не? 2) Косинус дегеніміз не? 3) Бірлік шеңберде тангенс дегеніміз не? 4) Бірлік шеңберді пайдаланып, кестені толтыру 3. Мақсат қою. Мұғалім сабақтың тақырыбы мен оқу мақсатын айтады. Оқушылармен бірге сабақ мақсаттары жасалады. Әрі қарай, мұғалім бағалау критерийлерін айтады, оқушылардың «жақын даму аймағы», сабақтың күтілетін нәтижелері айқындалады. |
үлестірмелер
|
|||||
|
Сабақ ортасы
|
Жаңа тақырыпты оқып үйрену. Ұжыммен бірге талдау Анықтама:
Синус (латынша
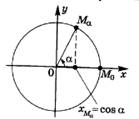
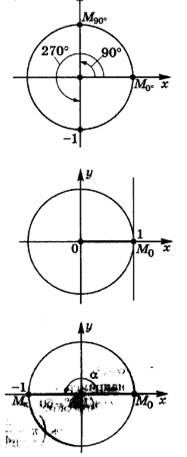
sіnus — дөңестік, иілу). y=sin Сұрақ: 1) ордината қай ширектерде оң болады? 2) ордината қай ширектерде теріс болады? Осыдан синус функциясының I және II координаталық ширектерде таңбасының оң, ал III және IV координаталық ширектерде теріс болатындығы анықталады.
1.
a) Егер
sin
яғни, егер sin
яғни, егер sin б,в
бөлімдерден sin Синус
функциясының периодтылығы үшін теңдік және синус
функциясының ең кіші оң периоды 2. а)
Бұл қасиет y(x) = sin(x) функциясының тақ екендігін бейнелейді, демек оның графигі бас нүктеге қарағанда центрлі-симметриялы орналасады.
б
Мысал: sin
в) sin
sin
г)
sin
sin
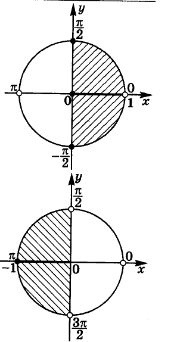
3. Синус функциясының таңба тұрақтылық аралықтарын анықтайық:
Бұл
теңсіздік
Бұл
теңсіздік
ü Функцияның анықталу облысы; ü Функцияның мәндерінің облысы; ü Жұп/тақтығы; ü Периодтылығы; ü Функцияның нөлдері; ü Таңбатұрақтылық аралықтары; ü Өсу, кему аралықтары; ü Максимум және минимум нүктелері. Бағалау дескрипторы: Функцияның анықталу облысы мен мәндерінің облысын анықтай алады Функцияның жұп-тақтылығы мен периодтылығын анықтай алады. Функцияның нөлдерінің анықтай алады Функцияның өсу, кему аралықтарын анықтай алады Функцияның максимум және минимум нүктелерін анықтай алады Топтық жұмыс Оқушыларды 3 топқа бөліп, 1- топқа косинус, 2 -топқа тангенс, 3 -топқа котангенс функциясын зерттеу ұсынылады. Оларға
Жұмыс аяқталған соң оқушылар өздерінің қорытындыларын көрсетеді және оларды интерактивті тақтадағы дайын жауаптармен салыстырады. Бағалау критерийлері: ü бірлік шеңбердің көмегімен тригонометриялық функциялардың жұптылығын (тақтылығын) анықтай алады; ü бірлік шеңбердің көмегімен тригонометриялық функциялардың периодтылығын,бірсарындылығын және таңбатұрақтылық аралықтарын анықтай алады;
Жауап тексеріліп болғаннан соң, жаңа топтар құрылып өзара оқыту үдерісі ұйымдастырылады.
Өткен материалды бекіту. Жұптық жұмыс. Оқушылар тригонометриялық функциялардың қасиеттерін бекіту мақсатында есептер шығарады. Тапсырманың дұрыс орындалуы мұғаліммен әрі жұбымен тексеріледі. Бағалау критерийлері: ü тригонометриялық функциялардың жұптылығын (тақтылығын) анықтай алады; ü тригонометриялық функциялардың периодтылығын , бірсарындылығын және таңбатұрақтылық аралықтарын анықтай алады;
|
Үлестірмелер
Бірлік шеңбер
|
|||||
|
Сабақтың соңы
|
4. Сабақты қорытындылау. Мұғалім сабақ мақсаттарына қайта оралады, олардың жету деңгейін талқылайды. Келесі сабақтарды жоспарлау үшін оқушыларға сұрақтар қойылады: - нені білдім, неге үйрендім; - не түсініксіз болып қалды; - не бойынша әлі де жұмыс істеу қажет. Сұрақтар ауызша немесе жазбаша талқылана алады. Сонымен қатар, оқушылардың эмоционалдық көңіл-күйін «Табысқа жету баспалдағы» арқылы бағалауға болады.
|
|
|||||
|
Саралау – оқушыларға қалай көбірек қолдау көрсетуді жоспарлайсыз? Қабілеті жоғары оқушыларға қандай міндет қоюды жоспарлап отырсыз? |
Бағалау – оқушылардың материалды меңгеру деңгейін қалай тексеруді жоспарлайсыз |
Денсаулық және
қауіпсіздік техникасының сақталуы |
|||||
|
Сабақта өзіне сенімсіз оқушылар біршама қабілетті оқушылармен бірге жұпта жұмыс жасайтындай етіп жасалған, сонда олар қабілетті оқушылармен жұмыс жасағанда көбірек біле алады. Қабілетті оқушылар өздерінің қабілеттерін консультант ретінде айқындай алады. Жұптағы немесе жеке жұмыстарда Сіз өзіне сенімсіз оқушыларға көмекші сұрақтар қою арқылы көмектесе аласыз.
|
Формативті бағалау сабақтың әр кезеңінде өткізіледі (өзін-өзі бағалау, мұғалімнің критерий бойынша бағалауы). Оқушылардың тапсырманы орындау барысындағы қатысуы және диалогқа қатысуын бағылау арқылы бағалау. Жұптағы, топтағы тапсырмаларды орындауға жауапты реакция және прогресс әр оқушының үлесін бағалауға және қателердің бар болуын анықтау үшін қарастырылады.
|
Іс-әрекеттердің ауысып отыруы ең үлкен нәтижеге қол жеткізу мақсатында оқушылардың күші мен зейінін дұрыс үлестіруге ықпалын тигізеді. |
|||||
Қосымша 1 Косинус
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.