Алгоритмизация

ТЕМА: Основы алгоритмизации и программирования. Этапы разработки программ. Алгоритмы. Понятие алгоритма. Формы записи алгоритмов. Базовые структуры алгоритмов. Данные. Понятие типа данных. Преобразование типов.

ТИП: лекция

ЗНАТЬ:
1. Понятие алгоритма

2. Свойства алгоритма

3. Способы записи алгоритмов и уметь приводить примеры способов записи алгоритмов
4. Три вида алгоритмов

5. Символы записи графического алгоритма

6. Правила записи графического алгоритма

Алгоритм – последовательность чётко определенных действий, выполнение которых ведёт к решению задачи. Алгоритм, записанный на языке машины, есть программа решения задачи.

Алгоритм – это совокупность действий, приводящих к достижению результата за конечное число шагов.

Первое определение не передает полноты смысла понятия алгоритм, т.к. действия не обязательно должны следовать друг за другом – они могут повторяться или содержать условие.

Свойства алгоритмов:

1.        Дискретность (от лат. discretus — разделенный, прерывистый) – это разбиение алгоритма на ряд отдельных законченных действий (шагов).

2.        Детерминированность (от лат. determinate — определенность, точность) - любое действие алгоритма должно быть строго и недвусмысленно определено в каждом случае.

3.        Конечность – каждое действие в отдельности и алгоритм в целом должны иметь возможность завершения.

4.        Массовость – один и тот же алгоритм можно использовать с разными исходными данными.

5.        Результативность – алгоритм должен приводить к достоверному решению.

Основная цель алгоритмизации – составление алгоритмов для ЭВМ с дальнейшим решением задачи на ЭВМ.

Примеры алгоритма:

1.                 Инструкция по эксплуатации оборудования.

2.                 Правила дорожного движения.

3.                 Порядок сборки изделия на предприятии.

Способы записи алгоритмов

1.        Словесная (запись на естественном языке);

2.        Псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);

3.        Графическая (изображения из графических символов – блок-схема);

4.        Программная (тексты на языках программирования – код программы).

Пример: Требуется найти частное двух чисел.

Словесный:

1.        Задать два числа, являющиеся делимым и делителем;

2.        Проверить, равняется ли делитель нулю;

3.        Если делитель не равен нулю, то найти частное, записать его в ответ;

4.        Если делитель равен нулю, то в ответ записать "нет решения".

Словесный способ не имеет широкого распространения, так как такие описания: строго не формализуемы; страдают многословностью записей; допускают неоднозначность толкования отдельных предписаний.

Псевдокод:

 занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи. В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. Ответ при этом получает человек, который выполняет команды согласно псевдокоду.

Приведем основные управляющие структуры псевдокода в табл. 1.1.

Пример псевдокода:

алг Нахождение частного двух чисел

начало

вывод ("задайте делимое и делитель")

ввод (делимое, делитель)

если делитель ≠ 0

то частное = делимое / делитель

   вывод(частное)

иначе вывод("нет решения")

кон алг Нахождение частного двух чисел

В данном примере используется три переменные: делимое, делитель и частное. Делимое и делитель задаются исполнителем произвольными числами. Частное считается лишь в том случае, если делитель не равен нулю.

Графическая реализация алгоритма представляет собой блок-схему. Блок-схема состоит из блоков определенной формы, соединенных стрелками. Ответ при этом получает человек, который выполняет команды согласно блок-схеме.

Программная реализация алгоритма – это компьютерная программа, написанная на каком-либо алгоритмическом языке программирования, например: С++, Pascal, Basic и т.д.

Программа состоит из команд определенного языка программирования. Отметим, что одна и та же блок-схема может быть реализована на разных языках программирования. Ответ при этом получает ЭВМ, а не человек.

Различают три основных вида алгоритмов:

1.                 линейный алгоритм,

2.                 разветвляющийся алгоритм,

3.                 циклический алгоритм.

Линейный алгоритм – это алгоритм, в котором действия выполняются однократно и строго последовательно.

Самый простой пример реализации линейного алгоритма – путь из университета домой.

Словесный способ записи данного алгоритма:

1.                 выйти из университета на остановку;

2.                 подождать нужный автобус;

3.                 сесть на нужный автобус;

4.                 оплатить проезд;

5.                 выйти на требуемой остановке;

6.                 дойти до дома.

Очевидно, что данный пример относится к линейному алгоритму, т.к. все действия следуют одно за другим, без условий и повторений.

Разветвляющийся алгоритм – это алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий.

Самый простой пример реализации разветвляющегося алгоритма – если на улице идет дождь, то необходимо взять зонт, иначе не брать зонт с собой.

Приведенный выше пример псевдокода по нахождению частного двух чисел также относится к разветвляющемуся алгоритму.

Циклический алгоритм – это алгоритм, команды которого повторяются некое количество раз подряд.

Самый простой пример реализации циклического алгоритма – при чтении книги будут повторяться одни и те же действия: прочитать страницу, перелистнуть и т.д.

Блок-схема – это графическая реализация алгоритма.

Блок-схема представляет собой удобный и наглядный способ записи алгоритма.

Блок-схема состоит из функциональных блоков разной формы, связанных между собой стрелками. В каждом блоке описывается одно или несколько действий.

Любая команда алгоритма записывается в блок-схеме в виде графического элемента – блока, и дополняется словесным описанием. Блоки в блок-схемах соединяются линиями потока информации. Направление потока информации указывается стрелкой. В случае потока информации сверху вниз и слева направо стрелку ставить не обязательно. Блоки в блок-схеме имеют только один вход и один выход (за исключением логического блока – блока с условием).

Символы начала и конца программы

Схема  любого алгоритма всегда начинается терминальным символом «Начало», а заканчивается терминальным символом «Конец».

Примеры их изображения представлены на рис. 1.1.

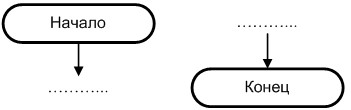
Рис. 1.1. Пример изображения терминальных символов

Данные элементы являются своеобразными точками входа и выхода из блок-схемы, поэтому символ «Начало» имеет только выходную линию, а символ «Конец» – входную.

Операторный символ

Операторный символ (или символ процесса) является базовым элементом схемы, который предназначен для отображения действий, совершаемых над данными. Текст символа может описывать как одну, так и несколько операций. Во втором случае допускается увеличение высоты символа. Пример изображения элемента представлен на рис. 1.2.

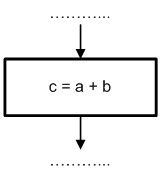
Рис. 1.2.  Пример использования операторного символа

На практике операторный символ чаще всего используется для описания процесса вычислений.

Символ ввода-вывода данных

Для обозначения операции ввода-вывода данных используется символ данных, пример изображения которого приведен на рис. 1.3.

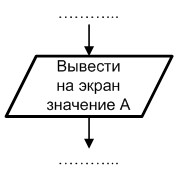
Рис. 1.3.  Пример использования символа данных

Данный элемент применяется для указания выполнения операции как ввода данных пользователем, так и чтения данных из внешнего источника. Кроме того, символ позволяет отразить процесс вывода информации на носитель любой природы (экран, ВЗУ и т. д.). При этом природа обрабатываемых данных (числовая, текстовая, графическая и т. д. информация) не имеет значения.

Комментарии

Зачастую размер символа схемы  не позволяет отразить некоторые нюансы алгоритмы. В связи с этим особо важные с содержательной точки зрения элементы могут быть сопровождены комментариями. Дополнительная информация изображается на схеме в соответствии с представленным на рис. 1.4 способом.

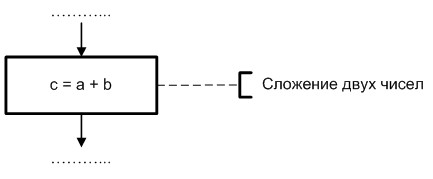
Рис. 1.4.  Пример использования комментария

Следует помнить, что текст комментария приводится на русском языке, а сам символ располагается в наиболее удобном месте схемы, не перекрывая остальные элементы схемы. Если это не нарушает общего восприятия схемы, то рекомендуется помещать пояснения в непосредственной близости от комментируемых символов.

Кроме того, допускается заключать группу символов, к которой относится комментарий, в пунктирную рамку. Пример такого изображения представлен на рис. 1.5.

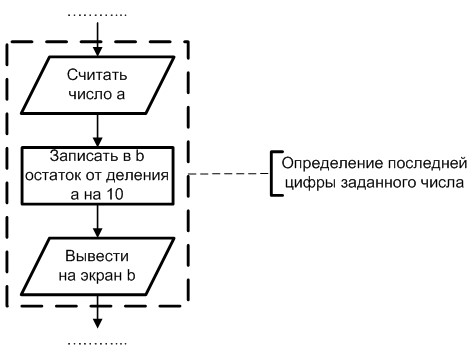
Рис. 1.5. Пример использования комментария группы символов

Общие рекомендации по оформлению схем алгоритмов

При оформлении схем алгоритмов рекомендуется придерживаться следующих правил.

1.                 Несмотря на то, что стандарт не накладывает ограничений на содержимое символов, рекомендуется описывать команды на языке, близком к естественному. Так, действие по выводу значения переменной на экран может быть записано как «writeln(X)» или «Вывести X». Второй вариант является более предпочтительным. Данная рекомендация связана с тем, что описание команд на языке, близком к конкретному языку программирования (ЯП) чревато путаницей: языки программирования имеют разную популярность и распространенность, зависящую от огромного числа факторов. Например, команда <> для подавляющего большинства неспециалистов в этом ЯП может оказаться незнакомой. Схема алгоритма – по своему назначению прежде всего универсальная структура, поэтому следует избегать ее связывания с конкретным ЯП.

2.                 Соединение элементов схемы выполняется посредством линий.

Стандартным считается направление слева направо и сверху вниз.  Для внесения ясности рекомендуется использовать стрелки, размещаемые на окончании линий.

3.                 Для всех символов за исключением условного входной считается верхняя или левая сторона, а выходной – нижняя или правая (при этом приоритет следует отдавать верхней и нижней сторонам).

4.                 По возможности следует избегать пересечения соединительных линий. В случае, когда разрыв линии позволяет оптимизировать графическое представление алгоритма, либо алгоритм является многостраничным, допускается использовать символ соединитель, изображаемый в виде круга с меткой. Соединитель в начале разрыва называется внешним соединителем, а соединитель в конце разрыва – внутренним соединителем. Пример данного действия представлен на рис. 1.6.

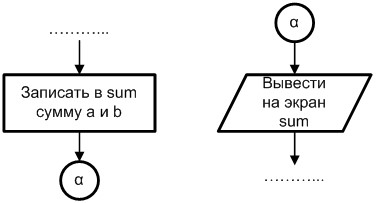
Рис. 1.6. Пример использования соединителя

5.                 При работе с соединителями следует также принимать во внимание перечисленные требования:

 необходимо обеспечивать уникальность используемой метки в пределах схемы (желательно – в пределах всего набора документации);

 допускается использовать несколько внешних соединителей с одной меткой, однако метки всех внутренних соединителей должны быть попарно различны;

 соединители рекомендуются к применению при переносе части схемы на другую страницу (при этом в комментарии следует указывать номер следующей страницы).

6.                 При печати допускается изображение схем как в книжной, так и в альбомной ориентациях.

7.                 Если размер символа не позволяет включить в него минимум текста для описания его смысловой нагрузки, то допускается изложение части содержимого (или всего текста) в символе комментария.

8.                 Если это необходимо, допускается присваивание символу уникального идентификатора, который размещается слева и сверху от соответствующего блока. Данный идентификатор может быть использован в сопроводительном тексте для явной ссылки на символ. Пример изображения идентификатора представлен на рис. 1.7.

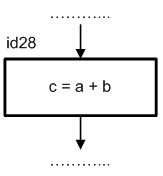
Рис. 1.7.  Пример использования идентификатора

Типовые ошибки, как правило, связаны с нарушением следующих правил:

 ширина всех блоков схемы должна быть одинаковой;

           при      соединении     блоков     следует     использовать     только

вертикальные и горизонтальные линии потоков;

 горизонтальные потоки, имеющие направление справа налево, и вертикальные потоки, имеющие направление снизу вверх, должны быть обязательно помечены стрелками;

 линии потоков должны быть параллельны линиям внешней рамки или границам листа;

 текст символов и комментариев должен записываться слева направо и сверху вниз независимо от направления потоков данных или управления;

 как правило, каждый символ имеет один вход и один выход, исключение составляют:  терминальные символы (у операции «начало» нет входа, у операции

«конец» нет выхода); символы решения (один вход и несколько выходов).

Условный оператор

Подавляющее большинство алгоритмов имеет структуру, отличную от линейной. На практике часто возникает необходимость проведения анализа исходных данных или промежуточных результатов вычислений с целью определения дальнейшего порядка выполнения вычислительного процесса. Алгоритмы, в которых в зависимости от выполнения некоторого логического условия происходит разветвление вычислений по одному из нескольких возможных направлений, называют разветвляющимися. Подобные алгоритмы предусматривают выбор одного из альтернативных путей продолжения вычислений. Каждое возможное направление вычислений называется ветвью. Логическое условие называют простым, если разветвляющийся процесс имеет две ветви, и сложным, если процесс разветвляется на три и более ветви. Для выбора дальнейшей цепочки операций предназначен символ решения. Пример изображения данного элемента представлен на рис. 2.1.

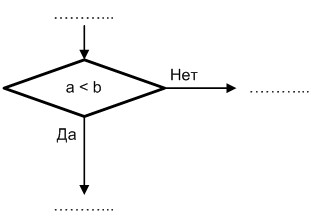
Рис. 2.1.  Пример изображения символа решения

Приведенный выше символ эквивалентен характерному практически для всех языков программирования условному оператору.

При использовании символа необходимо придерживаться следующих правил.

1.                 Символ может иметь один и только один вход и ряд взаимоисключающих (альтернативных) выходов.

2.                 Текст символа должен содержать описание какого-либо логического условия или действия, предполагающего сравнение элемента с набором допустимых значений. В случае задания  логического условия допускается постановка знака вопроса (?).  Размещение описания операций внутри символа не допускается.

3.                 Входным считается верхний угол блока, а выходными – остальные.

4.                 Выходящие ветви должны сопровождаться текстом, однозначно определяющим выполняемые в дальнейшем операции

(выбранный путь). В случае, когда текст символа содержит условие, разрешается использовать пары идентификаторов вида «Да» – «Нет», «1»– «0», «Истина» – «Ложь», «True» – «False» и т. д.

Как было сказано ранее, символ решения может иметь более двух выходов. В этом случае допускается наличие как нескольких выходящих ветвей, так и одной ветви, разделяющейся в дальнейшем. Все прочие рекомендации по оформлению символа остаются актуальными. Пример изображения символа решения с группой выходов представлен на рис. 2.2.

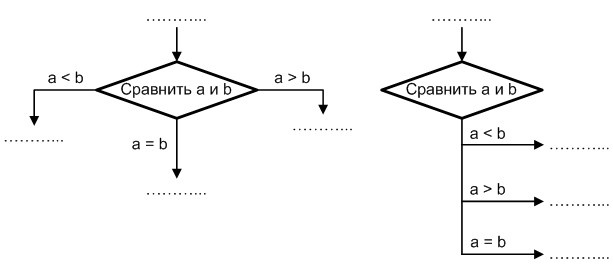
Рис. 2.2. Пример изображения символа решения с группой выходов

Следует обратить внимание, на тот факт, что при наличии ровно двух альтернатив рекомендуется в целях внесения большей ясности избегать варианта оформления с единственным разделяющимся выходом.

Организация циклических процессов

Часто при решении задач приходится многократно выполнять одни и те же операции для различных значений входящих величин. Такие многократно повторяемые участки вычислительного процесса называются алгоритмами циклической структуры, или циклами. Использование циклов позволяет существенно сократить объем схемы алгоритма и длину соответствующей ей программы. Группы повторяющихся вычислений называют тело цикла. Специально изменяемый по заданному закону параметр, входящий в тело цикла, называется переменной цикла. Переменная цикла используется для подготовки очередного повторения цикла и отслеживания условий его окончания.

В качестве переменной цикла используют любые переменные, индексы массивов, аргументы вычисляемых функций и т. д.

Для правильной организации цикла необходимо:

 задать перед циклом начальное значение переменной, изменяющейся в цикле;

 выполнить тело цикла;

 изменить переменную перед каждым новым повторением цикла;  проверить условие окончания или повторения цикла.

Циклические алгоритмы, в которых число повторений заранее известно из исходных данных или определено в ходе решения задачи, называют детерминированными, если число повторений тела цикла заранее неизвестно, а зависит от значений параметров, участвующих в вычислениях цикл называют итерационным.

Для отображения циклических процессов используется символ, состоящий из двух частей, определяющий начало и конец цикла (рис. 2.3). Обе части символа имеют один и тот же идентификатор. Условия для инициализации, завершения могут помещаться внутри символа в начале или в конце. В зависимости от расположения операции проверки условия циклы могут быть организованы как циклы с предусловием или с постусловием.

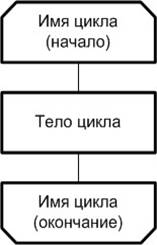
Рис. 2.3. Пример изображения символа цикла

Циклы с предусловием

Если в цикле с предусловием входящие в тело цикла команды могут не выполняться ни разу (если начальное значение параметра цикла удовлетворяет условию выхода из цикла, рис. 2.4)

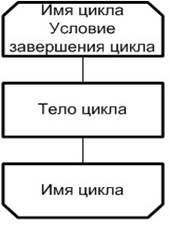
Рис. 2.4. Пример изображения цикла с предусловием

Циклы с постусловием

В цикле с постусловием – выполняются как минимум один раз (даже если начальное значение параметра цикла удовлетворяет условию выхода из него, рис. 2.5).

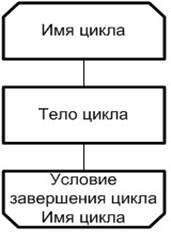
Рис. 2.5. Пример изображения цикла с постусловием

Операция по модификации переменой цикла может быть определена как в теле цикла, так и в символе конца. Недопустима модификация переменной цикла в символе начала цикла.

Скачано с www.znanio.ru